



初中数学人教版八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.3 正方形精品同步训练题
展开2022-2023学年人教版数学八年级下册同步重难点精讲精练培优讲义
18.2.3 正方形
1.理解正方形的概念,了解平行四边形、矩形及菱形与正方形的概念之间的从属关系;
2.掌握正方形的性质及判定方法.
知识点01:正方形的定义
四条边都相等,四个角都是直角的四边形叫做正方形.
要点诠释:既是矩形又是菱形的四边形是正方形,它是特殊的菱形,又是特殊的矩形,更为特殊的平行四边形,正方形是有一组邻边相等的矩形,还是有一个角是直角的菱形.
知识点02:正方形的性质
正方形具有四边形、平行四边形、矩形、菱形的一切性质.
1.边——四边相等、邻边垂直、对边平行;
2.角——四个角都是直角;
3.对角线——①相等,②互相垂直平分,③每条对角线平分一组对角;
4.是轴对称图形,有4条对称轴;又是中心对称图形,两条对角线的交点是对称中心.
要点诠释:正方形具有平行四边形、矩形、菱形的一切性质,其对角线将正方形分为四个等腰直角三角形.
知识点03:正方形的判定
正方形的判定除定义外,判定思路有两条:或先证四边形是菱形,再证明它有一个角是直角或对角线相等(即矩形);或先证四边形是矩形,再证明它有一组邻边相等或对角线互相垂直(即菱形).
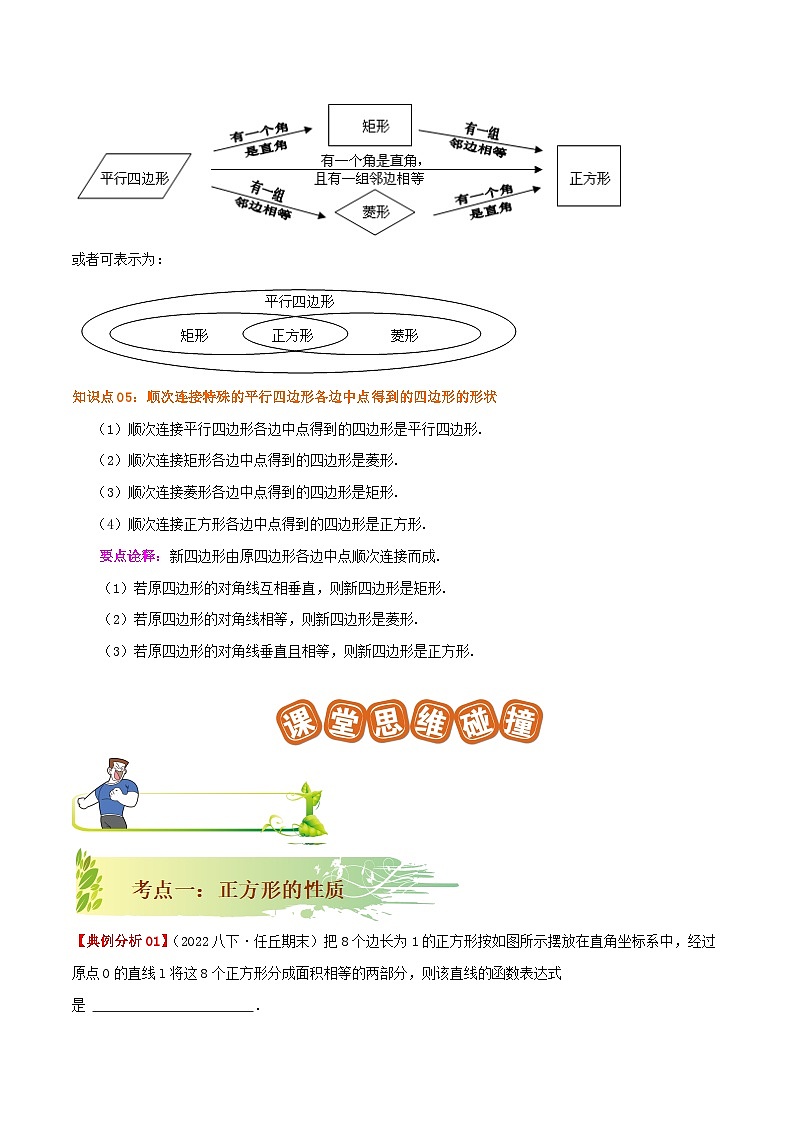
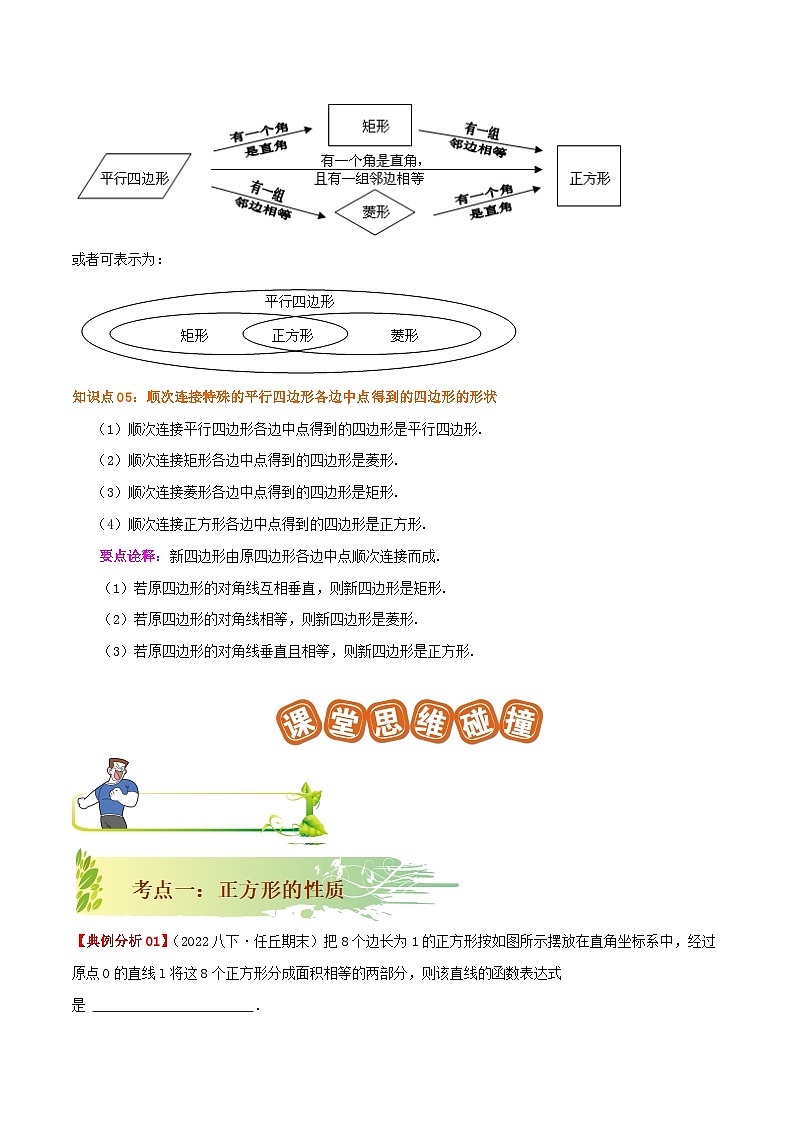
知识点04:特殊平行四边形之间的关系
或者可表示为:
知识点05:顺次连接特殊的平行四边形各边中点得到的四边形的形状
(1)顺次连接平行四边形各边中点得到的四边形是平行四边形.
(2)顺次连接矩形各边中点得到的四边形是菱形.
(3)顺次连接菱形各边中点得到的四边形是矩形.
(4)顺次连接正方形各边中点得到的四边形是正方形.
要点诠释:新四边形由原四边形各边中点顺次连接而成.
(1)若原四边形的对角线互相垂直,则新四边形是矩形.
(2)若原四边形的对角线相等,则新四边形是菱形.
(3)若原四边形的对角线垂直且相等,则新四边形是正方形.
【典例分析01】(2022八下·任丘期末)把8个边长为1的正方形按如图所示摆放在直角坐标系中,经过原点O的直线l将这8个正方形分成面积相等的两部分,则该直线的函数表达式是 .
【答案】y=x或y=0.9x
【规范解答】解:如图,过A作AB⊥y轴,垂足为点B,则OB=3,
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴S△AOB=4+1=5,
∵OB=3,
∴AB•3=5,
解得:AB=,
∴A点坐标为(,3),
设直线方程为y=kx,
则3=k,
∴k=,
∴直线l解析式为y=x.
故答案为:y=x.
【思路引导】过A作AB⊥y轴,垂足为点B,则OB=3,由于经过原点的一条直线l将这八个正方形分成面积相等的两部分,可得S△AOB=5=×AB·OB,据此求出AB=,即得A(,3),利用待定系数法求出直线l解析式即可.
【典例分析02】(2022八下·范县期末)如图,已知正方形的边长为4,点P是对角线上一点,于点E,于点F,连接.给出下列结论:
①;②四边形的周长为8;
③;④;⑤的最小值为.
其中正确结论的序号为( )
A.①②③⑤ B.②③④ C.②③④⑤ D.②③⑤
【答案】C
【规范解答】①∵PE⊥BC于点E,PF⊥CD于点F,CD⊥BC,
∴PF∥BC,
∴∠DPF=∠DBC,
∵四边形ABCD是正方形
∴∠DBC=45°
∴∠DPF=∠DBC=45°,
∴∠PDF=∠DPF=45°,
∴PF=EC=DF,
在Rt△DPF中,DP2=DF2+PF2=DF2+DF2=2DF2,
∴PD=DF
∴PD=.
故①不符合题意;
②∵PE⊥BC,PF⊥CD,∠BCD=90°,
∴四边形PECF为矩形,
又∵PE=CE
∴四边形PECF的周长=2CE+2PE=2CE+2BE=2BC=8,
故②符合题意;
③如图1
延长FP交AB于G,延长AP交EF于H,
在正方形ABCD中,
∴CD∥AB
又∵PF⊥于CD
∴∠AGP=90°;
由②知四边形PECF是矩形,
∴∠EPF=90°
∴∠AGP=∠EPF;
由①知PF=DF,
又∵AG=DF
∴AG=PF
∴四边形BGPE是正方形,
∴PG=PE
∴△AGP≌△FPE
∴∠BAP=∠PFE
又∵∠APG=∠FPH,∠BAP与∠APG互余
∴∠FPH与∠PFE互余
∴∠PHF=90°即AP⊥EF
故③符合题意;
④由③知,△AGP≌△FPE
∴AP=EF
故④符合题意;
⑤当时,AP最小;
∴EF的最小值为.故⑤符合题意.
综上:②③④⑤符合题意.
故答案为:C.
【思路引导】结合图形,利用正方形的性质,勾股定理等计算求解即可。
【随堂演练01】(2022八下·抚远期末)如图,正方形的边长为1,,是对角线,将绕点顺时针旋转45°得到,交于点,连接交于点,连接,则下列结论:①四边形是菱形;②;③;④.其中结论正确的是( )
A.①②③ B.①②④ C.②③④ D.①③④
【答案】A
【规范解答】解:证明:∵四边形ABCD是正方形,
∴AD=DC=BC=AB,∠DAB=∠ADC=∠DCB=∠ABC=90°,∠ADB=∠BDC=∠CAD=∠CAB=45°,
∵△DHG是由△DBC旋转得到,
∴DG=DC=AD,∠DGE=∠DCB=∠DAE=90°,
在Rt△ADE和Rt△GDE中,
,
∴Rt△AED≌Rt△GED(HL),故②符合题意;
∴∠ADE=∠EDG=22.5°,AE=EG,
∴∠AED=∠AFE=67.5°,
∴AE=AF=EG,
又∵∠H=∠DBC=∠DAC=45°,
∴GH∥AC,
∴四边形AEGF是菱形,故①符合题意;
∵∠DFG=∠GFC+∠DFC=∠BAC+∠DAC+∠ADF=112.5°,故③符合题意;
∵AE=FG=EG=BG,BE=HE,
∴BE>AE,
∴AE<,
∴CB+FG<1.5,故④不符合题意.
故答案为:A.
【思路引导】根据正方形的性质,得到四边相等,四个角90°,对角线平分对角,Rt△AED≌Rt△GED(HL),证得②;Rt△AED≌Rt△GED(HL),求得∠ADE=∠EDG=22.5°,AE=EG,根据菱形判定定理证得四边形AEGF是菱形;通过角的等量替换即可得到∠DFG=112.5°;通过等量替换得到AE<,得不到④.
【随堂演练02】(2022八下·涿州期末)如图,以正方形ABCD的中心为原点建立平面直角坐标系,点A的坐标为(2,2),则点D的坐标为( )
A.(2,2) B.(﹣2,2)
C.(﹣2,﹣2) D.(2,﹣2)
【答案】B
【规范解答】解:如图所示:
∵以正方形ABCD的中心O为原点建立坐标系,点A的坐标为(2,2),点D与点A关于y轴对称,
∴点D的坐标分别为:(﹣2,2).
故答案为:B.
【思路引导】由题意可知点D与点A关于y轴对称,继而求解.
【典例分析03】(2022八下·涿州期末)如图,已知矩形ABCD中,添加下列条件能使矩形ABCD成为正方形的是( )
A.AC=BD B.AB⊥BC C.AD=BC D.AC⊥BD
【答案】D
【规范解答】解:∵四边形ABCD是矩形,
∴当AC⊥BD或当AD=AB时,四边形ABCD是正方形;
故答案为:D
【思路引导】对角线相等的矩形是正方形,邻边相等的矩形是正方形,据此逐一判断即可.
【典例分析04】(2022八下·无为期末)下列说法正确的是( )
A.对角线互相垂直的四边形是菱形
B.四条边都相等的四边形是正方形
C.一组对边平行,另一组对边相等的四边形是平行四边形
D.四个角相等的四边形是矩形
【答案】D
【规范解答】解:A:对角线互相垂直且平分的的四边形是菱形,故A不符合题意
B:四条边都相等且有一个角为直角的平形四边形是正方形,故B不符合题意
C:一组对边平行且相等的四边形是平行四边形,故C不符合题意
D:四个角相等的四边形是矩形,符合题意
故答案为:D
【思路引导】利用菱形、正方形、平行四边形和矩形的判定方法逐项判断即可。
【随堂演练03】(2022八下·潮安期末)如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
【答案】(1)证明:∵点D、E分别是边BC、AC的中点,∴DE∥AB,
∵AF∥BC,∴四边形ABDF是平行四边形,∴AF=BD,则AF=DC=AD,
∵AF∥BC,∴四边形ADCF是平行四边形;
(2)解:当△ABC是等腰直角三角形时,四边形ADCF是正方形,
理由:∵四边形ADCF是正方形,∴∠ADC=90°,AC=DF,AF=DC.
∵点D,E分别是边BC,AC的中点,AB=2DE,∴AB=DF,所以AB=AC.
∴四边形ABDF是平行四边形,∴AF=BD,∴BD=CD=AD,
∴∠BAC=90°,
∴△ABC是等腰直角三角形.
【思路引导】(1)利用一组对边平行且相等的四边形是平行四边形的判定方法求解即可;
(2)先证明四边形ABDF是平行四边形,可得BD=CD=AD,求出∠BAC=90°,即可得到△ABC是等腰直角三角形。
【随堂演练04】(2022八下·滨城期末)如图,已知四边形,下列说法中正确的是( )
A.若,,则四边形是矩形
B.若,,则四边形是菱形
C.若,则四边形是正方形
D.若,,则四边形是平行四边形
【答案】D
【规范解答】解:A.由AC⊥BD,AC=BD,不能判定四边形ABCD是矩形,
故A选项不符合题意;
B.∵AC⊥BD,AB=AD,CB=CD,不能判定四边形ABCD是菱形,
故B选项不符合题意;
C.∵AB=BC=CD=AD,
∴四边形ABCD是菱形,不一定是正方形,
故C选项不符合题意;
D.∵AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
故D选项符合题意,
故答案为:D.
【思路引导】利用矩形,菱形,正方形和平行四边形的判定方法对每个选项一一判断即可。
【典例分析05】(2022八下·顺平期末)如图,在中,点D,E,F分别是的中点,连接.
(1)试猜想四边形的形状,并说明理由.
(2)若,试判断线段与的关系,并说明理由.
【答案】(1)解:猜想四边形是平行四边形,理由如下,∵点D,E,F分别是的中点∴是的中位线∴,∴四边形是平行四边形
(2)解:,理由如下,∵,点E,F分别是的中点,∴∵四边形是平行四边形,∴四边形为菱形,又∵∴为正方形∴,
【思路引导】(1)猜想四边形是平行四边形,理由:先确定是的中位线,根据三角形中位定理可得,,根据两组对边分别平行的四边形是平行四边形即证;
(2),理由:根据线段的中点及AC=BC,可推出EC=FC,由(1)知四边形是平行四边形,从而可证四边形为菱形,结合∠C=90°,可证四边形为正方形,根据正方形的性质即得结论.
【典例分析06】(2022八下·剑阁期末)如图,点P是正方形 的对角线 上一点, ,垂足分别为点E,F,连接 ,给出下列四个结论:① ;② ;③ ;④ 一定是等腰三角形.其中正确的结论序号是 .
【答案】①②③
【规范解答】解:
延长PF交AB于点G,
∵四边形ABCD是正方形,
∴AB∥CD,AB=BC=CD=AD,
∵PF⊥CD,AB∥CD,
∴PG⊥AB,即∠PGB=90°,
∵PE⊥BC,PF⊥CD,
∴四边形GBEP为正方形,四边形PFCE为矩形,
∴GB=BE=EP=GP,PF=CE,∠EPF=90°,
∴AB-BG=CD-BE,即AG=CE=PF,
在△AGP和△FPE中,
AG=FP∠AGP=∠FPEPG=PE,
∴△AGP≌△FPE(SAS),
∴AP=EF,∠PFE=∠BAP,
故①②正确;
∵BC=CD,BE=CF,
∴CE=PF=DF,
在Rt△PDF中,由勾股定理得PD=,
故③正确;
∵P在BD上,
∴当AP=DP、AP=AD、PD=DA时,△APD才是等腰三角形,
∴△APD是等腰三角形共有3种情况,故④错误,
故答案为:①②③.
【思路引导】延长PF交AB于点G,由正方形ABCD和PE⊥BC,PF⊥CD可证出四边形GBEP为正方形,四边形PFCE为矩形,然后用“边角边”证△AGP≌△FPE,利用全等三角形的性质(全等三角形对应边相等,对应角相等)即可证①②正确;由勾股定理可以得出PD=,可证③正确;点P在BD上要使△APD一定是等腰三角形,只有当AP=DP、AP=AD、PD=DA时才成立,可判断④错误.
【随堂演练05】(2022八下·灌阳期末)如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是 .
【答案】
【规范解答】解:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG.
在△AEH、△BFE、△CGF和△DHG中,
AE=BF=CG=DH∠A=∠B=∠C=∠DAH=BE=CF=DG
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形,
∵AB=BC=CD=DA=8,AE=BF=CG=DH=5,
∴EH=FE=GF=GH=
所以正方形EFGH的面积
故答案为:.
【思路引导】根据正方形的性质可得∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,根据线段的和差关系可得AH=BE=CF=DG,证明△AEH≌△BFE≌△CGF≌△DHG,得到EH=FE=GF=GH,∠AEH=∠BFE,推出四边形EFGH是菱形,易得∠HEF=90°,则四边形EFGH是正方形,然后利用勾股定理计算即可.
【随堂演练06】(2022八下·邻水期末)如图,正方形ABCD和正方形EFCG的边长分别为3,1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为 .
【答案】
【规范解答】解:延长GE交AB于点O,作PH⊥OE于点H,
∵正方形ABCD,正方形EFCG,
∴EF=1,AB=3,四边形EFBO,ODG是矩形,
∴EF=OB=1
∴AO=BF=AB-OB=3-1=2;
∵PH∥AB,
∵P是AE的中点,
∴PH是△AOE的中位线,
∴PH=OA=×2=1,
∵在Rt△AOE中,∠OAE=45°,
∴△AOE是等腰直角三角形,
∴OA=OE=2,
同理可知HE=PH=1.
∴HG=HE+EG=1+1=2.
在Rt△PHG中,
.
故答案为:.
【思路引导】延长GE交AB于点O,作PH⊥OE于点H,利用正方形的性质和判定,可证得EF=OB=1,可求出AO的长;再利用三角形的中位线定理可求出PH的长;再利用等腰直角三角形的判定和性质可得到OA=OE=2,同时可求出HG的长;然后利用勾股定理求出PG的长.
一、选择题
1.(2022秋·江苏盐城·八年级校考期中)用两块完全重合的等腰直角三角形纸片拼下列图形:①平行四边形(不包括菱形、矩形、正方形);②矩形(不包括正方形);③正方形;④等腰直角三角形;⑤等边三角形.一定能拼接成的图形是( )
A.①②③ B.②③④ C.①③④ D.①③④⑤
【答案】C
【思路引导】本题是开放题,可以针对各种特殊的等腰三角形的组合方法,得出不同的图形.
【规范解答】解:①平行四边形
③正方形
④等腰直角三角形
故选:C.
【考察注意点】本题考查全等三角形、矩形、平行四边形、正方形、等腰直角三角形、等边三角形,解答此类题的关键是要突破思维定势的障碍,运用发散思维,多方思考,探究问题在不同条件下的不同结论.
2.(2023·全国·八年级专题练习)如图,在四边形中,对角线相交于点O.下列说法不正确的的是( )
A.如果,那么可得矩形;
B.如果是菱形,那么可得;
C.如果,那么可得正方形;
D.如果,那么可得矩形;
【答案】C
【思路引导】根据矩形,菱形,正方形的判定方法,逐项判断即可求解.
【规范解答】解:∵,
∴四边形是平行四边形,,
∴四边形是矩形,故A选项正确,不符合题意;
∵四边形是菱形,
∴,故B选项正确,不符合题意;
若四边形是平行四边形,,则可得正方形,故C选项错误,符合题意;
∵,
∴四边形是矩形,故D选项正确,不符合题意;
故选:C
【考察注意点】本题主要考查了矩形,菱形,正方形的判定,熟练掌握矩形,菱形,正方形的判定定理是解题的关键.
3.(2022秋·浙江宁波·八年级统考期末)如图,正方形的面积为a,E,F,G,H分别是它的四条边上的点,且,四边形面积为b,它的对角线所在直线与正方形边所在直线分别相交,组成的阴影部分面积记为c.若,则的值为( )
A. B. C. D.
【答案】C
【思路引导】设,,根据正方形的性质及面积法可得答案.
【规范解答】解:设,,
∵四边形是正方形,
∴,
∴,
∵,
∴,
∴,
∴,
∴垂直平分,
∴,
∵四边形是正方形,
∴,,
∴,
∴,
∴,
∴,
∴,
故选:C.
【考察注意点】此题考查了正方形的性质,熟练掌握正方形的性质是解题的关键.
4.(2021春·重庆沙坪坝·八年级重庆市第七中学校校考期中)如图,正方形中,点是对角线上的一点,且,连接,,则的度数为( )
A. B. C. D.
【答案】B
【思路引导】根据正方形的性质,得到,,进而得到,又因为,得到,推出,即可得到答案.
【规范解答】解:四边形是正方形,
,,
,
,
,
,
故选B.
【考察注意点】本题考查了正方形的性质,三角形内角和定理,等腰三角形的判定和性质,熟练掌握正方形对角线平分每一组对角是解题关键.
5.(2021春·江苏苏州·八年级校考期中)如图,正方形的边长为3,点M在延长线上,,作交延长线于点N,则的长为( )
A.3 B.4 C.5 D.6
【答案】C
【思路引导】如图所示,在上取一点F,使得,连接,先证明得到,进而可以证明得到,设,则,,在中利用勾股定理求解即可.
【规范解答】解:如下图所示,在上取一点F,使得,连接,
四边形是正方形,
,
,
,
,
又,
,
又,
,
,
设,
,
,
,
在中,,
,
解得,
,
故选:C.
【考察注意点】本题考查了正方形的性质,全等三角形的性质与判定,勾股定理,正确作出辅助线构造全等三角形是解题的关键.
6.(2022秋·浙江绍兴·八年级校考期末)如图,在直线l上有正方形a,b,c,若a,c的面积分别为4和16,则b的面积为( )
A.24 B.20 C.12 D.22
【答案】B
【思路引导】利用正方形性质证明,再利用勾股定理得,即可解题.
【规范解答】解:∵a、b、c都是正方形,
∴,,
∵,
即,,,
∴,
∴,,
在中,由勾股定理得:,
即,故B正确.
故选:B.
【考察注意点】此题主要考查对全等三角形和勾股定理的综合运用,中等难度,结合图形求解,对图形的理解能力要比较强,证明全等是解题关键.
7.(2021春·江苏苏州·八年级校考期中)如图,正方形中,对角线交于点,折叠正方形纸片,使落在上,点恰好与上的点重合,展开后折痕分别交于点,连接,给出下列结论,其中正确的个数有( ).
①; ②
③四边形是菱形; ④.
A.1个 B.2个 C.3个 D.4个
【答案】B
【思路引导】①由四边形是正方形,可得,又由折叠的性质,可求得的度数,从而求得;②证得,由即可得;③由折叠的性质与平行线的性质,易得是等腰三角形,由、即可得证;④设,先求得,从而知.
【规范解答】解:四边形是正方形,
,
由折叠的性质可得:,
,故①错误.
由折叠的性质可得:,,
在和中,
,
,
,
在中,,
,故②错误;
,
,
又、,
,
四边形是菱形,故③正确;
设,
四边形是菱形,且,
,
,
又,
,
,
,,
,即,
,故④正确;
故选:B.
【考察注意点】此题考查的是正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识.此题综合性较强,难度较大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.
二、填空题
8.(2023·全国·八年级专题练习)如图,将正方形沿对折,使点落在对角线上的处,连接,则 _________.
【答案】67.5
【思路引导】根据正方形的性质求出,再根据折叠的性质得,进而根据等腰三角形的性质得出答案.
【规范解答】∵四边形为正方形,
∴,,平分,
∴,
根据折叠可知,,
∴,
∴.
故答案为:67.5.
【考察注意点】本题主要考查了正方形的性质,折叠的性质,等腰三角形的性质等,判定等腰三角形是解题的关键.
9.(2023秋·吉林长春·八年级长春外国语学校校考期末)如图,在正方形中,点为边上一点,与交于点.若,则的大小为______度.
【答案】65
【思路引导】由三角形的外角性质可知:要求,只要求,由正方形的轴对称性质可知:,即可求出.
【规范解答】解:四边形是正方形,具有关于对角线所在直线对称的对称性,
,,,
又是的外角,
,
故答案为:65.
【考察注意点】本题综合考查正方形的对称性质和三角形外角性质,解题关键是利用正方形的对称性快速得出结论.
10.(2022秋·黑龙江大庆·八年级校考阶段练习)如图,在边长为的正方形中,、分别为与的中点,一个三角形沿竖直方向向上平移,在运动的过程中,点A恒在直线上,当点A运动到线段的中点时,点,恰与,两边的中点重合,设点A到的距离为,三角形与正方形的公共部分的面积为,则当时,的值为______.
【答案】
【思路引导】分两种情形:如图中,当过A在正方形内部时,连接交于,连接,设交于,交于;如图中,当点A在正方形外部时,分别求解即可解决问题.
【规范解答】解:如图中,当过A在正方形内部时,连接交于,连接,设交于,交于.
由题意,是等腰直角三角形,,,
,
,
,
,
;
如图中,当点在正方形外部时,
由题意,重叠部分是六边形,,
,
解得:,
,
综上所述,满足条件的的值为,
故答案为:.
【考察注意点】本题考查正方形的性质,平移变换,多边形的面积等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题.
11.(2022秋·吉林长春·八年级校考期末)如图,在正方形中,,点F在边上运动(不包含两个端点),点E是边的中点,连接,,.当为等腰三角形,为底边时,的长为___________.
【答案】
【思路引导】根据正方形的性质,得出,,设,则,根据勾股定理得出,求出x的值即可.
【规范解答】解:∵四边形为正方形,
∴,,
∵点E是边的中点,
∴,
设,则,
根据勾股定理得:,
,
∵为等腰三角形,为底边,
∴,
∴,
解得:,
即的长为.
故答案为:.
【考察注意点】本题主要考查了等腰三角形的定义,勾股定理,正方形的性质,解题的关键是设,根据勾股定理列出关于x的方程.
12.(2022春·江苏苏州·八年级校考阶段练习)已知一个对角线长分别为和的菱形,顺次连接它的四边中点得到的四边形的面积是______.
【答案】##48平方厘米
【思路引导】根据顺次连接这个菱形各边中点所得的四边形是矩形,且矩形的边长分别是菱形对角线的一半,问题得解.
【规范解答】解:、、、分别为各边中点,
,,
,,
,
,
四边形是矩形,
,,
矩形的面积,
故答案为:.
【考察注意点】本题考查菱形的性质,菱形的四边相等,对角线互相垂直,连接菱形各边的中点得到矩形,且矩形的边长是菱形对角线的一半.
13.(2021春·江苏苏州·八年级校考期中)如图,矩形中,,,动点P从点A出发,以每秒个单位长度的速度沿线段运动,动点Q从点D出发,以每秒2个单位长度的速度沿折线段运动,已知P、Q同时开始移动,当动点P到达D点时,P、Q同时停止运动.设运动时间为t秒.若线段的中点为M,在整个运动过程中,写出点M运动路径的长度为___________.
【答案】
【思路引导】分类讨论点Q在线段上和点Q在线段上时点M的轨迹,计算出轨迹即可.
【规范解答】解:①如图,点Q在线段上,过点O作于点K,过点Q作于点H,
矩形,
,
,
,
,
,
,
,
点M在线段上,当点P到达K点时,点Q到达O点,此时点M在点E处,
这时段点M的运动轨迹为;
②如图,点Q在线段上,取的中点,的中点M,连接,则点M的运动轨迹是线段,
在中,.
在整个过程中,点M的运动轨迹的长度为.
故答案为:.
【考察注意点】本题考查了矩形的性质,等腰三角形的性质,中位线的性质,勾股定理,解决本题的关键是找到点Q和点P的轨迹之间的关系.
14.(2021春·重庆沙坪坝·八年级重庆市第七中学校校考期中)如图,在正方形中,是对角线上一点,过点作,交于点,,,则___________.
【答案】
【思路引导】作出如图的辅助线,证明,推出,,再证明,可推出为等腰直角三角形,求得长,设,由勾股定理建立方程即可求的长.
【规范解答】解:连接、,过点E作于点M,如图所示,
∵四边形为正方形,
∴,,,,
∴,,
∴,,
∵,
∴,
∴,
∵,
∴
∴,
∴,
∴,
∴为等腰直角三角形,
∵,,
∴,
∵,即,
∴,
设,
在中,,
∴,解得,
∴.
故答案为:.
【考察注意点】本题考查了正方形性质、勾股定理、等腰直角三角形的判定与性质;熟练掌握正方形的性质,证明是解决问题的关键.
三、解答题
15.(2021春·吉林长春·八年级校考期中)如图,在四边形中,,且,,,动点、分别从、同时出发,点以每秒1个单位的速度由向运动,点以每秒2个单位的速度由向运动,其中一动点到达端点时,另一动点随之停止运动,设运动时间为(秒).
(1)用含的代数式表示:
______;______;______;______.
(2)、与四边形的两个顶点所形成的四边形是平行四边形时,求值.
【答案】(1),,,
(2)的值为秒或秒
【思路引导】(1)根据速度时间路程分别表示相应的长度即可;
(2)分两种情况进行讨论:①当四边形为平行四边形时;②当四边形为平行四边形时;结合平行四边形的性质列方程求解即可.
【规范解答】(1)解:根据题意得:,,,,
故答案为:,,,;
(2)①当四边形为平行四边形时,
由可得:,
解得:;
②当四边形为平行四边形时,
由可得:,
解得:,
综上所述:、与四边形的两个顶点所形成的四边形是平行四边形时,的值为秒或秒.
【考察注意点】本题考查了四边形动点问题,熟练掌握平行四边形的性质,利用平行四边形的性质列方程求解是本题的关键.
16.(2022秋·吉林白城·八年级校考阶段练习)如图,已知正方形中,边长为,点在边上,.点在线段上以/秒的速度由点向点运动,同时,点在线段上以厘米/秒的速度由点向点运动,设运动的时间为秒.
(1) , .(用含的代数式表示)
(2)若以、、为顶点的三角形和以、、为顶点的三角形全等,求的值.
【答案】(1);
(2)或
【思路引导】(1)点在线段上以/秒的速度由点向点运动,,由此即可求解;
(2)分类讨论,若,,;若,
,,由此即可求解.
【规范解答】(1)解:∵点在线段上以/秒的速度由点向点运动,
∴,,
故答案为:;.
(2)解:①若,
则,即,则,
∴;
②若,
则,,则,
∴,解得:.
【考察注意点】本题主要考查正方形的性质,动点问题,全等三角形的性质,掌握动点与正方形的性质,全等三角形的性质是解题的关键.
17.(2022秋·山东东营·八年级东营市东营区实验中学校考期末)如图,在四边形中,,,,,,点P从点A出发以的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为.
(1)从运动开始,当t取何值时,四边形是平行四边形?
(2)在运动过程中,是否存在以为腰的等腰三角形?若存在,求出时间t的值;若不存在,说明理由.
【答案】(1)
(2)
【思路引导】(1)首先判定当时,四边形是平行四边形,然后利用其性质,构建方程,即可得解;
(2)根据题意分和两种情况讨论,分别根据等腰三角形的性质求解即可.
【规范解答】(1)当时,四边形PDCQ是平行四边形,
此时,
∴,
∴,
∴当时,四边形是平行四边形.
(2)如图所示,作交于点E,
∵
∴
∴四边形是矩形
∴,
∴
∴在中,,
∴如图所示,当时,
∴;
当时,
∵
∴
∴,
∵,点P从点A出发以的速度沿A→D→C运动,
∴当点P 倒点C停止运动时,,
∵当点P到达点C时,点Q也停止运动,
∴点Q运动的时间最多为11秒,
∵,
∴应舍去,
综上所述,当时,是以为腰的等腰三角形.
【考察注意点】此题主要考查动点问题,平行四边形的判定,一元一次方程,等腰三角形的性质等知识,解题的关键是根据题意列出方程求解.
18.(2023春·江苏·八年级专题练习)如图1,在正方形中,点E为上一点,连接,把沿折叠得到,延长交于G,连接.
(1)求证:.
(2)如图2,E为的中点,连接.
①求证:;②若正方形边长为6,求线段的长.
【答案】(1)证明见解析;
(2)①证明见解析,②线段的长为2
【思路引导】(1)由正方形的性质可得.,由折叠的性质得出,,,再求出,,然后由“”证明,由全等三角形对应角相等得出,得出即可;
(2)①由折叠的性质和线段中点的定义可得,,再由三角形的外角性质得出,然后利用同位角相等,两直线平行证明即可;
②设,表示出、,根据点是的中点求出、,从而得到的长度,再利用勾股定理列出方程求解即可;
【规范解答】(1)证明:如图1:∵四边形是正方形,
.,
沿折叠得到,
,,,
,,
在和中,
,
,
,
,
,
,
;
(2)证明:如图2所示:
沿折叠得到,为的中点,
,,
,
,
,
,
即,
;
②解:设,则,,
正方形边长为6,为的中点,
,
,
在中,根据勾股定理得:,
解得:,
即线段的长为2.
【考察注意点】本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理、翻折变换的性质;熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键.
19.(2022秋·山东聊城·八年级校考期末)已知正方形中,,.动点以每秒2个单位速度从点出发沿线段方向运动,动点同时以每秒8个单位速度从点出发沿正方形的边方向顺时针作折线运动,当点与点相遇时停止运动,设点的运动时间为.
(1)当运动时间为__ 秒时,点P与点Q相遇;
(2)当时,求线段的长度;
(3)连接,当和全等时,求的值.
【答案】(1)
(2)
(3)t为或
【思路引导】(1)先判断出点,相遇时,必在正方形的边上,利用运动路程之和为正方形的正常建立方程即可;
(2)先判断出四边形是平行四边形,得出,进而表示出,,用建立方程求解即可;
(3)分点在正方形的边,,,上,建立方程求解即可得出结论;
【规范解答】(1)解:点的运动速度为,,
点运动到点的时间为4,
点的运动速度为,
点从点出发沿方向顺时针作折线运动到点的时间为,点,相遇时在边上,
,
,
故答案为3.2;
(2)解:如图1,
,
点只能在边上,
四边形是正方形,
,
四边形是平行四边形,
,
,
,
;
(3)解:①当点在边上时,如图2,
,,要使和全等,只能是,
,
,,
,
,
②当点在边时,不能构成,
③当点在边上时,如图3,
同①的方法得,要使和全等,只能是,
,
,
,
④当点在边时,不是直角三角形,而是直角三角形,所以,不能全等;
即:当和全等时,的值为0.8或;
【考察注意点】本题考查四边形综合题、正方形的性质、平行四边形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会分类讨论.
20.(2021春·四川成都·八年级校考期中)已知:在中,,点D为直线上一动点(点D不与B、C重合),以为边作正方形,连接.
(1)如图1,当点D在线段的延长线上时,请你判断线段与的数量关系,并说明理由.
(2)如图1,若,请连接并求出的长.
(3)如图2,当点D在线段的反向延长线上时,且点A、F分别在直线的两侧,其它条件不变;若连接正方形对角线,交点为O,连接,探究的形状,并说明理由.
【答案】(1),理由见解析
(2);
(3)是等腰三角形,理由见解析
【思路引导】(1)设法证明即可求解;
(2)与(1)同理证明,可得,,然后结合图形可得,再根据勾股定理即可得到结论;
(3)根据等腰直角三角形的性质求出,再根据邻补角的定义求出,再根据同角的余角相等求出,然后利用“边角边”证明,再求出,然后根据直角三角形斜边上的中线等于斜边的一半求出,再根据正方形的对角线相等求出,从而得到是等腰三角形.
【规范解答】(1)解:,理由如下,
∵,
∴,
∵四边形是正方形,
∴,
∵,,
∴,
在和中,,
∴,
∴;
(2)解:由(1)得,
∴,,
∴,
∵,则,
∴,
∵,
∴,
∴;
(3)解:是等腰三角形,理由如下,
∵,
∴,
则,
∵四边形是正方形,
∴,,
∵,,
∴,
在和中,,
∴,
∴,
∴,
则为直角三角形,
∵正方形中,O为中点,
∴,
∵在正方形中,,,
∴,
∴是等腰三角形.
【考察注意点】本题考查了四边形的综合题,正方形的性质,全等三角形的判定与性质,等腰直角三角形的性质,等腰三角形的判定,以及同角的余角相等的性质,此类题目通常都是用同一种思路求解,在(1)中找出证明三角形全等的思路是解题的关键.
数学八年级下册19.2.2 一次函数精品达标测试: 这是一份数学八年级下册19.2.2 一次函数精品达标测试,文件包含1922一次函数原卷版docx、1922一次函数解析版docx等2份试卷配套教学资源,其中试卷共87页, 欢迎下载使用。
【重难点讲义】人教版数学八年级下册-19.1 函数 讲义: 这是一份【重难点讲义】人教版数学八年级下册-19.1 函数 讲义,文件包含191函数原卷版docx、191函数解析版docx等2份试卷配套教学资源,其中试卷共89页, 欢迎下载使用。
数学18.2.2 菱形精品练习题: 这是一份数学18.2.2 菱形精品练习题,文件包含1822菱形原卷版docx、1822菱形解析版docx等2份试卷配套教学资源,其中试卷共52页, 欢迎下载使用。













