【重难点讲义】浙教版数学九年级上册-九年级上学期期末测试模拟卷

这是一份【重难点讲义】浙教版数学九年级上册-九年级上学期期末测试模拟卷，文件包含重难点讲义浙教版数学九年级上册-期末测试模拟卷原卷版docx、重难点讲义浙教版数学九年级上册-期末测试模拟卷解析版docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。
九年级上学期期末测试模拟卷
考试范围：初中数学全部；考试时间：120分钟；满分：120分
一、选择题。（共10小题，每小题3分，共30分）
1．（3分）﹣11的相反数是（　　）
A． B．11 C．﹣11 D．﹣
【分析】应用相反数的定义进行求解即可得出答案．
【解答】解：﹣（﹣11）＝11．
故选：B．
2．（3分）“辽宁舰”是中国人民解放军海军第一艘可以搭载固定翼飞机的航空母舰，满载排水量为67500吨，这个数据用科学记数法表示为（　　）
A．0.675×105 B．6.75×104 C．67.5×103 D．675×102
【分析】利用科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解：67500用科学记数法表示为：6.75×104．
故选：B．
3．（3分）已知a≠0，下列运算中正确的是（　　）
A．a+a2＝a3 B．（a3）2÷a2＝a4
C．（a3）2＝a5 D．a2•a3＝a6
【分析】根据同底数幂的乘除运算、积的乘方运算、幂的乘方运算以及合并同类项法则即可求出答案．
【解答】解：A、a与a2不是同类项，故不能合并，故A不符合题意．
B、原式＝a6÷a2＝a4，故B符合题意．
C、原式＝a6，故C不符合题意．
D、原式＝a5，故D不符合题意．
故选：B．
4．（3分）在Rt△ABC中，∠C＝90°，BC＝4，tanB＝2，则AC的长为（　　）
A．2 B．4 C．6 D．8
【分析】利用锐角三角函数求解．
【解答】解：在Rt△ABC中，
∵tanB＝，
∴AC＝tanB•BC＝2×4＝8．
故选：D．
5．（3分）如图，四边形ABCD内接于⊙O，若∠ABC＝129°，则∠AOC的度数为（　　）

A．129° B．120° C．102° D．51°
【分析】由∠D+∠ABC＝180°可求∠D，再由∠AOC＝2∠D即可得到答案．
【解答】解：∵∠D+∠ABC＝180°，
∴∠D＝180°﹣129°＝51°，
∴∠AOC＝2∠D＝102°，
故选：C．
6．（3分）李老师为了了解本班学生每周课外阅读文章的数量，抽取了7名同学进行调查，调查结果如下（单位：篇/周）：4，，2，5，5，4，3，其中有一个数据不小心被墨迹污损．已知这组数据的平均数为4，那么这组数据的众数与中位数分别为（　　）
A．4，5 B．3，5 C．4，4 D．5，4
【分析】设被污损的数据为x，根据这组数据的平均数为4求出x的值，再依据众数和中位数的定义求解可得．
【解答】解：设被污损的数据为x，
则4+x+2+5+5+4+3＝4×7，
解得x＝5，
∴这组数据中出现次数最多的是5，即众数为5篇/周，
将这7个数据从小到大排列为2、3、4、4、5、5、5，
∴这组数据的中位数为4篇/周，
故选：D．
7．（3分）如图，在Rt△AOB中，∠AOB＝90°，OA＝2，OB＝1，将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画和，连接AD，则图中阴影部分的面积是（　　）

A． B． C．π D．5+π
【分析】作DH⊥AE于H，根据勾股定理求出AB，根据阴影部分面积＝△ADE的面积+△EOF的面积+扇形AOF的面积﹣扇形DEF的面积、利用扇形面积公式计算即可．
【解答】解：作DH⊥AE于H，
∵∠AOB＝90°，OA＝2，OB＝1，
∴AB＝＝，
由旋转，得△EOF≌△BOA，
∴∠OAB＝∠EFO，
∵∠FEO+∠EFO＝∠FEO+∠HED＝90°，
∴∠EFO＝∠HED，
∴∠HED＝∠OAB，
∵∠DHE＝∠AOB＝90°，DE＝AB，
∴△DHE≌△BOA（AAS），
∴DH＝OB＝1，
阴影部分面积＝△ADE的面积+△EOF的面积+扇形AOF的面积﹣扇形DEF的面积
＝×3×1+×1×2+﹣
＝﹣π，
故选：B．

8．（3分）已知直线l1：y＝kx+b与直线l2：y＝﹣x+m都经过C（﹣，），直线l1交y轴于点B（0，4），交x轴于点A，直线l2交y轴于点D，P为y轴上任意一点，连接PA、PC，有以下说法：
①方程组的解为；
②△BCD为直角三角形；
③S△ABD＝6；
④当PA+PC的值最小时，点P的坐标为（0，1）．
其中正确的说法是（　　）

A．①②③ B．①②④ C．①③④ D．①②③④
【分析】根据一次函数图象与二元一次方程的关系，利用交点坐标可得方程组的解；根据两直线的系数的积为﹣1，可知两直线互相垂直；求得BD和AO的长，根据三角形面积计算公式，即可得到△ABD的面积；根据轴对称的性质以及两点之间，线段最短，即可得到当PA+PC的值最小时，点P的坐标为（0，1）．
【解答】解：①∵直线l1：y＝kx+b与直线l2：y＝﹣x+m都经过C（﹣，），
∴方程组的解为，
故①正确，符合题意；

②把B（0，4），C（﹣，）代入直线l1：y＝kx+b，可得，解得，
∴直线l1：y＝2x+4，
又∵直线l2：y＝﹣x+m，
∴直线l1与直线l2互相垂直，即∠BCD＝90°，
∴△BCD为直角三角形，
故②正确，符合题意；

③把C（﹣，）代入直线l2：y＝﹣x+m，可得m＝1，
y＝﹣x+1中，令x＝0，则y＝1，
∴D（0，1），
∴BD＝4﹣1＝3，
在直线l1：y＝2x+4中，令y＝0，则x＝﹣2，
∴A（﹣2，0），
∴AO＝2，
∴S△ABD＝×3×2＝3，
故③错误，不符合题意；

④点A关于y轴对称的点为A'（2，0），
由点C、A′的坐标得，直线CA′的表达式为：y＝﹣x+1，
令x＝0，则y＝1，
∴当PA+PC的值最小时，点P的坐标为（0，1），
故④正确，符合题意；
故选：B．
9．（3分）七巧板是我们祖先的一项卓越创造，被西方人誉为“东方魔板”．下面的两幅图正方形（如图1）、“风车型”（如图2）都是由同一副七巧板拼成的，则图中正方形ABCD，EFGH的面积比为（　　）

A． B． C． D．
【分析】设BD＝a+a+a+a＝4a，则CD＝2a，得正方形ABCD的面积，图2中EQ＝3a，FQ＝2a，勾股定理得出EF＝＝，即可得出正方形EFGH的面积，求出面积比值即可．
【解答】解：设BD＝a+a+a+a＝4a，则CD＝BC＝BD•sin45°＝2a，
∴正方形ABCD的面积是（2a）2＝8a2，
图2中，EQ＝3a，FQ＝2a，
由勾股定理得，EF＝＝，
∴正方形EFGH的面积是（a）2＝13a2，
∴图中正方形ABCD，EFGH的面积比为＝，
故选：B．
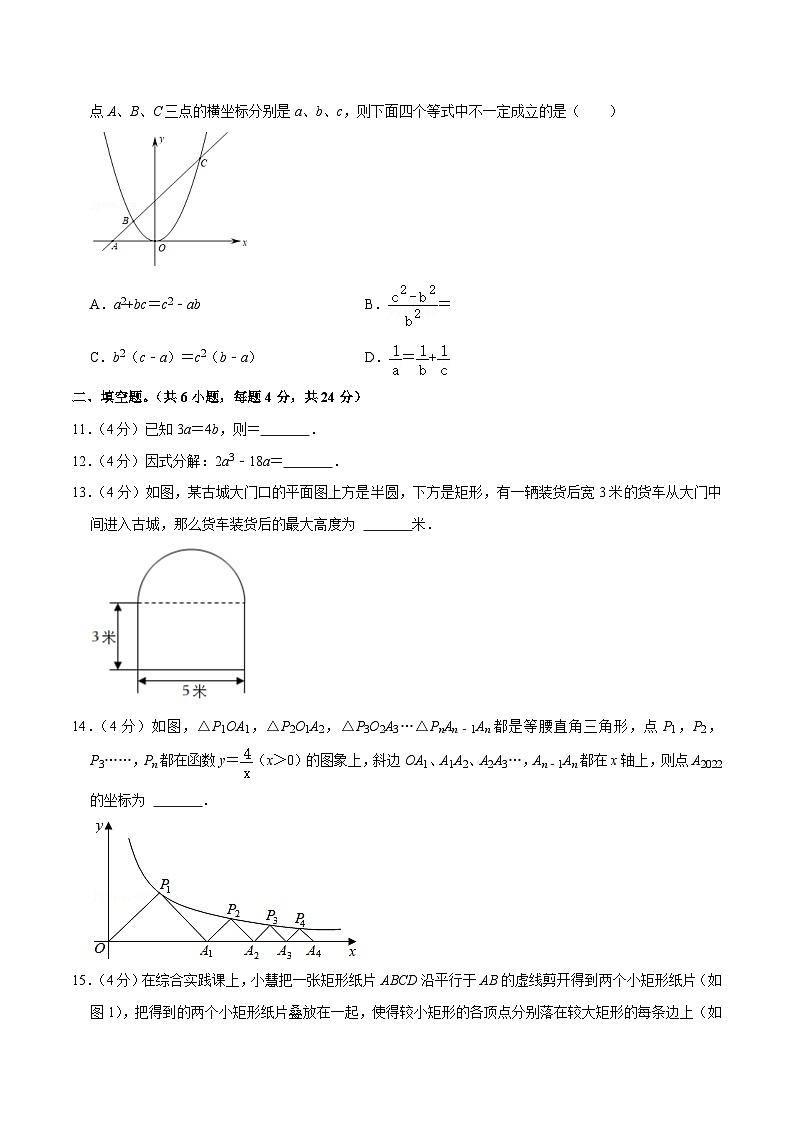
10．（3分）如图在平面直角坐标系中，一次函数y＝mx+n与x轴交于点A，与二次函数交于点B、点C，点A、B、C三点的横坐标分别是a、b、c，则下面四个等式中不一定成立的是（　　）

A．a2+bc＝c2﹣ab B．＝
C．b2（c﹣a）＝c2（b﹣a） D．＝+
【分析】将点A（a，0）坐标代入一次函数表达式，求得一次函数的表达式为y＝mx﹣am，而点B、C在该二次函数上，则，对①②两式进行处理，即可求解．
【解答】解：一次函数y＝mx+n与x轴的轴交于点A，故点（a，0），
将点A（a，0）坐标代入一次函数表达式得：0＝am+n，
解得：n＝﹣am，
故一次函数的表达式为y＝mx﹣am，
∵点B、C在一次函数上，故点B、C的坐标分别为（b，mb﹣ma）、（c，mc﹣ma），
设二次函数的表达式为y＝Ax2，
点B、C在该二次函数上，则，
（1）②﹣①得：A（b2﹣c2）＝m（c﹣b），等式两边同除以Ab2得，，即，故B正确，不符合题意；
（2）①÷②得：③，即C正确，不符合题意；
（3）化简③得：a＝，即＝，故D正确，不符合题意；
（4）化简A得：a2﹣c2＝﹣bc﹣ab，化简得：a+b＝c，而从上述各式看，该式不一定成立，故A符合题意，
故选：A．
二、填空题。（共6小题，每题4分，共24分）
11．（4分）已知3a＝4b，则＝　　．
【分析】通过等式，可以用a表示b，代入分式，约分化简求值．
【解答】解：∵3a＝4b，
∴b＝a，
∴
＝
＝
＝1﹣
＝．
故答案为：．
12．（4分）因式分解：2a3﹣18a＝　2a（a+3）（a﹣3）　．
【分析】先提公因式，然后再利用平方差公式继续分解即可解答．
【解答】解：2a3﹣18a
＝2a（a2﹣9）
＝2a（a+3）（a﹣3），
故答案为：2a（a+3）（a﹣3）．
13．（4分）如图，某古城大门口的平面图上方是半圆，下方是矩形，有一辆装货后宽3米的货车从大门中间进入古城，那么货车装货后的最大高度为 　5　米．

【分析】由已知得OB＝米，OA＝米，在Rt△AOB中，根据勾股定理求出AB，即可求出答案．
【解答】解：如图，O为半圆的圆心，

由已知得OB＝米，OA＝米，
在Rt△AOB中，根据勾股定理，
AB＝＝＝2米，
∴AC＝2+3＝5（米）．
故答案为：5．
14．（4分）如图，△P1OA1，△P2O1A2，△P3O2A3…△PnAn﹣1An都是等腰直角三角形，点P1，P2，P3……，Pn都在函数y＝（x＞0）的图象上，斜边OA1、A1A2、A2A3…，An﹣1An都在x轴上，则点A2022的坐标为 　（4，0）　．

【分析】由于△P1OA1是等腰直角三角形，可知直线OP1的解析式为y＝x，将它与y＝联立，求出方程组的解，得到点P1的坐标，则A1的横坐标是P1的横坐标的两倍，从而确定点A1的坐标；由于△P1OA1，△P2A1A2都是等腰直角三角形，则A1P2∥OP1，直线A1P2可看作是直线OP1向右平移OA1个单位长度得到的，因而得到直线A1P2的解析式，同样，将它与y＝（x＞0）联立，求出方程组的解，得到点P2的坐标，则P2的横坐标是线段A1A2的中点，从而确定点A2的坐标；依此类推，从而确定点A2020的坐标．
【解答】解：过P1作P1B1⊥x轴于B1，
易知B1（2，0）是OA1的中点，
∴A1（4，0）．
可得P1的坐标为（2，2），
∴P1O的解析式为：y＝x，
∵P1O∥A1P2，
∴A1P2的表达式一次项系数相等，
将A1（4，0）代入y＝x+b得4+b＝0，
∴b＝﹣4，
∴A1P2的表达式是y＝x﹣4，
与y＝（x＞0）联立，解得P2（2+2，﹣2+2）．
仿上，A2（4，0）．
P3（2+2，﹣2+2），A3（4，0）．
依此类推，点An的坐标为（4，0），
故点A2022的坐标是（4，0）．
故答案为：（4，0）．

15．（4分）在综合实践课上，小慧把一张矩形纸片ABCD沿平行于AB的虚线剪开得到两个小矩形纸片（如图1），把得到的两个小矩形纸片叠放在一起，使得较小矩形的各顶点分别落在较大矩形的每条边上（如图2）．

（1）若AB＝5，tanα＝，则BC＝　6　．
（2）记＝m，则m的取值范围是 　m＞　．
【分析】（1）依次解直角三角形PCQ和直角三角形FDQ，求得PC，CQ，DQ，FD，进而求得结果；
（2）同（1）方法相同：设PQ＝AB＝a，依次解直角三角形PCQ和直角三角形FDQ，表示出PC，CQ，DQ，FD，进而根据BC＝BT+PT+CP列出关系式，根据三角函数定义求得结果．
【解答】解：（1）如图，

∵tanα＝，
∴sinα＝，cosα＝，
在Rt△PCQ中，PQ＝AB＝5，
∴PC＝PQ•cosα＝5×＝3，CQ＝AB•sinα＝4，
∵四边形ABCD是矩形，
∴CD＝AB＝5，∠C＝∠D＝90°，
∴∠PQC+∠QPC＝90°，
∵∠FQP＝90°，
∴∠FQD+∠PQC＝90°，
∴∠FQC＝∠CPQ＝α，
同理可得：∠TEP＝∠CPQ＝α，
∵∠ETP＝∠D＝90°，FQ＝EP，
∴△FDQ≌△PTE（AAS），
∴PT＝DF，
在Rt△FDQ中，DQ＝CD﹣CQ＝AB﹣CQ＝1，
∴FQ＝，DF＝DQ•tanα＝，
∴PT＝DF＝，BT＝FQ＝，
∴BC＝BT+PT+PC＝＝6，
故答案为：6．
（2）设PQ＝AB＝a，BC＝b，
由（1）可得，
在Rt△PCQ中，
PC＝PQ•cosα＝a•cosα，
CQ＝a•sinα，
DQ＝a﹣a•sinα＝a•（1﹣sinα），
在Rt△FDQ中，
BT＝FQ＝＝，
∴PT＝DF＝FQ•sinα＝，
由BC＝BT+PT+PC得，
b＝++a•cosα
＝2a•cosα，
∴＝，
∵0＜α＜90°，
∴0＜cosα＜1，
∴＞，
即m＞，
故答案为：．
16．（4分）疫情期间在家学习网课时，小李将笔记本电脑水平放置在桌子上，显示屏OB与底板OA所在水平线的夹角为120°，此时感觉最舒适（如图1），侧面示意图为图2．使用时为了散热，他在底板下垫入散热架ACO'后，使电脑变化至AO'B'位置（如图3），侧面示意图为图4．已知OA＝OB＝24cm，O'C⊥OA于点C，O'C＝12cm．

（1）∠CAO′＝　30°　；
（2）显示屏的顶部B′比原来升高了 　15.2　cm．（结果保留到0.1cm，参考数据：≈1.73）
【分析】（1）在Rt△ACO′中，利用∠O′AC的正弦值即可解答；
（2）要求显示屏的顶部B′比原来升高的距离，所以想到过点B作BD⊥AO，交AO的延长线于点D，然后在Rt△BOD中求出BD的长度，最后再证明B′，O′，C三点共线，然后进行计算即可解答．
【解答】解：（1）∵O'C⊥OA，
∴∠ACO′＝90°，
在Rt△ACO′中，O'C＝12cm，O′A＝24cm，
∴sin∠O′AC＝＝＝，
∴∠CAO′＝30°，
故答案为：30°；
（2）过点B作BD⊥AD，交AO的延长线于点D，

∵∠AOB＝120°，
∴∠BOD＝180°﹣∠AOB＝180°﹣120°＝60°，
在Rt△BOD中，BD＝OBsin∠BOD＝24×＝12cm，
∵∠ACO′＝90°，∠CAO′＝30°，
∴∠AO′C＝90°﹣∠CAO′＝60°，
∵∠AO′B＝120°，
∴∠AO′B+∠AO′C＝180°，
∴B′，O′，C在同一条直线上，
∴B′C⊥AC，
∴B′C＝B′O′+O′C＝24+12＝36cm，
∴显示屏的顶部B′比原来升高了：
B′C﹣BD＝36﹣12≈15.2cm，
故答案为：15.2．
三．简答题。（共8小题．17-19每题6分，20、21题8分，22、23每题10分，24题12分）
17．（6分）计算：（﹣2022）0+3+（1﹣3﹣2×18）．
【分析】先计算二次根式、零次幂、负整数指数幂，再计算乘法，最后计算加减．
【解答】解：（﹣2022）0+3+（1﹣3﹣2×18）
＝1+9×+（1﹣×18）
＝1+9+1﹣2
＝9．
18．（6分）如图，在△ABC中，AB＝AC，BE是AC的中线，点D在AC的延长线上，连接BD，BC平分∠EBD．
（1）求证：∠ABE＝∠D；
（2）求证：BD＝2BE．

【分析】（1）根据等边对等角以及角平分线的定义即可推出∠ACB＝∠D+∠DBC＝ABC＝∠ABE+∠CBE＝∠ABE+∠DBC，即可得出结论；
（2）延长BE到点F，使BE＝EF，根据SAS证明△AEB≌△CEF得出∠F＝∠ABE，从而推出∠F＝∠D，再根据AAS证明△BCF≌△DBC即可推出结论．
【解答】证明：（1）∵AC＝AB，
∴∠ACB＝∠ABC，
∵BC平分∠EBD，
∴∠EBC＝∠DBC，
∵∠ACB＝∠D+∠DBC＝ABC＝∠ABE+∠CBE＝∠ABE+∠DBC，
∴∠ABE＝∠D；
（2）如图，延长BE到点F，使BE＝EF，

∵BE是AC的中线，
∴E是AC的中点，
∴AE＝CE，
又∵∠AEB＝∠CEF，BE＝EF，
∴△AEB≌△CEF（SAS），
∴∠F＝∠ABE，
由（1）知，∠ABE＝∠D，
∴∠F＝∠D，
又∵∠DBC＝∠EBC，BC＝BC，
∴△BCF≌△DBC（AAS），
∴BD＝BF，
即BE+EF＝BD，
∵BE＝EF，
∴BD＝2BE．
19．（6分）图①、图②均是3×2的正方形网格，每个小正方形的顶点称为格点，线段AB的端点均在格点上．（只用无刻度的直尺，保留适当的作图痕迹），
（1）在图①中画一个直角△APB，使点P在格点上，且∠ABP的正切值为2．
（2）在图①中画一个锐角△AQC，使点Q在线段AB上，点C在格点上，且∠AQC的正切值为2．

【分析】（1）构造直角△APB，使得AP＝2BP，P在格点上即可；
（2）利用（1）中结论，再根据要求作出满足条件的三角形即可．
【解答】解：（1）如图：

△APB即为所求；
（2）如图：

△AQC即为所求．
20．（8分）2022年4月15日是第七个全民国家安全教育日．为增强师生的国家安全意识，我区某中学组织了“国家安全知识竞赛”，根据学生的成绩划分为A、B、C、D四个等级，并绘制了如下不完整的条形统计图和扇形统计图：

根据图中提供的信息，回答下列问题：
（1）参加知识竞赛的学生共有 　40　人；
（2）扇形统计图中，m＝　10　，C等级对应的圆心角为 　144　度；
（3）小永是四名获A等级的学生中的一位，学校将从获A等级的学生中任选2人，参加区举办的知识竞赛，请用列表法或画树状图，求小永被选中参加区知识竞赛的概率．

【分析】（1）根据D等级的人数和所占的百分比即可得出答案；
（2）用A等级的人数除以总人数，求出m的值，再用360°乘以C等级所占的百分比即可；
（3）根据题意画出树状图得出所有等可能的情况数，找出小永被选中参加区知识竞赛的情况数，然后根据概率公式即可得出答案．
【解答】解：（1）参加知识竞赛的学生共有：12÷30%＝40（人）；
故答案为：40；

（2）m%＝×100%＝10%，即m＝10；
C等级对应的圆心角为：360°×（1﹣20%﹣10%﹣30%）＝144°；
故答案为：10，144；

（3）小永用A表示，其他3名同学分别用B、C、D表示，
根据题意画图如下：

共有12种等可能的情况数，其中小永被选中参加区知识竞赛的有6种，
则小永被选中参加区知识竞赛的概率是＝．
21．（8分）如图，△ABC内接于⊙O，AB是⊙O的直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于点E，交PC于点F，连接AF．
（1）判断直线AF与⊙O的位置关系并说明理由；
（2）若⊙O的半径为6，AF＝2，求AC的长；
（3）在（2）的条件下，求阴影部分的面积．

【分析】（1）连接OC，证明△AOF≌△COF（SAS），由全等三角形的判定与性质得出∠OAF＝∠OCF＝90°，由切线的判定可得出结论；
（2）由直角三角形的性质求出∠AOF＝30°，可得出AE＝OA＝3，则可求出答案；
（3）证明△AOC是等边三角形，求出∠AOC＝60°，OC＝6，由三角形面积公式和扇形的面积公式可得出答案．
【解答】解：（1）直线AF与⊙O相切．
理由如下：连接OC，

∵PC为圆O切线，
∴CP⊥OC，
∴∠OCP＝90°，
∵OF∥BC，
∴∠AOF＝∠B，∠COF＝∠OCB，
∵OC＝OB，
∴∠OCB＝∠B，
∴∠AOF＝∠COF，
∵在△AOF和△COF中，
，
∴△AOF≌△COF（SAS），
∴∠OAF＝∠OCF＝90°，
∴AF⊥OA，
又∵OA为圆O的半径，
∴AF为圆O的切线；
（2）∵∠AOF＝∠COF，OA＝OC，
∴E为AC中点，
即AE＝CE＝AC，OE⊥AC，
∵∠OAF＝90°，OA＝6，AF＝2，
∴tan∠AOF＝，
∴∠AOF＝30°，
∴AE＝OA＝3，
∴AC＝2AE＝6；
（3）∵AC＝OA＝6，OC＝OA，
∴△AOC是等边三角形，
∴∠AOC＝60°，OC＝6，
∵∠OCP＝90°，
∴CP＝OC＝6，
∴S△OCP＝OC•CP＝＝18，S扇形AOC＝＝6π，
∴阴影部分的面积为S△OCP﹣S扇形AOC＝18﹣6π．
22．（10分）某公司以10元/kg的价格收购一批产品进行销售，经过市场调查发现：日销售量y（千克）与销售价格x（元/千克）之间是一次函数关系，当销售价格x是10元/千克时，日销售量y是300千克，当销售价格x是20元/千克时，其销售量y是150千克．
（1）求y与x之间的函数表达式；
（2）该公司应该如何确定这批产品的销售价格，才能使日销售利润W1最大？
（3）若该公司每销售1千克这种产品需支出a元（a＞0）的相关费用，当20≤x≤25时，公司的日获利W2元的最大值为1215，求a的值．
【分析】（1）设y与x之间的函数表达式时y＝kx+b，用待定系数法可得y与x之间的函数表达式；
（2）结合（1）中的结果，列出W1和x的函数关系式，根据二次函数性质可得答案；
（3）根据题意和二次函数的性质，利用分类讨论的方法，可以求得a的值．
【解答】解：（1）设y与x之间的函数表达式时y＝kx+b，
根据题意得：，
解得，
∴y与x之间的函数表达式是y＝﹣15x+450；
（2）由题意可得，
W1＝（x﹣10）（﹣15x+450）＝﹣15（x﹣20）2+1500，
∵﹣15＜0，
∴当x＝20时，W1取最大值，最大值为1500，
∴当售价为20元时，该公司所获最大利润为1500元；
（3）当20≤x≤25时，设获得的利润为w2元，
w2＝（x﹣10﹣a）（﹣15x+450）＝﹣15x2+（600+15a）x﹣450（10+a），
对称轴是直线x＝﹣＝20+a，
当a≥10时，x＝25，w取得最大值，此时w＝1125﹣75a＜1215，不符合题意；
当0＜a＜10时，x＝20+a，w取得最大值，此时w＝﹣15×（20+a）2+（600+15a）（20+a）﹣450（10+a）＝﹣150a+1500，
当w＝1215时，1215＝﹣150a+1500，
解得，a1＝2，a2＝38（舍去），
综上所述，a的值是2．
23．（10分）定义：我们把对角线相等的凸四边形叫做“等角线四边形”．
（1）在已经学过的“①平行四边形；②矩形；③菱形；④正方形”中，一定是“等角线四边形”的是 　②④　（填序号）；
（2）如图1，在正方形ABCD中，点E，F分别在边BC，CD上，且EC＝DF，连接EF，AF，求证：四边形ABEF是等角线四边形；
（3）如图2，已知在△ABC中，∠ABC＝90°，AB＝4，BC＝3，D为线段AB的垂直平分线上一点，若以点A，B，C，D为顶点的四边形是等角线四边形，求这个等角线四边形的面积．

【分析】（1）由矩形和正方形的性质可直接求解；
（2）由“SAS”可证△ABE≌△BCF，可得AE＝BF，可得结论；
（3）分两种情况讨论，由勾股定理求出DE的长，即可求解．
【解答】（1）解：∵矩形、正方形的对角线相等，
∴矩形和正方形是“等角线四边形”，
故答案为②④；
（2）证明：连接AE，BF，

∵四边形ABCD是正方形，
∴AB＝BC＝CD，∠ABC＝∠BCD＝90°，
∵EC＝DF，
∴BE＝CF，
∴△ABE≌△BCF（SAS），
∴AE＝BF，
∴四边形ABEF是等角线四边形；
（3）当点D在AB的上方时，如图，

∵DE是AB的中垂线，
∴AE＝BE＝2，
∵∠ABC＝90°，AB＝4，BC＝3，
∴AC＝5，
∵四边形ABCD为等角线四边形，
∴AC＝BD＝5，
∴DE＝＝＝，
∴S四边形ABCD＝S△ABD+S△BCD＝×AB×DE+×BC×BE＝2+3；
当点D在AB的下方时，如图，过点D作DF⊥BC，交CB的延长线于F，

∵四边形ACBD为等角线四边形，
∴BA＝CD＝4，
∵DE⊥AB，∠ABF＝90°，DF⊥CF，
∴四边形DEBF是矩形，
∴BE＝DF＝2，DE＝BF，
∴CF＝＝＝2，
∴BF＝2﹣3，
∴S四边形ADBC＝S△ABC+S△ABD＝×4×（2﹣3）+×4×3＝4，
综上所述：这个等角线四边形的面积为4或2+3．
24．（12分）如图，矩形ABCD，点P是对角线AC上的动点（不与A、C重合），连接PB，作PE⊥PB交射线DC于点E．已知AD＝6，AB＝8．设AP的长为x．
（1）如图1，PM⊥AB于点M，交CD于点N．求证：△BMP∽△PNE．
（2）试探究：是否是定值？若是，请求出这个值；若不是，请说明理由．
（3）当△PCE是等腰三角形时，请求出所有x的值．


【分析】（1）根据同角的余角相等得到∠PBM＝∠EPN，根据两角相等的两个三角形相似证明结论；
（2）分点E在线段DC上、点E在线段DC的延长线上两种情况，根据相似三角形的性质用x分别表示出BM、PN，计算即可；
（3）分点E在线段DC上、点E在线段DC的延长线上两种情况，根据等腰三角形的性质计算，得到答案．
【解答】（1）证明：∵四边形ABCD为矩形，
∴AB∥CD，
∵PM⊥AB，
∴PM⊥CD，∠PBM+∠BPM＝90°，
∵PE⊥PB，
∴∠EPN+∠BPM＝90°，
∴∠PBM＝∠EPN，
∵∠BMP＝∠PNE＝90°，
∴△BMP∽△PNE；
（2）解：＝，
理由如下：如图1，当点E在线段DC上时，
在Rt△ACD中，AD＝6，DC＝AB＝8，
∴AC＝＝10，
∵PM⊥AB，∠ABC＝90°，
∴PM∥BC，
∴＝，即＝，
解得：BM＝8﹣x，
同理：△CPN∽△CAD，
∴＝，即＝，
解得：PN＝6﹣x，
∵△BMP∽△PNE，
∴＝＝＝，
如图2，当点E在线段DC的延长线上时，
同上方法可以证明＝，
综上所述，为定值；
（3）如图3，当点E在线段DC上时，△PCE是等腰三角形时，只能是EP＝EC，
连接BE交PC于F，
∵EP＝EC，
∴∠EPC＝∠ECP，
∵∠BPE＝∠BCE＝90°，
∴∠BPC＝∠BCP，
∴BP＝BC，
∴BE垂直平分CP，
∵∠ABC＝90°，BF⊥AC，
∴BC2＝CF•AC，
∴CF＝＝＝，
∴CP＝2CF＝，
∴AP＝AC﹣CP＝，
如图2，当点E在线段DC的延长线上时，△PCE是等腰三角形时，只能是CP＝EC，
∴∠CPE＝∠CEP，
∵∠PFB＝∠CFE，
∴∠PBF＝∠CEP，
∴∠ABP＝∠APB，
∴AP＝AB＝8，
综上所述，当△PCE是等腰三角形时，x的值为或8．