【重难点讲义】浙教版数学八年级下册-八年级数学下学期期末测试模拟卷02

这是一份【重难点讲义】浙教版数学八年级下册-八年级数学下学期期末测试模拟卷02，文件包含重难点讲义浙教版数学八年级下册-八年级数学下学期期末测试模拟卷02原卷版docx、重难点讲义浙教版数学八年级下册-八年级数学下学期期末测试模拟卷02解析版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。

浙教版八年级下学期期末考试模拟卷
（考试范围：八下第1-6单元 考试试卷：120分钟 试卷满分：120分）
一、选择题（本题有10小题，每小题3分，共30分）
1．下列二次根式中，是最简二次根式的是（　　）
A． B． C． D．
【分析】最简二次根式的概念：（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式．根据最简二次根式的概念解答即可．
【解答】解：A选项被开方数是小数，可以化成分数，有分母，不符合题意；
B选项的被开方数含分母，不符合题意；
C选项是最简二次根式，符合题意；
D选项的被开方数中有能开的尽方的因数4，不符合题意；
故选：C．
2．在某校冬季运动会上，有15名选手参加了200米预赛，取前八名进入决赛．已知参赛选手成绩各不相同，某选手要想知道自己是否进入决赛，除了知道自己的成绩外，还需要了解全部成绩的（　　）
A．平均数 B．中位数 C．众数 D．方差
【分析】中位数是一组数据最中间一个数或两个数据的平均数；15人成绩的中位数是第8名的成绩．参赛选手要想知道自己是否能进入前8名，只需要了解自己的成绩以及全部成绩的中位数，比较即可．
【解答】解：由于总共有15个人，且他们的分数互不相同，第8的成绩是中位数，所以要判断是否进入前8名，只需要了解自己的成绩以及全部成绩的中位数．
故选：B．
3．用配方法解方程3x2﹣6x+2＝0，将方程变为（x﹣m）2＝的形式，则m的值为（　　）
A．9 B．﹣9 C．1 D．﹣1
【分析】方程整理后，利用完全平方公式配方得到结果，即可求出m的值．
【解答】解：方程3x2﹣6x+2＝0，
变形得：x2﹣2x＝﹣，
配方得：x2﹣2x+1＝，即（x﹣1）2＝，
则m＝1．
故选：C．
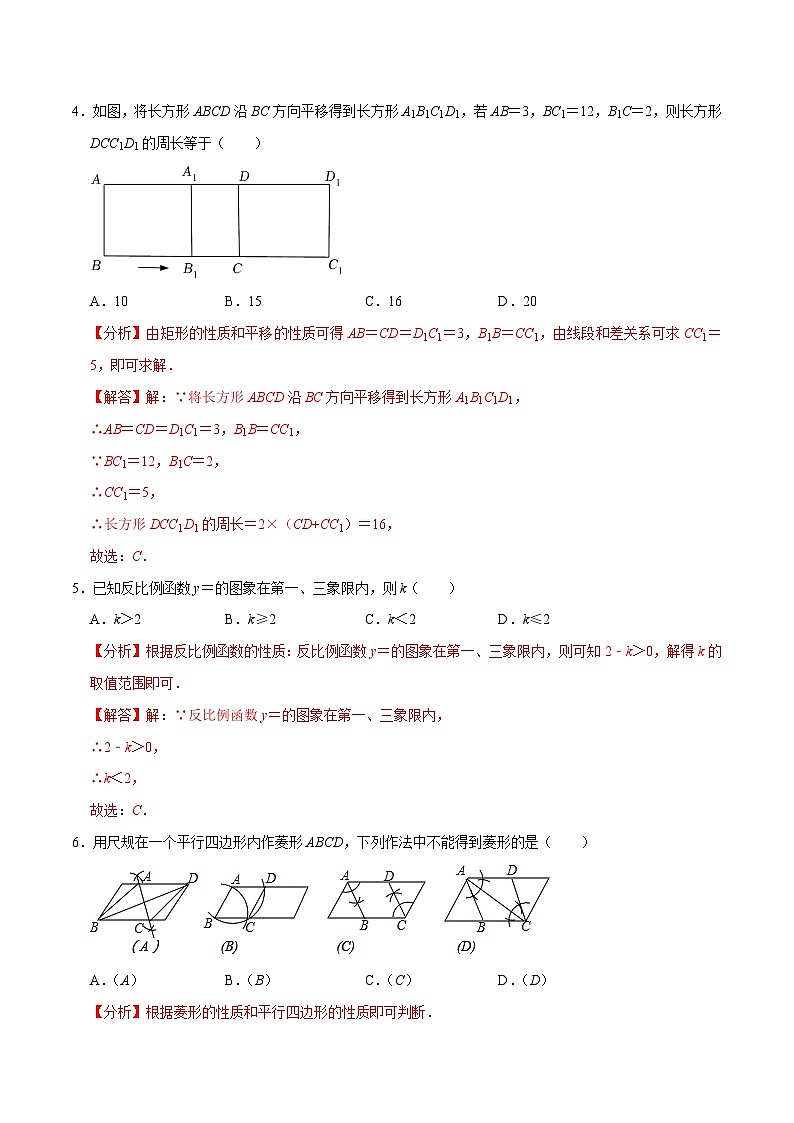
4．如图，将长方形ABCD沿BC方向平移得到长方形A1B1C1D1，若AB＝3，BC1＝12，B1C＝2，则长方形DCC1D1的周长等于（　　）

A．10 B．15 C．16 D．20
【分析】由矩形的性质和平移的性质可得AB＝CD＝D1C1＝3，B1B＝CC1，由线段和差关系可求CC1＝5，即可求解．
【解答】解：∵将长方形ABCD沿BC方向平移得到长方形A1B1C1D1，
∴AB＝CD＝D1C1＝3，B1B＝CC1，
∵BC1＝12，B1C＝2，
∴CC1＝5，
∴长方形DCC1D1的周长＝2×（CD+CC1）＝16，
故选：C．
5．已知反比例函数y＝的图象在第一、三象限内，则k（　　）
A．k＞2 B．k≥2 C．k＜2 D．k≤2
【分析】根据反比例函数的性质：反比例函数y＝的图象在第一、三象限内，则可知2﹣k＞0，解得k的取值范围即可．
【解答】解：∵反比例函数y＝的图象在第一、三象限内，
∴2﹣k＞0，
∴k＜2，
故选：C．
6．用尺规在一个平行四边形内作菱形ABCD，下列作法中不能得到菱形的是（　　）

A．（A） B．（B） C．（C） D．（D）
【分析】根据菱形的性质和平行四边形的性质即可判断．
【解答】解：（A）如图，由作图过程可知：OB＝OD，

∵AD∥BC，
∴∠ADO＝∠CBO，∠DAO＝∠BCO，
∴△ADO≌△CBO（AAS），
∴AD＝BC，AD∥BC，
∴四边形ABCD是平行四边形，
根据线段的垂直平分线的性质可知AB＝AD，
所以一组邻边相等的平行四边形是菱形；符合题意；
（B）∵AD∥BC且AD＝BC，
∴四边形ABCD是平行四边形，
∴AB＝CD，
∴AB＝BC＝CD＝DA，
根据四条边相等的四边形是菱形，符合题意；
（C）如图，由作图过程可知：∠EAB＝∠FAB，∠ECD＝∠FCD，

∵四边形AECF是平行四边形，
∴∠EAF＝∠FCE，AE＝CF，∠E＝∠F，
∴∠EAB＝∠FCD，
∴△AEB≌△CFD（ASA），
∴BE＝DF，AB＝DC，
∵AF＝EC，
∴AD＝BC，
∴四边形ABCD是平行四边形，
根据两组对边分别相等的四边形是平行四边形，不是菱形，不符合题意；
（D）如图，根据作图过程可知：
∠DAC＝∠BAC，∠DCA＝∠BCA，
∵AC＝AC，
∴△ADC≌△ABC（ASA），
∴∠ABC＝∠ADC，AD＝AB，
∴∠ABE＝∠CDF，

∵四边形AECF是平行四边形，
∴AE＝CF，∠E＝∠F，
∴△ABE≌△CDF（AAS），
∴BE＝DF，
∴BC＝AD，
∵BC∥AD，
∴四边形ABCD是平行四边形，
∵AB＝AD，
∴根据一组邻边相等的平行四边形是菱形，符合题意．
故选：C．
7．关于x的一元二次方程kx2﹣2x﹣1＝0有两个不相等实数根，则k的取值范围是（　　）
A．k＞﹣1 B．k＜﹣1 C．k＞1 D．k＞﹣1且k≠0
【分析】方程有两个不相等的实数根，则Δ＞0，由此建立关于k的不等式，然后可以求出k的取值范围．
【解答】解：由题意知k≠0，Δ＝4+4k＞0，
解得k＞﹣1且k≠0．
故选：D．
8．用反证法证明“若实数a，b满足ab＝0，则a，b中至少有一个是0”时，应先假设（　　）
A．a，b中至多有一个是0 B．a，b中至少有两个是0
C．a，b中没有一个是0 D．a，b都等于0
【分析】反证法的步骤中，第一步是假设结论不成立，反面成立，可据此进行解答．
【解答】解：“若实数a、b满足ab＝0，则a、b中至少有一个是0．”第一步应假设：a、b都不等于0．
故选：C．
9．如图是同一直角坐标系中函数y1＝2x和y2＝的图象．观察图象可得不等式2x＞的解集为（　　）

A．﹣1＜x＜1 B．x＜﹣1或x＞1
C．x＜﹣1或0＜x＜1 D．﹣1＜x＜0或x＞1
【分析】结合图象，数形结合分析判断．
【解答】解：由图象，函数y1＝2x和y2＝的交点横坐标为﹣1，1，
∴当﹣1＜x＜0或x＞1时，y1＞y2，即2x＞，
故选：D．
10．如图所示，正方形BCGF，HGDE，FHMN内接于五边形ABCDE，该五边形是轴对称图形，AB与AE为对称边，∠A＝90°，AN＝AM，则的值是（　　）

A． B． C． D．
【分析】连结并延长AG分别交MN、FH、CD于点K、L、P，先证明直线AG是五边形ABCDE的对称轴，则AK⊥MN，FL⊥AG，GP⊥CD；再证明△PCG≌△LGF，得CP＝GL，则CD＝2CP＝2GL；连结AF，作BR⊥AG于点R，延长NF交BR于点Q，连结FR，证明△BQF≌△GLF，得QF＝LF，即可证明四边形QRLF是正方形，则∠BRF＝∠ARF，再证明△BRF≌△ARF，得BF＝AF＝GF，所以AL＝GL，则CD＝2AL；设正方形FHMN的边长为2m，推导出AN＝m，CD＝6m，即可求出的值．
【解答】解：如图，连结并延长AG分别交MN、FH、CD于点K、L、P，
∵∠A＝90°，AN＝AM，
∴∠ANM＝∠AMN＝45°，
∵AB与AE为对称边，
∴AB＝AE，
∴NB＝ME，
∵四边形FHMN、四边形BCGF、四边形HGDE都是正方形，
∴NF＝MH，∠FNM＝∠HMN＝90°，∠CGF＝∠BFG＝90°，
∴∠BNF＝∠EMH＝45°，
∴△BNF≌△EMH（SAS），
∴BF＝EH，
∴GF＝GH＝CG＝DG，
∴直线AG是五边形ABCDE的对称轴，
∴AK⊥MN，FL⊥AG，GP⊥CD，
∴∠CPG＝∠GLF＝90°，
∴∠PCG＝∠LGF＝90°﹣∠PGC，
∵CG＝GF，
∴△PCG≌△LGF（AAS），
∴CP＝GL，
∴CD＝2CP＝2GL；
连结AF，作BR⊥AG于点R，延长NF交BR于点Q，连结FR，
∵BR∥FH∥MN，
∴∠BQF＝∠QFL＝∠FNM＝90°，
∴∠BQF＝∠GLF，∠BFQ＝∠GFL＝90°﹣∠GFQ，
∵BF＝GF，
∴△BQF≌△GLF（AAS），
∴QF＝LF，
∵∠QRL＝∠RLF＝∠QFL＝90°，
∴四边形QRLF是正方形，
∴QF＝LF，QR＝LR，
∵FR＝RF，
∴△QFR≌△LFR（SSS），
∴∠BRF＝∠ARF，
∵∠RBA＝∠ANM＝45°，
∴∠RAB＝∠RBA＝45°，
∴BR＝AR，
∵FR＝FR，
∴△BRF≌△ARF（SAS），
∴BF＝AF＝GF，
∴AL＝GL，
∴CD＝2AL；
设正方形FHMN的边长为2m，则MN＝FN＝2m，AK＝NK＝MN＝m，
∵∠AKN＝90°，
∴AN＝＝＝m，
∵∠LKN＝∠KNF＝∠NFL＝90°，
∴四边形KNFL是矩形，
∴KL＝FN＝2m，
∴CD＝2AL＝2（AK+KL）＝2（m+2m）＝6m，
∴＝＝3，
∴的值是3，
故选：A．
二、填空题（本题共有6个小题，每小题4分，共24分）
11．二次根式中字母x的取值范围是 　x≥1　．
【分析】二次根式有意义的条件就是被开方数是非负数，即可求解．
【解答】解：根据题意得：x﹣1≥0，
解得x≥1．
故答案为：x≥1．
12．一个多边形的内角和是720°，这个多边形的边数是 　6　．
【分析】根据内角和定理180°•（n﹣2）即可求得．
【解答】解：∵多边形的内角和公式为（n﹣2）•180°，
∴（n﹣2）×180°＝720°，
解得n＝6，
∴这个多边形的边数是6．
故答案为：6．
13．数据1，2，2，2，3的方差是 　　．
【分析】先计算出这组数据的平均数，再根据方差的计算公式列式计算即可．
【解答】解：∵这组数据的平均数为＝2，
∴这组数据的方差为×[（2﹣1）2+3×（2﹣2）2+（2﹣3）2]＝．
故答案为：．
14．为增强学生身体素质，某校开展篮球比赛，赛制为单循环形式（每两队之间赛一场）．现计划安排36场比赛，应安排多少个球队参赛？设安排x个球队参赛，根据题意，可列方程为 　x（x﹣1）＝36　．
【分析】利用比赛的总场次数＝参赛队伍数×（参赛队伍数﹣1）÷2，即可得出关于x的一元二次方程，此题得解．
【解答】解：依题意得：x（x﹣1）＝36．
故答案为：x（x﹣1）＝36．
15．如图，等腰△ABC中，AB＝AC＝5，BC＝8，点B在y轴上，BC∥x轴，反比例函数y＝（k＞0，x＞0）的图象经过点A，交BC于点D．若AB＝BD，则四边形ABOC的周长为 　22+4　．

【分析】作AE⊥BC于E，根据等腰三角形的性质得出BE＝CE＝4，利用勾股定理求得AE＝3，从而得出A（4，3+a），D（5，a），由图象上点的坐标特征得出4（3+a）＝5a，解得：a＝12，进而即可求得结论．
【解答】解：作AE⊥BC于E，
∵AB＝AC＝5，BC＝8，
∴BE＝CE＝4，
∴AE＝＝3，
设OB＝a，
∵BD＝AB＝5，
∴A（4，3+a），D（5，a），
∵反比例函数y＝（k＞0，x＞0）的图象经过点A，交BC于点，
∴4（3+a）＝5a，
解得：a＝12，
∴OB＝12，
∴OC＝＝＝4，
∴四边形ABOC的周长＝AB+OB+OC+AC＝5+12+4+5＝22+4．
故答案为：22+4．

16．如图，矩形ABCD中，点E，F，G分别在CD，AD，BC边上，CE＝2，DE＝1，BE平分∠FBC，∠BEF＝∠BEG＝45°，则线段DF的长为 　2　，线段BC的长为 　6　．

【分析】根据∠BE平分∠FBC可得∠FBE＝∠GBE，由于∠BEF＝∠BEG＝45°，则可判定△BEF≌△BEG，根据全等三角形的性质可得EF＝GE，进一步可判定△DEF≌△CGE，则DF＝CE＝2，CG＝1，然后利用勾股定理求出BC即可．
【解答】解：∵∠BE平分∠FBC，
∴∠FBE＝∠GBE，
∵∠BEF＝∠BEG＝45°，BE＝BE，
∴△BEF≌△BEG（ASA），
∴EF＝GE，BF＝BG，
∵四边形ABCD是矩形，
∴∠C＝∠D，AD＝BC，
∵∠BEF＝∠BEG＝45°，
∴∠FEG＝90°，
∴∠GEC+∠DEF＝90°，
∵∠DFE+∠DEF＝90°，
∴∠GEC＝∠DFE，
∴△DEF≌△CGE（AAS），
∴DF＝CE＝2，CG＝DE＝1，
设AD＝BC＝x，则AF＝x﹣2，BG＝x﹣1，
∵BF＝BG，
∴AB2+AF2＝BG2，
即32+（x﹣2）2＝（x﹣1）2，
解得x＝6，
∴BC＝6．
故答案为：2；6．

三、解答题（本大题共8小题，第17、18、19题各6分，第20、21题各8分，第22、23题各10分，第24题12分，共66分）
17．计算：
（1）．
（2）．
【分析】（1）先把二次根式化为最简二次根式，然后合并即可；
（2）先利用多项式乘多项式展开，然后合并即可．
【解答】解：（1）原式＝3﹣5+
＝﹣；
（2）原式＝3﹣5+3﹣﹣2
＝﹣2．
18．解下列方程：
（1）x2+4x﹣1＝0；
（2）（x﹣1）（x+3）＝5（x﹣1）．
【分析】（1）利用公式法求解即可；
（2）利用因式分解法求解即可．
【解答】解：（1）∵a＝1，b＝4，c＝﹣1，
∴△＝42﹣4×1×（﹣1）＝20＞0，
则x＝＝＝﹣2，
即x1＝﹣2+，x2＝﹣2﹣；

（2）∵（x﹣1）（x+3）﹣5（x﹣1）＝0，
∴（x﹣1）（x﹣2）＝0，
则x﹣1＝0或x﹣2＝0，
解得x1＝1，x2＝2．
19．如图，一次函数y＝kx+b的图象交反比例函数y＝图象于A（，4），B（3，m）两点．
（1）求m，n的值；
（2）点E是y轴上一点，且S△AOB＝S△EOB，求E点的坐标；
（3）请你根据图象直接写出不等式kx+b＞的解集．

【分析】（1）把点A（，4）代入y＝中，利用待定系数法求得n的值，即可求得反比例函数的解析式，进而把B（3，m）代入求得的解析式，即可求得m的值；根据待定系数法即可求得直线CD的表达式；
（2）根据待定系数法即可求得直线AB的表达式，即可求得直线与y轴的交点，根据S△AOB＝S△BOD﹣S△AOD求得△AOB的面积，设E点的坐标为（0，a），根据S△AOB＝S△EOB得到关于a的方程，解方程求得a，从而求得E点的坐标；
（3）根据图象即可求得．
【解答】（1）把点A（，4）代入y＝中，得：n＝×4＝6，
∴反比例函数的解析式为y＝，
将点B（3，m）代入y＝得m＝＝2；
（2）设直线AB的表达式为y＝kx+b，
把A（，4），B（3，2）代入得，
解得
∴直线AB的表达式为y＝﹣x+6，
∴D点的坐标为（0，6），
∴S△AOB＝S△BOD﹣S△AOD＝6×3﹣6×＝，
设E点的坐标为（0，a），
∵S△AOB＝S△EOB，
∴|a|×3＝，
解得：|a|＝3，
∴E点的坐标为（0，3）或（0，﹣3）；
（3）不等式kx+b＞的解集是x＜0或＜x＜3．

20．某学校组织七、八年级全体学生举行了安全知识竞赛活动，为了解竞赛成绩情况，为两个年级各随机抽取10名学生的成绩（满分为100分）进行了分析，并依据分析结果绘制了如下表所示的不完整统计表：
七年级：90，95，95，80，85，90，80，90，85，100；
八年级：85，85，95，80，95，90，90，90，100，90．
年级
平均数
中位数
众数
方差
七年级
89
m
90
39
八年级
n
90
p
q
根据以上信息解答下面问题：
（1）填空：m＝　90　，p＝　90　；
（2）求q的值；
（3）通过数据分析，你认为哪个年级的成绩比较好？说明理由．
【分析】（1）利用中位数和众数的方法求解；
（2）先计算平均数，再利用方差公式计算；
（3）对比各个统计量的大小，结合各个统计量所反映数据的变化特点，做出判断即可．
【解答】解：（1）把七年级的成绩从小到大排列为80，80，85，85，90，90，90，95，95，100，
∴中位数m＝＝90；
八年级成绩中90最多有4个，所以众数p＝90．
故答案为：90，90．
（2）八年级的平均数n＝×（85×2+95×2+90×4+80+100）＝90，
方差为q＝×[2×（85﹣90）2+2×（95﹣90）2+4×（90﹣90）2+（80﹣90）2+（100﹣90）2]＝30．
（3）从平均分来看八年级高；通过方差来看，八年级的方差小，说明八年级的成绩稳定，所以八年级比较好．
21．如图，在▱ABCD中，点G，H分别是AB，CD的中点，点E，F在对角线AC上，且AE＝CF．
（1）求证：四边形EGFH是平行四边形；
（2）连接BD交AC于点O，若BD＝10，AE+CF＝EF，求EG的长．

【分析】（1）先由平行四边形的性质及点G，H分别是AB，CD的中点，得出△AGE和△CHF全等的条件，从而判定△AGE≌△CHF（SAS），然后由全等三角形的性质和角的互补关系得出GE＝HF，GE∥HF，则可得出结论．
（2）先由平行四边形的性质及BD＝10，得出OB＝OD＝5，再根据AE＝CF、AE+CF＝EF及OA＝OC得出AE＝OE，从而可得EG是△ABO的中位线，利用中位线定理可得EG的长度．
【解答】解：（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠GAE＝∠HCF，
∵点G，H分别是AB，CD的中点，
∴AG＝CH，
∵AE＝CF，
∴△AGE≌△CHF（SAS），
∴GE＝HF，∠AEG＝∠CFH，
∴∠GEF＝∠HFE，
∴GE∥HF，
又∵GE＝HF，
∴四边形EGFH是平行四边形；
（2）连接BD交AC于点O，如图：

∵四边形ABCD是平行四边形，
∴OA＝OC，OB＝OD，
∵BD＝10，
∴OB＝OD＝5，
∵AE＝CF，OA＝OC，
∴OE＝OF，
∵AE+CF＝EF，
∴2AE＝EF＝2OE，
∴AE＝OE，
又∵点G是AB的中点，
∴EG是△ABO的中位线，
∴EG＝OB＝2.5．
∴EG的长为2.5．
22．某超市销售一种商品，每件成本为50元，销售人员经调查发现，销售单价为100元时，每月的销售量为50件，而销售单价每降低2元，则每月可多售出10件，且要求销售单价不得低于成本．
（1）当销售单价为90元时，每月的销售量为 　100　件．
（2）求该商品每月的销售量y（件）与销售单价x（元）之间的函数关系式；（不需要求自变量取值范围）
（3）若使该商品每月的销售利润为4000元，并使顾客获得更多的实惠，销售单价应定为多少元？
【分析】（1）根据实际销量＝原销售量+10×列式计算即可；
（2）根据以上等量关系求解即可；
（3）根据“每月销售利润＝实际销售量×（实际售价﹣每件成本）”列出方程，再进一步求解即可．
【解答】解：（1）当销售单价为90元时，每月的销售量为50+10×＝100（件），
故答案为：100；

，
∴y与x的函数关系式为y＝﹣5x+550；

（3）依题意得：y（x﹣50）＝4000，
即（﹣5x+550）（x﹣50）＝4000，
解得：x1＝70，x2＝90，
∵70＜90，
∴当该商品每月销售利润为4000，为使顾客获得更多实惠，销售单价应定为70元．
23．如图，在正方形ABCD中，F为BC为边上的定点，E、G分别是AB、CD边上的动点，AF和EG交于点H．有2个选项：①AF⊥EG②AF＝EG．
（1）请从2个选项中选择一个作为条件，余下一个作为结论，得到一个真命题，并证明．你选择的条件是 　①　，结论是 　②　（只要填写序号）；
（2）若AB＝6，BF＝2．
①若BE＝3，求AG的长；
②连结AG、EF，直接写出AG+EF的最小值．

【分析】（1）条件是①，结论是②．过点G作GP⊥AB交于P，证明△ABF≌△GPE（ASA）即可；
（2）①在Rt△APG中，求出AP＝1，PG＝6，利用勾股定理得出AG＝；
②过点F作FQ∥EG，过点G作GQ∥EF，当A、G、Q三点共线时，AG+EF的值最小，证明△AFQ是等腰直角三角形，由勾股定理即可求AQ的值即为所求．
【解答】解：（1）（答案不唯一）选择的条件是①，结论是②．理由如下：
如图1，过点G作GP⊥AB交于P，
∵AH⊥EG，
∴∠AEH+∠DAH＝90°，
∵∠PEG+∠PGC＝90°，
∴∠EAH＝∠PGE．
在△ABF与△GPE中，
，
∴△ABF≌△GPE（ASA），
∴AF＝EG．
故答案为：①，②（答案不唯一）；
（2）①∵BF＝2，
∴PE＝2，
∵AB＝6，BE＝3，
∴AE＝3，
∴AP＝1，
在Rt△APG中，AP＝1，PG＝6，
∴AG＝＝；
②过点F作FQ∥EG，过点G作GQ∥EF，
∴四边形EFQG为平行四边形，
∴GQ＝EF，
∴AG+EF＝AG+GQ≥AQ，
∴当A、G、Q三点共线时，AG+EF的值最小，
∵EG＝AF，EG＝FQ，
∴AF＝FQ，
∵AF⊥EG，
∴AF⊥FQ，
∴△AFQ是等腰直角三角形，
∵AF＝＝2，
∴AQ＝4，
∴AG+EF的最小值为4．


24．如图，在平面直角坐标系xOy中，一次函数y＝x+3的图象与x轴、y轴分别交于点A、B，M是一次函数y＝x图象上一个动点，将△ABO绕点M顺时针方向旋转90°得到△CDE（点C、D、E分别与点A、B、O对应），CE边恰好落在y轴上．
（1）若点M（0，0），直接写出点C的坐标是 　（0，4）　；
（2）①如图1，若点C（0，6），求点M的坐标；
②若点C（0，c），点M（m，m），直接写出c与m的函数表达式是 　c＝4+2m　．
（3）若在平面内存在一点F，使得以A、B、C、F为顶点的四边形是菱形，直接写出点M的坐标．

【分析】（1）利用旋转的性质求得线段OC即可；
（2）①连接AM，CM，过点M作MG⊥x轴于点G，MF⊥y轴于点F，通过证明Rt△AMG≌Rt△CMF，得到AG＝CF，设M（m，m），此时m＞0，OG＝OF＝m，利用OC＝6，列出关于m的方程即可求解；
②分点M在第一象限和点M在第三象限两种情况讨论解答，利用（2）①中的方法解答即可；
（3）分四种情形讨论解答，画出符合题意的图形，通过计算OC的长度得到点C的坐标，利用c＝4+2m的关系式求得m值，即可得到点M坐标．
【解答】解：（1）对于一次函数y＝x+3，
令x＝0，则y＝3，
∴B（0，3）．
令y＝0，则x+3＝0，
∴x＝﹣4，
∴A（﹣4，0），
∴OA＝4，
若点M（0，0），由题意：点M与点O重合，
∴OC＝OA＝4，
∴C（0，4）．
故答案为：（0，4）；
（2）①连接AM，CM，过点M作MG⊥x轴于点G，MF⊥y轴于点F，如图，

由题意得：MC＝MA，∠AMC＝90°．
∵点M是一次函数y＝x图象上一个动点，
∴设M（m，m），此时m＞0，
∴OG＝OF＝m，
∵MG⊥x轴，MF⊥y轴，∠COG＝90°，
∴四边形FOGM为正方形，
∴MG＝MF＝m．
在Rt△AMG和Rt△CMF中，
，
∴Rt△AMG≌Rt△CMF（HL）．
∴AG＝CF，
∵点C（0，6），
∴OC＝6．
∵AG＝OA+OG＝4+m，
∴CF＝4+m，
∵OC＝CF+OF，
∴4+m+m＝6．
解得：m＝1，
∴M（1，1）；
②当点M在第一象限时，
由①知：AG＝CF，如图，

∵点C（0，c），点M（m，m），
∴OC＝c，OF＝OG＝m，
∴OC＝CF+OF＝AG+OF＝OA+2OF，
∴c＝4+2m；
当点M在第一象限时，
连接AM，CM，过点M作MG⊥x轴于点G，MF⊥y轴于点F，如图，

同（2）的方法可得：Rt△AMG≌Rt△CMF，
∴AG＝CF，
∵点C（0，c），点M（m，m），
∴OC＝﹣c，OF＝OG＝﹣m，
∴AG＝OA﹣OG＝4+m，
∴OC＝OF﹣CF＝OF﹣AG＝﹣m﹣（4+m），
∴﹣c＝﹣4﹣2m，
∴c＝4+2m．
综上，c与m的函数表达式是c＝4+2m．
故答案为：c＝4+2m；
（3）当四边形ABCF为菱形时，如图，

∵OA＝4，OB＝3，
∴AB＝＝5，
∴BC＝AB＝5，
∴OC＝BC﹣OB＝2，
∴C（0，﹣2）．
由（2）②的结论可得：
﹣2＝4+2m，
∴m＝﹣3．
∴M（﹣3，﹣3）；
当四边形ABCF为菱形时，如图，

则BC＝AB＝5，
∴OC＝OB+BC＝8，
∴C（0，8）．
由（2）②的结论可得：
8＝4+2m，
∴m＝2．
∴M（2，2）；
当四边形ABFC为菱形时，如图，

则OB＝OC＝3，
∴C（0，﹣3），
由（2）②的结论可得：
﹣3＝4+2m，
∴m＝﹣．
∴M（﹣，﹣）；
当四边形AFBC为菱形时，如图，

连接FC，则CH⊥AB，AH＝BH＝，
∵∠BHC＝∠BOA＝90°，∠HBO＝∠OBA，
∴△BHC∽△BOA，
∴，
∴BC＝．
∴OC＝BC﹣OB＝．
∴C（0，﹣）．由（2）②的结论可得：
﹣＝4+2m，
∴m＝﹣．
∴M（﹣，﹣）．
解法二：连接FC，则CH⊥AB，AH＝BH，
∴AC＝BC．
设OC＝a，则BC＝OC+OB＝a+3，
∴AC＝BC＝a+3．
∵OA2+OC2＝AC2，
∴42+a2＝（a+3）2，
解得：a＝．
∴C（0，﹣）．
由（2）②的结论可得：
﹣＝4+2m，
∴m＝﹣．
∴M（﹣，﹣）．
综上，使得以A、B、C、F为顶点的四边形是菱形，则点M的坐标为（2，2）或（﹣3，﹣3）或（﹣，﹣）或（﹣，﹣）．