【重难点讲义】浙教版数学八年级下册-第07讲 三角形的中位线专题复习

这是一份【重难点讲义】浙教版数学八年级下册-第07讲 三角形的中位线专题复习，文件包含重难点讲义浙教版数学八年级下册-第07讲三角形的中位线专题复习原卷版docx、重难点讲义浙教版数学八年级下册-第07讲三角形的中位线专题复习解析版docx等2份试卷配套教学资源，其中试卷共36页， 欢迎下载使用。

第7讲 三角形的中位线专题探究
类型一 三角形中位线定理
【知识点睛】
三角形中位线定理的应用
（1）证明平行问题;
（2）证明一边是另一边的2倍或
（3）解决"中点问题".
注意∶在处理这些问题时，要求出现三角形及其中位线：
①有中点连线而无三角形，要作辅助线产生三角形;
②有三角形而无中位线，要作中点的连线或过中点作平行线.
【类题训练】
1．如图，四边形ABCD中，AB∥CD，AB＝5，DC＝11，AD与BC的和是12，点E、F、G分别是BD、AC、DC的中点，则△EFG的周长是（　　）

A．8 B．9 C．10 D．12
【分析】连接AE，并延长交CD于K，根据平行线的性质得到∠BAE＝∠DKE，∠ABD＝∠EDK，根据三角形中位线的性质得到BE＝DE，根据全等三角形的性质得到DK＝AB，AE＝EK，EF为△ACK的中位线，求得EF＝CK＝（DC﹣DK）＝（DC﹣AB），根据三角形的中位线得到EG＝BC，FG＝AD，根据三角形的周长得到即可得到结论．
【解答】解：连接AE，并延长交CD于K，
∵AB∥CD，
∴∠BAE＝∠DKE，∠ABD＝∠EDK，
∵点E、F、G分别是BD、AC、DC的中点．
∴BE＝DE，
在△AEB和△KED中，，
∴△AEB≌△KED（AAS），
∴DK＝AB，AE＝EK，EF为△ACK的中位线，
∴EF＝CK＝（DC﹣DK）＝（DC﹣AB），
∵EG为△BCD的中位线，
∴EG＝BC，
又FG为△ACD的中位线，
∴FG＝AD，
∴EG+GF＝（AD+BC），
∵AD+BC＝12，AB＝5，DC＝11，即DC﹣AB＝6，
∴EG+GF＝6，FE＝3，
∴△EFG的周长是6+3＝9．
故选：B．

2．如图，△ABC中，点D，E在边BC上，∠ABC的平分线垂直AE，垂足为点N，∠ACB的平分线垂直AD，垂足为点M，连接MN．若BC＝7，MN＝，则△ABC的周长为（　　）

A．17 B．18 C．19 D．20
【分析】利用ASA定理证明△BNA≌△BNE，根据全等三角形的性质得到BE＝BA，AN＝NE，同理得到CD＝CA，AM＝MD，根据三角形中位线定理求出DE，根据三角形的周长公式计算，得到答案．
【解答】解：在△BNA和△BNE中，
，
∴△BNA≌△BNE（ASA），
∴BE＝BA，AN＝NE，
同理，CD＝CA，AM＝MD，
∵AM＝MD，AN＝NE，MN＝，
∴DE＝2MN＝3，
∵BE+CD﹣BC＝DE，
∴AB+AC＝BC+DE＝10，
∴△ABC的周长＝AB+AC+BC＝10+7＝17，
故选：A．
3．如图，△ABC的面积是16，点D、E、F、G分别是BC、AD、BE、CE的中点，则△AFG的面积是（　　）

A．6 B．7 C．8 D．9
【分析】根据中线的性质，可得：△AEF的面积＝×△ABE的面积＝×△ABD的面积＝×△ABC的面积＝2，△AEG的面积＝2，根据三角形中位线的性质可得△EFG的面积＝×△BCE的面积＝2，进而得到△AFG的面积．
【解答】解：∵点D是BC的中点，
∴AD是△ABC的中线，
∴△ABD的面积＝△ADC的面积＝×△ABC的面积，
同理得：△AEF的面积＝×△ABE的面积＝×△ABD的面积＝×△ABC的面积＝×16＝2，
△AEG的面积＝2，
△BCE的面积＝×△ABC的面积＝8，
又∵FG是△BCE的中位线，
∴△EFG的面积＝×△BCE的面积＝×8＝2，
∴△AFG的面积是2×3＝6，
故选：A．
4．如图，在△ABC中，∠A＝90°，AC＞AB＞4，点D、E分别在边AB、AC上，BD＝4，CE＝3，取DE、BC的中点M、N，线段MN的长为（　　）

A．2.5 B．3 C．4 D．5
【分析】如图，作CH∥AB，连接DN，延长DN交CH于H，连接EH，首先证明CH＝BD，∠ECH＝90°，解直角三角形求出EH，利用三角形中位线定理即可解决问题．
【解答】解：作CH∥AB，连接DN并延长交CH于H，连接EH，
∵BD∥CH，
∴∠B＝∠NCH，∠ECH+∠A＝180°，
∵∠A＝90°，
∴∠ECH＝∠A＝90°，
在△DNB和△HNC中，
，
∴△DNB≌△HNC（ASA），
∴CH＝BD＝4，DN＝NH，
在Rt△CEH中，CH＝4，CE＝3，
∴EH＝＝＝5，
∵DM＝ME，DN＝NH，
∴MN＝EH＝2.5，
故选：A．

5．如图，DE是△ABC的中位线，∠ABC的角平分线交DE于点F，AB＝8，BC＝12，则EF的长为（　　）

A．1 B．1.5 C．2 D．2.5
【分析】延长AF交BC于H，由三角形中位线定理得到DE∥BC，DE＝BC＝6，AF＝FH，再证△BFA≌△BFH（AAS），得BH＝AB＝8，然后由三角形中位线定理得DF＝4，求解即可．
【解答】解：连接AF并延长交BC于H，如图所示：

∵点D、E分别为边AB、AC的中点，
∴DE∥BC，DE＝BC＝6，AF＝FH，
在△BFA和△BFH中，
，
∴△BFA≌△BFH（AAS），
∴BH＝AB＝8，
∵AD＝DB，AF＝FH，
∴DF是△ABH的中位线，
∴DF＝BH＝4，
∴EF＝DE﹣DF＝2，
故选：C．
解法二：
∵DE是△ABC的中位线，AB＝8，BC＝12，
∴BD＝AB＝4，DE∥BC，DE＝BC＝6，
∴∠DFB＝∠CBF，
∵BF是∠ABC的平分线，
∴∠DBF＝∠CBF，
∴∠DFB＝∠DBF，
∴DF＝BD＝4，
∴EF＝DE﹣DF＝6﹣4＝2，
故选：C．
6．如图，在△ABC中，D是BC边的中点，AE是∠BAC的角平分线，AE⊥CE于点E，连接DE．若AB＝7，DE＝1，则AC的长度是（　　）

A．4 B．4.5 C．5 D．5.5
【分析】延长CE，交AB于点F，通过ASA证明△EAF≌△EAC，根据全等三角形的性质得到AF＝AC，EF＝EC，根据三角形中位线定理得出BF＝2，即可得出结果．
【解答】解：延长CE，交AB于点F．

∵AE平分∠BAC，AE⊥CE，
∴∠EAF＝∠EAC，∠AEF＝∠AEC，
在△EAF与△EAC中，
，
∴△EAF≌△EAC（ASA），
∴AF＝AC，EF＝EC，
又∵D是BC中点，
∴BD＝CD，
∴DE是△BCF的中位线，
∴BF＝2DE＝2．
∴AC＝AF＝AB﹣BF＝7﹣2＝5；
故选：C．
7．如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，点N是BC边上一点，点M为AB边上的动点，点D、E分别为CN，MN的中点，则DE的最小值是（　　）

A．2 B． C．3 D．
【分析】连接CM，当CM⊥AB时，DM的值最小（垂线段最短），此时DE有最小值，根据勾股定理求出AB，根据三角形的面积公式求出CM，根据三角形的中位线得出DE＝CM即可．
【解答】解：连接CM，当CM⊥AB时，CM的值最小（垂线段最短），此时DE有最小值，

理由是：∵∠C＝90°，AC＝6，BC＝8，
∴AB＝＝＝10，
∴AC•BC＝，
∴＝，
∴CM＝，
∵点D、E分别为CN，MN的中点，
∴DE＝CM＝＝，
即DE的最小值是，
故选：B．
8．如图，AB∥CD，AC、BD相交于P，E、F分别为AC、BD的中点，若AB＝10，CD＝6，则EF的长是（　　）

A．1 B．2 C．3 D．4
【分析】连接CF并延长，交AB于G，证明△DFC≌△BFG，根据全等三角形的性质得到BG＝CD＝6，CF＝FG，进而求出AG，根据三角形中位线定理定理计算即可．
【解答】解：连接CF并延长，交AB于G，
∵AB∥DC，
∴∠D＝∠B，
∵F为BD的中点，
∴DF＝BF，
在△DFC和△BFG中，
，
∴△DFC≌△BFG（ASA），
∴BG＝CD＝6，CF＝FG，
∴AG＝AB﹣BG＝4，
∵CF＝FG，CE＝EA，
∴EF＝AG＝×4＝2，
故选：B．

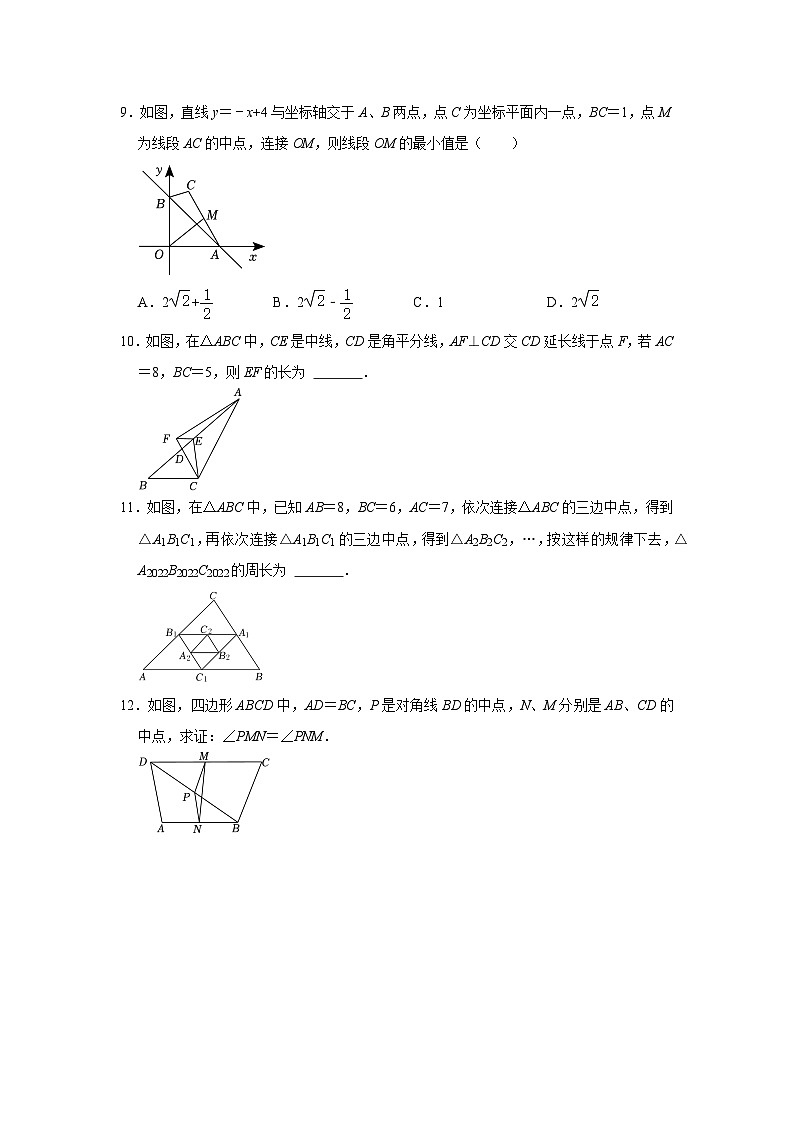
9．如图，直线y＝﹣x+4与坐标轴交于A、B两点，点C为坐标平面内一点，BC＝1，点M为线段AC的中点，连接OM，则线段OM的最小值是（　　）

A．2+ B．2﹣ C．1 D．2
【分析】根据同圆的半径相等可知：点C在半径为1的⊙B上，通过画图可知，C在BD与圆B的交点时，OM最小，在DB的延长线上时，OM最大，根据三角形的中位线定理可得结论．
【解答】解：如图，∵直线y＝﹣x+4与坐标轴交于A，B两点，
∴A（4，0），B（0，4），
∴OA＝OB＝4，
∵点C为坐标平面内一点，BC＝1，
∴C在⊙B上，且半径为1，
取OD＝OA＝4，连接CD，

∵AM＝CM，OD＝OA，
∴OM是△ACD的中位线，
∴OM＝CD，
当OM最小时，即CD最小，而D，B，C三点共线时，当C在线段DB上时，OM最小，
∵OB＝OD＝4，∠BOD＝90°，
∴BD＝4，
∴CD＝4﹣1，
∴OM＝CD＝2﹣，即OM的最小值为＝2﹣，
故选：B．
10．如图，在△ABC中，CE是中线，CD是角平分线，AF⊥CD交CD延长线于点F，若AC＝8，BC＝5，则EF的长为 　1.5　．

【分析】延长AF，CB交于点G，证明△ACF≌△GCF（ ASA），得到CG＝AC＝8，AF＝FG，求出BG，再根据三角形中位线定理解答即可．
【解答】解：如图，延长AF，CB交于点G，

∵CD是△ABC的角平分线，
∴∠ACF＝∠GCF，
∵AF⊥CD，
∴∠AFC＝∠GFC＝90°，
在△ACF和△GCF中，
，
∴△ACF≌△GCF（ ASA），
∴CG＝AC＝8，AF＝FG，
∴BG＝CG﹣CB＝8﹣5＝3，
∵AE＝EB，AF＝FG，
∴EF为△ABG的中位线，
∴，
故答案为：1.5．
11．如图，在△ABC中，已知AB＝8，BC＝6，AC＝7，依次连接△ABC的三边中点，得到△A1B1C1，再依次连接△A1B1C1的三边中点，得到△A2B2C2，…，按这样的规律下去，△A2022B2022C2022的周长为 　　．

【分析】根据三角形中位线定理得到A1B1＝AB，A1C1＝AC，B1C1＝BC，总结规律，根据规律解答即可
【解答】解：∵A1、B1、C1分别为BC、AC、AB的中点，
∴A1B1＝AB，A1C1＝AC，B1C1＝BC，
∴△A1B1C1的周长＝×△ABC的周长＝×21，
……
∴△A2022B2022C2022的周长＝×21，
故答案为：．
12．如图，四边形ABCD中，AD＝BC，P是对角线BD的中点，N、M分别是AB、CD的中点，求证：∠PMN＝∠PNM．

【分析】先说明PN是△DBC的中位线得到PN＝BC，同理可得PM＝AD，进而得到PN＝PM，最后根据等腰三角形的性质即可证明结论．
【解答】解：∵P是对角线BD的中点，N分别是AB的中点，
∴PN是△DBC的中位线，
∴PN＝BC，
同理：PM＝AD，
∵AD＝BC，
∴PN＝PM，
∴∠PMN＝∠PNM．
类型二 三角形中位线在四边形中的应用
【知识点睛】
四边形中中位线的构造
（1） 四边形边上有中点时，取其对角线中点构造三角形中位线;
（2） 四边形对角线上有中点时，取边的中点构造三角形中位线.
此类中位线的构造常出现在等对边四边形或等对角线四边形题目中，用于判断线段关系或由线段引发的角度关系。
注意∶构造出的中位线往往是相等的，且正好是等对边或等对角线的一半.
【类题训练】
1．如图所示，已知四边形ABCD，R、P分别是DC、BC上的点，点E、F分别是AP、RP的中点，当点P在边BC上从点B向点C移动，且点R从点D向点C移动时，那么下列结论成立的是（　　）
A．线段EF的长逐渐增大
B．线段EF的长逐渐减少
C．线段EF的长不变
D．△ABP和△CRP的面积和不变
【分析】连接AR，根据三角形的中位线定理可得EF＝AR，根据AR的变化情况即可判断．
【解答】解：连接AR，
∵E，F分别是AP，RP的中点，
∴EF＝AR，
∵当点P在BC上从点C向点B移动，点R从点D向点C移动时，AR的长度逐渐增大，
∴线段EF的长逐渐增大．
S△ABP+S△CRP＝BC•（AB+CR）．
∵CR随着点R的运动而减小，
∴△ABP和△CRP的面积和逐渐减小．
观察选项，只有选项A符合题意．
故选：A．
2．如图，四边形ABCD中，AD＝BC，点P是对角线BD的中点，E、F分别是AB、CD的中点，若∠EPF＝130°，则∠PEF的度数为（　　）

A．25° B．30° C．35° D．50°
【分析】根据三角形中位线定理得到PF＝BC，PE＝AD，进而证明PF＝PE，根据等腰三角形的性质、三角形内角和定理计算，得到答案．
【解答】解：∵P、F分别是BD、CD的中点，
∴PF＝BC，
同理可得：PE＝AD，
∵AD＝BC，
∴PF＝PE，
∵∠EPF＝130°，
∴∠PEF＝∠PFE＝×（180°﹣130°）＝25°，
故选：A．
3．如图，四边形ABCD中，AD∥BC，AD＝2，BC＝5，点E，F分别是对角线AC，BD的中点，则EF的长为（　　）

A．1 B．1.5 C．2.5 D．3.5
【分析】延长FE交CD于点G，由点E，F分别是对角线AC，BD的中点，从而得FG是△BCD的中位线，则有FG＝2.5，再由AD∥BC，则有FG∥AD，EG是△ACD的中位线，则有EG＝1，从而可求EF的长．
【解答】解：∵取DC中点G，连结FG、EG，如图所示：
∵点E，F分别是对角线AC，BD的中点，
∴FG∥BC，EG∥AD，
∵AD∥BC，
∴EG∥BC，FG∥EG，
∴E、F、G三点共线，
∴FG是△BCD的中位线，
∴FG＝BC＝2.5，
∵AD∥BC，
∴EG∥AD，
∴EG是△ACD的中位线，
∴EG＝AD＝1，
∴EF＝FG﹣EG＝1.5．
故选：B．
4．如图，四边形ABCD中，E，F分别是边AB，CD的中点，则AD，BC和EF的关系是（　　）

A．AD+BC＞2EF B．AD+BC≥2EF C．AD+BC＜2EF D．AD+BC≤2EF
【分析】取AC的中点G，连接EF，EG，GF，根据三角形中位线定理求出EG＝BC，GF＝AD，再利用三角形三边关系：两边之和大于第三边，即可得出AD，BC和EF的关系．
【解答】解：如图，取AC的中点G，连接EF，EG，GF，
∵E，F分别是边AB，CD的中点，
∴EG，GF分别是△ABC和△ACD的中位线，
∴EG＝BC，GF＝AD，
在△EGF中，由三角形三边关系得EG+GF＞EF，即BC+AD＞EF，
∴AD+BC＞2EF，
当AD∥BC时，点E、F、G在同一条直线上，
∴AD+BC＝2EF，
所以四边形ABCD中，E，F分别是边AB，CD的中点，则AD，BC和EF的关系是AD+BC≥2EF．
故选：B．
5．如图，在△ABC中，∠A＝90°，AC＞AB＞4，点D、E分别在边AB、AC上，BD＝4，CE＝3，取DE、BC的中点M、N，线段MN的长为（　　）

A．2.5 B．3 C．4 D．5
【分析】如图，作CH∥AB，连接DN，延长DN交CH于H，连接EH，首先证明CH＝BD，∠ECH＝90°，解直角三角形求出EH，利用三角形中位线定理即可解决问题．
【解答】解：作CH∥AB，连接DN并延长交CH于H，连接EH，
∵BD∥CH，
∴∠B＝∠NCH，∠ECH+∠A＝180°，
∵∠A＝90°，
∴∠ECH＝∠A＝90°，
在△DNB和△HNC中，
，
∴△DNB≌△HNC（ASA），
∴CH＝BD＝4，DN＝NH，
在Rt△CEH中，CH＝4，CE＝3，
∴EH＝＝＝5，
∵DM＝ME，DN＝NH，
∴MN＝EH＝2.5，
故选：A．
6．如图，在四边形ABCD中，∠A＝90°，AB＝4，M，N分别是边BC，AB上的动点（含端点，但点M不与点B重合）点E，F分别是线段DM，MN的中点，若线段EF的最大值为2.5，则AD的长为（　　）

A．5 B． C．2.5 D．3
【分析】根据三角形的中位线定理得出EF＝DN，从而可知DN最大时，EF的最大值为2.5，因为N与B重合时DN最大，此时根据勾股定理求得DN＝DB．
【解答】解：∵点E，F分别是线段DM，MN的中点，
∴ED＝EM，MF＝FN，
∴EF＝DN，
∴DN最大时，EF最大，
∵线段EF的最大值为2.5，
∴DN＝2EF＝5．
∵N与B重合时DN最大，
此时DN＝DB＝＝＝5，
∴AD＝3．
故选：D．
7．如图，四边形ABCD中，∠B＝90°，AB＝8，BC＝6，点M是对角线AC的中点，点N是AD边的中点，连结BM，MN，若BM＝3MN，则线段CD的长是（　　）

A． B．3 C． D．5
【分析】首先由勾股定理求得AC的长度，结合直角三角形斜边上中线的性质得到BM＝AC，三角形中位线定理得到CD＝2MN．
【解答】解：如图，在直角△ABC中，∠B＝90°，AB＝8，BC＝6，则由勾股定理知，AC＝＝＝10．
∵点N是AD边的中点，
∴BM＝AC＝5．
∵BM＝3MN，
∴MN＝BM＝．
∵点M是对角线AC的中点，点N是AD边的中点，
∴MN是△ACD的中位线．
∵CD＝2MN＝2×＝．
故选：C．
8．如图所示，在四边形ABCD中，AB＝CD＝4，M、N、P分别是AD、BC、BD的中点，∠ABD＝20°，∠BDC＝80°，则MN的长是　 　．

【分析】作PH⊥MN于H，根据三角形中位线定理求出PM、PN、∠MPN，根据等腰三角形的性质、勾股定理计算即可．
【解答】解：作PH⊥MN于H，
∵M、N、P分别是AD、BC、BD的中点，
∴PM＝AB＝2，PN＝CD＝2，PM∥AB，PN∥CD，
∴∠MPD＝∠ABD＝20°，∠BPN＝∠BDC＝80°，PM＝PN，
∴∠MPN＝120°，
∵PM＝PN，
∴∠PMN＝30°，MH＝HN，
∴PH＝PM＝1，
由勾股定理得，MH＝＝，
∴MN＝2MH＝2，
故答案为：2．
9．如图，在四边形ABDC中，E、F、G、H分别为AB、BC、CD、DA的中点，并且E、F、G、H四点不共线．当AC＝6，BD＝8时，四边形EFGH的周长是　 　．

【分析】根据三角形中位线定理得到FG∥EH，FG＝EH，根据平行四边形的判定定理和周长解答即可．
【解答】解：∵F，G分别为BC，CD的中点，
∴FG＝BD＝4，FG∥BD，
∵E，H分别为AB，DA的中点，
∴EH＝BD＝4，EH∥BD，
∴FG∥EH，FG＝EH，
∴四边形EFGH为平行四边形，
∴EF＝GH＝AC＝3，
∴四边形EFGH的周长＝3+3+4+4＝14，
故答案为：14
10．如图是华师版九年级上册数学教材第80页的第3题．
如图①，在四边形ABCD中，AD＝BC，P是对角线BD的中点，M是DC的中点，N是AB的中点．
求证：∠PMN＝∠PNM
（1）在上边题目的条件下，延长图①中的线段AD交NM的延长线于点E，延长线段BC交NM的延长线于点F，如图②，请先完成图①的证明，再继续证明∠AEN＝∠F．
（2）若（1）中的∠A+∠ABC＝122°，则∠F的大小为 　29°　．

【分析】（1）根据三角形中位线定理得到PM∥BC，PM＝BC，PN∥AD，PN＝AD，得到PM＝PN，根据等腰三角形的性质证明结论；
（2）根据平行线的性质求出∠MPN，根据等腰三角形的性质计算，得到答案．
【解答】（1）证明：∵P是BD的中点，M是DC的中点，
∴PM是△DBC的中位线，
∴PM∥BC，PM＝BC，
∴∠PMN＝∠F，
同理可得：PN∥AD，PN＝AD，
∴∠AEN＝∠PNM，
∵AD＝BC，
∴PM＝PN，
∴∠PMN＝∠PNM，
∴∠AEN＝∠F；
（2）解：∵PM∥BC，
∴∠MPD＝∠FBD，
∵PN∥AD，
∴∠PNB＝∠A，
∴∠MPN＝∠MPD+∠NPD＝∠FBD+∠A+∠DBA＝122°，
∴∠PMN＝（180°﹣122°）＝29°，
∴∠F＝∠PMN＝29°，
故答案为：29°．
11．如图，在四边形ABCD中，E，F分别是AD，BC的中点．
（1）若AB＝10，CD＝24，∠ABD＝30°，∠BDC＝120°，求EF的长．
（2）若∠BDC﹣∠ABD＝90°，求证：AB2+CD2＝4EF2．

【分析】（1）取BD的中点P，连接EP、FP，由三角形中位线定理得PE∥AB，且PE＝5，PF∥CD，且PF＝12，再证∠EPF＝90°，然后由勾股定理即可得出结论；
（2）由三角形中位线定理得PE∥AB，且，PF∥CD，且，再证∠EPF＝90°，然后由勾股定理即可得出结论．
【解答】（1）解：如图，取BD的中点P，连接EP、FP，
∵E，F分别是AD、BC的中点，AB＝10，CD＝24，
∴PE是△ABD的中位线，PF是△BCD的中位线，
∴PE∥AB，且，且，
∴∠EPD＝∠ABD＝30°，∠DPF＝180°﹣∠BDC＝180°﹣120°＝60°，
∴∠EPF＝∠EPD+∠DPF＝90°，
在Rt△EPF中，由勾股定理得：，
即EF的长为13；
（2）证明：由（1）可知，PE是△ABD的中位线，PF是△BCD的中位线，
∴PE∥AB，且，PF∥CD，且，
∴∠EPD＝∠ABD，∠DPF＝180°﹣∠BDC．
∵∠BDC﹣∠ABD＝90°，
∴∠BDC＝90°+∠ABD，
∴∠EPF＝∠EPD+∠DPF＝∠ABD+180°﹣∠BDC＝∠ABD+180°﹣（90°+∠ABD）＝90°，
∴，
∴AB2+CD2＝4EF2．

12．如图，两个等腰Rt△ABC和Rt△CEF，点B在CE上，∠ABC＝∠E＝90°，连接AF，取AF的中点M，连接MB．求证：BM∥CF．

【分析】如图所示，延长AB交CF于点D．根据全等三角形的性质得到AB＝BD，推出BM是△ADF的中位线，于是得到结论．
【解答】证明：如图所示，延长AB交CF于点D．
∵∠ABC＝90°
∴∠CBD＝90°
∵Rt△ABC和Rt△CEF是等腰直角三角形，
∴∠ACB＝∠ECF＝45°，
∵BC＝BC，
∴△ACB≌△DCB（ASA），
∴AB＝BD，
∵点M是AF的中点，
∴AN＝FM，
∴BM是△ADF的中位线，
∴BM∥CF．
类型三 中位线的构造方法总结
（一）. 连接两点构造三角形的中位线
如图，点B为AC上一点，分别以AB，BC为边在AC同侧作等边△ABD和等边△BCE，点P，M，N分别为AC，AD，CE的中点．
（1）求证：PM＝PN；
（2）求∠MPN的度数．

【分析】（1）连接DC和AE，AE交CD于点M，证明△ABE≌△DBC，得到AE＝DC，利用中位线的性质证明PM＝PN；
（2）根据中位线的性质把∠MPA+∠NPC转化成∠MCA+∠MAC，根据∠DMA＝∠MCA+∠MAC可知求出∠DMA度数即可．
【解答】解：（1）连接DC和AE，AE交CD于点M，
在△ABE和△DBC中，

∴△ABE≌△DBC（SAS）．
∴AE＝DC．
∵P为AC中点，N为EC中点，
∴PN＝AE．
同理可得PM＝DC．
所以PM＝PN．
（2）∵P为AC中点，N为EC中点，
∴PN∥AE．
∴∠NPC＝∠EAC．
同理可得∠MPA＝∠DCA
∴∠MPA+∠NPC＝∠EAC+∠DCA．
又∠DQA＝∠EAC+∠DCA，
∴∠MPA+∠NPC＝∠DQA．
∵△ABE≌△DBC，
∴∠QDB＝∠BAQ．
∴∠DQA＝∠DBA＝60°．
∴∠MPA+∠NPC＝60°．
∴∠MPN＝180°﹣60°＝120°．

（二） 利用角平分线和垂直构造中位线
1．如图，在△ABC中，AB＝6，AC＝4，AD，AE分别是角平分线和中线，过点C作CF⊥AD于点F，连接EF，则线段EF的长为（　　）

A．1 B．2 C．4 D．
【分析】延长CF交AB于G，根据等腰三角形的判定和性质得到 AG＝AC＝4，FG＝CF，进而求出BG，根据三角形中位线定理计算即可．
【解答】解：延长CF交AB于G，
∵AD为△ABC的角平分线，CG⊥AD，
∴△ACG是等腰三角形，
∴AG＝AC＝4，FG＝CF，
∴BG＝AB﹣AG＝6﹣4＝2，
∵AE为△ABC的中线，
∴EF是△BCG的中位线，
∴EF＝BG＝1，
故选：A．
2．在△ABC中，点D是AB的中点，CE平分∠ACB，AE⊥CE于点E．
（1）求证：DE∥BC；
（2）若AC＝5，BC＝7，求DE的长．

【分析】（1）根据CE平分∠ACB，AE⊥CE，运用ASA易证明△ACE≌△FCE．根据全等三角形的性质，得AE＝EF，CF＝AC，根据三角形的中位线定理即可得到结论；
（2）根据三角形的中位线定理就可求解．
【解答】解：（1）延长AE交BC于F，
∵CE平分∠ACB，AE⊥CE于点E，
∴∠ACE＝∠FCE，∠AEC＝∠FEC＝90°，
在△ACE和△FCE中，
，
∴△ACE≌△FCE．
∴AE＝EF，
∵点D是AB的中点，
∴AD＝BD，
∴DE是△ABF的中位线．
∴DE∥BC；
（2）∵△ACE≌△FCE，
∴CF＝AC＝5，
∵DE是△ABF的中位线．
∴DE＝BF＝（BC﹣AC）＝（7﹣5）＝1，
故DE的长为1．

（三） 倍长法构造三角形中位线
如图，△ABC、△BEF为等腰直角三角形，∠ABC＝∠BEF＝90°，BA＝BC，EB＝EF，
连接AF、CF，M为AF的中点．
（1）如图1，当A、F、B共线时，求证：ME＝CF；
（2）如图2，当A、F、B不共线时，求证：ME＝CF；
（3）设BC＝2，请直接写出BF+AF+CF的最小值．

【解答】（1）证明：如图1中，延长FE到D，使ED＝EF，连接AD、BD，
∵△BEF为等腰直角三角形，∠BEF＝90°，
∴∠BFE＝45°，BE⊥DF，
∴BE垂直平分DF，
∴∠BDE＝45°，
∴△BDF是等腰直角三角形，
∴BD＝BF，∠DBF＝90°，
在△ABD和△CBF中，
，
∴△ABD≌△CBF（SAS），
∴AD＝CF，
∵M为AF的中点，DE＝EF，
∴ME是△ADF的中位线，
∴ME＝AD，
∴ME＝CF．

（2）证明：如图2中，延长FE到D，使ED＝EF，连接AD、BD，
∵△BEF为等腰直角三角形，∠BEF＝90°，
∴∠BFE＝45°，BE⊥DF，
∴BE垂直平分DF，
∴∠BDE＝45°，
∴△BDF是等腰直角三角形，
∴BD＝BF，∠DBF＝90°，
∵∠CBF+∠ABF＝∠ABC＝90°，
∠ABD+∠ABF＝∠DBF＝90°，
∴∠CBF＝∠ABD，
在△ABD和△CBF中，
，
∴△ABD≌△CBF（SAS），
∴AD＝CF，
∵M为AF的中点，DE＝EF，
∴ME是△ADF的中位线，
∴ME＝AD，
∴ME＝CF．

（3）解：如图3中，以CF为边在CF的右侧作等边△CFM，将△CFB绕点C逆时针旋转60°得到△CME，连接AE，作EH⊥AC于H，在EH上取一点D，使得CD＝DE，连接DC．
∵CF＝FM，FB＝ME，
∴AF+CF+FB＝AF+FM+ME，
∵AE≤AF+FM+ME，
∴当A，F，M，E共线时，AF+FC+BF的值最小，
∵∠ACB＝45°，∠BCE＝60°，
∴∠ACE＝45°+60°＝105°，
∴∠ECH＝75°，
∵∠H＝90°，
∴∠CEH＝15°，
∵DC＝DE，
∴∠DCE＝∠CED＝15°，
∴∠CDH＝∠DCE+∠DEC＝30°
设CH＝a，则DC＝DE＝2a，DH＝a，EH＝a+2a，
在Rt△ECH中，∵EC2＝CH2+EH2，
∴22＝a2+（a+2a）2，
∴a＝＝（负根已经舍弃），
在Rt△AEH中，AH＝2+＝，EH＝，
∴AE＝＝＝+．

（四） 已知一边中点，取另一边中点构造三角形中位线
如图，四边形ABCD的对角线AC，BD相交于点O，AC⊥BD，E，F分别是AB，CD的中点，若AC＝BD＝2，则EF的长是（　　）

A．2 B． C． D．
【分析】取BC的中点G，AD的中点H，连接EG、GF、FH、HE，根据三角形中位线定理分别求出EG、GF，得出四边形EGFH为正方形，根据正方形的性质计算即可．
【解答】解：取BC的中点G，AD的中点H，连接EG、GF、FH、HE，
∵E，G分别是AB，BC的中点，AC＝2
∴EG＝AC＝1，EG∥AC，
同理：FH＝AC，FH∥AC，EG＝AC，GF∥BD，GF＝BD＝1，
∴四边形EGFH为平行四边形，
∵AC＝BD，
∴GE＝GF，
∴平行四边形EGFH为菱形，
∵AC⊥BD，EG∥AC，GF∥BD，
∴EG⊥GF，
∴菱形EGFH为正方形，
∴EF＝EG＝，
故选：D．
（五） 已知两边中点，取第三边中点构造三角形的中位线
已知：如图所示，在△ABC中，AB＝AC，AD是BC边上的高，P是AD的中点，延长BP交AC于点F．
（1）求证：PB＝3PF；
（2）如果AC的长为13，求AF的长．

【分析】（1）本题可通过构建中位线来求解，过D点作DE∥BF，交AC于E；则DE、PF分别是△CBF、△ADE的中位线，可根据BP、PF与DE的比例关系求出BP、PF的比例关系．
（2）由（1）可知：E、F是AC的三等分点，由此可得出AF的长．
【解答】解：（1）证明：如图所示，过D点作DE∥BF，交AC于E，
因为AB＝AC，AD为△ABC的高，
所以根据等腰三角形的三线合一得D为BC的中点，
所以DE＝BF．
同理，因为P为AD的中点
所以PF＝DE，即PF＝BF，所以BP＝3PF．
（2）由（1）得：PF、DE分别是DE、BF的中位线，
∴AF＝EF，CE＝EF．
∴AC＝AF+EF+CE＝3AF．
∵AC＝13，
∴AF＝．