数学人教版8年级上册期中测试AB卷·A基础测试

这是一份数学人教版8年级上册期中测试AB卷·A基础测试，共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
          数学人教版8年级上册  
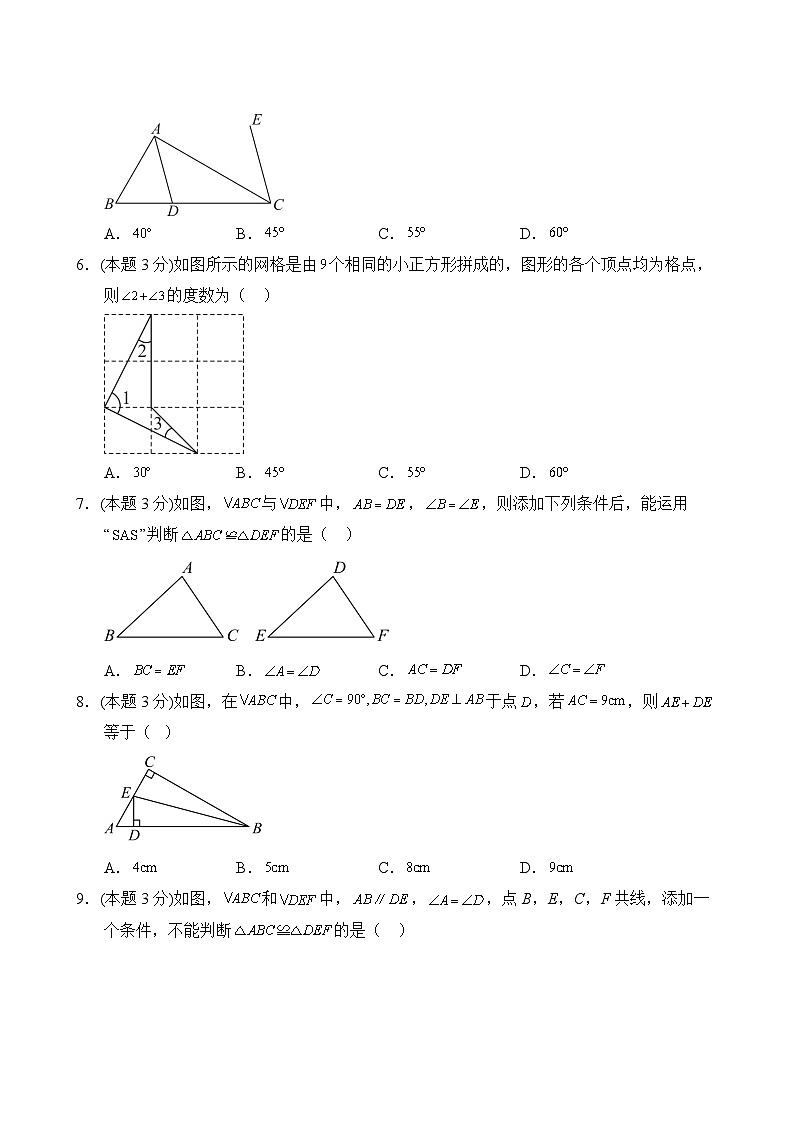
数学人教版8年级上册期中测试AB卷 A基础测试时间：100分钟  满分：120分班级__________姓名__________得分__________一、单选题(共30分)1．(本题3分)如图，菊花1角硬币为外圆内正九边形的边缘异形币，则该正九边形一个内角的大小为（　　）A．135° B．140° C．145° D．150°2．(本题3分)以下列各组线段为边，能组成三角形的是（    ）A． B． C． D．3．(本题3分)如图，已知，，，，，则点到直线的距离等于（    ）A． B． C． D．4．(本题3分)如图，交于，交于，，，等于（   ）A． B． C． D．5．(本题3分)如图，在中，是的平分线，过点的射线与平行，若，，则的度数为（    ）A． B． C． D．6．(本题3分)如图所示的网格是由个相同的小正方形拼成的，图形的各个顶点均为格点，则的度数为（    ）A． B． C． D．7．(本题3分)如图，与中，，，则添加下列条件后，能运用“”判断的是（    ）A． B． C． D．8．(本题3分)如图，在中，于点，若，则等于（   ）  A． B． C． D．9．(本题3分)如图，和中，，，点B，E，C，F共线，添加一个条件，不能判断的是（    ）  A． B． C． D．10．(本题3分)如图，，以点B为圆心，小于的长为半径作圆弧，分别交于点E、F，再分别以E、F为圆心，大于的长为半径作圆弧，两弧交于点G，作射线交于点H．若，则（    ）  A． B． C． D．二、填空题(共15分)11．(本题3分)如图，在中，，，和分别是它的高和角平分线，则________．  12．(本题3分)如图，则___________．  13．(本题3分)如图，在五边形中，，的平分线与的平分线交于点，则______．14．(本题3分)如图，有一个直角三角形，，，，一条线段，、两点分别在和过点且垂直于的射线上运动，问点运动到________位置时，才能使．     15．(本题3分)如图，已知是的角平分线，点，分别是射线，的动点，于且，则线段的最小值是________．  三、解答题(共75分)16．(本题6分)如图，中，，，，，求．    17．(本题7分)如图，已知．(1)画出的中线和角平分线；(2)画出的高，．18．(本题7分)如图，C为上一点．点A，D分别在两侧．，，．(1)证明：；(2)若，求的度数．19．(本题7分)如图，在四边形中，，，点，分别在，上，．  (1)判断与的大小关系，并说明理由．(2)若，平分，求的度数．20．(本题7分)如图，是射线上一点，已知． (1)求证：．(2)若，且平分，求的度数．21．(本题7分)如图，点E，F分别在上，，于点O，，求证：证明：∵（已知），∴（__________），∴（__________），∵（已知），∴（__________），∵（已知），∴__________（__________），∴（等量代换），∴（__________）．22．(本题7分)如图，在中，的平分线交于点D．(1)尺规作图：作的平分线交于点O．（保留作图痕迹，不写作法）(2)求的度数．23．(本题7分)如图，在中，平分，于点E，点F在上，．(1)求证：．(2)若，求的长．24．(本题10分)麒麟某数学兴趣小组的同学用数学知识测一池塘的长度，他们所绘如图，点B，F，C，E在直线上（点F，C之间不能直接测量，为池塘的长度），点A，D在的异侧，且，，测得．(1)求证：；(2)若，，求池塘的长．25．(本题10分)如图：直线是经过顶点C的一条直线，，E、F分别是直线上两点，且．  【数学思考】(1)若直线是经过的内部，且E、F在射线上．请解决下面两个问题：①如图1， ，则 （填或），猜测线段与线段的数量关系，并证明你的猜想；②如图2，若，当与之间满足 时，能够使得①中的结论仍然成立，并证明两个结论．【问题拓展】(2)如图3.若直线经过的外部， ，请直接写出三条线段的数量关系．
参考答案1．B2．A3．C4．A5．B6．B7．A8．D9．B10．C11．/9度12．13．/度14．点15．316．解：∵，∴．∵，，∴．∵，∴，，∴，∴．17．（1）解：即为所求作的中线，为所求作的角平分线，如图所示：（2）解：、为所求作的高线，如图所示：18．（1）证明：∵，∴，在和中，， ∴．（2）∵，∴，∴．19．（1）解：，理由如下：∵，，∴，∴，∴，∵，∴，∴；（2）解：∵平分，∴，∵，∴，∵，，∴．∵，∴，∴．20．（1）证明：，，；（2）解：平分，，，，，，，，．21．解：∵（已知），∴（垂直的定义），∴（直角三角形的两个锐角互余）∵（已知）∴（同角的余角相等）．∵（已知）∴（两直线平行，内错角相等）∴（等量代换）∴（同位角相等，两直线平行）故答案为：垂直的定义；直角三角形的两个锐角互余；同角的余角相等；；两直线平行，内错角相等；同位角相等，两直线平行．22．（1）解：如图，即为所求；（2），，，平分，平分，，，．23．（1）证明：∵平分，于点E，∴．在与中，，∴，∴．（2）解：设，则，∵平分，于点E，∴．在与中，，∴，∴，即，解得，即．24．（1）证明：∵，∴，在与中，∴；（2）解：∵，∴∴，∴，∵，，∴．答：FC的长是．25．（1）①证明：∵∴ ∵∴∴在和中∴  ∴∵∴故答案为：；②证明：∵，，， ∴∵， ∴  ∴∴∴在和中∴  ∴∵∴故答案为：；（2）证明： 与（2）同理可得，∴∵∴．