


初中数学华师大版九年级上册23.4 中位线复习课件ppt
展开1.中线、中位线2.倍长中线题型3.中点四边形题型
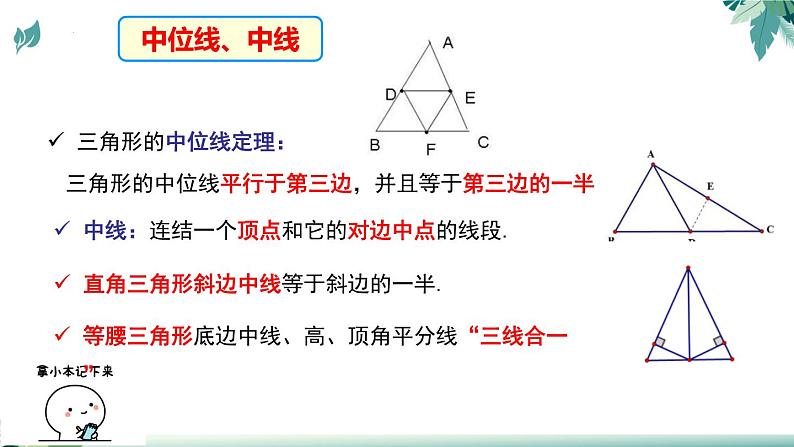
中线:连结一个顶点和它的对边中点的线段.
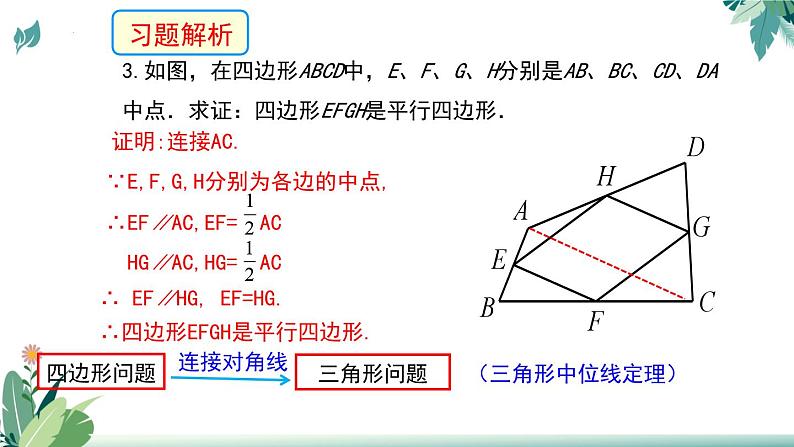
3.如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.求证:四边形EFGH是平行四边形.
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴EF∥AC,EF= AC HG∥AC,HG= AC
∴四边形EFGH是平行四边形.
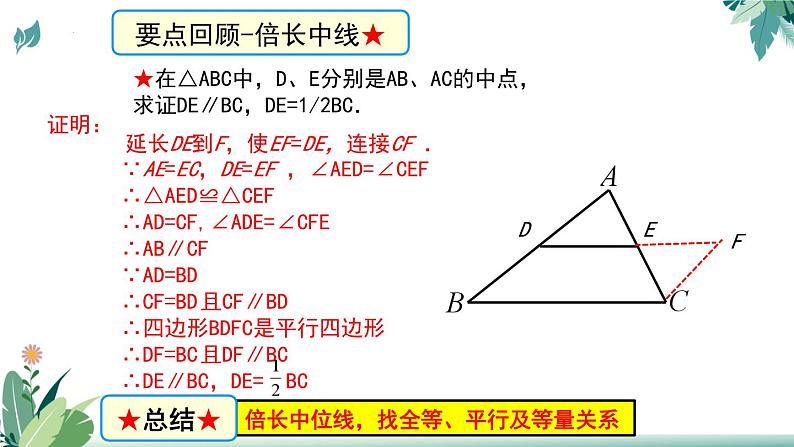
延长DE到F,使EF=DE,连接CF .
∵AE=EC,DE=EF ,∠AED=∠CEF∴△AED≌△CEF∴AD=CF,∠ADE=∠CFE∴AB∥CF∵AD=BD∴CF=BD且CF∥BD∴四边形BDFC是平行四边形∴DF=BC且DF∥BC∴DE∥BC,DE= BC
★在△ABC中,D、E分别是AB、AC的中点,求证DE∥BC,DE=1/2BC.
【练】在△ABC中,AC=5,中线AD=7,则AB边的取值范围( )A 1
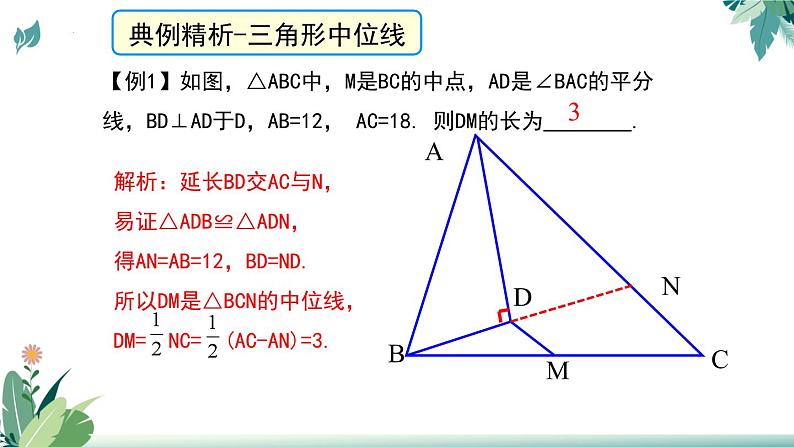
【例1】如图,△ABC中,M是BC的中点,AD是∠BAC的平分线,BD⊥AD于D,AB=12, AC=18. 则DM的长为 .
解析:延长BD交AC与N,易证△ADB≌△ADN,得AN=AB=12,BD=ND.所以DM是△BCN的中位线,DM= NC= (AC-AN)=3.
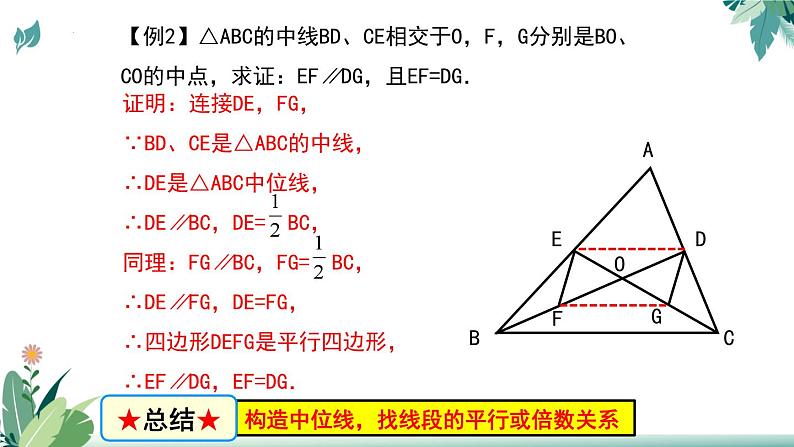
【例2】△ABC的中线BD、CE相交于O,F,G分别是BO、CO的中点,求证:EF∥DG,且EF=DG.
证明:连接DE,FG,∵BD、CE是△ABC的中线,∴DE是△ABC中位线,∴DE∥BC,DE= BC,同理:FG∥BC,FG= BC,∴DE∥FG,DE=FG,∴四边形DEFG是平行四边形,∴EF∥DG,EF=DG.
【例3】如图,AD是△ABC中BC边上的中线,E为AD的中点,延长BE交AC于点F,求证:EF=1/4BF.
证明:过D作DQ∥BF交AC于Q,∵E为AD中点,D为BC中点,DQ∥BF∴EF和DQ分别为△ADQ和△CBF的中位线,∴EF= DQ,DQ= BF∴EF= BF
【例4】已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形。
证明:连接BD,∵E、F、G、H分别是AB、BC、CD、DA的中点,∴HE∥DB,HE= DB ;FG∥DB,FG= DB,∴FG∥HE,GF=HE,∴四边形EFGH是平行四边形.
【例5】如图,△ABC中,AB=AC,D是BC中点,DE⊥AB于E,DF⊥AB于F,求证:DE=DF。
证明:连接AD. ∵AB=AC,D是BC中点 ∴AD平分∠BAC(三线合一)又∵DE⊥AB,DF⊥AB ∴DE=DF(角平分线性质)
【例6】如图,Rt△ABC中,EF是中位线,CD是斜边AB中线,EF=12,则CD=_____。
解析:∵EF是中位线,∴EF= AB ∵CD是Rt△ABC斜边中线, ∴CD= AB,∴CD=EF
【例7】如图,△ABC中,AB=AC,∠ABD=∠CBD,BD⊥DE于D,求证:CD=1/2BE。
证明:如图,取BE的中点F,连接DF,∵BD⊥DE,∴∠BDE=90°,∴DF=EF=BF= BE∴∠BDF=∠CBD∵∠ABD=∠CBD,∴∠DFC=∠ABC=2 ∠CBD又∵AB=AC,∴∠C=∠ABC∴ ∠DFC=∠C,∴CD=DF= BE
【例8】如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.求证:四边形EFGH是平行四边形.
【★探索】a.原四边形ABCD的对角线AC、BD满足________时,四边形EFGH是矩形。b.原四边形ABCD的对角线AC、BD满足________时,四边形EFGH是菱形。c.原四边形ABCD的对角线AC、BD满足________时,四边形EFGH是正方形。
AC⊥BD且AC=BD
矩形判定:一个角是直角的平行四边形
菱形判定:一组领边相等的平行四边形
正方形判定:一组领边相等且有一个角是直角的平行四边形
1. 如图:如果AD= AC,AE= AB,DE=2cm,那么BC= cm.
解析:取AC、AB中点G、H,连接GH 运用两次中位线定理
2.在△ABC中,E、F、G、H分别为AC、CD、 BD、 AB的中点,若AD=3,BC=8,则四边形EFGH的周长是 .
解析:由中位线定理可知 EF=HG= AD EH=FG= BC 四边形EFGH的周长=AD+BC=11
3.在Rt△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,∠B=30°,CE=4,则CD= .
解析:∵CE是Rt△ABC斜边中线,CE=4 ∴AB=8, ∵∠B=30°AB=8,∠ACB=90° 根据勾股定理AC=4 又∵∠ADC=90°,∠A=60° 根据勾股定理CD=
4.在四边形ABCD中,AD=BC,E,F分别是边AB,CD的中点,G为对角线BD的中点.求证:△EFG是等腰三角形.
证明:在△ABD中∵E,G分别是边AB,BD的中点,∴EG= AD,∴同理FG= BC;又∵AD=BC,∴EG=FG,∴△EFG是等腰三角形.
5.如图,在四边形ABCD中,AC⊥BD,BD=12,AC=16,E,F分别为AB,CD的中点,求EF的长.
解:取BC边的中点G,连接EG、FG.∵E,F分别为AB,CD的中点,∴EG是△ABC的中位线,FG是△BCD的中位线,
又∵BD=12,AC=16,AC⊥BD,∴EG=8,FG=6,EG⊥FG,∴在直角△EGF中,由用勾股定理,得EF=10
∴EG∥AC,EG= AC;FG∥BD,FG= BD,
构造出中位线或斜边上的中线
根据中位线的性质或中线的性质
得出平行线和线段间的关系
课堂小结-中点问题解题思路
中点四边形是平行四边形
1.整理本堂课笔记与课后习题一起上交
2. 如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样量出A、B两点间的距离?根据是什么?
华师大版九年级上册23.4 中位线评课课件ppt: 这是一份华师大版九年级上册23.4 中位线评课课件ppt,共17页。PPT课件主要包含了教师释疑,几何语言,能力提升,构建知识体系,方法总结等内容,欢迎下载使用。
数学中考总复习-平行四边形(知识点+中考题型总结)课件: 这是一份数学中考总复习-平行四边形(知识点+中考题型总结)课件,共18页。PPT课件主要包含了加一个内角为90°,加对角线相等,加一个内角为直角,加对角线垂直且相等,加对角线互相垂直,加一组邻边相等,加三个角是直角,加四条边都相等,点到直线的距离等内容,欢迎下载使用。
数学七年级下册9.2 三角形的内角课堂教学ppt课件: 这是一份数学七年级下册9.2 三角形的内角课堂教学ppt课件,共19页。PPT课件主要包含了见习题,答案显示,△ABC△ADF等内容,欢迎下载使用。













