

综合训练03函数的概念与性质(14种题型60题专练)-【一轮复习讲义】2024年高考数学复习全程规划(新高考地区专用)(解析版)
展开
这是一份综合训练03函数的概念与性质(14种题型60题专练)-【一轮复习讲义】2024年高考数学复习全程规划(新高考地区专用)(解析版),共41页。试卷主要包含了函数的定义域为 (0,1] ,=的定义域为R等内容,欢迎下载使用。
综合训练03函数的概念与性质(14种题型60题专练)
一.函数的定义域及其求法(共3小题)
1.(2023•东城区一模)函数的定义域为 (0,1] .
【分析】直接由根式内部的代数式大于等于0,对数式的真数大于0联立取交集即可.
【解答】解:要使有意义,则,解得0<x≤1.
所以原函数的定义域为(0,1].
故答案为(0,1].
【点评】本题考查了函数的定义域及其求法,函数的定义域就是使函数解析式有意义的自变量x的取值范围,是基础题.
2.(2023•湖北模拟)函数的定义域是( )
A.(﹣∞,1) B.(0,+∞) C.(0,1) D.(﹣∞,0]
【分析】利用根式及对数函数的定义建立不等式组,解不等式组得到定义域即可.
【解答】解:由,得,解得x≤0,
所以函数的定义域为(﹣∞,0].
故选:D.
【点评】本题主要考查了函数定义域的求解,属于基础题.
3.(2023•泸县校级模拟)已知函数f(x)=的定义域为R.
(1)求实数m的范围;
(2)若m的最大值为n,当正数a,b满足+=n时,求4a+7b的最小值.
【分析】(1)利用绝对值不等式的性质即可得出;
(2)利用柯西不等式的性质即可得出.
【解答】解:(1)∵函数的定义域为R,∴|x+2|+|x﹣4|﹣m≥0在R上恒成立,即m≤(|x+2|+|x﹣4|)min,
∴|x+2|+|x﹣4|≥|(x+2)﹣(x﹣4)|=6,∴m≤6;
(2)由(1)知n=6,4a+7b=(4a+7b)(+)=[(a+5b)+(3a+2b)](+)≥,
当且仅当a=,b=时取等号,
∴4a+7b的最小值为.
【点评】本题考查了绝对值不等式的性质、函数的定义域,考查了推理能力与计算能力,属于中档题.
二.函数的值域(共7小题)
4.(2023•全国模拟)世界公认的三大著名数学家为阿基米德、牛顿、高斯,其中享有“数学王子”美誉的高斯提出了取整函数y=[x],[x]表示不超过x的最大整数,例如[1.1]=1,[﹣1.1]=﹣2.已知,,则函数f(x)的值域为( )
A.{4,6,8} B.{4,5,6} C.{4,5,6,7,8} D.{4,8}
【分析】根据函数的单调性先求出函数的值域,再由已知定义可求.
【解答】解:易知,在上单调递减,[2,6)上单调递增.
当x=2时,;当时,;当x=6时,,
所以,则函数f(x)的值域为{4,5,6,7,8}.
故选:C.
【点评】本题以新定义为载体,主要考查了函数单调性在函数最值求解中的应用,属于基础题.
5.(2023•沈阳三模)已知函数,若f(x)的值域是R,则实数a的取值范围是( )
A.(﹣∞,0] B.[0,1] C.[0,+∞) D.(﹣∞,1]
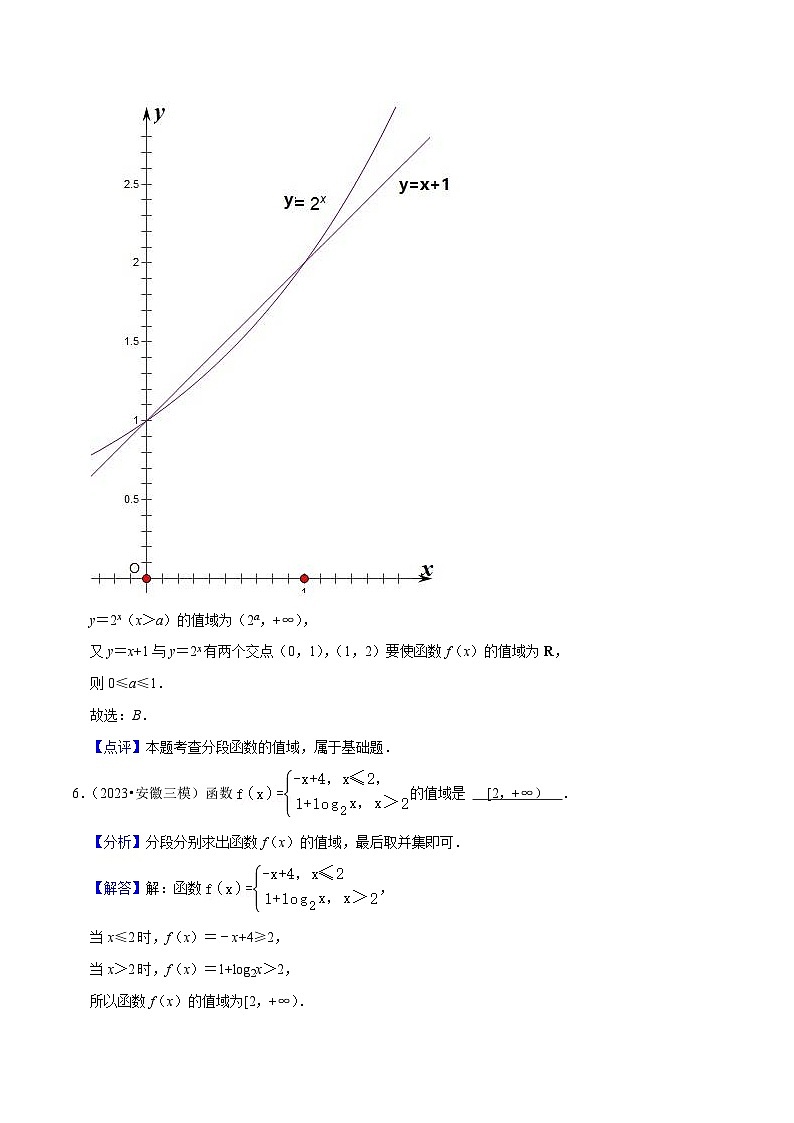
【分析】y=x+1与y=2x有两个交点(0,1),(1,2),结合图象可确定实数a的取值范围.
【解答】解:函数y=x+1在(﹣∞,a]上为增函数,值域为(﹣∞,a+1],如图:
y=2x(x>a)的值域为(2a,+∞),
又y=x+1与y=2x有两个交点(0,1),(1,2)要使函数f(x)的值域为R,
则0≤a≤1.
故选:B.
【点评】本题考查分段函数的值域,属于基础题.
6.(2023•安徽三模)函数的值域是 [2,+∞) .
【分析】分段分别求出函数f(x)的值域,最后取并集即可.
【解答】解:函数,
当x≤2时,f(x)=﹣x+4≥2,
当x>2时,f(x)=1+log2x>2,
所以函数f(x)的值域为[2,+∞).
故答案为:[2,+∞).
【点评】本题主要考查了求函数的值域,属于基础题.
7.(2023•虹口区二模)对于定义在R上的奇函数y=f(x),当x>0时,,则该函数的值域为 (﹣∞,﹣5]∪{0}∪[5,+∞) .
【分析】根据奇函数的性质求得f(0)=0,再结合基本不等式求x>0时y=f(x)的取值范围,再结合奇函数的性质求x<0时函数值的范围,由此可得函数值域.
【解答】解:因为y=f(x)为R上的奇函数
所以f(﹣x)=﹣f(x),所以f(0)=0,
又当x>0时,2x+1>2,
所以=2x+1+﹣1≥2﹣1=5,
当且仅当x=1时等号成立,
即当x>0时,f(x)≥5,
因为y=f(x)为R上的奇函数,
所以函数y=f(x)的图象关于原点对称,所以x<0时,f(x)≤﹣5,
所以函数y=f(x)的值域为(﹣∞,﹣5]∪{0}∪[5,+∞).
故答案为:(﹣∞,﹣5]∪{0}∪[5,+∞).
【点评】本题考查函数的值域和奇偶性,属于基础题.
8.(2023•南部县校级模拟)设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若对任意x∈[a,b],都有|f(x)﹣g(x)|≤1成立,则称f(x)和g(x)在[a,b]上是“亲密函数”,区间[a,b]称为“亲密区间”.若f(x)=x2﹣3x+4与g(x)=2x﹣1在[a,b]上是“亲密函数”,则b﹣a的最大值是 1 .
【分析】根据新定义先解出亲密区间[a,b],即可得出答案.
【解答】解:由|f(x)﹣g(x)|=|x2﹣5x+5|≤1,得﹣1≤x2﹣5x+5≤1,解得1≤x≤2或3≤x≤4.
∴f(x)=x2﹣3x+4与g(x)=2x﹣1在[1,2]或[3,4]上是“亲密函数”,
则b﹣a的最大值是1.
故答案为1.
【点评】正确理解新定义是解题的关键.
(多选)9.(2023•广州二模)已知函数的定义域是[a,b](a,b∈Z),值域为[0,1],则满足条件的整数对(a,b)可以是( )
A.(﹣2,0) B.(﹣1,1) C.(0,2) D.(﹣1,2)
【分析】可设,该函数在(0,2]上单调递减,在[﹣2,0)上单调递增,从而得出f(x)在(0,2]和[﹣2,0)上的单调性及值域,并得出f(0)=1,从而得出f(x)在[﹣2,0],[0,2],[﹣1,2]上的值域都是[0,1],从而得出a,b的可能取值.
【解答】解:x≠0时,设,g(x)在(0,2]上单调递减,在[﹣2,0)上单调递增,且,
∴f(x)在(0,2]上单调递减,0≤f(x)<1;f(x)在[﹣2,0)上单调递增,0≤f(x)<1,且f(0)=1,
∴f(x)在[0,2],[﹣2,0],[﹣1,2]上的值域为[0,1],a,b中至少一个取﹣2或2,
∴整数对(a,b)可以是(﹣2,0),(0,2),(﹣1,2).
故选:ACD.
【点评】本题考查了函数的单调性,函数的单调性,根据函数单调性求函数值域的方法,函数单调性的定义,考查了计算能力,属于中档题.
10.(2023•全国二模)已知函数f(x)=4x﹣2x+2﹣1,x∈[0,3],则其值域为 [﹣5,31] .
【分析】令t=2x,将问题转化为求二次函数在区间[1,8]上的值域问题,结合二次函数单调性,即可求解.
【解答】解:令t=2x,
∵x∈[0,3],
∴1≤t≤8,
∴g(t)=t2﹣4t﹣1=(t﹣2)2﹣5,t∈[1,8]
又y=g(t)关于t=2对称,开口向上,所以g(t)在[1,2)上单调递减,在(2,8]上单调递增,
且|8﹣2|>|2﹣1|,
∴t=2时,函数取得最小值,即g(t)min=﹣5,t=8时,函数取得最大值,即g(t)max=31,
∴f(x)∈[﹣5,31].
故答案为:[﹣5,31].
【点评】本题主要考查了指数函数及二次函数性质的应用,还考查了换元法的应用,属于中档题.
三.函数解析式的求解及常用方法(共4小题)
11.(2023•沙坪坝区校级模拟)已知函数f(x)=x﹣,则如图所对应的函数的解析式为( )
A.y=f(|x+1|) B.y=f(|x|﹣1) C.y=f(|x|+1) D.y=|f(x+1)|
【分析】根据图象的对称性,定义域看确定选项.
【解答】解:函数图象关于y轴对称,为偶函数,则排除A,D选项,
从图象上观察,x∈R,
B项,y=f(|x|﹣1)=|x|﹣1﹣,x≠±1,与图象不符,
C项,y=f(|x|+1)是偶函数,且x∈R.
故选:C.
【点评】本题考查函数的图象,函数的性质,属于基础题.
12.(2023•浙江模拟)定义在R上的非常数函数f(x)满足:f(﹣x)=f(x),且f(2﹣x)+f(x)=0.请写出符合条件的一个函数的解析式f(x)= (答案不唯一) .
【分析】根据已知f(﹣x)=f(x),且f(2﹣x)+f(x)=0得出对称轴和对称中心,确定一个具体函数即可.
【解答】解:因为f(2﹣x)+f(x)=0.得出对称中心(1,0),且f(﹣x)=f(x)得出对称轴为y轴,
所以周期为4的函数都可以.
故答案为:(答案不唯一).
【点评】本题主要考查了函数的对称性和周期性,属于基础题.
(多选)13.(2023•全国模拟)已知函数f(x)满足:2f2(x)+3f2(2﹣x)=5x4﹣16x3+48x2﹣64x+32,则以下不正确的有( )
A.f(0)=4 B.f(x)对称轴为x=4
C.f(2)=3 D.f(7)=25
【分析】变形给定等式,求出函数f(x)的解析式,再逐项分析判断作答.
【解答】解:因为5x4﹣16x3+48x2﹣64x+32=2(x4﹣8x3+24x2﹣32x+16)+3x4
=2[(x4﹣8x3+16x2)+8(x2﹣4x)+16]+3x4=2[(x2﹣4x)+8(x2﹣4x)+16]+3x4
=2(x2﹣4x+4)+3x4=2(x﹣2)4+3x4,
于是2f2(x)+3f2(2﹣x)=2(x﹣2)4+3x4,
可得2f2(2﹣x)+3f2(x)=2x4+3(2﹣x)4,
两式联立解得f(x)=(x﹣2)2,f(2﹣x)=x2,
因此f(x)=(x﹣2)2,f(0)=4,f(7)=25,AD正确;
函数f(x)图象的对称轴为x=2,f(2)=0,BC错误.
故选:BC.
【点评】本题主要考查了求函数解析式,属于中档题.
14.(2023•历城区校级二模)若函数,,则f(x)+g(x)= .
【分析】先求出函数的定义域,然后结合函数定义域即可求解.
【解答】解:∵,
由﹣(x﹣1)2≥0,得(x﹣1)2≤0得x﹣1=0,
解得x=1,
即函数的定义域为{1},
∵,
∴x2+3x﹣2≥0,
解得或,
∴函数的定义域为,
故函数f(x)+g(x)的定义域为{1},
∴,x∈{1}.
故答案为:.
【点评】本题主要考查函数值的计算,根据条件先求出函数的定义域是解决本题的关键,是中档题.
四.函数的图象与图象的变换(共4小题)
15.(2023•南开区二模)已知函数f(x)=ln|x|﹣ex,则f(x)的图象大致为( )
A. B.
C. D.
【分析】求出f(1)<0,可排除A,B,C,即可得出答案.
【解答】解:当x=1时,f(1)=ln1﹣e=﹣e<0,排除A,B,C.
故选:D.
【点评】本题主要考查了函数图象的变换,属于基础题.
16.(2022•甲卷)函数f(x)=(3x﹣3﹣x)cosx在区间[﹣,]的图像大致为( )
A.
B.
C.
D.
【分析】判断函数的奇偶性,结合函数的特殊值判断点的位置,推出选项即可.
【解答】解:f(x)=(3x﹣3﹣x)cosx,
可知f(﹣x)=(3﹣x﹣3x)cos(﹣x)=﹣(3x﹣3﹣x)cosx=﹣f(x),
函数是奇函数,排除BD;
当x=1时,f(1)=(3﹣3﹣1)cos1>0,排除C.
故选:A.
【点评】本题考查函数的奇偶性以及函数的图象的判断,是中档题.
17.(2022•甲卷)函数y=(3x﹣3﹣x)cosx在区间[﹣,]的图像大致为( )
A.
B.
C.
D.
【分析】判断函数的奇偶性,结合函数的特殊值判断点的位置,推出选项即可.
【解答】解:f(x)=(3x﹣3﹣x)cosx,
可知f(﹣x)=(3﹣x﹣3x)cos(﹣x)=﹣(3x﹣3﹣x)cosx=﹣f(x),
函数是奇函数,排除BD;
当x=1时,f(1)=(3﹣3﹣1)cos1>0,排除C.
故选:A.
【点评】本题考查函数的奇偶性以及函数的图象的判断,是中档题.
18.(2022•乙卷)如图是下列四个函数中的某个函数在区间[﹣3,3]的大致图像,则该函数是( )
A.y= B.y=
C.y= D.y=
【分析】首先分析函数奇偶性,然后观察函数图像在(1,3)存在零点,可排除B选项,再利用基本不等式可判断CD选项错误.
【解答】解:首先根据图像判断函数为奇函数,
其次观察函数在(1,3)存在零点,
而对于B选项:令y=0,即,解得x=0,或x=1或x=﹣1,故排除B选项;
C选项:当x>0时,2x>0,x2+1>0,因为cosx∈[﹣1,1],
故=,且当x>0时,,故,
而观察图像可知当x>0时,f(x)max≥1,故C选项错误.
D选项,y=中,当x=3时,y=>0,故排除D选项.
故选:A.
【点评】本题主要考查函数图像的识别,属于基础题.
五.函数单调性的性质与判断(共3小题)
19.(2022•全国)设函数f(x)=ax(a>0,且a≠1)是增函数,若=,则a= 3 .
【分析】先利用指数幂的运算化简求出a,再利用指数函数的单调性求解即可.
【解答】解:∵函数f(x)=ax(a>0,且a≠1),
∴===,
∴3a2﹣10a+3=0,
∴a=3或a=,
∵函数f(x)=ax(a>0,且a≠1)是增函数,
∴a=3,
故答案为:3.
【点评】本题考查指数函数的单调性和指数幂的运算,属于基础题.
20.(2023•石家庄三模)已知函数f(x)同时满足性质:①f(﹣x)=﹣f(x);②对于∀x1,x2∈(0,1),,则函数f(x)可能是( )
A.f(x)=ex﹣e﹣x B.
C.f(x)=sin4x D.f(x)=x2
【分析】由函数奇偶性和单调性的定义进行辨析即可.
【解答】解:由函数奇偶性的定义,若函数f(x)满足f(﹣x)=﹣f(x),则函数f(x)为奇函数,
由函数单调性的定义,若函数f(x)满足∀x1,x2∈(0,1),,则函数f(x)在区间(0,1)上单调递增,
选项中四个函数定义域均为R,∀x∈R,都有﹣x∈R,
对于A,f(﹣x)=e﹣x﹣ex=﹣(ex﹣e﹣x)=﹣f(x),故f(x)为奇函数,满足性质①,f(x)=ex﹣e﹣x在R上单调递增,满足性质②;
对于B,由指数函数的性质,为非奇非偶函数,在R上单调递减,性质①,②均不满足;
对于C,f(﹣x)=sin(﹣4x)=﹣sin4x=﹣f(x),故f(x)为奇函数,满足性质①,
令,k∈Z,解得,k∈Z,
∴f(x)的单调递增区间为,k∈Z,故f(x)在(0,1)不单调,不满足性质②;
对于D,由幂函数的性质,f(x)=x2为偶函数,在区间[0,+∞)单调递增,不满足性质①,满足性质②.
故选:A.
【点评】本题主要考查了函数奇偶性及单调性的判断及应用,属于中档题.
21.(2023•杨浦区校级三模)已知函数,设xi(i=1、2、3)为实数,且x1+x2+x3=0,给出下列结论:①若x1•x2•x3>0,则;②若x1•x2•x3<0,则.则( )
A.①正确,②错误 B.①错误,②正确
C.①②都正确 D.①②都错误
【分析】令,得到g(x)为递增函数,且为奇函数,①中,不妨设 x1<0,x2<0,x3>0,结合A(x1+x2,f(x1+x2)),利用直线OA的方程得到g(x1)+g(x2)<g(x1+x2),进而得到g(x1)+g(x2)+g(x3)<0,可判断①正确;②中,不妨设 x1<0,x2>0,x3>0,得到点B(x2+x3,f(x2+x3)),利用直线OB的方程判断②正确.
【解答】解:令函数,
可得函数g(x)为单调递增函数,
又由 ,即g(﹣x)=﹣g(x),
所以函数g(x)为奇函数,图象关于点(0,0)对称,如图(1)所示,
①中,因为 x1+x2+x3=0,且 x1⋅x2⋅x3>0,则 x3=﹣(x1+x2),不妨设 x1<0,x2<0,x3>0,
则点A(x1+x2,f(x1+x2)),此时直线OA的方程为 ,
可得,则 ,
可得g(x1)+g(x2)﹣g(x1+x2)<0,又由 g(x3)=g[﹣(x1+x2)]=﹣g(x1+x2),
所以g(x1)+g(x2)+g(x3)<0,即,
即,所以①正确;
②中,若 x1⋅x2⋅x3<0,不妨设 x1⋅x2⋅x3>0,则x1=﹣(x2+x3),不妨设 x1<0,x2>0,x3>0,
则点B(x2+x3,f(x2+x3)),此时直线OB的方程为,
可得 ,
则,
可得g(x2)+g(x3)﹣g(x2+x3)>0,
又由g(x1)=g[﹣(x2+x3)]=﹣g(x2+x3),
所以g(x1)+g(x2)+g(x3)>0,
即,
即 ,所以②正确.
故选:C.
【点评】本题考查函数的性质,考查直线与函数的综合应用,属于中档题.
六.复合函数的单调性(共3小题)
22.(2023•黄山模拟)“a<1”是“函数f(x)=log2[(1﹣a)x﹣1]在区间(1,+∞)上单调递增”的( )
A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分也不必要条件
【分析】结合对数复合函数的单调性及充分条件、必要条件的定义,即可得答案.
【解答】解:令u=(1﹣a)x﹣1,y=log2u,
若f(x)=log2[(1﹣a)x﹣1]在(1,+∞)上单调递增,
因为y=log2u是(1,+∞)上的增函数,
则需使u=(1﹣a)x﹣1是(1,+∞)上的增函数且u>0,
则1﹣a>0且1﹣a﹣1≥0,解得a≤0.
因为(﹣∞,0]⫋(﹣∞,1),
故a<1是a≤0的必要不充分条件.
故选:C.
【点评】本题主要考查了复合函数的单调性,考查了充分条件和必要条件的定义,属于基础题.
23.(2023•重庆模拟)函数的单调递减区间为( )
A. B.(﹣∞,﹣1) C. D.(2,+∞)
【分析】求出函数的定义域,根据二次函数、对数函数及复合函数的单调性即可得答案.
【解答】解:由x2﹣x﹣2>0,可得:x<﹣1或x>2,
所以函数的定义域为(﹣∞,﹣1)∪(2,+∞),
令t=x2﹣x﹣2,
由二次函数的性质可知t在(﹣∞,﹣1)上单调递减,在(2,+∞)上单调递增,
又在定义域内为减函数,
由复合函数的性质可知函数y=(x2﹣x﹣2)单调递减区间为(2,+∞).
故选:D.
【点评】本题考查了二次函数、对数函数及复合函数的单调性,属于基础题.
24.(2023•济宁一模)若函数f(x)=loga(ax﹣x3)(a>0且a≠1)在区间(0,1)内单调递增,则a的取值范围是( )
A.[3,+∞) B.(1,3] C. D.
【分析】令μ=g(x)=ax﹣x3,利用导数求出函数g(x)的单调区间,再分a>1和0<a<1两种情况讨论,结合复合函数的单调性即可得解.
【解答】解:令μ=g(x)=ax﹣x3,则g'(x)=a﹣3x2,
当或时,g'(x)<0,当时,g'(x)>0,
所以g(x)在和上递减,在上递增,
当a>1时,y=logaμ为增函数,且函数f(x)在区间(0,1)内单调递增,
所以,解得a≥3,
此时g(x)在(0,1)上递增,则g(x)>g(0)=0恒成立,
当0<a<1时,y=logaμ为减函数,且函数f(x)在区间(0,1)内单调递增,
所以,无解,
综上所述,a的取值范围是[3,+∞).
故选:A.
【点评】本题主要考查复合函数的单调性,对数函数的性质,考查分类讨论思想与运算求解能力,属于中档题.
七.函数的最值及其几何意义(共3小题)
25.(2023•南充模拟)设函数f(x)=|x﹣1|+|x﹣3|,若关于x的方程f(x)=m仅有两个不同的正实数根a,b.
(1)求m的取值范围;
(2)求的最大值.
【分析】(1)作出f(x)的图象,将方程根的问题转化为函数图象交点的问题即可求解;
(2)利用柯西不等式求解即可.
【解答】解:(1)由,
得函数f(x)图像如图所示,
∵f(0)=f(4)=4,
∴2<m<4,即m的取值范围为(2,4).
(2)由f(x)图像可知:其图像关于x=2对称,故a+b=4,
∴,
∴,当且仅当,即时等号成立,
∴的最大值为.
【点评】本题主要考查函数最值的求法,数形结合思想的应用,考查运算求解能力,属于中档题.
26.(2023•温州模拟)已知函数,存在实数x1,x2,…,xn使得f(x1)+f(x2)+…+f(xn﹣1)=f(xn)成立,若正整数n的最大值为6,则a的取值范围为( )
A. B.
C. D.
【分析】设,易知﹣1﹣a<g(x)﹣a<1﹣a,然后分0≤a≤1,a>1,﹣1≤a<0以及a<﹣1讨论即可.
【解答】解:设,
由于单调递减,则g(x)单调递增,
因为e2x+1>1,
所以﹣1<g(x)<1,则﹣1﹣a<g(x)﹣a<1﹣a,
当0≤a≤1时,﹣1﹣a<﹣1,0<1﹣a<1,
则0≤f(x)<a+1,
显然存在任意正整数n,使得f(x1)+f(x2)+…+f(xn﹣1)=f(xn)成立;
当a>1时,﹣1﹣a<1﹣a<0,a﹣1<f(x)<a+1,
要使正整数n的最大值为6,则,解得;
当﹣1≤a<0时,﹣1<﹣1﹣a<0,1﹣a>1,0≤f(x)<1﹣a,
显然存在任意正整数n,使得f(x1)+f(x2)+…+f(xn﹣1)=f(xn)成立;
当a<﹣1时,0<﹣1﹣a<1﹣a,﹣a﹣1<f(x)<﹣1﹣a,
要使正整数n的最大值为6,则,解得.
综上,实数a的取值范围为.
故选:C.
【点评】本题考查绝对值函数的性质,考查分类讨论思想以及运算求解能力,属于中档题.
27.(2023•茂名二模)黎曼函数R(x)是由德国数学家黎曼发现并提出的,它是一个无法用图象表示的特殊函数,此函数在高等数学中有着广泛的应用,R(x)在[0,1]上的定义为:当(p>q,且p,q为互质的正整数)时,;当x=0或x=1或x为(0,1)内的无理数时,R(x)=0,则下列说法错误的是( )
A.R(x)在[0,1]上的最大值为
B.若a,b∈[0,1],则R(a•b)≥R(a)•R(b)
C.存在大于1的实数m,使方程有实数根
D.∀x∈[0,1],R(1﹣x)=R(x)
【分析】根据黎曼函数的定义,逐项分析判断即可.
【解答】解:对于A,由题意,R(x)的值域为,其中p是大于等于2的正整数,选项A正确;
对于B,①若a,b∈(0,1],设(p,q互质,m,n互质),,则R(a•b)≥R(a)•R(b),
②若a,b有一个为0,则R(a•b)≥R(a)•R(b)=0,选项B正确;
对于C,若n为大于1的正数,则,而R(x)的最大值为,
所以该方程不可能有实根,选项C错误;
对于D,x=0,1或(0,1)内的无理数,则R(x)=0,R(1﹣x)=0,R(x)=R(1﹣x),
若x为(0,1)内的有理数,设(p,q为正整数,为最简真分数),则,选项D正确.
故选:C.
【点评】本题考查考查新定义,考查分析问题解决问题的能力,属于中档题.
八.奇函数、偶函数(共2小题)
28.(2023•昌江县二模)已知f(x)是R上的奇函数,且f(x+2)=﹣f(x),当x∈(0,2)时,f(x)=x2+2x,则f(15)=( )
A.3 B.﹣3 C.255 D.﹣255
【分析】由已知结合函数的奇偶性及周期进行转化,代入已知函数解析式可求.
【解答】解:因为f(x)是R上的奇函数,且f(x+2)=﹣f(x),
所以f(x+4)=f(x),
当x∈(0,2)时,f(x)=x2+2x,
则f(15)=f(3)=﹣f(1)=﹣3.
故选:B.
【点评】本题主要考查了函数的奇偶性及周期性在函数值求解中的应用,属于基础题.
29.(2023•重庆一模)设函数f(x)定义域为R,且f(x)﹣1是奇函数,当0≤x≤2时,f(x)=+1;当x>2时,f(x)=2|x﹣4|+1.当k变化时,方程f(x)﹣kx﹣1=0的所有根从小到大记为x1,x2,…,xn,则f(x1)+f(x2)+…+f(xn)取值的集合为( )
A.{1,3} B.{1,3,5} C.{1,3,5,7} D.{1,3,5,7,9}
【分析】先根据题意可作出f(x)在[0,+∞)上的草图,再将方程f(x)﹣kx﹣1=0的根转化成数y=f(x)与直线y=kx+1交点的横坐标,接着数形结合,分类讨论即可求出f(x1)+f(x2)+…+f(xn)的值,从而得解.
【解答】解:∵f(x)﹣1是奇函数,∴y=f(x)关于(0,1)对称,
∵当0≤x≤2时,y=f(x)=+1,∴(x﹣2)2+(y﹣1)2=4,(y≥1),
又当x>2时,f(x)=2|x﹣4|+1,
∴可作出f(x)在[0,+∞)上的草图如下;
又方程f(x)﹣kx﹣1=0的根即为函数y=f(x)与直线y=kx+1交点的横坐标,
数形结合可知:
①当直线y=kx+1为图中l1时,函数与直线只有1个交点,x=0,f(0)=1,
②当直线y=kx+1为图中l2时,函数与直线有3个交点,由图象对称性可知:
f(x1)+f(x2)+f(x3)=1+2×1=3,
③当直线y=kx+1为图中l3时,函数与直线有5个交点,由图象对称性可知:
f(x1)+f(x2)+f(x3)+f(x4)+f(x5)=1+2×1+2×1=5,
④当直线y=kx+1为图中l4时,函数与直线有7个交点,由图象对称性可知:
f(x1)+f(x2)+f(x3)+f(x4)+f(x5)+f(x6)+f(x7)=1+2×1+2×1+2×1=7,
综合可得所求取值的集合为{1,3,5,7}.
故选:C.
【点评】本题考查函数的奇偶性,数形结合思想,方程的根与图象交点的横坐标的转化,分类讨论思想,属中档题.
九.函数奇偶性的性质与判断(共8小题)
30.(2023•全国二模)已知函数f(x)=ax5+bsinx+c,若f(﹣1)+f(1)=2,则c=( )
A.﹣1 B.0 C.1 D.
【分析】代入计算并运用函数奇偶性求解即可.
【解答】解:因为f(﹣1)+f(1)=2,
所以﹣a﹣bsin1+c+a+bsin1+c=2,
所以c=1.
故选:C.
【点评】本题主要考查了函数奇偶性在函数求值中的应用,属于基础题.
31.(2023•重庆模拟)已知函数为奇函数,则sinα= 0 .
【分析】根据函数奇偶性的定义化简可得答案.
【解答】解:由函数为奇函数可得x﹣sinα≠0,f(﹣x)=﹣f(x),
∴,
化简得﹣sinα=sinα,
∴sinα=0,
此时符合题意,
故答案为:0.
【点评】本题主要考查了函数奇偶性的应用,属于基础题.
32.(2023•淇滨区校级模拟)若函数为奇函数,则实数a= ﹣ .
【分析】根据题意,设,由f(x)的奇偶性可得g(x)为偶函数,由此可得,变形可得恒成立,据此分析可得答案.
【解答】解:根据题意,设,则f(x)=xg(x),
函数f(x)为奇函数,即(﹣x)g(﹣x)=﹣xg(x),则有g(x)=g(﹣x),
即,变形可得,
则有恒成立,化简可得x(1+2a)=0恒成立,
则.
故答案为:﹣.
【点评】本题考查函数奇偶性的性质以及应用,涉及对数的运算,属于基础题.
33.(2022•全国)设f(x)是定义域为R的奇函数,g(x)是定义域为R的偶函数.若f(x)+g(x)=2x,则g(2)= .
【分析】由函数的奇偶性的定义和指数的运算性质,解方程可得所求值.
【解答】解:由f(x)是定义域为R的奇函数,可得f(﹣2)=﹣f(2);
由g(x)是定义域为R的偶函数,可得g(﹣2)=g(2).
若f(x)+g(x)=2x,则f(2)+g(2)=4,①
又f(﹣2)+g(﹣2)=﹣f(2)+g(2)=.②
①+②可得2g(2)=,
即有g(2)=.
故答案为:.
【点评】本题考查函数的奇偶性的定义和运用,体现了方程思想和数学运算等核心素养,属于基础题.
34.(2023•全国三模)若对于定义在R上的函数y=f(x),当且仅当存在有限个非零自变量值x0,使得f(﹣x0)=﹣f(x0),则称y=f(x)为类奇函数,若函数y=x4+(a2﹣1)x2+asinx为类奇函数,则实数a的取值范围为 (﹣1,1) .
【分析】根据题意可得x2+a2﹣1=0存在有限个非零实数解,由此可建立关于a的不等式,解出即可.
【解答】解:依题意,令x4+(a2﹣1)x2+asinx+(﹣x)4+(a2﹣1)(﹣x)2+asin(﹣x)=0,
即2x4+2(a2﹣1)x2=0,即x2[x2+(a2﹣1)]=0,
则x2+a2﹣1=0存在有限个非零实数解,
则1﹣a2>0,解得﹣1<a<1.
故答案为:(﹣1,1).
【点评】本题考查函数奇偶性的应用,理解类奇函数的定义,方程有解的含义是解题的关键,考查逻辑推理能力和运算能力,属于中档题.
35.(2023•上虞区二模)已知函数y=f(2x+1)为偶函数,且f(x)+f(﹣x)=2,则f(2022)+f(2024)= 2 .
【分析】根据函数奇偶性和对称性,判断函数是周期为4的周期函数,利用函数的周期性进行转化求解即可.
【解答】解:∵y=f(2x+1)为偶函数,
∴f(﹣2x+1)=f(2x+1),即f(x)关于x=1对称,
则f(﹣x)=f(2+x),
由f(x)+f(﹣x)=2,得函数关于(0,1)对称,
令x=0,得2f(0)=2,得f(0)=1,
则f(x)+f(2+x)=2,
即f(x+2)+f(x+4)=2,
即f(x+2)+f(x+4)=f(x)+f(2+x),
得f(x+4)=f(x),即f(x)是周期为4的周期函数,
令x=0,由f(﹣x)=f(2+x)得,f(0)=f(2),即f(2)=1,
∴f(2022)+f(2024)=f(505×4+2)+f(506×4)=f(2)+f(0)=1+1=2,
故答案为:2.
【点评】本题主要考查函数值的计算,利用函数奇偶性和对称性,求出函数的周期性是解决本题的关键,是中档题.
36.(2022•乙卷)若f(x)=ln|a+|+b是奇函数,则a= ﹣ ,b= ln2 .
【分析】显然a≠0,根据函数解析式有意义可得,x≠1且x,所以1+=﹣1,进而求出a的值,代入函数解析式,再利用奇函数的性质f(0)=0即可求出b的值.
【解答】解:f(x)=ln|a+|+b,
若a=0,则函数f(x)的定义域为{x|x≠1},不关于原点对称,不具有奇偶性,
∴a≠0,
由函数解析式有意义可得,x≠1且a+,
∴x≠1且x,
∵函数f(x)为奇函数,∴定义域必须关于原点对称,
∴1+=﹣1,解得a=﹣,
∴f(x)=ln||+b,定义域为{x|x≠1且x≠﹣1},
由f(0)=0得,ln+b=0,
∴b=ln2,
故答案为:﹣;ln2.
【点评】本题主要考查了奇函数的定义和性质,属于中档题.
37.(2023•江西模拟)已知函数g(x),h(x)分别是定义在R上的偶函数和奇函数,且,若函数f(x)=2023﹣|x﹣2023|﹣λg(x﹣2023)﹣2λ2有唯一零点,则实数λ的值为( )
A.﹣1或 B.﹣1或 C.﹣1 D.
【分析】根据g(x)是R上的偶函数,h(x)为R上的奇函数可得出,从而得出,这样即可得出g(x﹣2023)关于x=2023对称,进而得出f(x)关于x=2023对称,然后根据f(x)有唯一零点得f(2023)=0,从而得出关于λ的方程,解出λ即可.
【解答】解:因为g(x)+h(x)=①,
又函数g(x),h(x)分别是定义在R上的偶函数和奇函数,
则g(﹣x)+h(﹣x)=即g(x)﹣h(x)=②,
①+②可得,,
由于y=|x﹣2023|关于直线x=2023对称,
则y=2023﹣|x﹣2023|关于直线x=2023对称,
因为g(x)为偶函数,则y=g(x)关于y轴对称,
所以g(x﹣2023)关于x=2023对称,
∴f(x)关于x=2023对称,
由于函数f(x)=2023﹣|x﹣2023|﹣λg(x﹣2023)﹣2λ2有唯一零点,
则必有f(2023)=0,且g(0)=1,
即f(2023)=20230﹣λg(0)﹣2λ2=1﹣λ﹣2λ2=0,
解得λ=﹣1或.
故选:A.
【点评】本题考查了奇函数和偶函数的定义,偶函数图象的对称性,函数零点的定义,考查了计算能力,属于中档题.
一十.奇偶函数图象的对称性(共2小题)
38.(2023•晋中模拟)已知函数,则f(x)的图象( )
A.关于直线x=2对称 B.关于点(2,0)对称
C.关于直线x=0对称 D.关于原点对称
【分析】根据函数解析式可得f(x)+f(4﹣x)=0,由此得解.
【解答】解:f(x)=2x﹣24﹣x,
则f(4﹣x)=24﹣x﹣24﹣(4﹣x)=24﹣x﹣2x,
所以f(x)+f(4﹣x)=0,
则函数f(x)的图象关于点(2,0)对称,
故选:B.
【点评】本题考查函数对称性的运用,考查运算求解能力,属于基础题.
39.(2023•安阳三模)已知函数的图象关于坐标原点对称,则a+b= .
【分析】由f(x)的图象关于坐标原点对称得f(x)是一个奇函数,根据定义域关于原点对称及奇函数的性质求得结果.
【解答】解:依题意函数f(x)是一个奇函数,
又2x﹣a≠0,所以x≠log2a,
所以f(x)定义域为{x|x≠log2a},
因为f(x)的图象关于坐标原点对称,所以log2a=0,
解得a=1,
又f(﹣x)=﹣f(x),所以,
所以,即,
所以,所以.
故答案为:.
【点评】本题主要考查了奇函数的性质,属于基础题.
一十一.奇偶性与单调性的综合(共3小题)
40.(2023•林芝市二模)已知定义在R上的函数f(x)在(﹣∞,2]上单调递减,且f(x+2)为偶函数,则不等式f(x﹣1)>f(2x)的解集为( )
A. B.
C. D.
【分析】由f(x+2)为偶函数求得函数对称轴,再结合函数的单调性进行求解即可.
【解答】解:∵函数f(x+2)为偶函数,
∴f(﹣x+2)=f(x+2),即f(2﹣x)=f(2+x),
∴函数f(x)的图象关于直线x=2对称,
又∵函数f(x)定义域为R,在区间(﹣∞,2]上单调递减,
∴函数f(x)在区间(2,+∞)上单调递增,
∴由f(x﹣1)>f(2x)得,|(x﹣1)﹣2|>|2x﹣2|,解得.
故选:D.
【点评】本题主要考查了函数的奇偶性在不等式求解中的应用,属于基础题.
41.(2023•河南三模)已知函数,若f(2x﹣1)+f(2﹣x)>0,则x的取值范围是 (﹣1,+∞) .
【分析】利用定义可判断函数的奇偶性,根据单调性求解双“f”问题.
【解答】解:因为函数,
f(﹣x)+f(x)=+=ln1=0,
所以f(x)是奇函数且在R上单调递增.
∵f(2x﹣1)+f(2﹣x)>0,∴f(2x﹣1)>f(x﹣2),
则2x﹣1>x﹣2,∴x>﹣1.
故答案为:(﹣1,+∞).
【点评】本题考查函数的性质,属于基础题.
42.(2023•九江三模)已知定义在R上的函数f(x)在[0,1]上单调递增,f(x+1)是奇函数,f(x﹣1)的图像关于直线x=1对称,则f(x)( )
A.在[2020,2022]上单调递减
B.在[2021,2023]上单调递增
C.在[2022,2024]上单调递减
D.在[2023,2025]上单调递增
【分析】根据f(x+1)是奇函数得出f(x+1)+f(﹣x+1)=0,从而得出f(x)关于(1,0)对称,然后得出f(x)在[0,2]上单调递增;由f(x+1)=﹣f(﹣x+1)得f(2﹣x)=﹣f(x),而根据f(x﹣1)关于x=1对称得出f(x)为偶函数,从而得出f(x﹣2)=﹣f(x),进而得出f(x+4)=f(x),从而得出f(x)的周期为4,然后即可判断每个选项的正误.
【解答】解:∵f(x+1)是奇函数,∴f(x+1)=﹣f(﹣x+1),即f(x)的图像关于点(1,0)对称,
又∵f(x)在[0,1]上单调递增,∴f(x)在[1,2]上单调递增,即f(x)在[0,2]上单调递增,
由f(x+1)=﹣f(﹣x+1)可得f(2﹣x)=﹣f(x),由f(x﹣1)图像关于直线x=1对称可知f(x)为偶函数,
∴f(2﹣x)=f(x﹣2)=﹣f(x),∴f(x+4)=f(x),
∴f(x)是周期函数,最小正周期为4,且f(x)在[﹣2,0]上单调递减,
∴f(x)在[2022,2024]上单调递减.
故选:C.
【点评】本题考查了奇函数和偶函数的定义,偶函数图象的对称性,偶函数在对称区间上的单调性特点,周期函数的定义,考查了计算能力,属于中档题.
一十二.抽象函数及其应用(共7小题)
43.(2023•青羊区校级模拟)已知定义在R上的函数f(x)满足f(x+3)=﹣f(x),g(x)=f(x)﹣2为奇函数,则f(198)= 2 .
【分析】根据奇函数性质可求得f(0),由已知抽象函数关系式可知f(x)周期为6,由周期性可推导求得结果.
【解答】解:∵g(x)为定义域为R的奇函数,∴g(0)=f(0)﹣2=0,解得:f(0)=2,
由f(x+3)=﹣f(x)得:f(x+6)=﹣f(x+3)=f(x),
∴f(x)是周期为6的周期函数,∴f(198)=f(33×6)=f(0)=2.
故答案为:2.
【点评】本题主要考查抽象函数及其应用,函数奇偶性与周期性的综合,考查运算求解能力,属于基础题.
44.(2023•江西模拟)已知函数f(x)是偶函数,对任意x∈R均有f(x)+f(8﹣x)=6,f(8)=4,f(﹣2)+f(2)=5,则下列正确结论的序号为( )
①f(0)=2;②f(x﹣4)是奇函数;③直线x=8是f(x)图像的一条对称轴;④记,则.
A.①②④ B.①③④ C.①④ D.②③
【分析】令x=0,可判断①;令x=4,得f(﹣4)=3≠0,可判断②;由条件可得f(x)=f(x+16),故16是f(x)的一个周期,进而得f(16﹣x)=f(﹣x)=f(x),可判断③;由条件结合③求得f(2),f(4),f(6),f(8),f(10),f(12),f(14),f(16),结合函数的周期性求解可判断④.
【解答】解:令x=0,知f(0)+f(8)=6,故f(0)=2,故①正确;
令x=4,知f(4)+f(4)=6,故f(4)=3,又f(x)为偶函数,
故f(﹣4)=3≠0,则f(x﹣4)不是奇函数,故②错误;
因为f(﹣x)=f(x),f(x)+f(8﹣x)=6,则f(﹣x)+f(8+x)=6,即f(x)+f(x+8)=6,
于是有f(x+8)+f(x+16)=6,则f(x)=f(x+16),故16是f(x)的一个周期,
则f(16﹣x)=f(﹣x)=f(x),故f(x)的图像关于x=8对称,故③正确;
因为f(2)=f(﹣2),f(﹣2)+f(2)=5,所以,
由③可知f(2)=f(14),故,
因为f(2)+f(6)=6,故,
又f(16)=f(0)=2,f(4)=f(12)=3,
故f(2)+f(4)+f(6)+f(8)+f(10)+f(12)+f(14)+f(16)=24,,故④正确.
综上,①③④正确.
故选:B.
【点评】本题主要考查了抽象函数的应用,考查了函数的奇偶性,对称性和周期性,属于中档题.
45.(2023•长沙模拟)设函数f(x),f'(x)的定义域均为R,且函数f(2x﹣1),f'(x﹣2)均为偶函数.若当x∈[1,2]时,f'(x)=ax3+1,则f'(2022)的值为 ﹣7 .
【分析】对函数求导,根据函数的奇偶性,对称性,周期性分析即可求解.
【解答】解:因为函数f(2x﹣1)为偶函数,
则f(﹣2x﹣1)=f(2x﹣1),
又﹣f'(﹣2x﹣1)=f'(2x﹣1),
即f'(x﹣1)=﹣f'(﹣x﹣1),
所以函数y=f'(x)的图像关于(﹣1,0)对称.
因为函数f'(x﹣2)为偶函数,
所以f'(x﹣2)=f′(﹣x﹣2),
所以函数y=f'(x)的图像关于x=﹣2对称,
由函数y=f'(x)的图像关于(﹣1,0)对称,且关于直线x=﹣2对称.
所以函数y=f'(x)的周期为T=4×[﹣1﹣(﹣2)]=4,.
由f'(x﹣1)=﹣f'(﹣x﹣1)⇒f'(﹣1)=﹣f'(﹣1)⇒f'(﹣1)=0,
f'(x﹣1)=﹣f'(﹣x﹣1)⇒f'(1)=﹣f'(﹣3)⇒f'(1)+f'(﹣3)=0,f'(x﹣2)=f'(﹣x﹣2)⇒f'(﹣1)=f'(﹣3)=0,
所以f'(1)=0,即a+1=0,即a=﹣1,
所以当x∈[1,2]时,f'(x)=﹣x3+1,
于是f'(2022)=f'(505×4+2)=f'(2)=﹣23+1=﹣8+1=﹣7.
故答案为:﹣7.
【点评】本题主要考查了函数的奇偶性,对称性在函数求值中的应用,还考查了导数的求解,属于中档题.
46.(2022•乙卷)已知函数f(x),g(x)的定义域均为R,且f(x)+g(2﹣x)=5,g(x)﹣f(x﹣4)=7.若y=g(x)的图像关于直线x=2对称,g(2)=4,则f(k)=( )
A.﹣21 B.﹣22 C.﹣23 D.﹣24
【分析】由y=g(x)的对称性可得f(x)为偶函数,进而得到f(x)关于点(﹣1,﹣1)中心对称,所以f(1)=f(﹣1)=﹣1,再结合f(x)的周期为4,即可求出结果.
【解答】解:∵y=g(x)的图像关于直线x=2对称,则g(2﹣x)=g(2+x),
∵f(x)+g(2﹣x)=5,∴f(﹣x)+g(2+x)=5,∴f(﹣x)=f(x),故f(x)为偶函数,
∵g(2)=4,f(0)+g(2)=5,得f(0)=1.由g(x)﹣f(x﹣4)=7,得g(2﹣x)=f(﹣x﹣2)+7,代入f(x)+g(2﹣x)=5,得f(x)+f(﹣x﹣2)=﹣2,故f(x)关于点(﹣1,﹣1)中心对称,
∴f(1)=f(﹣1)=﹣1,由f(x)+f(﹣x﹣2)=﹣2,f(﹣x)=f(x),得f(x)+f(x+2)=﹣2,
∴f(x+2)+f(x+4)=﹣2,故f(x+4)=f(x),f(x)周期为4,
由f(0)+f(2)=﹣2,得f(2)=﹣3,又f(3)=f(﹣1)=f(1)=﹣1,
所以f(k)=6f(1)+6f(2)+5f(3)+5f(4)=11×(﹣1)+5×1+6×(﹣3)=﹣24,
故选:D.
【点评】本题主要考查了函数的奇偶性、对称性和周期性,属于中档题.
47.(2023•青秀区校级一模)已知f'(x),g'(x)分别为定义在R上的f(x),g(x)的导函数,且f(x)﹣g'(x)=2,f(x)+g'(2﹣x)=2,若g(x)是偶函数,则下列结论一定正确的是( )
A.函数f(x)的图象关于点(1,1)对称
B.函数f'(x)的图象关于直线x=2对称
C.3是g'(x)的一个周期
D.f(2024)=1
【分析】根据函数f(x)与f′(x),g′(x)之间的关系分别进行转化判断即可.
【解答】解:∵g(x)是偶函数,∴g(﹣x)=g(x),则﹣g′(﹣x)=g′(x),即g′(﹣x)=﹣g′(x),则g′(x)是奇函数,图象关于原点对称,
由f(x)﹣g'(x)=2得f(x)=g'(x)+2,则f(x)的图象关于(0,2)对称,
由f(x)﹣g'(x)=2,f(x)+g'(2﹣x)=2,得﹣g'(x)=g'(2﹣x),则g′(x)也关于点(1,0)对称,则f(x)的图象关于(1,2)对称,故A错误,
由f(x)=g'(x)+2,得f′(x)=g″(x),
∵g′(x)是奇函数,∴g′(﹣x)=﹣g′(x),则﹣g″(﹣x)=﹣g″(x),即g″(﹣x)=g″(x),则g″(x)是偶函数,则图象关于x=0对称,则f′(x)的图象关于x=0对称,
由f(x)﹣g'(x)=2,f(x)+g'(2﹣x)=2得f(x)﹣g'(x)=f(x)+g'(2﹣x),
即﹣g'(x)=g'(2﹣x),
∵g′(x)是奇函数,∴﹣g'(x)=g'(2﹣x)=﹣g'(x﹣2),即g'(x﹣2)=g'(x),即g'(x+2)=g'(x),则g'(x)的周期是2,故C错误,
∵f(x)﹣g'(x)=2,∴f(x)的周期和g′(x)的周期相同,f(x)的周期和f′(x)的周期相同,
∴f′(x)的周期是2,
∵f′(x)的图象关于x=0对称,∴f′(x)的图象也关于x=2对称,故B正确,
由f(x)﹣g'(x)=2得f(x)=g'(x)+2,则f(2024)=g'(2024)+2=g′(0)+2=2,故D错误.
故选:B.
【点评】本题考查抽象函数的应用,利用函数奇偶性和导数之间的关系进行转化是解决本题的关键,是中档题.
48.(2023•浙江模拟)对任意x∈R,恒有f(1﹣x)=f(x+1)=f(x﹣1),对任意,现已知函数y=f(x)的图像与y=kx有4个不同的公共点,则正实数k的值为 .
【分析】由,得f(x)=1﹣x2(0≤x≤1),由已知条件可得函数f(x)的图像的对称性和周期性,可作出函数f(x)的图像,由题意y=kx(k>0)的图像函数y=f(x)在[3,5]上的图像相切,联立方程组利用判别式求解.
【解答】解:,sinθ∈[0,1],f(sinθ)=cos2θ=1﹣sin2θ,
令x=sinθ,则有f(x)=1﹣x2(0≤x≤1),
任意x∈R,恒有f(1﹣x)=f(x+1)=f(x﹣1),
则函数f(x)的图像关于x=1对称,函数f(x)是以2为周期的周期函数,
在同一直角坐标系下作出函数y=f(x)与y=kx(k>0)的图像,如图所示,
函数y=f(x)的图像与y=kx有4个不同的公共点,
由图像可知,y=kx(k>0)的图像函数y=f(x)在[3,5]上的图像相切,
由,得x2+(k﹣8)x+15=0,
则,解得.
故答案为:.
【点评】本题考查分段函数的应用,数形结合思想,属中档题.
49.(2022•新高考Ⅱ)已知函数f(x)的定义域为R,且f(x+y)+f(x﹣y)=f(x)f(y),f(1)=1,则f(k)=( )
A.﹣3 B.﹣2 C.0 D.1
【分析】先根据题意求得函数f(x)的周期为6,再计算一个周期内的每个函数值,由此可得解.
【解答】解:令y=1,则f(x+1)+f(x﹣1)=f(x),即f(x+1)=f(x)﹣f(x﹣1),
∴f(x+2)=f(x+1)﹣f(x),f(x+3)=f(x+2)﹣f(x+1),
∴f(x+3)=﹣f(x),则f(x+6)=﹣f(x+3)=f(x),
∴f(x)的周期为6,
令x=1,y=0得f(1)+f(1)=f(1)×f(0),解得f(0)=2,
又f(x+1)=f(x)﹣f(x﹣1),
∴f(2)=f(1)﹣f(0)=﹣1,
f(3)=f(2)﹣f(1)=﹣2,
f(4)=f(3)﹣f(2)=﹣1,
f(5)=f(4)﹣f(3)=1,
f(6)=f(5)﹣f(4)=2,
∴,
∴=f(1)+f(2)+f(3)+f(4)=﹣3.
故选:A.
【点评】本题考查抽象函数以及函数周期性的运用,考查运算求解能力,属于中档题.
一十三.函数的周期性(共3小题)
50.(2023•南昌二模)f(x)是以2为周期的函数,若x∈[0,1]时,f(x)=2x,则f(3)= 2 .
【分析】直接根据函数的周期性求解即可.
【解答】解:因为f(x)是以2为周期的函数,若x∈[0,1]时,f(x)=2x,
所以f(3)=f(1)=2.
故答案为:2.
【点评】本题主要考查函数的周期性,属于基础题.
51.(2023•乌鲁木齐模拟)已知定义在R上的奇函数f(x),满足f(x+3)=﹣f(x),且当时,f(x)=x2﹣6x+8,则f(0)+f(1)+f(2)+…+f(100)=( )
A.6 B.3 C.0 D.﹣3
【分析】根据函数f(x)恒有f(x+3)=﹣f(x),得到函数f(x)的周期是6,再由f(x)定义在R上的奇函数,得到f(0)=0,f(3)=0,然后f(0)+f(1)+f(2)+...+f(100)=[f(0)+f(1)+f(2)+...+f(5)]×16+f(0)+f(1)+f(2)+f(3)+f(4)求解.
【解答】解:因为函数f(x)对任意的实数x,恒有f(x+3)=﹣f(x),
所以f(x+6)=﹣f(x+3)=f(x),
所以函数f(x)是以6为周期的周期函数,
又f(x)定义在R上的奇函数,
所以f(0)=0,f(3)=﹣f(0)=0,
又当时,f(x)=x2﹣6x+8,
所以f(1)=3,f(2)=f(﹣1+3)=﹣f(﹣1)=f(1)=3,f(4)=f(1+3)=﹣f(1)=﹣3,f(5)=f(2+3)=﹣f(2)=﹣3,
所以f(0)+f(1)+f(2)+...+f(100)=[f(0)+f(1)+f(2)+...+f(5)]×16+f(0)+f(1)+f(2)+f(3)+f(4)=0×16+3=3.
故选:B.
【点评】本题主要考查函数的周期性,考查转化能力,属于基础题.
52.(2023•上饶二模)关于函数,有如下四个命题:
①函数f(x)的图像关于y轴对称;
②函数f(x)的图像关于直线对称;
③函数f(x)的最小正周期为2π;
④函数f(x)的最小值为2.其中所有真命题的序号是 ①②④ .
【分析】对于①:由奇偶函数的定义,可判断出f(x)为偶函数,图像关于y轴对称;对于②:由f(π﹣x)=f(x)即可判断出函数f(x)的图像关于直线对称;对于③:由f(π+x)=f(x)得出函数f(x)的最小正周期为π;对于④:设,则,由基本不等式即可求出最小值.
【解答】解:对于①:f(x)定义域为R,
因为,所以f(x)是R上的偶函数,
所以f(x)图像关于y轴对称,故①正确;
对于②:对于任意的x∈R,,
所以函数f(x)的图像关于直线对称,故②正确;
对于③:因为,
所以函数f(x)的最小正周期为π,故③错误;
对于④:设,
则,
因为,当且仅当,即t=1时等号成立,
所以函数f(x)的最小值为2,故④正确,
故答案为:①②④.
【点评】本题主要考查了函数奇偶性的判断,考查了函数的对称性和周期性,属于中档题.
一十四.函数恒成立问题(共8小题)
53.(2023•惠州一模)若函数f(x)的定义域为D,如果对D中的任意一个x,都有f(x)>0,﹣x∈D,且f(﹣x)f(x)=1,则称函数f(x)为“类奇函数”.若某函数g(x)是“类奇函数”,则下列命题中,错误的是( )
A.若0在g(x)定义域中,则g(0)=1
B.若g(x)max=g(4)=4,则
C.若g(x)在(0,+∞)上单调递增,则g(x)在(﹣∞,0)上单调递减
D.若g(x)定义域为R,且函数h(x)也是定义域为R的“类奇函数”,则函数G(x)=g(x)h(x)也是“类奇函数”
【分析】对A,根据“类奇函数”的定义,代入x=0求解即可;对B,根据题意可得,再结合函数的单调性判断即可;对C,根据,结合g(x)的单调性判断即可;对D,根据“类奇函数”的定义,推导G(x)G(﹣x)=1判断即可.
【解答】解:对于A,由函数g(x)是“类奇函数”,所以g(x)g(﹣x)=1,且g(x)>0,
所以当x=0时,g(0)g(﹣0)=1,即g(0)=1,故A正确;
对于B,由g(x)g(﹣x)=1,即随g(x)的增大而减小,
若g(x)max=g(4)=4,则成立,故B正确;
对于C,由g(x)在(0,+∞)上单调递增,
所以,在x∈(0,+∞)上单调递减,设t=﹣x∈(﹣∞,0),
∴g(t)在t∈(﹣∞,0)上单调递增,即g(x)在x∈(﹣∞,0)上单调递增,故C错误;
对于D,由g(x)g(﹣x)=1,h(x)h(﹣x)=1,
所以G(x)G(﹣x)=g(x)g(﹣x)h(x)h(﹣x)=1,
所以函数G(x)=g(x)h(x)也是“类奇函数”,故D正确;
故选:C.
【点评】本题主要考查了新定义问题,考查了利用函数的单调性求函数的最值,属于中档题.
54.(2023•遂宁模拟)已知函数f(x)=|x﹣t|+|x+t|,t∈R.
(1)若t=1,求不等式f(x)≤8﹣x2的解集;
(2)已知m+n=4,若对任意x∈R,都存在m>0,n>0使得f(x)=,求实数t的取值范围.
【分析】(1)将t=1代入,再将f(x)写成分段函数,分段求解后取并集即可;
(2)由绝对值三角不等式可得f(x)min=2|t|,由基本不等式可得≥,从而有,求解即可.
【解答】解:(1)当t=1时,f(x)=|x﹣t|+|x+t|=|x﹣1|+|x+1|=,
∵f(x)≤8﹣x2,
当x>1时,即2x≤8﹣x2,∴1<x≤2;
当﹣1≤x≤1时,即2≤8﹣x2,∴﹣1≤x≤1;
当x<﹣1时,即﹣2x≤8﹣x2,∴﹣2≤x<﹣1,
综上可得不等式的解集为[﹣2,2];
(2)∵f(x)=|x﹣t|+|x+t|≥|(x﹣t)﹣(x+t)|=2|t|,当且仅当(x﹣t)(x+t)≤0时取等号,
∴f(x)min=2|t|,
又m>0,n>0且m+n=4,∴=,
当且仅当,即,时等号成立,
所以,
根据题意可得,解得或,
∴t的取值范围是.
【点评】本题考查了绝对值不等式的解法、绝对值三角不等式、基本不等式的应用,属于中档题.
55.(2023•平江县模拟)若对任意x∈(0,2),恒成立,则实数a的取值集合为 {2} .
【分析】构造函数g(x)=alnx+1﹣,0<x<2,令g(x)≤0恒成立,结合g(1)=0,再利用g(x)的单调性验证g(1)是该函数的极大值,也是最大值即可.
【解答】解:由题意设g(x)=alnx+1﹣,0<x<2,
由题意g(x)≤0恒成立,显然g(1)=0,所以g(x)max=g(1)=0,且g′(1)=0,
又,所以g′(1)=a﹣2=0,即a=2,
当a=2时,g′(x)=,当0<x<2时,x2﹣5x+8>0,(x﹣2)3<0,
所以当∈(0,1)时,g′(x)>0,当x∈(1,2)时,g′(x)<0,
所以g(x)≤g(1)=0,符合题意,
故实数a的取值集合为{2}.
故答案为:{2}.
【点评】本题考查利用导数研究函数的单调性和最值,进而解决不等式恒成立问题的解题思路,属于中档题.
56.(2023•雁塔区校级三模)已知函数f(x)=|x﹣a|+2|x+1|.
(1)当a=1时,解关于x的不等式f(x)≤6;
(2)已知g(x)=|x﹣1|+2,若对任意x1∈R,都存在x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
【分析】(1)当a=1时,利用绝对值的意义,将f(x)表示成分段函数形式,然后求不等式即可.
(2)利用对任意x1∈R,都存在x2∈R,使得f(x1)=g(x2)成立,转化为{y|y=f(x)}⊆{y|y=g(x)},然后利用不等式的性质求最值关系即可.
【解答】解:(1)当a=1时,f(x)=|x﹣1|+2|x+1|,则f(x)=,
当x<﹣1时,由﹣3x﹣1≤6,得﹣≤x<﹣1;
当﹣1≤x≤1时,f(x)≤6恒成立:
当x>1时,由3x+1≤6,得1<x≤,
综上,﹣≤x≤,
即f(x)≤6的解集为[﹣,].
(2)∵对任意x1∈R,都存在x2∈R,使得f(x1)=g(x2)成立,
∴{y|y=f(x)}⊆{y|y=g(x)},
又f(x)=|x﹣a|+2|x+1|≥|x﹣a﹣(x+1)|+|x+1|=|a+1|+|x+1|≥|a+1|,当x=﹣1时等号成立,
g(x)=|x﹣1|+2≥2,
∴|a+1|≥2,解得a≥1或a≤﹣3,
..实数a 的取值范围是(﹣∞,﹣3]∪[1,+∞).
【点评】本题主要考查绝对值不等式的应用,根据绝对值的意义,求出f(x)的表达式,利用分类讨论思想进行求解是解决本题的关键,是中档题.
57.(2023•全国三模)已知函数f(x)=|x+4|+|x﹣2a|.
(1)当a=2时,求不等式f(x)≤13的解集;
(2)若f(x)≥a2+5a恒成立,求实数a的取值范围.
【分析】(1)把a=2代入,将函数化为分段函数的形式,然后列出不等式组求解即可得到结果.
(2)利用绝对值三角不等式可得f(x)≥|2a+4|,即可转化为|2a+4|≥a2+5a,解出即可.
【解答】解:(1)当a=2时,f(x)=|x+4|+|x﹣4|,
不等式f(x)≤13,即为|x+4|+|x﹣4|≤13,
则或或,
解得或﹣4<x<4或,
故不等式f(x)≤13的解集为.
(2)f(x)=|x+4|+|x﹣2a|≥|x+4﹣(x﹣2a)|=|2a+4|(当且仅当(x+4)(x﹣2a)≤0时等号成立),
因为f(x)≥a2+5a恒成立,所以|2a+4|≥a2+5a,
所以2a+4≥a2+5a①或2a+4≤﹣(a2+5a)②,
由①解得﹣4≤a≤1,由②解得.
综上所述,,
故实数a的取值范围是.
【点评】本题主要考查绝对值不等式的解法,不等式恒成立求参数范围问题,考查运算求解能力,属于中档题.
58.(2023•青羊区校级模拟)已知函数f(x)=|x﹣1|﹣|x+1|+x.
(1)解不等式;
(2)是否存在正实数k,使得对任意的实数x,都有f(x+k)≥f(x)成立?若存在,求出k的取值范围;若不存在,请说明理由.
【分析】(1)将函数f(x)化为分段函数的形式,再分别讨论解不等式即可;
(2)结合函数f(x)的图象可知k≥4,再进一步证明.
【解答】解:(1),
①当x<﹣1时,,,x<﹣6;
②当﹣1≤x≤1时,,则,,则;
③当x>1时,,,x<2,则1<x<2.
综上所述,不等式的解集为.
(2)函数的图象如下图所示,
假设存在正实数k,使得对任意的实数x,都有f(x+k)≥f(x)成立.
当x=﹣1时,因为f(﹣1+k)≥f(﹣1)=1=f(3)成立,
结合函数f(x)的图象可知,﹣1+k≥3,所以k≥4.
下面进一步验证:若k≥4,则 x∈(﹣∞,﹣1)⋃(﹣1,+∞),f(x+k)≥f(k)成立.
①当x∈(﹣∞,﹣1)时,f(x+k)﹣f(x)=x+k+|x+k﹣1|﹣|x+k+1|﹣(x+2)=k+|x+k﹣1|﹣|x+k+1|﹣2,
因为|x+k﹣1|﹣|x+k+1|≥﹣|(x+k﹣1)﹣(x+k+1)|=﹣2,
所以f(x+k)﹣f(x)≥k﹣2﹣2≥0,所以f(x+k)≥f(x)成立.
②当x∈(﹣1,+∞)时,
f(x+k)﹣f(x)=x+k﹣2﹣(x+|x﹣1|﹣|x+1|)=k﹣2﹣|x﹣1|+|x+1|.
因为|x+1|﹣|x﹣1|≥﹣|(x+1)﹣(x﹣1)|=﹣2,
所以f(x+k)﹣f(x)≥k﹣2﹣2≥0,所以f(x+k)≥f(x)成立.
综上所述,存在正实数k,使得对任意的实数x,都有f(x+k)≥f(x)成立,
此时k的取值范围是[4,+∞).
【点评】本题考查绝对值函数的运用,考查不等式的恒成立问题,考查分类讨论思想以及运算求解能力,属于中档题.
59.(2023•广西模拟)已知函数,
(1)当a=3时,求f(x)的最小值;
(2)若对∀m∈(0,6),∀x∈R,不等式恒成立,求a的取值范围.
【分析】(1)首先化简得f(x)=|x﹣a|+|x﹣2a+1|,利用绝对值不等式即可求出f(x)的最小值;
(2)利用三元基本不等式求出,再根据绝对值不等式得f(x)≥|a﹣1|,则有|a﹣1|>8,解出即可.
【解答】解:(1)化简得f(x)=|x﹣a|+|x﹣2a+1|,
当a=3时,f(x)=|x﹣3|+|x﹣5|≥|(x﹣3)﹣(x﹣5)|=2,
当3≤x≤5时等号成立,所以f(x)的最小值为2;
(2)由基本不等式得,
当且仅当m=12﹣2m,即m=4时,等号成立.
又因为f(x)=|x﹣a|+|x﹣2a+1|≥|(x﹣a)﹣(x﹣2a+1)|=|a﹣1|,
当且仅当(x﹣a)(x﹣2a+1)≤0时,等号成立.
所以|a﹣1|>8,
解得a>9或a<﹣7,
即a的取值范围为{a|a>9或a<﹣7}.
【点评】本题主要考查了绝对值不等式的解法,考查了利用基本不等式求最值,属于中档题.
60.(2023•江西模拟)已知函数.
(1)求函数f(x)在区间[1,2]上的最大值;
(2)若m为整数,且关于x的不等式f(x)≥lnx恒成立,求整数m的最小值.
【分析】(1)讨论m的取值范围,结合二次函数的对称轴与区间的位置关系,即可求得答案;
(2)将不等式f(x)≥lnx恒成立,转化为函数的最值问题,即设,利用导数求其最值,分类讨论,即可求得答案.
【解答】解:(1)若m=0时,f(x)=﹣x﹣1,f(x)在区间[1,2]上单调递减,
所以f(x)max=﹣2,
若m>0,则二次函数图象对称轴,
当,即时,1离对称轴近,2离对称轴远,
所以f(x)max=f(2)=4m﹣3,
当,即时,1离对称轴远,2离对称轴近,,
若m<0,对称轴在区间[1,2]上单调递减,,
综上,.
(2)因为f(x)≥lnx恒成立,
即恒成立,
令,
所以,
当m≤0时,因为x>0,所以G′(x)>0,
所以G(x)在(0,+∞)上是单调递增函数,
又因为,所以关于x的不等式G(x)≤0不能恒成立,
当m>0时,,
令G'(x)=0得,所以当时,G′(x)>0;当时,G′(x)<0,
因此函数G(x)在上是增函数,在上是减函数,
故函数G(x)的最大值为.
令,因为,
又因为h(m)在m∈(0,+∞)上是减函数,所以当m≥2时,h(m)<0,
即关于x的不等式G(x)≤0恒成立,
所以整数m的最小值为2.
【点评】本题主要考查函数恒成立问题,函数最值的求法,考查运算求解能力,属于中档题.
相关试卷
这是一份综合训练01集合与常用逻辑用语(18种题型60题专练)-【一轮复习讲义】2024年高考数学复习全程规划(新高考地区专用)(原卷版),共8页。
这是一份综合训练06函数的应用(8种题型60题专练)-【一轮复习讲义】2024年高考数学复习全程规划(新高考地区专用)(原卷版),共17页。试卷主要包含了给出下列命题,=|x﹣m|等内容,欢迎下载使用。
这是一份综合训练06函数的应用(8种题型60题专练)-【一轮复习讲义】2024年高考数学复习全程规划(新高考地区专用)(解析版),共61页。试卷主要包含了给出下列命题,=|x﹣m|等内容,欢迎下载使用。









