初一数学秋季讲义 第14讲 图形中的观察、归纳与猜想

                  壮壮饿了…

从一个简单的、基本的图形开始，按照一定的规律，变化成复杂、有趣而美丽的图形，并探寻图形的边长、周长、面积的变化规律，这类图形变化的问题是近年中考、竞赛的一个热点问题．

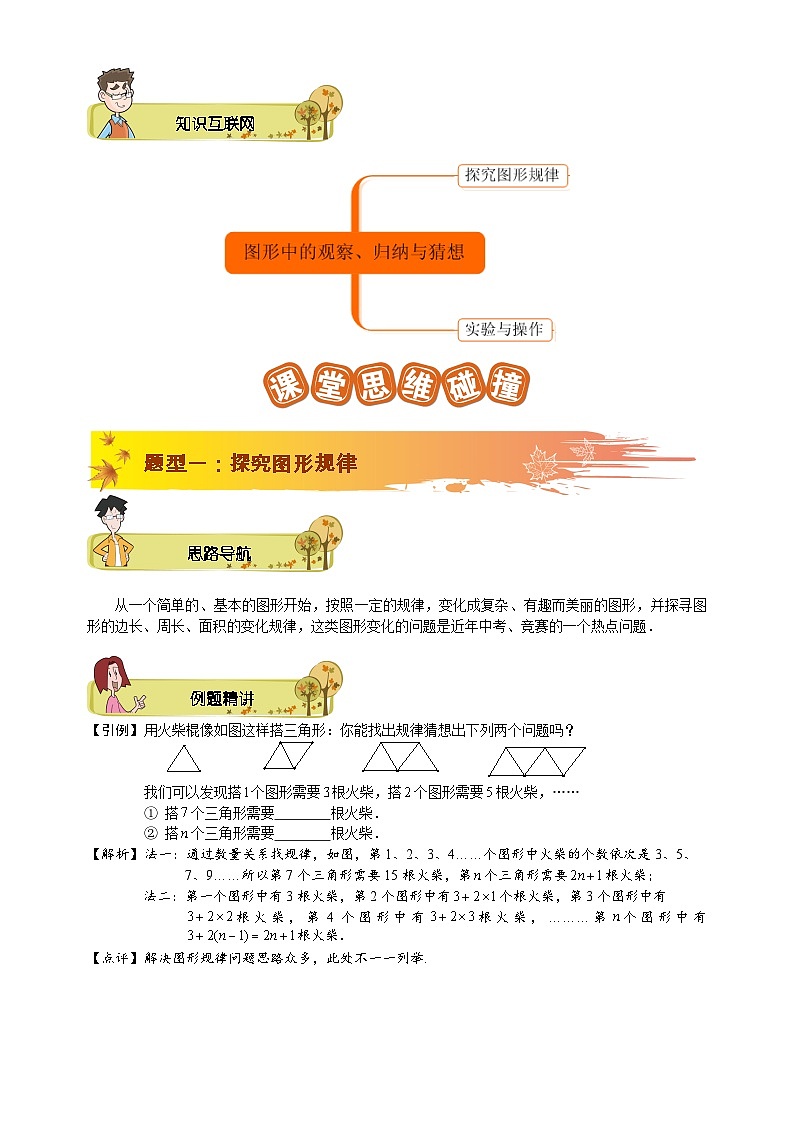
【引例】       用火柴棍像如图这样搭三角形：你能找出规律猜想出下列两个问题吗？

我们可以发现搭个图形需要根火柴，搭个图形需要根火柴，……

① 搭个三角形需要        根火柴．

② 搭个三角形需要        根火柴．

【解析】       法一：通过数量关系找规律，如图，第1、2、3、4……个图形中火柴的个数依次是3、5、

7、9……所以第7个三角形需要15根火柴，第个三角形需要根火柴；

法二：第一个图形中有3根火柴，第2个图形中有个根火柴，第3个图形中有

根火柴，第4个图形中有根火柴，………第个图形中有根火柴．

【点评】       解决图形规律问题思路众多，此处不一一列举.

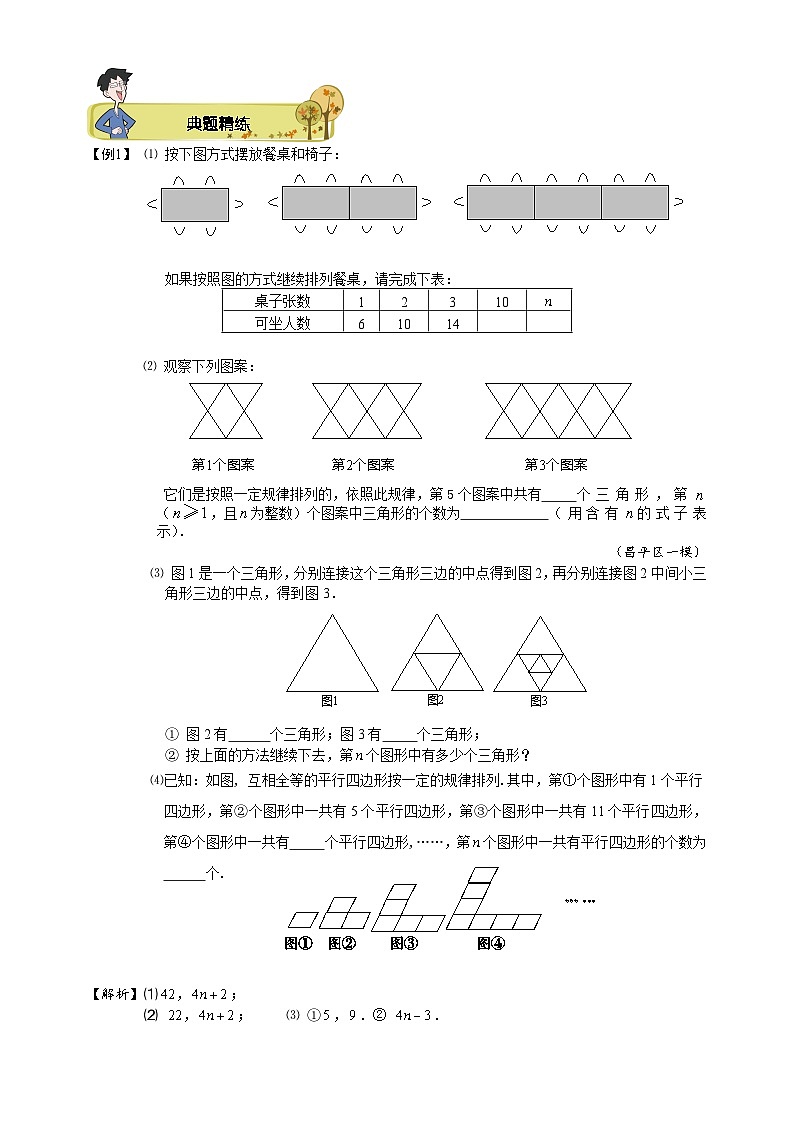
【例1】         ⑴ 按下图方式摆放餐桌和椅子：

如果按照图的方式继续排列餐桌，请完成下表：

⑵ 观察下列图案：

它们是按照一定规律排列的，依照此规律，第5个图案中共有     个三角形，第 （，且为整数）个图案中三角形的个数为                          （用含有的式子表示）．

（昌平区一模）

⑶ 图1是一个三角形，分别连接这个三角形三边的中点得到图2，再分别连接图2中间小三

角形三边的中点，得到图3．

① 图2有      个三角形；图3有     个三角形；

② 按上面的方法继续下去，第个图形中有多少个三角形？

⑷已知：如图, 互相全等的平行四边形按一定的规律排列.其中，第①个图形中有1个平行

四边形，第②个图形中一共有5个平行四边形，第③个图形中一共有11个平行四边形，第④个图形中一共有     个平行四边形,……，第个图形中一共有平行四边形的个数为

      个.

【解析】       ⑴，；

⑵ ，；  　 ⑶ ①，．② ．

⑷ 19，

【备选】如图是由大小相同的小立方体木块叠加而成的几何体，图1中有个立方体，图2中有个

立方体，图3中有个立方体，……，按这样的规律叠放下去，第8个图中小立方体个数

是          ．

【解析】       ．

【例2】         ⑴观察下列图形（每幅图中最小的三角形都是一样的），请写出第个图中最小的三角形的个

数有           个．                                              

⑵ 如图摆放在地上的正方体的大小均相等，现在把露在外面的表面涂成红色，

从上向下数，每层正方体被涂成红色的面数分别为：

第一层：侧面个数上面个数；

第二层：侧面个数上面个数；

第三层：侧面个数上面个数；

第四层：侧面个数上面个数；

…………

根据上述的计算方法，总结规律，并完成下列问题：

① 求第层有多少个面被涂成了红色？

② 求第层有多少个面被涂成了红色？（用含的式子表示）

③ 若第层有个面被涂成红色，请你判断这是第几层？并说明理由．

【解析】       ⑴；

⑵ ① 第层：侧面个数上面个数，

故第层有个面被涂成了红色．

②第层：被涂成了红色的面的个数为：

．

③依题意可得：，∴

∴，故这是第层．

【例3】         如图，将一张正方形纸片，剪成四个大小形状一样的小正方形，然后将其中的一个小正方形再按同样的方法剪成四个小正方形，再将其中的一个小正方形剪成四个小正方形，如此循环进行下去：

⑴ 填表：

⑵ 如果剪了次，共剪出多少个小正方形？

⑶ 如果剪次，共剪出多少个小正方形？

⑷ 观察图形，你还能得出什么规律？

【解析】       ⑴ 如表．

⑵ 如果剪了次，共剪出个小正方形；

⑶ 如果剪次，共剪出个小正方形；

⑷ 观察图形，还能得出的规律是：剪次，最小正方形的边长为原来的．

【例4】         ⑴假设有足够多的黑白围棋子，按照一定的规律排成一行，如图：

……

那么请问第个棋子是黑的还是白的？答：              ．

⑵在数学活动课上，小红同学准备用两种不同颜色的布拼接一个正方形杯垫，杯垫的图案设

计如图所示，最后应选择下图中的哪一个才能使其与上图拼接后符合图案的设计模式？（    ）． 

⑶ 在数学活动课上，张老师设计了一个游戏，让电动娃娃在边长为

1的正方形的四个顶点上依次跳动．规定：从顶点A出发，每跳动一

步的长均为1．第一次顺时针方向跳1步到达顶点D，第二次逆时针

方向跳2步到达顶点B，第三次顺时针方向跳3步到达顶点C，

第四次逆时针方向跳4步到达顶点C，… ，以此类推，跳动第10次

到达的顶点是        ，跳动第2012次到达的顶点是         ．

⑷ 如图所示，圆圈内分别标有1，2，…，12，这12个数字，电

子跳蚤每跳一步，可以从一个圆圈逆时针跳到相邻的圆圈，若

电子跳蚤所在圆圈的数字为，则电子跳蚤连续跳（）

步作为一次跳跃，例如：电子跳蚤从标有数字1的圆圈需跳

步到标有数字2的圆圈内，完成一次跳跃，第二

次则要连续跳步到达标有数字6的圆圈，…依此

规律，若电子跳蚤从①开始，那么第3次能跳到的圆圈内所标

的数字为      ；第2012次电子跳蚤能跳到的圆圈内所标的

数字为       ．

【解析】       ⑴黑的；⑵ A；⑶ B；C；⑷10；6．

有效的数学学习不是单纯地依赖模仿与记忆，动手实践、自主探索是学习数学的重要方法．解实验操作题的关键是：在实验与操作获得直观形象经验的基础上，能发现规律，将其转化为一个数学问题．

图形的翻折与剪拼是实验与操作题中经常遇到的问题，学生应熟练掌握.

【例5】         选择填空．

⑴ 如图，等边的边长为，、分别是、上的点， 将沿直线折叠，点落在点 处，且点在外部，则阴影部分图形的周长为        ．

⑵ 甲乙两人各用一张正方形的纸片折出一个的角（如图），

两人做法如下：

甲：将纸片沿对角线折叠，使点落在点上，则；

乙：将纸片沿、折叠，分别使、落在对角线上的一点，则

对于两人的做法，下列判断正确的是（    ）．

A．甲乙都对      B．甲对乙错       C．甲错乙对        D．甲乙都错

⑶ 把三张大小相同的正方形卡片A，B，C叠放在一个底面为正

方形的盒底上，底面未被卡片覆盖的部分用阴影表示．若按图

1摆放时，阴影部分的面积为S1；若按图2摆放时，阴影部分

的面积为S2，则S1       S2（填“＞”、“＜”或“=”）．

【解析】       ⑴ ；⑵ A；⑶ S1 = S2．

【例6】         ⑴ 如图所示，把一个正方形纸片三次对折后沿虚线剪下，则展平后所得的图形是（    ）．

A．     B．     C．      D．

（西城区期末）

⑵ 如下图①，小强拿一张正方形的纸，沿虚线对折一次得图②，再对折一次得图③，然后用

剪刀沿图③中的虚线剪去一个角，再打开后的形状是（    ）

①                ②             ③

A．         B．        C．        D．

⑶ 将一正方形纸片按图中①、②的方式依次对折后，再沿③中的虚线裁剪，最后将④中的纸

片打开铺平，所得图案应该是下面图案中的（    ）

①                ②          ③         ④

A．    B．      C．       D．

（人大附中期末）

【解析】       ⑴ C；⑵ C；⑶ B．

【点评】       既可以亲自剪裁，又可以按照折纸的先后顺序逐步倒推.

【例7】         ⑴ 如图，将一长方形纸片按图折叠，AE、DE为折痕，

，则度数为        ．

⑵ 当身边没有量角器时，怎样得到一些特定度数的角呢？动手操作有时可以解“燃眉之急”．如图，已知矩形ABCD，我们按如下步骤操作可以得到一个特定的角：

①以点A所在直线为折痕，折叠纸片，使点B落在AD上，折痕与BC交于E；

②将纸片展平后，再一次折叠纸片，以E所在直线为折痕，使点A落在BC上，折痕EF交AD于F．则=             .

【解析】       ⑴ ；⑵ ．

训练1.  对于大于或等于2的自然数n的平方进行如下“分裂”，分裂成n个连续奇数的和，则自然数72的分裂数中最大的数是     ，自然数n的分裂数中最大的数是     .

（通州区一模）

【解析】       13， 2n－1．

训练2.  如下图是某同学在沙滩上用石子摆成的小房子，观察图形的变化规律，写出第个小房子用了              块石子．

【解析】       ．

训练3.  如图，把一张长方形纸片对折，折痕为，以的中点为顶点把平角三等分，沿平角的三等分线折叠，将折叠的图形剪出一个以为顶点的等腰三角形，那么剪出的等腰三角形全部展开平铺后得到的平面图形一定是（    ）．

A．正三角形     B．正方形      C．正五边形        D．正六边形

【解析】       D.

【点评】       既可以亲自剪裁，又可以按照折纸的先后顺序逐步倒推．

训练4.  图⑴是一个水平摆放的小正方体木块，图⑵、⑶是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，至第七个叠放的图形中，小正方体木块总数应是         ．

【解析】       91．

题型一  探索图形规律  巩固练习

【练习1】   用同样规格的黑白两种颜色的正方形瓷砖，按下图的方式铺地板，则第个图形中有黑色

瓷砖      块，第个图形中需要黑色瓷砖        块（用含有的整式表示）．

【解析】       ，．

【练习2】   观察下列图形及图形所对应的算式，根据你发现的规律计算（是正

整数）的结果为（     ）                                                       

A．        B．        C．        D．

【解析】      A．

【练习3】   图1是棱长为的小正方体，图2、图3由这样的小正方体摆放而成．按照这样的方法

继续摆放，由上而下分别叫第一层、第二层、…、第层，第层的小正方体的个数为．解答下列问题：

① 按照要求填表：

② 写出当时，           ．

【解析】       ① ；

②.

题型二  实验与操作 巩固练习

【练习4】   如图所示，将一张正方形纸片对折两次，然后在上面打个洞，则纸片展开后是（    ）

【解析】       D．

【练习5】   如图，一个的矩形可以用种不同的方式分割成或或个小正方形，那么一个

的矩形用不同的方式分割后，小正方形的个数可以是           ．

【解析】       4或7或9或12或15．