2007年全国初中数学联合竞赛试题及详细解答(含一试二试)

2007年全国初中数学联合竞赛试题

第一试

一、选择题（本题满分42分，每小题7分）

本题共有6小题，每题均给出了代号为的四个答案，其中有且仅有一个是正确的.将你所选择的答案的代号填在题后的括号内.每小题选对得7分；不选、选错或选出的代号字母超过一个（不论是否写在括号内），一律得0分.

1. 已知满足，则的值为                     （    ）

（A）1.         （B）.         （C）.         （D）.

2．当分别取值，，，…，，，，…，，，时，计算代数式的值，将所得的结果相加，其和等于                              （     ）

（A）－1.       （B）1.        （C）0.       （D）2007.

3. 设是△的三边长，二次函数在时取最小值，则△是                                                        （    ）

（A）等腰三角形.     （B）锐角三角形.      （C）钝角三角形.     （D）直角三角形.

4. 已知锐角△的顶点到垂心的距离等于它的外接圆的半径，则∠的度数是（    ）

（A）30°.        （B）45°.        （C）60°.        （D）75°

.

5．设是△内任意一点，△、△、△的重心分别为、、，则的值为                                                         （    ）

（A）.         （B）.         （C）.         （D）.

6．袋中装有5个红球、6个黑球、7个白球，从袋中摸出15个球，摸出的球中恰好有3个红球的概率是                                                                      （    ）

（A）.          （B）.         （C）.         （D）.

二、填空题（本题满分28分，每小题7分）

1. 设，是的小数部分，是的小数部分，则______.

2. 对于一切不小于2的自然数，关于的一元二次方程的两个根记作（），则=   

3. 已知直角梯形的四条边长分别为，过、两点作圆,与的延长线交于点，与的延长线交于点，则的值为______.

.

4． 若和均为四位数，且均为完全平方数，则整数的值是______

第二试 （A）

一、 （本题满分20分）设为正整数，且，如果对一切实数，二次函数的图象与轴的两个交点间的距离不小于，求的值.

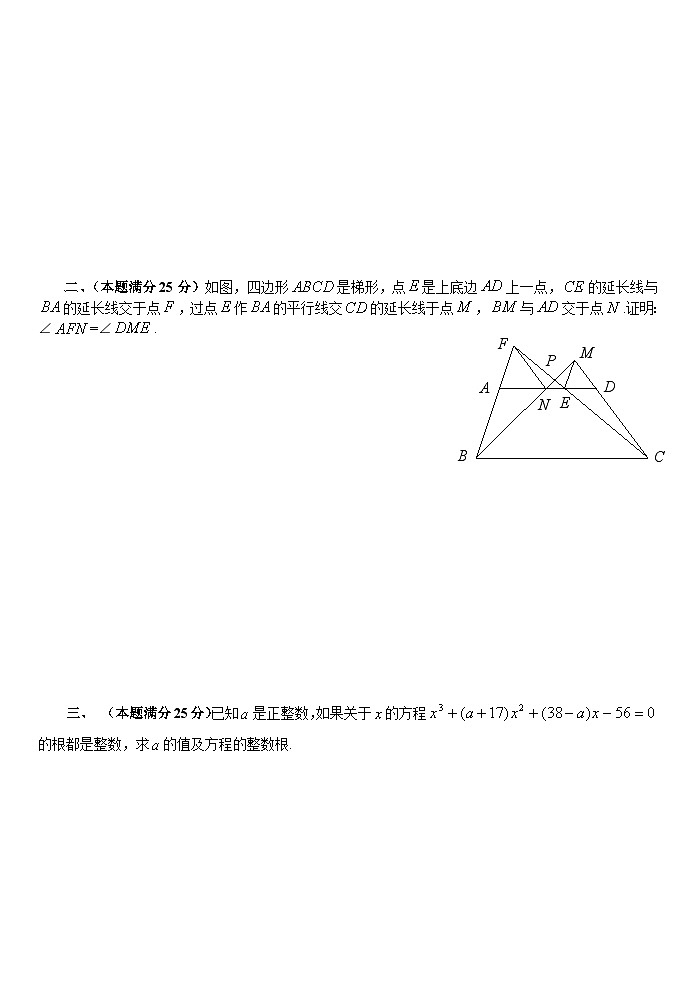
二、（本题满分25分）如图，四边形是梯形，点是上底边上一点，的延长线与的延长线交于点，过点作的平行线交的延长线于点，与交于点.证明：∠=∠.

三、 （本题满分25分）已知是正整数，如果关于的方程的根都是整数，求的值及方程的整数根.

第二试 （B）

一、（本题满分20分）设为正整数，且，二次函数的图象与轴的两个交点间的距离为，二次函数的图象与轴的两个交点间的距离为.如果对一切实数恒成立，求的值

二、（本题满分25分）题目和解答与（A）卷第二题相同.

.

三、（本题满分25分）设是正整数，二次函数，反比例函数，如果两个函数的图象的交点都是整点（横坐标和纵坐标都是整数的点），求的值.

第二试 （C）

一、（本题满分25分）题目和解答与（B）卷第一题相同.

二、（本题满分25分）题目和解答与（A）卷第二题相同.

三、（本题满分25分）设是正整数，如果二次函数和反比例函数的图象有公共整点（横坐标和纵坐标都是整数的点），求的值和对应的公共整点.

2007年全国初中数学联合竞赛

试题参考答案及评分标准

说明：评阅试卷时，请依据本评分标准.第一试，选择题和填空题只设7分和0分两档；第二试各题，请严格按照本评分标准规定的评分档次给分，不要再增加其他中间档次.如果考生的解答方法和本解答不同，只要思路合理，步骤正确，在评卷时请参照本评分标准划分的档次，给予相应的分数.

第一试

一、选择题（本题满分42分，每小题7分）

本题共有6小题，每题均给出了代号为的四个答案，其中有且仅有一个是正确的.将你所选择的答案的代号填在题后的括号内.每小题选对得7分；不选、选错或选出的代号字母超过一个（不论是否写在括号内），一律得0分.

1. 已知满足，则的值为                      （    ）

（A）1.         （B）.         （C）.         （D）.

【答】B.

解  由得，所以，故选（B）.

注：本题也可用特殊值法来判断.

2．当分别取值，，，…，，，，…，，，时，计算代数式的值，将所得的结果相加，其和等于                        （     ）

（A）－1.       （B）1.        （C）0.       （D）2007.

【答】C.

解  因为，即当分别取值，为正整数）时，计算所得的代数式的值之和为0；而当时，.因此，当分别取值，，，…，，，，…，，，时，计算所得各代数式的值之和为0.故选（C）.

3. 设是△的三边长，二次函数在时取最小值，则△是                                                      （    ）

（A）等腰三角形.     （B）锐角三角形.      （C）钝角三角形.     （D）直角三角形.

【答】D.

解  由题意可得即所以，，因此，所以△是直角三角形. 故选（D）.

4. 已知锐角△的顶点到垂心的距离等于它的外接圆的半径，则∠的度数是（    ）

（A）30°.        （B）45°.        （C）60°.        （D）75°.

【答】C.

解  锐角△的垂心在三角形内部，如图，设△的外心为，为的中点，的延长线交⊙于点，连、，则//，//，则，所以∠＝30°，∠＝60°，所以∠＝∠＝60°.故选（C）.

5．设是△内任意一点，△、△、△的重心分别为、、，则的值为                                                  （    ）

（A）.         （B）.         （C）.         （D）.

【答】A.

解  分别延长、、，与△的三边、、交于点、、，由于、、分别为△、△、△的重心，易知、、分别为、、的中点，所以.

易证△∽△，且相似比为，所以.

所以.故选（A）.

6．袋中装有5个红球、6个黑球、7个白球，从袋中摸出15个球，摸出的球中恰好有3个红球的概率是  （    ）

（A）.          （B）.         （C）.         （D）.

【答】B.

解  设摸出的15个球中有个红球、个黑球、个白球，则都是正整数，且，.因为，所以可取值2，3，4，5.

当时，只有一种可能，即；

当时，，有2种可能，或；

当时，，有3种可能，或或；

当时，，有4种可能，或或或.

因此，共有1＋2＋3＋4＝10种可能的摸球结果，其中摸出的球中恰好有3个红球的结果有2种，所以所求的概率为.故选（B）.

二、填空题（本题满分28分，每小题7分）

1. 设，是的小数部分，是的小数部分，则____1___.

解  ∵，而，∴.

又∵，而，∴.∴，

∴.

2. 对于一切不小于2的自然数，关于的一元二次方程的两个根记作（），

则=

解  由根与系数的关系得，，所以

，

则，

＝.

3. 已知直角梯形的四条边长分别为，过、两点作圆,与的延长线交于点，与的延长线交于点，则的值为____4_____.

解  延长交⊙于点，设的中点分别为点，则易知.因为，由割线定理，易证，所以.

4． 若和均为四位数，且均为完全平方数，则整数的值是___17____.

解 设，，则，两式相减得

，因为101是质数，且，所以，故.代入，整理得，解得，或（舍去）.

所以.

第二试 （A）

一、 （本题满分20分）设为正整数，且，如果对一切实数，二次函数的图象与轴的两个交点间的距离不小于，求的值.

解  因为一元二次方程的两根分别为和，所以二次函数的图象与轴的两个交点间的距离为.

由题意，，即，即.

由题意知，，且上式对一切实数恒成立，所以

所以或

二、（本题满分25分）如图，四边形是梯形，点是上底边上一点，的延长线与的延长线交于点，过点作的平行线交的延长线于点，与交于点.证明：∠=∠.

证明  设与交于点，∵//，

∴△∽△，∴,

∴.

又∵//，∴△∽△，∴,

∴.

∴,故

又∠=∠，∴△PNF∽△PMC，∴∠PNF＝∠PMC，∴NF//MC

∴∠ANF＝∠EDM.

又∵ME//BF，∴∠FAN＝∠MED.

∴∠ANF＋∠FAN＝∠EDM＋∠MED，∴∠AFN=∠DME.

三、 （本题满分25分）已知是正整数，如果关于的方程的根都是整数，求的值及方程的整数根.

解  观察易知，方程有一个整数根，将方程的左边分解因式，得

因为是正整数，所以关于的方程

                                   （1）

的判别式，它一定有两个不同的实数根.

而原方程的根都是整数，所以方程（1）的根都是整数，因此它的判别式应该是一个完全平方数.

设（其中为非负整数），则，即

.

显然与的奇偶性相同，且，而，所以

或或解得或或

而是正整数，所以只可能或

当时，方程（1）即，它的两根分别为和.此时原方程的三个根为1，和.

当时，方程（1）即，它的两根分别为和.此时原方程的三个根为1，和.

第二试 （B）

一、（本题满分20分）设为正整数，且，二次函数的图象与轴的两个交点间的距离为，二次函数的图象与轴的两个交点间的距离为.如果对一切实数恒成立，求的值.

解  因为一元二次方程的两根分别为和，所以；

一元二次方程的两根分别为和，所以.

所以，

         （1）

由题意知，，且（1）式对一切实数恒成立，所以

所以或

二、（本题满分25分）题目和解答与（A）卷第二题相同.

三、（本题满分25分）设是正整数，二次函数，反比例函数，如果两个函数的图象的交点都是整点（横坐标和纵坐标都是整数的点），求的值.

解  联立方程组消去得，即

，分解因式得

           （1）

显然是方程（1）的一个根，（1，56）是两个函数的图象的一个交点.

因为是正整数，所以关于的方程

                                        （2）

的判别式，它一定有两个不同的实数根.

而两个函数的图象的交点都是整点，所以方程（2）的根都是整数，因此它的判别式应该是一个完全平方数.

设（其中为非负整数），则，即

.

显然与的奇偶性相同，且，而，所以

或或解得或或

而是正整数，所以只可能或

当时，方程（2）即，它的两根分别为和，此时两个函数的图象还有两个交点和.

当时，方程（2）即，它的两根分别为和，此时两个函数的图象还有两个交点和.

第二试 （C）

一、（本题满分25分）题目和解答与（B）卷第一题相同.

二、（本题满分25分）题目和解答与（A）卷第二题相同.

三、（本题满分25分）设是正整数，如果二次函数和反比例函数的图象有公共整点（横坐标和纵坐标都是整数的点），求的值和对应的公共整点.

解  联立方程组消去得＝

，即，分解因式得

            （1）

如果两个函数的图象有公共整点，则方程（1）必有整数根，从而关于的一元二次方程

                                            （2）

必有整数根，所以一元二次方程（2）的判别式应该是一个完全平方数，

而.

所以应该是一个完全平方数，设（其中为非负整数），则，即.

显然与的奇偶性相同，且，而，所以

或或解得或或

而是正整数，所以只可能或

当时，方程（2）即，它的两根分别为2和，易求得两个函数的图象有公共整点和.

当时，方程（2）即，它的两根分别为1和，易求得两个函数的图象有公共整点和.