

2023年辽宁省锦州市中考数学一模试卷(含解析)
展开2023年辽宁省锦州市中考数学一模试卷
一、选择题(本大题共8小题,共16.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列实数中最小的数是( )
A. B. C. D.
2. 石墨烯具有优异的光学、电学、力学特性,在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景,被认为是一种未来革命性的材料,石墨烯中每两个相邻碳原子间的键长为米,数字“”用科学记数法表示为( )
A. B. C. D.
3. 由五个相同的立方体搭成的几何体如图所示,则它的左视图是( )
A.
B.
C.
D.
4. 下列运算正确的是( )
A. B.
C. D.
5. 今年月份某校举行学雷锋志愿服务活动,为了解全校学生一周学雷锋志愿服务的次数,随机抽取了名学生进行调查,依据调查结果绘制了如图所示的折线统计图,下列关于该校学生一周学雷峰志愿服务次数说法正确的是( )
A. 众数是 B. 中位数是 C. 中位数是 D. 众数是
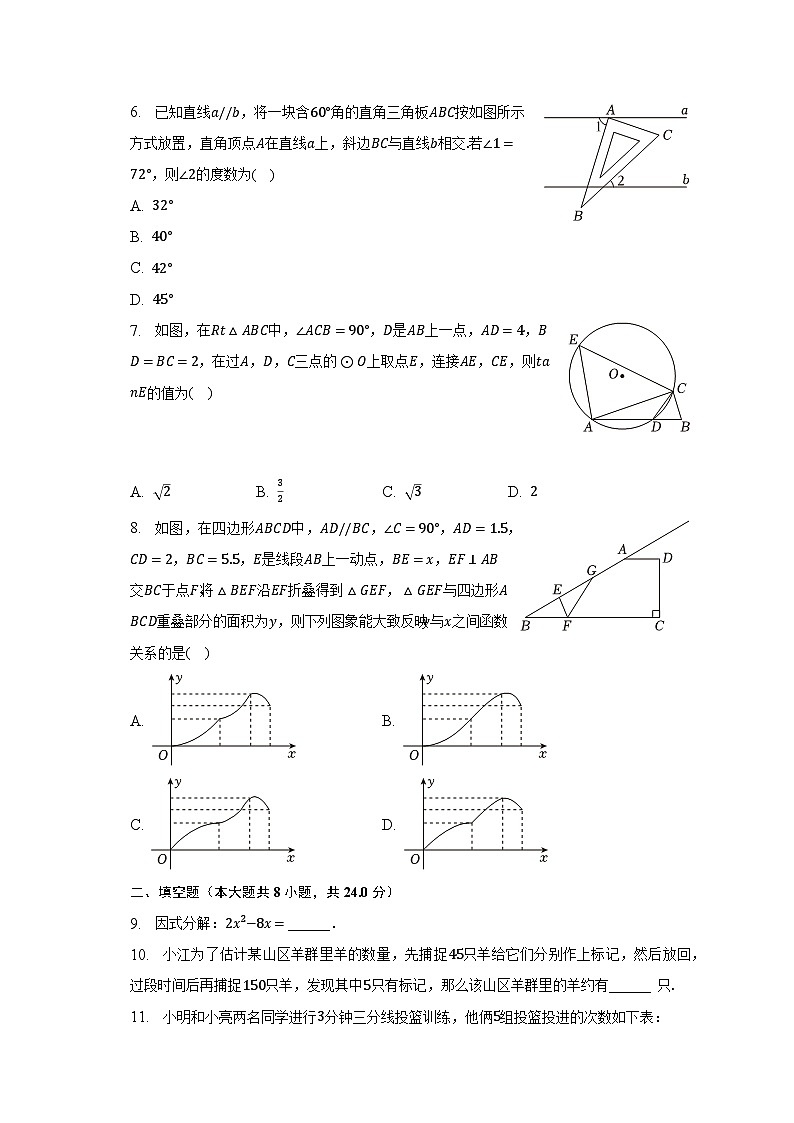
6. 已知直线,将一块含角的直角三角板按如图所示方式放置,直角顶点在直线上,斜边与直线相交若,则的度数为( )
A.
B.
C.
D.
7. 如图,在中,,是上一点,,,在过,,三点的上取点,连接,,则的值为( )
A. B. C. D.
8. 如图,在四边形中,,,,,,是线段上一动点,,交于点,将沿折叠得到,与四边形重叠部分的面积为,则下列图象能大致反映与之间函数关系的是( )
A. B.
C. D.
二、填空题(本大题共8小题,共24.0分)
9. 因式分解:______.
10. 小江为了估计某山区羊群里羊的数量,先捕捉只羊给它们分别作上标记,然后放回,过段时间后再捕捉只羊,发现其中只有标记,那么该山区羊群里的羊约有______ 只
11. 小明和小亮两名同学进行分钟三分线投篮训练,他俩组投篮投进的次数如下表:
小明投进的次数 | |||||
小亮投进的次数 |
小明和小亮组投篮训练投进次数的方差分别为;,则 ______ 填“”、“”或“”.
12. 关于的一元二次方程有两个不相等的的实数根,则的取值范围是______.
13. 如图,在菱形中,,以点为圆心,长为半径作弧,交于点,再分别以点,为圆心,大于长为半径作弧,两弧交于点,,作直线分别交,,于点,,,连接,,则 ______ .
14. 如图,是正方形的对角线上一点,,,垂足分别为点,若,,则的长是______ .
15. 如图,矩形的顶点,分别在轴,轴的正半轴上,点在第一象限,反比例函数的图象交矩形的对角线于点,分别交,于点,,连接,若,,则 ______ .
16. 如图,在平面直角坐标系中,四边形,,,都是菱形,点,,,,都在轴上,点,,,都在直线上,且,,则点的坐标是______ .
三、解答题(本大题共9小题,共80.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
先化简,再求值,其中.
18. 本小题分
家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康某市药监部门为了解市民家庭处理过期药品的方式,对全市家庭作一次简单的随机抽样调查,调查问卷中有六个选项:直接抛弃;卖给药贩;直接焚烧;送回收点;放置家中:继续使用被调查的家庭从中选取一项
下列选取样本的方法最合理的一种是______ ;只需填写正确答案的序号
在全市医务工作者中以家庭为单位随机抽取;
在全市常住人口中以家庭为单位随机抽取;
在市中心某个居民区以家庭为单位随机抽取.
药监部门对所有抽样得到的数据进行整理,得到下列统计表和扇形统计图:
种类 | 频数户数 |
直接抛弃 | |
卖给药贩 | |
直接焚烧 | |
送回收点 | |
放置家中 | |
继续使用 |
请根据统计图表,解答下列问题: ______ , ______ ;
请补全扇形统计图;
家庭过期药品的正确处理方式是送回收点,若该市有万户家庭,请估计有多少户家庭处理过期药品的方式是正确的.
19. 本小题分
乘坐高铁已经成为人们远行的主要方式高铁车厢的二等座一排有五个座位,座位布局采用模式一边座一边座,座位号分别是,,,,,其中,这两个座位是靠窗的张红妈妈准备到北京出差,如果她同时随机地购买了往返的车票,请用列表法或画树图的方法,求她往返都买到靠窗座位的概率.
20. 本小题分
某学校要对教室环境进行美化,准备购买,两种花卉装饰已知盆种花卉比盆种花卉便宜元:用元购买种花卉与用元购买种花卉的数量相等.
求,两种花卉的单价各是多少元?
该学校准备购买,两种花卉共盆,所需费用不超过元,那么至少购买种花卉多少盆?
21. 本小题分
如图,某工厂坐落在东西方向公路的北侧,,分别是矩形生产车间的入口和出口,车间宽度,生产出来的产品沿北偏西的厂内道路运送到库房存放,,工厂大门在库房南偏西的方向,求大门与车间入口之间的距离的长点,,,在直线上参考数据:,,,,,
22. 本小题分
如图,点在以为直径的上,延长到点,连接,过点作,交的延长线于点,交于点,连接,,若.
求证:是的切线;
若,求的长.
23. 本小题分
某体育用品商店销售一款排球,进价为元个,销售过程中发现,每天的销量个与销售单价元之间的关系可以近似地看作一次函数.
销售单价定为多少元时,每天可获利元?
写出每天获得的利润元与销售单价元之间的函数关系式,并求体育用品商店日销售的最大利润.
24. 本小题分
初步认识
如图,在四边形中,,连接,,过点作交的延长线于点求证:;
特例研究
如图,若四边形中,,中的其它条件不变,取,的中点,,连接.
求证:;
为的中点,连接,猜想与的位置关系,并证明你的猜想.
拓展应用
如图,在矩形中,对角线,相交于点,是射线上一动点,过点作交射线于点,当,,时,请直接写出的长.
25. 本小题分
如图,在平面直角坐标系中,抛物线与轴交于点,,与轴交于点经过点的直线交抛物线于点,点与点的横坐标互为相反数,是抛物线上一动点,连接.
求抛物线的表达式;
若点在第一象限内的抛物线上,当时,求直线的表达式;
点在轴上,若∽,请直接写出点的坐标.
答案和解析
1.【答案】
【解析】解:在,,,四个数中,
A、,、,
,
最小的数是,
故选:.
首先依据正号、负号比较大小,再依据同号比较大小即可.
此题主要考查了实数大小比较,掌握实数大小比较的方法是解答本题的关键.
2.【答案】
【解析】解:.
故选:.
绝对值小于的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为,其中,为由原数左边起第一个不为零的数字前面的的个数所决定.
3.【答案】
【解析】解:从左边看第一层是三个小正方形,第二层左边一个小正方形,
故选:.
根据从左边看得到的图形是左视图,可得答案.
本题考查了简单组合体的三视图,从左边看得到的图形是左视图.
4.【答案】
【解析】解:,
故A不符合题意;
,
故B不符合题意;
,
故C不符合题意;
,
故D符合题意,
故选:.
根据幂的乘方与积的乘方,合并同类项,完全平方公式,同底数幂的乘法运算分别判断即可.
本题考查了幂的乘方与积的乘方,合并同类项,完全平方公式,同底数幂的乘法,熟练掌握这些知识是解题的关键.
5.【答案】
【解析】解:因为出现了次,出现的次数最多,所以该校一周学雷峰志愿服务次数的众数是;
该校一周学雷峰志愿服务次数最中间的两个数字都为,所以该组数据的中位数为;
故选项A正确,符合题意.
故选:.
从折线图统计中获取信息,通过折线统计图和中位数、众数的定义等知识求解.
本题考查折线统计图、众数及中位数的定义等知识点,掌握众数、中位数的定义,并能从统计图中得到必要的信息是解决本题的关键.
6.【答案】
【解析】解:如图,
,,
,
,,
,
,
,
故选:.
根据平行线的性质得出,根据对顶角性质得出,根据三角形外角性质求解即可.
此题考查了平行线的性质,熟记“两直线平行,内错角相等”是解题的关键.
7.【答案】
【解析】解:延长交于点,连接,
,
,
,
,
四边形为的内接四边形,
,,
,
,
,,
,
,,
,
,
,
故选:.
延长交于点,连接,证出,,得出,由等腰三角形的判定得出,求出的长,根据锐角三角函数的定义可得出答案.
本题考查了圆周角定理,勾股定理,圆内接四边形的性质,解直角三角形,熟练掌握圆内接四边形的性质是解题的关键.
8.【答案】
【解析】解:当点运动不超过中点,即在四边形内部时,
过点作于点,
则,,,
所以.
在中,,.
则,故EF,
所以.
据此可以排除掉、.
当点超过中点时,
因为,则,
又,则∽,
所以,得.
又,则,
得.
所以,
即.
据此可以排除掉,
所以正确答案是B.
故选:.
先求出当点在不超过中点时的情况,再求超过中点但未超过点时的情况即可.
本题是一道动点函数图象题,得出重合部分的面积与的函数表达式是解题的关键.
9.【答案】
【解析】解:.
故答案为:.
直接提取公因式,进而分解因式得出答案.
此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.
10.【答案】
【解析】解:只,
所以该山区羊群里的羊约有只.
故答案为:.
用除以第二次捕捉只羊中有标志的羊所占的百分比即可.
此题考查了用样本估计总体,关键是求出有标志的羊所占的比,统计的思想就是用样本的信息来估计总体的信息,本题体现了统计思想.
11.【答案】
【解析】解:小明投进的次数的平均数为,
小明的方差分别为,
小亮投进的次数的平均数为,
小亮的方差分别为,
.
故答案为:.
分别计算出方差即可得出答案.
本题考查了方差,熟练掌握方差的计算公式是关键.
12.【答案】
【解析】解:关于的一元二次方程有两个不相等的实数根,
,
解得:.
故答案为:.
根据根的判别式和已知条件得出,再求出不等式的解集即可.
本题考查了根的判别式和解一元一次不等式,注意:已知一元二次方程、、为常数,,当时,方程有两个不相等的实数根,当时,方程有两个相等的实数根,当时,方程没有实数根.
13.【答案】
【解析】解:四边形为菱形,
,,
由作法得,垂直平分,
,,
,,
.
故答案为:.
先根据菱形的性质得到,,再利用基本作图得到,垂直平分,则,,接着利用等腰三角形的性质和三角形内角和得到,,然后计算即可.
本题考查了作图基本作图:熟练掌握种基本作图是解决问题的关键.也考查了线段垂直平分线的性质和菱形的性质.
14.【答案】
【解析】解:如图,连接,
是正方形的对角线,
,,
在和中,
,
≌,
,
,,
,
,
四边形是矩形,
,
根据勾股定理得,,
,
.
故答案为:.
连接,先用正方形的性质得出结论,判断出,≌,得出,然后判断出四边形是矩形,用勾股定理求出即可.
本题主要考查了正方形的性质,全等三角形的判定和性质,勾股定理,矩形的判定和性质,解本题的关键是判断出.
15.【答案】
【解析】解:作于,连接、,
,
∽,
,
::::,
设,,
,,
,,
由反比例函数的几何意义得,,
,
,
,,
,
,
即,
,
.
故答案为:.
作于,连接、,设点坐标,表示出三角形和三角形的面积,利用相似表示出矩形面积,由::,得出四边形的面积为,再列出方程解答即可.
本题考查了反比例函数的图形及性质的应用,几何意义的应用、矩形的性质、三角形相似等知识点是解题关键.
16.【答案】
【解析】解:直线,
当时,,
设直线与轴的交点为,则点的坐标为,
,
,,
,
同理可得,
,,,
,
的横坐标是:,纵坐标是:,
由此推出.
故答案为:
根据题意和图形可以求得前几个菱形的边长,然后根据锐角三角函数即可求得点的坐标.
本题考查菱形的性质,解直角三角形,根据已知点的变化规律求出菱形的边长,找出规律是解题的关键.
17.【答案】解:原式
,
当时,
原式
.
【解析】先根据分式的混合运算顺序和运算法则化简原式,再将的值代入计算即可.
本题主要考查了分式的化简求值,掌握分式混合运算顺序和运算法则是关键.
18.【答案】
【解析】解:在全市常住人口中以家庭为单位随机抽取具有代表性,
故答案为:;
由题意可知,样本容量为:,
故,,
故答案为:,;
直接抛弃所占百分比为:,
补全扇形统计图如下:
万户,
答:估计约万户家庭处理过期药品的方式是正确的.
根据抽样调查的样本要具有代表性和广泛性可得答案;
用的频数除以可得样本容量,再根据“频数总数频率”可得、的值;
求出所占百分百即可补全扇形统计图;
用万乘所占百分比可得答案.
本题考查了扇形统计图,用样本估计总体,频数分布表,利用“频数频率总数”求出样本容量是解答本题的关键.
19.【答案】解:画树状图如下:
共有种等可能的结果,其中张红妈妈往返都买到靠窗座位的结果有种,即、、、,
张红妈妈往返都买到靠窗座位的概率为.
【解析】画树状图,共有种等可能的结果,其中张红妈妈往返都买到靠窗座位的结果有种,再由概率公式求解即可.
此题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
20.【答案】解:设种花卉的单价是元,则种花卉的单价是元,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意,
.
答:种花卉的单价是元,种花卉的单价是元;
设购买种花卉盆,则购买种花卉盆,
根据题意得:,
解得:,
的最小值为.
答:至少购买种花卉盆.
【解析】设种花卉的单价是元,则种花卉的单价是元,利用数量总价单价,结合用元购买种花卉与用元购买种花卉的数量相等,可得出关于的分式方程,解之经检验后,可得出种花卉的单价,再将其代入中,即可求出种花卉的单价;
设购买种花卉盆,则购买种花卉盆,利用总价单价数量,结合所需费用不超过元,可得出关于的一元一次不等式,解之取其中的最小值,即可得出结论.
本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:找准等量关系,正确列出分式方程;根据各数量之间的关系,正确列出一元一次不等式.
21.【答案】解:过作于,延长交于,
则四边形是矩形,
,,
在中,,,,
,,
,,
在中,,,
,
,
答:大门与车间入口之间的距离的长约为.
【解析】过作于,延长交于,根据矩形的性质得到,,解直角三角形即可得到结论.
本题考查了解直角三角形的应用方向角问题,正确地作出辅助线是解题的关键.
22.【答案】证明:连接、交于点,连接,
是的直径,,
,
,
,
,
,
,
,
垂直平分,
,
是的直径,,
是的切线.
解:,
,
,
,,
,
,
,,
,
的长是.
【解析】连接、交于点,连接,由是的直径,,得,则,所以,而,所以,则,所以,则垂直平分,所以,即可证明是的切线;
由,得,则,因为,所以,则,,由勾股定理得,所以.
此题重点考查切线的判定、圆周角定理、垂径定理、勾股定理、锐角三角函数与解直角形等知识,正确地作出所需要的辅助线是解题的关键.
23.【答案】解:由题意可知,,
,
解得,或,
,
,
销售单价定为元时,每天可获利元;
由题意可知,,
,
当时,随的增大而增大,
当时,的最大值为元.
【解析】根据题意列出一元二次方程,解之即可得出结论;
根据利润销售量销售单价成本列出函数关系式,再根据二次函数的性质可得出结论.
本题考查的是二次函数在实际生活中的应用,关键是根据题意求出二次函数的解析式以及利用二次函数的性质求出最值.
24.【答案】证明:,
,
,
,
,
;
证明:,
,
即.
,
由知,
≌,
,
,分别是,的中点,
是的中位线,
,
;
解:.
证明:连接,,
由知,≌,
,
,,
和都是等腰直角三角形.
,,
,
又为中点,为中点,
,,
,
∽,
,,
,,
∽,
,
,
,
;
解:当点在线段的延长线上时,过点作于点,于点,与交于点,如图,
,,
,
四边形是矩形,
,,
,
四边形是矩形,
,,,
,
为的中点,
,
同理,
,,
,
又,
∽,
,
,
,
;
当点在线段上时,过点作于点,于点,如图,
同理可得∽,
,
,
,
,
综上所述,的长为或.
【解析】由直角三角形的性质可得出结论;
由知,证明≌,由全等三角形的性质得出,由三角形中位线定理得出则可得出结论;
连接,,证明∽,由相似三角形的性质得出,,证明∽,由相似三角形的性质得出,则可得出结论;
当点在线段的延长线上时,过点作于点,于点,与交于点,证明∽,由相似三角形的性质得出,求出的长可得出答案;当点在线段上时,过点作于点,于点,同理可得出答案.
本题是四边形综合题,考查了相似三角形的判定与性质,矩形的判定与性质,三角形中位线定理,全等三角形的判定和性质,等腰直角三角形的性质,熟练掌握以上知识点是解题的关键.
25.【答案】解:对于,令,则,
设直线与轴的交点为点,则,
令,则,即点,
当时,,即点,
将点、的坐标代入抛物线表达式得:
,
解得:,
故抛物线的表达式为:;
由抛物线的表达式知,点,
如图,由知,点,则,
则,
则,
过点作于点,
由点、、的坐标知,,,,
则,
即,
解得:,
则,
则,
则直线的表达式为:;
当点在点的下方时,如图,
过点作轴的平行线交过点与轴的平行线于点,交过点和轴的平行线于点,
∽,则为直角,
,
,
,
,
∽,
∽,
则,即和的相似比为,
由点的坐标知,,设,则点的坐标为:,
则,,
则点的坐标为:,即,
将点的坐标代入抛物线表达式得:,
解得:负值已舍去,
即点的坐标为:;
当点在点的上方时,
同理可得,点的坐标为:,
将点的坐标代入抛物线表达式得:,
此方程无解.
综上,点的坐标为:
【解析】用待定系数法即可求解;
证明,得到,进而求解;
当点在点的下方时,利用∽,得到,即和的相似比为,求出点的坐标,进而求解;当点在点的上方时,同理可得.
本题是二次函数综合题,主要考查了一次函数的性质、解直角三角形、三角形相似等,其中,要注意分类求解,避免遗漏.
2023年辽宁省锦州市中考数学二模试卷(含解析): 这是一份2023年辽宁省锦州市中考数学二模试卷(含解析),共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年辽宁省锦州市中考数学试卷(含解析): 这是一份2023年辽宁省锦州市中考数学试卷(含解析),共29页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年辽宁省锦州市黑山县中考数学一模试卷(含解析): 这是一份2023年辽宁省锦州市黑山县中考数学一模试卷(含解析),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












