第三章《图形的相似》（提高卷）-2022-2023学年九年级数学上册章节复习全程检测通关练（讲义＋试题）（湘教版）

这是一份第三章《图形的相似》（提高卷）-2022-2023学年九年级数学上册章节复习全程检测通关练（讲义＋试题）（湘教版），文件包含第三章《图形的相似》提高卷原卷版docx、第三章《图形的相似》提高卷解析版docx等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。
第三章   图形的相似（提高卷）一、选择题（每小题4分，共40分） 1、若，则的值为(        ) A. B. C. D.【答案】B【解析】∵   ，   ∴   .
2、如果两个相似三角形的周长比是，那么它们的面积比是(        ) A. B. C. D.【答案】B【解析】因为两个相似三角形的周长比是，而相似三角形面积的比等于相似比的平方，
所以它们的面积比是．
3、下列各组条件中，一定能推得与相似的是(        ) A.且 B.且
C.且 D.且
【答案】C【解析】，和不是两个三角形的对应角，故不能判定两三角形相似，故此选项错误；
，，都不是两个三角形的对应角，故不能判定两三角形相似，故此选项错误；
，由，，可以根据两组对应边的比相等且夹角对应相等的两个三角形相似可以判断出与相似，故此选项正确；
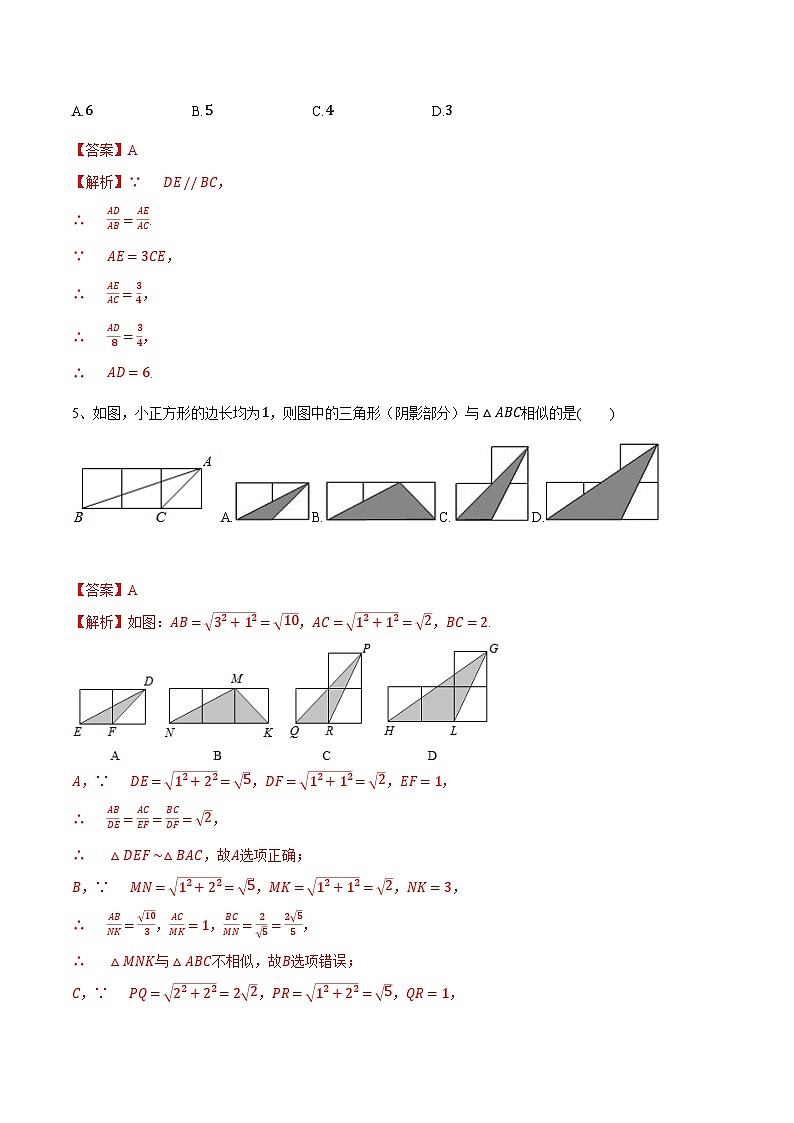
，且不能判定两三角形相似，因为相等的两个角不是夹角，故此选项错误.4、如图，，分别为，上的点，且，，，则的长为(        )
A. B. C. D.【答案】A【解析】∵   ，
∴   .
∵   ，
∴   ，
∴   ，
∴   .5、如图，小正方形的边长均为，则图中的三角形（阴影部分）与相似的是(        )
A.B.C.D.
 【答案】A【解析】如图：，，.

，∵   ，，，
∴   ，
∴   ，故选项正确；
，∵   ，，，
∴   ，，，
∴   与不相似，故选项错误；
，∵   ，，，
∴   ，，，
∴   与不相似，故选项错误；
，∵   ，，，
∴   ，，，
∴   与不相似，故选项错误．
6、如图，在平行四边形中，点是边的中点，交对角线于点，则等于(        )
  A. B. C. D.【答案】D【解析】在平行四边形中，
，
则，
∴   .
∵   点是边的中点，
∴   ，
∴   ．7、如图，小雅同学在利用标杆测量建筑物的高度时，测得标杆高，又知＝，则建筑物的高是（      ）
A. B. C. D.【答案】B【解析】∵   ＝，
∴   ＝，
∵   ，
∴   ，
∴   ，
∵   ＝，
∴   ＝，8、已知线段的长度为，点是线段的黄金分割点，则的长度为(        ) A. B.
C.或 D.以上结论都不对
【答案】C【解析】∵   线段，是线段的黄金分割点，
当，
∴   ；
当，
∴   ，
∴   ．
9、如图，已知和是以点为位似中心的位似图形，若点，，，，则点的对应点的坐标是(        )
A. B. C. D.【答案】B【解析】∵   点， ， ，，
∵   点是线段的中点，
∴   和是以点为位似中心的位似图形，
∴   ，
∴   点是线段的中点.
点，，
∴   点的对应点的坐标为.10、如图，正方形中，为中点，，，交于，交于，下列说法正确的有(        )个
①             ②        ③       ④
A. B. C. D.【答案】C【解析】如图所示，连接，

∵   四边形是正方形，
∴   ，.
∵   ，，
∴   ，
∴   ，
∴   .
∵   是的中点，，
∴   ，
∴   是等边三角形，
∴   ，
∴   ，
∴   ，故①错误；
∵   ，
∴   ，
∴   ，故②正确；
∵   ，，
∴   ，
∴   ，
∴   ，故③正确；
∵   ，
∴   ，，
∴   .
又∵   ，
∴   ，
∴   ，
∴   .
又∵   ，
∴   ，故④正确.
综上所述，②③④正确.
二、 填空题 （本题共计6小题，每题4分，共计24分） 11. 若，则________. 【答案】12. 两三角形的相似比是，则其面积之比是________． 【答案】13. 已知点是线段的黄金分割点，且，若，则________. 【答案】如图，在中，于．若，则________, ________,________.
【答案】,, 如图，与是以坐标原点为位似中心的位似图形，位似比为，＝，＝，若，则点的坐标为________．
【答案】 16. 如图，在三角形中， ，．点从沿以厘米秒的速度移动，点从沿以厘米秒的速度向移动．如果两点同时出发，经过________秒后， 与相似．
【答案】或三、解答题（本题共计8小题，每题10分，共计86分） 17、已知：＝  （1）求代数式的值；      （2）如果＝，求，，的值．【解析】（1）根据比例设＝，＝，＝，然后代入比例式进行计算即可得解；
（2）先设＝，＝，＝，然后将其代入＝，即可求得、、的值．【解答】∵   ＝，
∴   设＝，＝，＝，
则；设＝，＝，＝，则
＝，
解得＝．
则＝＝，
＝＝，
＝＝．18、如图，在每个小正方形边长为个单位长的网格中，建立直角坐标系，点，，均在格点上．

请在该网格内部画出，使其与关于点成位似图形，且位似比为；直接写出中点的坐标为________．【解析】（1）延长到，使，延长到，使，连接，可得出所求三角形；（2）根据图形确定出点的坐标即可．【解答】解：如图所示，为所求三角形.

根据得点的坐标为．
故答案为：.19、如图，在中，为上一点， ．
  求证： ；若，求的长．【答案】证明：，，
．解：，
，
，，
，
解得：，
．20、如图，、相交于点，且，，，，．  （1）与相似吗？（2）求的度数．【解析】（1）利用两边及其夹角法，可判断与相似；（2）根据相似三角形的性质可得的度数．【解答】解：（1）∵   ，，，
∴   ．（2）∵   ，
∴   ．21、如图，，与的交点为，．
  求证：；如果，，求，的长．【解析】（1）根据相似三角形的判定证明即可；
（2）利用相似三角形的性质解答即可．【解答】证明：∵   ，，
∴   .解：∵   ，
∴   ，
∴   .
∵   ，，
∴   .
∵   ，
∴   ，
∴   ，
∴   ． 22、如图，在中，点，分别在边，上，，．
  求证：；若，，求线段的长．【答案】证明：，
 ，
，
，
又，
．解：，
，
又，
，
，
，
．23、如图，中，＝厘米，＝厘米，点从出发，以每秒厘米的速度向运动，点从同时出发，以每秒厘米的速度向运动，其中一个动点到端点时，另一个动点也相应停止运动，设运动的时间为．
  （1）用含的代数式表示：＝________，＝________．（2）当以，，为顶点的三角形与相似时，求运动时间是多少？【解析】（1）利用速度公式求解；
（2）由于＝，利用相似三角形的判定，当时，，即；当时，，即，然后分别解方程即可．【解答】＝，＝．∵   ＝，
∴   当时，，即，解得；
当时，，即，解得＝．
∴   运动时间为秒或秒．
 24、如图，在中，，是边上的中线，于点，交于点，过点作交的延长线于点．
  求证：；求证：；若，，求的长．【答案】证明：，是边上的中线，
，，
，，
，
，
，
，
．证明：连接，如图，

，，
，
，
，
，
，
，
，
，
，
，
，
，
，
．连接，如图，

，，
，，
，
，
，
，
，
由得，
，
，
，
．