第2章 对称图形——圆（单元测试·基础卷）-2023-2024学年九年级数学上册基础知识专项突破讲与练（苏科版）

这是一份第2章 对称图形——圆（单元测试·基础卷）-2023-2024学年九年级数学上册基础知识专项突破讲与练（苏科版），共26页。

第2章 对称图形——圆（单元测试·基础卷）
【要点回顾】

圆



一、 单选题（本大题共10小题，每小题3分，共30分）
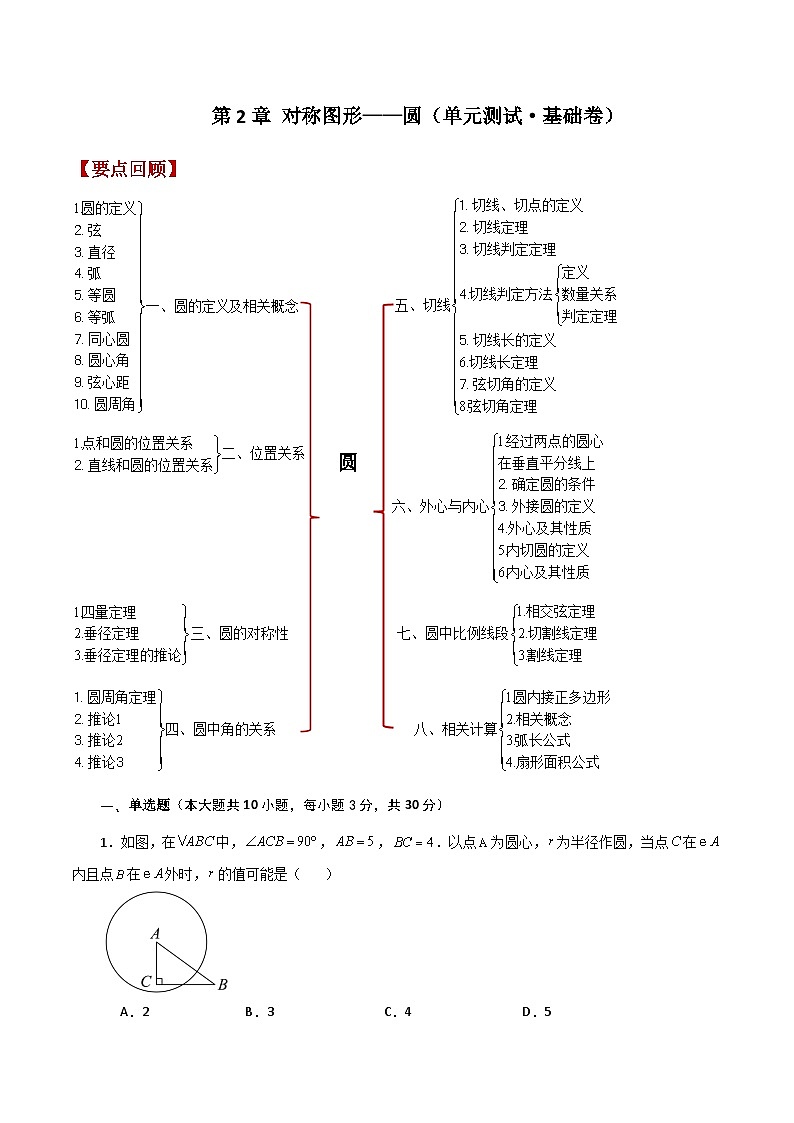
1．如图，在中，，，．以点为圆心，为半径作圆，当点在内且点在外时，的值可能是（    ）

A．2 B．3 C．4 D．5
2．已知平面内有和点，，若半径为，线段，，则直线与的位置关系为（      ）
A．相离 B．相交 C．相切 D．相交或相切
3．在中，直径弦于点若，则的长为（  ）

A． B．
C． D．
4．如图，点在上，，则（    ）

A． B． C． D．
5．如图，是锐角三角形的外接圆，，垂足分别为，连接．若的周长为21，则的长为（    ）
  
A．8 B．4 C．3.5 D．3
6．如图所示，是的直径，弦交于点E，连接，若，则的度数是（    ）
  
A． B． C． D．
7．如图，⊙O是等边△ABC的外接圆，若AB=3，则⊙O的半径是（    ）

A． B． C． D．
8．如图，AB是⊙O的直径，PA与⊙O相切于点A，∠ABC＝25°，OC的延长线交PA于点P，则∠P的度数是（   ）
  
A．25° B．35° C．40° D．50°
9．大自然中有许多小动物都是“小数学家”，如图1，蜜蜂的蜂巢结构非常精巧、实用而且节省材料，多名学者通过观测研究发现：蜂巢巢房的横截面大都是正六边形．如图2，一个巢房的横截面为正六边形，若对角线的长约为8mm，则正六边形的边长为（   ）

A．2mm B． C． D．4mm
10．如图，是等边的外接圆，点是弧上一动点（不与，重合），下列结论：①；②；③当最长时，；④，其中一定正确的结论有（    ）

A．1个 B．2个 C．3个 D．4个
二、 填空题（本大题共8小题，每小题4分，共32分）
11．如图，在平面直角坐标系中，点的坐标为，点在轴正半轴上，以点为圆心，长为半径作弧，交轴正半轴于点，则点的坐标为 ．

12．如图，在⊙O中，弦的长为4，圆心到弦的距离为2，则的度数为 ．

13．如图，点C、D分别是半圆AOB上的三等分点，若阴影部分的面积为，则半圆的半径OA的长为 ．

14．如图，四边形内接于，延长至点，已知，那么 ．
  
15．如图，某博览会上有一圆形展示区，在其圆形边缘的点处安装了一台监视器，它的监控角度是，为了监控整个展区，最少需要在圆形边缘上共安装这样的监视器 台．
  
16．如图，内接于是直径，过点A作的切线．若，则的度数是 度．

17．在中，若，，则的面积的最大值为 ．
18．如图，的半径为，为的弦，点为上的一点，将沿弦翻折，使点与圆心重合，则阴影部分的面积为 ．（结果保留与根号）

三、解答题（本大题共6小题，共58分）
19．（8分）如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC=CB，延长DA
与⊙O的另一个交点为E，连结AC，CE．
（1）求证：∠B=∠D；
（2）若AB=4，BC-AC=2，求CE的长．









20．（8分）如图，有一座拱桥是圆弧形，它的跨度米，拱高米，
（1）求圆弧所在的圆的半径r的长；
（2）当洪水泛滥到跨度只有30米时，要采取紧急措施，若拱顶离水面只有4米，即米是否要采取紧急措施？







21．（10分）如图，在中，，以为直径的交于点，过点作，垂足为点．
（1）求证：；
（2）判断直线与⊙O的位置关系，并说明理由．







22．（10分）如图，AB为⊙O的直径，F为弦AC的中点，连接OF并延长交于点D，过点D作⊙O的切线，交BA的延长线于点E．
（1）求证：AC∥DE；
（2）连接CD，若OA=AE=a，写出求四边形ACDE面积的思路．







23．（10分）已知为的直径，点C为上一点，点D为延长线一点，连接.
（Ⅰ）如图①，，若与相切，求和的大小；
（Ⅱ）如图②，与交于点E，于点F，连接，若，求的大小.







24．（12分）“抖空竹”在我国有着悠久的历史，是国家级的非物质文化遗产之一．小颖玩“抖空竹”游戏时发现可以将某时刻的情形抽象成数学问题．如图，，分别与相切于点，，延长，交于点，连接，，的半径为2，．
（1）连接，，判断四边形的形状，并说明理由；
（2）求劣弧的长；
（3）若某时刻，与交于点，求的长．
          





参考答案
1．C
【分析】先利用勾股定理可得，再根据“点在内且点在外”可得，由此即可得出答案．
解：在中，，，，
，
点在内且点在外，
，即，
观察四个选项可知，只有选项C符合，
故选：C．
【点拨】本题考查了勾股定理、点与圆的位置关系，熟练掌握点与圆的位置关系是解题关键．
2．D
【分析】根据点与圆的位置关系的判定方法进行判断．
解：∵⊙O的半径为2cm，线段OA=3cm，线段OB=2cm，
即点A到圆心O的距离大于圆的半径，点B到圆心O的距离等于圆的半径，
∴点A在⊙O外．点B在⊙O上，
∴直线AB与⊙O的位置关系为相交或相切，
故选：D．
【点拨】本题考查了直线与圆的位置关系，正确的理解题意是解题的关键．
3．C
【分析】先连接OD,然后利用垂径定理和勾股定理解答即可．
解：如图连接OD
∵直径AB＝15，
∴DO=BO＝7.5，
∵OC：OB＝3：5，
∴CO＝4.5，
∵DE⊥AB，
∴DC＝
∴DE＝2DC＝12．
故选：C．

【点拨】本题主要考查了垂径定理和勾股定理，正确作出辅助线并灵活运用垂径定理是解答本题的关键．
4．D
【分析】先证明再利用等弧的性质及圆周角定理可得答案．
解： 点在上，，


故选：
【点拨】本题考查的两条弧，两个圆心角，两条弦之间的关系，圆周角定理，等弧的概念与性质，掌握同弧或等弧的概念与性质是解题的关键．
5．B
【分析】根据三角形外接圆的性质得出点D、E、F分别是的中点，再由中位线的性质及三角形的周长求解即可．
解：∵是锐角三角形的外接圆，，
∴点D、E、F分别是的中点，
∴，
∵的周长为21，
∴即，
∴，
故选：B．
【点拨】题目主要考查三角形外接圆的性质及中位线的性质，理解题意，熟练掌握三角形外接圆的性质是解题关键．
6．D
【分析】如图所示，连接，先由同弧所对的圆周角相等得到，再由直径所对的圆周角是直角得到，则．
解：如图所示，连接，
∵，
∴，
∵是的直径，
∴，
∴，
故选D．
  
【点拨】本题主要考查了同弧所对的圆周角相等，直径所对的圆周角是直角，正确求出的度数是解题的关键．
7．C
【分析】作直径AD，连接CD，如图，利用等边三角形的性质得到∠B=60°，关键圆周角定理得到∠ACD=90°，∠D=∠B=60°，然后利用含30度的直角三角形三边的关系求解．
解：作直径AD，连接CD，如图，

∵△ABC为等边三角形，
∴∠B=60°，
∵AD为直径，
∴∠ACD=90°，
∵∠D=∠B=60°，则∠DAC=30°，
∴CD=AD，
∵AD2=CD2+AC2，即AD2=（AD）2+32，
∴AD=2，
∴OA=OB=AD=．
故选：C．
【点拨】本题考查了三角形的外接圆与外心：三角形外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心．也考查了等边三角形的性质、圆周角定理和含30度的直角三角形三边的关系．
8．C
【分析】根据圆周角定理可得，根据切线的性质可得，根据直角三角形两个锐角互余即可求解．
解：，∠ABC＝25°，
，
AB是⊙O的直径，
，
．
故选C．
【点拨】本题考查了圆周角定理，切线的性质，掌握圆周角定理与切线的性质是解题的关键．
9．D
【分析】如图，连接CF与AD交于点O，易证△COD为等边三角形，从而CD=OC=OD=AD，即可得到答案．
解：连接CF与AD交于点O，
∵为正六边形，
∴∠COD= =60°，CO=DO，AO=DO=AD=4mm，
∴△COD为等边三角形，
∴CD=CO=DO=4mm，
即正六边形的边长为4mm，
故选：D．

【点拨】本题考查了正多边形与圆的性质，正确把握正六边形的中心角、半径与边长的关系是解题的关键．
10．C
【分析】根据等边三角形的性质可得，从而得到∠ADB=∠BDC，故①正确；根据点是上一动点，可得不一定等于，故②错误；当最长时，DB为圆O的直径，可得∠BCD=90°，再由是等边的外接圆，可得∠ABD=∠CBD=30°，可得，故③正确；延长DA至点E，使AE=AD，证明△ABE≌△CBD，可得BD=AE，∠ABE=∠DBC，从而得到△BDE是等边三角形，可得到DE=BD，故④正确；即可求解．
解：∵△ABC是等边三角形，
∴AB=BC，∠ABC=60°，
∴，
∴∠ADB=∠BDC，故①正确；
∵点是上一动点，
∴不一定等于，
∴DA=DC不一定成立，故②错误；
当最长时，DB为圆O的直径，
∴∠BCD=90°，
∵是等边的外接圆，∠ABC=60°，
∴BD⊥AC，
∴∠ABD=∠CBD=30°，
∴，故③正确；
如图，延长DA至点E，使AE=DC，

∵四边形ABCD为圆O的内接四边形，
∴∠BCD+∠BAD=180°，
∵∠BAE+∠BAD=180°，
∴∠BAE=∠BCD，
∵AB=BC，AE=CD，
∴△ABE≌△CBD，
∴BD=AE，∠ABE=∠DBC，
∴∠ABE+∠ABD=∠DBC+∠ABD=∠ABC=60°，
∴△BDE是等边三角形，
∴DE=BD，
∵DE=AD+AE=AD+CD，
∴，故④正确；
∴正确的有3个．
故选：C．
【点拨】本题主要考查了圆周角定理，三角形的外接圆，圆内接四边形的性质，垂径定理，等边三角形的判定和性质等知识，熟练掌握圆周角定理，三角形的外接圆，圆内接四边形的性质，垂径定理，等边三角形的判定和性质等知识是解题的关键．
11．
【分析】连接，先根据点的坐标可得，再根据等腰三角形的判定可得是等腰三角形，然后根据等腰三角形的三线合一可得，由此即可得出答案．
解：如图，连接，

点的坐标为，
，
由同圆半径相等得：，
是等腰三角形，
，
（等腰三角形的三线合一），
又点位于轴正半轴，
点的坐标为，
故答案为：．
【点拨】本题考查了同圆半径相等、等腰三角形的三线合一、点坐标等知识点，熟练掌握等腰三角形的三线合一是解题关键．
12．
【分析】先根据垂径定理可得，再根据等腰直角三角形的判定与性质即可得．
解：由题意得：，，
，
，
，
是等腰直角三角形，
，
故答案为：．
【点拨】本题考查了垂径定理、等腰直角三角形的判定与性质，熟练掌握垂径定理是解题关键．
13．
【分析】如图，连接 证明再证明从而可以列方程求解半径．
解：如图，连接
点C、D分别是半圆AOB上的三等分点，


为等边三角形，



  


解得： （负根舍去），
故答案为：

【点拨】本题考查的圆的基本性质，弧，弦，圆心角之间的关系，平行线的判定与性质，扇形面积的计算，掌握以上知识是解题的关键．
14．
【分析】根据圆周角定理得到，再根据圆内接四边形性质和平角的定义即可得解．
解：∵，
∴，
∵四边形内接于，
∴，
∵，
∴，
故答案为：．
【点拨】此题考查了圆内接四边形的性质、圆周角定理，熟记圆内接四边形的性质、圆周角定理是解题的关键．
15．4
【分析】圆周角定理求出对应的圆心角的度数，利用圆心角的度数即可得解．
解：∵，
∴对应的圆心角的度数为，
∵，
∴最少需要在圆形边缘上共安装这样的监视器台；
故答案为：4
【点拨】本题考查圆周角定理，熟练掌握同弧所对的圆周角是圆心角的一半，是解题的关键．
16．35
【分析】根据直径所对的圆周角是直角，可得∠BAC=55°，再根据切线的性质可得∠BAD=90°，即可求解．
解：∵AB为直径，
∴∠C=90°，
∵，
∴∠BAC=55°，
∵AD与相切，
∴AB⊥AD，即∠BAD=90°，
∴∠CAD=90°-∠BAC=35°．
故答案为：35
【点拨】本题主要考查了切线的性质，圆周角定理，熟练掌握切线的性质，直径所对的圆周角是直角是解题的关键．
17．9+9
【分析】首先过C作CM⊥AB于M，由弦AB已确定，可得要使△ABC的面积最大，只要CM取最大值即可，即可得当CM过圆心O时，CM最大，然后由圆周角定理，证得△AOB是等腰直角三角形，则可求得CM的长，继而求得答案．
解：作△ABC的外接圆⊙O，过C作CM⊥AB于M，

∵弦AB已确定，
∴要使△ABC的面积最大，只要CM取最大值即可，
如图所示，当CM过圆心O时，CM最大，
∵CM⊥AB，CM过O，
∴AM＝BM（垂径定理），
∴AC＝BC，
∵∠AOB＝2∠ACB＝2×45°＝90°，
∴OM＝AM＝AB＝×6＝3，
∴OA＝，
∴CM＝OC＋OM＝＋3，
∴S△ABC＝AB•CM＝×6×（＋3）＝9+9．
故答案为：9+9．
【点拨】此题考查了圆周角定理以及等腰直角三角形性质．注意得到当CM过圆心O时，CM最大是关键．
18．
【分析】根据折叠的性质得出是等边三角形，则，，根据阴影部分面积即可求解．
解：如图所示，连接，设交于点    
  
∵将沿弦翻折，使点与圆心重合，
∴，
又
∴，
∴是等边三角形，
∴，，
∴,
∴阴影部分面积
故答案为：．
19．（1）见分析（2）
【分析】（1）由AB为⊙O的直径，易证得AC⊥BD，又由DC=CB，根据线段垂直平分线的性质，可证得AD=AB，即可得：∠B=∠D；
（2）首先设BC=x，则AC=x-2，由在Rt△ABC中，，可得方程：，解此方程即可求得CB的长，继而求得CE的长．
解：（1）证明：∵AB为⊙O的直径，
∴∠ACB=90°
∴AC⊥BC
∵DC=CB
∴AD=AB
∴∠B=∠D
（2）设BC=x，则AC=x－2，
在Rt△ABC中，，
∴，解得：（舍去）．
∵∠B=∠E，∠B=∠D，
∴∠D=∠E
∴CD=CE
∵CD=CB，
∴CE=CB=．
20．（1）米；（2）不需要采取紧急措施，理由见分析
【分析】（1）连接，利用表示出的长，在中根据勾股定理求出的值即可；
（2）连接，在中，由勾股定理得出的长，进而可得出的长，据此可得出结论．
解：（1）连接，
由题意得：，
在中，由勾股定理得：，
解得，；
（2）连接，

，
在中，由勾股定理得：，
即：，
解得：．
．
，
不需要采取紧急措施．
【点拨】本题考查的是垂径定理的应用，根据题意作出辅助线，构造出直角三角形，利用勾股定理求解是解答此题的关键．
21．（1）见分析；（2）直线与⊙O相切，理由见分析．
【分析】（1）AB为⊙O的直径得，结合AB=AC，用HL证明全等三角形；
（2）由得BD=BC，结合AO=BO得OD为的中位线，由得，可得直线DE为⊙O切线．
解：（1）∵AB为⊙O的直径
∴
在和中

∴（HL）
（2）直线与⊙O相切，理由如下：
连接OD，如图所示：

由知：，
又∵OA=OB
∴OD为的中位线
∴
∵
∴
∵OD为⊙O的半径
∴DE与⊙O相切．
【点拨】本题考查了全等三角形的证明，切线的判定，熟知以上知识的应用是解题的关键．
22．（1）证明见分析；（2）.
【分析】（1）欲证明AC∥DE，只要证明AC⊥OD，ED⊥OD即可．
（2）作DM⊥OA于M，连接CD，CO，AD，首先证明四边形ACDE是平行四边形，根据S平行四边形ACDE=AE•DM，只要求出DM即可．
解：（1）∵ED与⊙O相切于D，
∴OD⊥DE，
∵F为弦AC中点，
∴OD⊥AC，
∴AC∥DE．
（2）作DM⊥OA于M，连接CD，CO，AD．
∵AC∥DE，AE=AO，
∴OF=DF，
∵AF⊥DO，
∴AD=AO，
∴AD=AO=OD，
∴△ADO是等边三角形，同理△CDO也是等边三角形，
∴∠CDO=∠DOA=60°，AE=CD=AD=AO=DD=a，
∴AO∥CD，又AE=CD，
∴四边形ACDE是平行四边形，易知DM=，
∴平行四边形ACDE面积=．

【点拨】本题考查切线的性质．熟练掌握切线的性质和两直线平行的判定是解决问题的关键.
23．（Ⅰ），； （Ⅱ）.
【分析】（Ⅰ）根据直角三角形的性质求出的大小，利用圆周角定理求出的大小；
（Ⅱ）首先根据直径所对的圆周角是90°，得出，然后根据圆内接四边形的性质得出，即可得出.
解：（Ⅰ）连接，如图所示，

∵是的切线，
∴.
∴.
∵，
∴，
∴.
∴.
∴；
（Ⅱ）连接，如图所示：

∵是的直径，
∴.
∴.
∵，
∴.
∵四边形是的内接四边形，
∴.
∵，
∴，
∴.
【点拨】此题属于容易题，主要考查切线的性质与判定、圆周角定理及其圆内接四边形的性质.失分原因：（1）不能根据直角三角形的性质求出的大小，不能利用圆周角定理求出的大小；（2）未掌握直径所对的圆周角是90°，不能灵活运用圆内接四边形的性质.
24．（1）四边形为正方形，理由见分析；（2）劣弧的长为；（3）
【分析】（1）根据切线的性质得到，根据正方形的判定定理即可得到结论；
（2）求得圆心角，利用弧长公式即可求解；
（3）过点作于点，在中，得到，，再设，据此求解即可．
（1）解：四边形为正方形．
理由：∵，分别与相切，
∴，，
∴，
又∵，
∴四边形为矩形，
∵，
∴四边形为正方形；
（2）解：由（1）可知，四边形为正方形，
∴，
∴劣弧的长；
（3）解：如图，过点作于点，
  
由（1）可知，四边形为正方形，
∴，，
∴，
在中，，
∴，，
设，则，．
∵，
∴，
解得，
∴．
【点拨】本题是圆的综合题，考查了正方形的判定，切线的性质，直角三角形的性质，弧长公式，正确的作出辅助线是解题的关键．