
- 专题2.45 圆中的动点问题(分层练习)(提升练)-2023-2024学年九年级数学上册基础知识专项突破讲与练(苏科版) 试卷 0 次下载
- 专题2.46 圆中的动点问题(分层练习)(培优练)-2023-2024学年九年级数学上册基础知识专项突破讲与练(苏科版) 试卷 1 次下载
- 专题2.48 圆中的折叠问题(培优练)-2023-2024学年九年级数学上册基础知识专项突破讲与练(苏科版) 试卷 0 次下载
- 专题2.49 圆(全章知识梳理与考点分类讲解)-2023-2024学年九年级数学上册基础知识专项突破讲与练(苏科版) 试卷 1 次下载
- 专题2.50 圆(全章分层练习)(基础练)-2023-2024学年九年级数学上册基础知识专项突破讲与练(苏科版) 试卷 0 次下载
苏科版九年级上册第2章 对称图形——圆2.1 圆精品课后复习题
展开专题2.47 圆中的折叠问题(基础练)
一、单选题
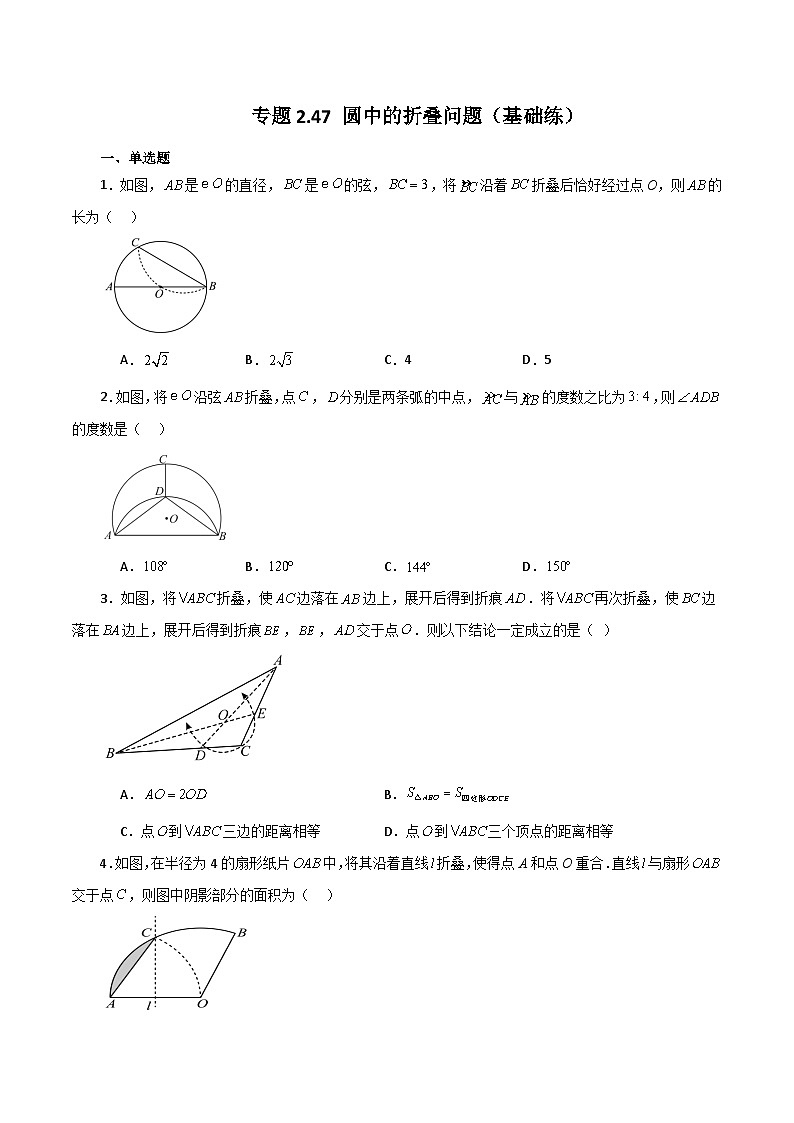
1.如图,是的直径,是的弦,,将沿着折叠后恰好经过点O,则的长为( )
A. B. C.4 D.5
2.如图,将沿弦折叠,点,分别是两条弧的中点,与的度数之比为,则的度数是( )
A. B. C. D.
3.如图,将折叠,使边落在边上,展开后得到折痕.将再次折叠,使边落在边上,展开后得到折痕,,交于点.则以下结论一定成立的是( )
A. B.
C.点到三边的距离相等 D.点到三个顶点的距离相等
4.如图,在半径为4的扇形纸片中,将其沿着直线折叠,使得点A和点O重合.直线与扇形交于点,则图中阴影部分的面积为( )
A. B. C. D.
5.如图,扇形纸片的半径为,沿所在直线折叠扇形纸片,圆心恰好落在上的点处,则阴影部分的面积是( )
A. B. C. D.
6.如图,在扇形中,,将扇形沿着过点B的直线折叠,点O恰好落在弧上的点D处,折痕交于点C,则弧的长为(结果保留)( )
A. B. C. D.
7.如图,将半径为的圆形纸片折叠后,圆弧恰好经过圆心,则圆弧的长为( )
A. B. C. D.
8.如图,将扇形OAB沿弦BC向下折叠,∠AOB=150°,OA=2,则图中阴影部分的周长为( )
A.+4 B.+4 C.+2 D.+2
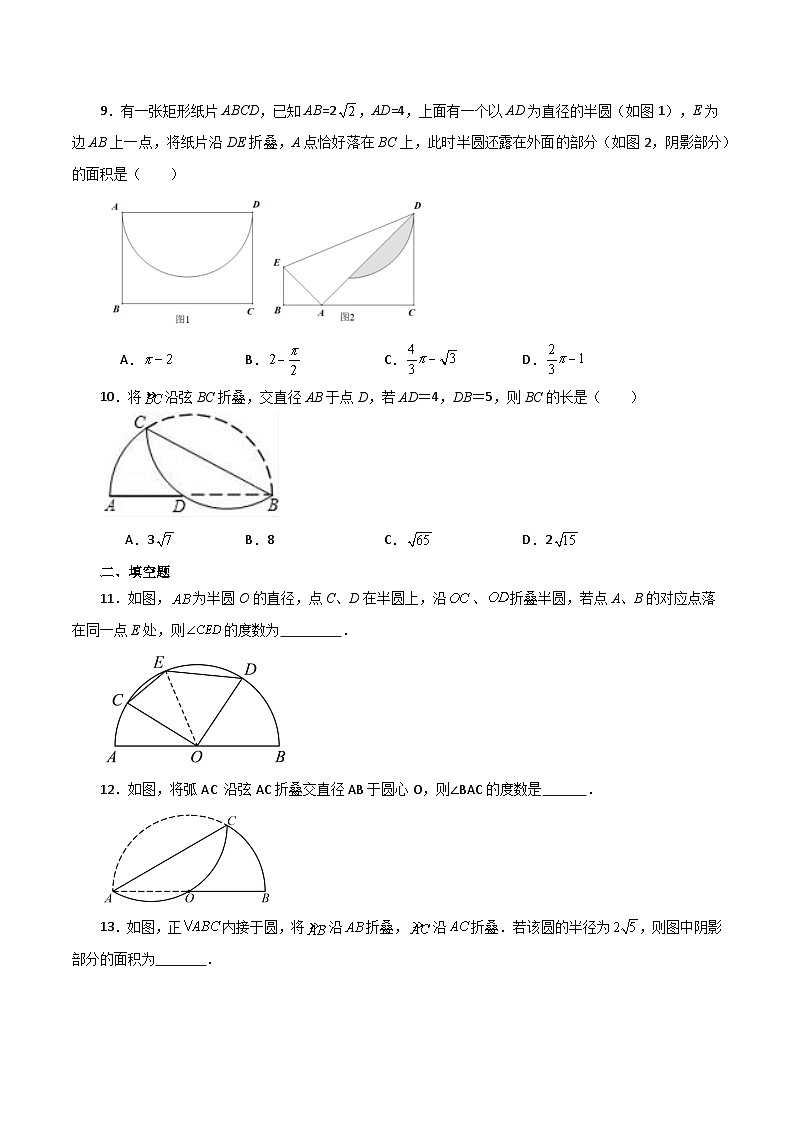
9.有一张矩形纸片ABCD,已知AB=2,AD=4,上面有一个以AD为直径的半圆(如图1),E为边AB上一点,将纸片沿DE折叠,A点恰好落在BC上,此时半圆还露在外面的部分(如图2,阴影部分)的面积是( )
A. B. C. D.
10.将沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是( )
A.3 B.8 C. D.2
二、填空题
11.如图,为半圆O的直径,点C、D在半圆上,沿、折叠半圆,若点A、B的对应点落在同一点E处,则的度数为 .
12.如图,将弧AC 沿弦AC折叠交直径AB于圆心O,则∠BAC的度数是 .
13.如图,正内接于圆,将沿折叠,沿折叠.若该圆的半径为,则图中阴影部分的面积为 .
14.如图,点C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在上的点D处,且l:l=1:3(l表示的长),若将此扇形OAB围成一个圆锥,则圆锥的底面半径与母线长的比为
15.如图,扇形纸片的半径为6,沿折叠扇形纸片,点恰好落在上的点处,图中阴影部分的面积为 .
16.如图,一个扇形零件的圆心角为,半径为2,将这个扇形零件折叠,使点A与点O恰好重合,折痕为,图中阴影为重合部分,则阴影部分的周长为 .
17.如图,以AB为直径的半圆沿弦BC折叠后,AB与弧CB相交于点D,若弧CD=弧BD,则∠B= .
18.如图,在矩形ABCD中,AB=4,BC=6,点E是BC的中点,点F在AD上运动,沿直线EF折叠四边形CDFE,得到四边形GHFE,其中点C落在点G处,连接AG,AH,则AG的最小值是 .
19.如图是一个以AB为直径的半⊙O,以OC,OD折叠半圆使得点A与点B落在同一点E,则∠CED= .
20.如图,在扇形OAB中,∠AOB=105°,OA=4,将扇形OAB沿着过点B的直线折叠,点O恰好落在弧的点D处,折痕BC交OA于点C,则阴影部分的面积为 .
21.如图,长方形ABCD中,,BC=2,点E是DC边上的动点,现将△BEC沿直线BE折叠,使点C落在点F处,则点D到点F的最短距离为 .
22.如图,在扇形OAB中,∠AOB=100°,半径OA=6,将扇形OAB沿过点A的直线折叠,点O恰好落在弧AB上的点D处,折痕交OB于点C,则弧BD的长为 .
三、解答题
23.如图,将半径为4cm的圆形纸片折叠后,弧AB恰好经过圆心O,求折痕弧AB的长.
24.中国扇文化有着深厚的文化底蕴,是民族文化的一个组成部分,它与竹文化、佛教文化有着密切关系.历来中国被誉为制扇王国.扇子主要材料是:竹、木、纸、象牙、玳瑁、翡翠、飞禽翎毛、其它棕榈叶、槟榔叶、麦秆、蒲草等也能编制成各种千姿百态的日用工艺扇,造型优美,构造精制,经能工巧匠精心镂、雕、烫、钻或名人挥毫题诗作画,使扇子艺术身价倍增.折扇,古称“聚头扇“,或称为撒扇,或折叠扇,以其收拢时能够二头合并归一而得名.如图,折扇的骨柄OA的长为5a,扇面的宽CA的长为3a,折扇张开的角度为n°,求出扇面的面积(用代数式表示).
25.综合与实践
在综合与实践活动课上,老师让同学们以“三角形纸片的折叠、旋转”为主题开展数学活动,探究线段长度的有关问题. 动手操作:
第一步:在图1中,测得三角形纸片ABC中,∠ACB=60°,BC
(1)BD____DE(请正确选择“>”、“=”、“<”中的一个);
(2)试判断△BCE 的形状,并给予证明;
(3)若BC=6,则△BCE 的外接圆的半径为_____.
参考答案
1.B
【分析】如图所示,过点O作于E,交于D,连接,由垂径定理得到,再根据折叠的性质得到,由此在中,由勾股定理求出的长即可得到答案.
解:如图所示,过点O作于E,交于D,连接,
∴,
∵,将沿着折叠后恰好经过点O,
∴,
在中,由勾股定理得: ,
∴,
∴,
∵是直径,
∴,
故选B.
【点拨】本题主要考查了垂径定理,勾股定理,折叠的性质,正确作出辅助线构造直角三角形是解题的关键.
2.A
【分析】根据与的度数之比为,点C,D分别是两条弧的中点,可知的度数,进一步可知优弧的度数,根据圆周角定理可得的度数.
解:∵与的度数之比为,点C,D分别是两条弧的中点,
∴的度数为,
根据折叠,优弧的度数为,
∴,
故选:A.
【点拨】本题考查了翻折变换(折叠问题),圆周角定理,熟练掌握折叠的性质是解题的关键.
3.C
【分析】根据是折痕,可知平分,平分,点为的内接圆的圆心,由此即可求解.
解:∵是折痕,
∴平分,平分,点为的内接圆的圆心,如图所示,
于,于,于,
选项, 的度数无法确定,与的数量关系也不确定,故选项不符合题意;
选项, 的长度不确定,的数量关系也不确定,故选项不符合题意;
选项,根据角平分的性质可得,,即点到三边的距离相等,故选项符合题意;
选项, ,故选项不符合题意;
故选:.
【点拨】本题主要考查三角形与圆的知识的综合,理解并掌握角平分线的性质,内切圆的知识是解题的关键.
4.A
【分析】连接,设直线l交于点D,根据折叠的性质可得,,从而得到是等边三角形,再由阴影部分的面积为,即可求解.
解:如图,连接,设直线l交于点D,
根据题意得:,,
∴是等边三角形,
∴,,
∴,
∴阴影部分的面积为.
故选:A.
【点拨】本题主要考查了求扇形的面积,等边三角形的判定和性质,熟练掌握扇形的面积公式是解题的关键.
5.A
【分析】连接,交于点,证明四边形是菱形,可得是等边三角形,,进而根据扇形面积减去菱形的面积即可求解.
解:如图所示,连接,交于点,
依题意,
∴四边形是菱形,
又
∴是等边三角形,
∴
∴
∴阴影部分面积
,
故选:A.
【点拨】本题考查了折叠的性质,求扇形面积,菱形的性质与判定,根据题意得出是等边三角形,是解题的关键.
6.B
【分析】如图,连接OD.根据折叠的性质、圆的性质推知△ODB是等边三角形,则易求∠AOD=100°-∠DOB=40°;然后由弧长公式弧长的公式 来求的长即可.
解:如图,连接OD.
根据折叠的性质知,OB=DB.
又∵OD=OB,
∴OD=OB=DB,即△ODB是等边三角形,
∴∠DOB=60°.
∵∠AOB=100°,
∴∠AOD=∠AOB-∠DOB=40°,
∴的长为 =2π.
故选:B.
【点拨】本题考查了弧长的计算,翻折变换(折叠问题).折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.所以由折叠的性质推知△ODB是等边三角形是解答此题的关键之处.
7.C
【分析】连接OA,OB,过点O作OD⊥AB,根据折叠得到OD=1,由OA=2,再得出∠AOD的度数,进而得出的长.
解:如图:连接OA,OB,过点O作OD⊥AB,
∵OA=2,
是翻折后得到的,且恰好经过圆心O,
∴OD=1,
在Rt△OAD中,
∵OA=2,OD=1,
∴cos∠AOD=,
∴∠AOD=60°,
∴∠AOB=120°,
∴=,
故选:C.
【点拨】本题主要考查了垂径定理以及翻折的性质以及勾股定理等知识,根据已知得出∠AOD=60°是解题关键.
8.A
【分析】根据题意知:阴影部分的周长是扇形的弧长与线段的长度之和,所以根据弧长的计算公式计算出弧长即可.
解:∵将扇形OAB沿弦BC向下折叠,∠AOB=150°,OA=2,
∴图中阴影部分的周长=+2×2=+4,
故选:A.
【点拨】本题考查了弧长的计算,折叠的性质,正确的识别图形是解题的关键.
9.A
【分析】根据折叠和直角三角形的边角关系可求出∠DAC=45°,进而求出阴影部分所在的圆心角的度数为90°,根据S阴影部分=S扇形DOF-S△ODF进行计算即可.
解:设阴影部分所在的圆心为O,AD与半圆弧交于点F,如图,连接OF,
由折叠的性质知:AD=BC=4,CD=2,
∴AC=2= CD,
∴△ADC是等腰直角三角形,
∴∠DAC=45°,
∵OD∥BC,
∴∠ODF=45°,
∴OD=OF=2,
∴∠ODF=∠OFD=45°,
∴∠DOF=180°-45°-45°=90°,
∴S阴影部分=S扇形DOF-S△ODF
=π-2.
故选:A.
【点拨】本题考查了折叠的性质,勾股定理,扇形、三角形面积计算,掌握扇形和三角形面积计算方法是正确计算的前提,求出相应的圆心角度数和半径是正确计算的关键.
10.A
【分析】若连接CD、AC,则根据同圆或等圆中,相等的圆周角所对的弦相等,求得AC=CD;过C作AB的垂线,设垂足为E,则DE= AD,由此可求出BE的长,进而可在Rt△ABC中,根据射影定理求出BC的长.
解:
连接CA、CD,
根据折叠的性质,知弧CD所对的圆周角等于∠CBD,
又∵弧AC所对的圆周角是∠CBA,
∵∠CBD=∠CBA,
∴AC=CD(相等的圆周角所对的弦相等) ,
∴△CAD是等腰三角形,
过C作CE⊥AB于E.
∵AD=4,则AE=DE=2,
∴BE=BD+DE=7,
在Rt△ACB中,CE⊥AB,根据射影定理,得:
=BE⋅AB=7×9=63,
故BC=.
故选:A.
【点拨】此题考查的是折叠的性质、圆周角定理、以及射影定理;能够根据圆周角定理来判断出△ACD是等腰三角形,是解答此题的关键
11./度
【分析】根据折叠的性质得到,再根据平角的定义得到,再根据等边对等角和三角形内角和定理求出,,再根据进行求解即可.
解:由折叠的性质可知,
∵,
∴,
∵,
∴, ,
∴
,
故答案为:.
【点拨】本题主要考查了圆的基本性质,等边对等角,折叠的性质,三角形内角和定理等等,灵活运用所学知识是解题的关键.
12.30°
【分析】过点O作OD⊥AC交AC于点D,延长OD交弧AC于点E,由折叠的性质及圆的基本性质可得OA=OE=2OD,进而问题得解.
解:过点O作OD⊥AC交AC于点D,延长OD交弧AC于点E,如图所示:
由将弧AC 沿弦AC折叠交直径AB于圆心O,可得OA=OE=2OD,
∠CAB=30°;
故答案为30°.
【点拨】本题主要考查圆的基本性质及含30°角的直角三角形,熟练掌握30°角的直角三角形的性质及圆的基本性质是解题的关键.
13.
【分析】根据题意得出和折叠后交于外接圆圆心O,从而得到阴影部分面积为△BOC的面积,根据圆的半径和圆心角的度数计算出△BOC的面积即可.
解:∵△ABC为正三角形,
∴和折叠后交于外接圆圆心O,
∴阴影部分面积为△BOC的面积,
过O作OD⊥BC,垂足为D,
∵∠BOC=120°,
∴∠OBC=∠OCB=30°,
∴OD=OB=,
∴BD==,
∴BC=2BD=2,
∴S阴影==,
故答案为:.
【点拨】本题考查了等边三角形的性质,三角形外接圆的性质,勾股定理等知识,解题的关键是根据题意将不规则部分进行合理转化.
14.2:9
【分析】连接OD,能得∠AOB的度数,再利用弧长公式和圆的周长公式可求解.
解:连接OD交OC于M.
由折叠的知识可得:OM=OA,∠OMA=90°,
∴∠OAM=30°,
∴∠AOM=60°,
∵且l:l=1:3,
∴∠AOB=80°
设圆锥的底面半径为r,母线长为l,
=2πr,
∴r:i=2:9.
故答案是2:9.
【点拨】本题运用了弧长公式和轴对称的性质,关键是运用了转化的数学思想.
15.
【分析】根据折叠的想找得到,,推出四边形是菱形,连接交于,根据等边三角形的性质得到,求得,根据菱形和扇形的面积公式即可得到结论.
解:沿折叠扇形纸片,点恰好落在上的点处,
,,
,
四边形是菱形,
连接交于,
,
是等边三角形,
,
,
,
,,
,
图中阴影部分的面积,
故答案为:.
【点拨】本题考查了扇形面积的计算,菱形的判定和性质,等边三角形的判定和性质,正确地作出辅助线是解题的关键.
16.
【分析】连接,利用折叠性质得由弧、线段和所围成的图形的周长等于阴影部分的周长,根据勾股定理求出 ,从而得到,然后根据扇形周长公式,进行计算即可.
解:连接,
在中,,
∴,
∴,
∴弧的长,
∴阴影部分的周长为弧的长.
【点拨】本题考查的是扇形周长的计算折叠的性质,将不规则图形周长转化为规则图形的周长、记住扇形周长的计算公式是解题的关键.
17./15度
【分析】如图,连接OC,首先证明,得出,根据圆周角定理即可求解.
解:如图,连接OC,
∵,,
,
∴,
∴,
∴,
故答案为:.
【点拨】本题考查了圆周角定理,翻折变换等知识,正确的作出辅助线是解题的关键.
18.2
【分析】如图,当A、G、E共线时,AG最小,先求出AE,根据AG=AE﹣EG即可解决问题.
解:如图,依题意:点G在以点E为圆心,长为半径的圆上运动,当A、G、E共线时,AG最小,
∵四边形ABCD是矩形,
∴∠B=90°,BE=EC=3,AB=4,
∴AE===5.
此时AG=AE﹣EG=5﹣3=2.
故答案为2.
【点拨】本题考查了矩形的性质,勾股定理,点到圆的距离,明确点和圆的位置关系是解决本题的关键.
19.135°
【分析】由以OC,OD折叠半圆使得点A与点B落在同一点E,可求∠COD=90°,△COE和△DOE是等腰三角形,根据三角形内角和定理可求.
解:∵以OC,OD折叠半圆使得点A与点B落在同一点E,
∴∠BOD=∠EOD=∠BOE,∠AOC=∠COE=∠AOE,
∴∠COD=∠COE+∠DOE=(∠BOE+∠AOE)=
∵OC=OD=OE
∴∠OCE=∠OEC,∠ODE=∠OED
∴∠CED=∠CEO+∠DEO
=
=
=
=
=135°
故答案为:135°.
【点拨】本题考查了折叠的性质,等腰三角形的性质,三角形内角和定理,熟练掌握这些性质定理是解题的关键.
20.2π-4/-4+2π
【分析】连接OD,交BC于E,根据对折得出BC⊥OD,DE=OE=2,∠DBE=∠OBE,OB=BD=4,求出△DOB是等边三角形,根据等边三角形的性质得出∠DOB=∠DBO=60°,求出∠COD=∠AOB-∠DOB=45°,求出CE=OE=2,再分别求出扇形AOD和△COD的面积即可.
解:连接OD,交BC于E,
∵延BC对折O和D重合,OD=4,
∴BC⊥OD,DE=OE=2,∠DBE=∠OBE,OB=BD=4,
∴∠BEO=90°,△DOB是等边三角形,
∴∠DOB=∠DBO=60°,
∵∠AOB=105°,
∴∠COD=∠AOB-∠DOB=45°,
∵∠OEC=90°,
∴CE=OE=2,
∴阴影部分的面积
=S扇形AOD-S△COD
=2π-4,
故答案为:2π-4.
【点拨】本题考查了等边三角形的性质和判定,直角三角形的性质,扇形的面积计算等知识点,能把求不规则图形的面积转化成求规则图形的面积是解此题的关键,注意:圆心角为n°,半径为r的扇形的面积为.
21.2
【分析】由题意易得点F的运动轨迹是以点B为圆心,BC长为半径的圆弧,连接BD,然后根据隐圆问题可进行求解.
解:由题意得:点F的运动轨迹是以点B为圆心,BC长为半径的圆弧,
连接BD,交圆弧于点H,如图所示:
∴当点F与点H重合时,点D到点F的距离为最短,
∵四边形ABCD是矩形,,BC=2,
∴,
∴,
∴,即点D到点F的最短距离为2;
故答案为2.
【点拨】本题主要考查隐圆问题,矩形与折叠,勾股定理,解题的关键是分析得出点F的运动轨迹.
22.π.
【分析】根据折叠的性质可得:AO=AD,从而证出△AOD为等边三角形,即可求出∠AOD=60°,从而求出∠BOD,最后根据弧长公式计算即可.
解:连接AD,如图,
∵扇形OAB沿过点A的直线折叠,点O恰好落在弧AB上的点D处,折痕交OB于点C,
∴AC垂直平分OD,
∴AO=AD,
而AO=OD,
∴OA=OD=AD,
∴△AOD为等边三角形,
∴∠AOD=60°,
∴∠BOD=∠AOB﹣∠AOD=100°﹣60°=40°,
∴弧BD的长==π.
故答案为π.
【点拨】此题考查的是折叠的性质、等边三角形的判定及性质和求弧长,掌握折叠的性质、等边三角形的定义、等边三角形的每个内角都是60°和弧长公式是解决此题的关键.
23.
【分析】连接OA,OB,过点O作OD⊥AB,根据折叠得到OD=2,由OA=4,再得出∠AOD的度数,进而得出的长.
解:如图:连接OA,OB,过点O作OD⊥AB,
∵OA=4,
是翻折后得到的,且恰好经过圆心O,
∴OD=2,
在Rt△OAD中,
∵OA=4,OD=2,
∴∠OAD=30°
∴∠AOD=60°,
∴∠AOB=120°,
∴的长为==.
【点拨】此题主要考查了垂径定理以及翻折的性质以及勾股定理、求弧长等知识,根据已知得出∠AOD=60°是解题关键.
24.
【分析】由OA=5a、AC=3a得OC=2a,根据扇面的面积S=﹣列式化简即可得.
解:∵OA=5a,AC=3a,
∴OC=2a
∴扇面的面积S=﹣=﹣===.
【点拨】本题考查了扇形的面积计算,掌握扇形面积的计算公式和扇面面积=大扇形面积﹣小扇形面积是解题的关键.
25.(1)=;(2)是等边三角形,证明见分析;(3).
【分析】(1)根据折叠的性质可直接得出结果;
(2)由折叠可得,再由题中,可证明是等边三角形;
(3)由(2)得是等边三角形,作出其外接圆,圆心为O,连接BO,过点O作,根据外接圆圆心为三条线段中垂线的交点及等边三角形三线合一的性质可得:,,在直角三角形中利用角的特殊性质及勾股定理求解即可.
解:(1)根据折叠的性质可得:,
故答案为:=;
(2)是等边三角形,
∵由折叠可得,
∴,
∵,
∴是等边三角形;
(3)如图所示,由(2)得是等边三角形,作出其外接圆,圆心为O,连接BO,过点O作,
∵是等边三角形,
∴,,
∴,
,
即,
∴,
故答案为:.
【点拨】题目主要考查折叠的性质,等边三角形的判定与性质,三角形外接圆的性质,勾股定理解三角形等,理解题意,作出相应图形,综合运用这些知识点是解题关键.
专题2.55 圆(全章直通中考)(培优练)-2023-2024学年九年级数学上册基础知识专项突破讲与练(苏科版): 这是一份专题2.55 圆(全章直通中考)(培优练)-2023-2024学年九年级数学上册基础知识专项突破讲与练(苏科版),共37页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
专题2.54 圆(全章直通中考)(提升练)-2023-2024学年九年级数学上册基础知识专项突破讲与练(苏科版): 这是一份专题2.54 圆(全章直通中考)(提升练)-2023-2024学年九年级数学上册基础知识专项突破讲与练(苏科版),共29页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
专题2.53 圆(全章直通中考)(基础练)-2023-2024学年九年级数学上册基础知识专项突破讲与练(苏科版): 这是一份专题2.53 圆(全章直通中考)(基础练)-2023-2024学年九年级数学上册基础知识专项突破讲与练(苏科版),共29页。













