专题2.29 切线长定理（直通中考）-2023-2024学年九年级数学上册基础知识专项突破讲与练（苏科版）

这是一份专题2.29 切线长定理（直通中考）-2023-2024学年九年级数学上册基础知识专项突破讲与练（苏科版），共34页。

专题2.29 切线长定理（直通中考）
【要点回顾】
1．切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.
2．圆外切四边形的性质：圆外切四边形的两组对边之和相等.
3．三角形的内心：三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心.
一、单选题
1．（2023·山东·统考中考真题）在中，，下列说法错误的是（　　）
A． B．
C．内切圆的半径 D．当时，是直角三角形
2．（2023·湖南永州·统考中考真题）如图，在中，，以为圆心，任意长为半径画弧，分别交，于点，，再分别以，为圆心，大于的定长为半径画弧，两弧交于点，作射线交于点，作，垂足为，则下列结论不正确的是（     ）
  
A． B．
C． D．一定经过的内心
3．（2023·山东聊城·统考中考真题）如图，点O是外接圆的圆心，点I是的内心，连接，．若，则的度数为（     ）
  
A． B． C． D．
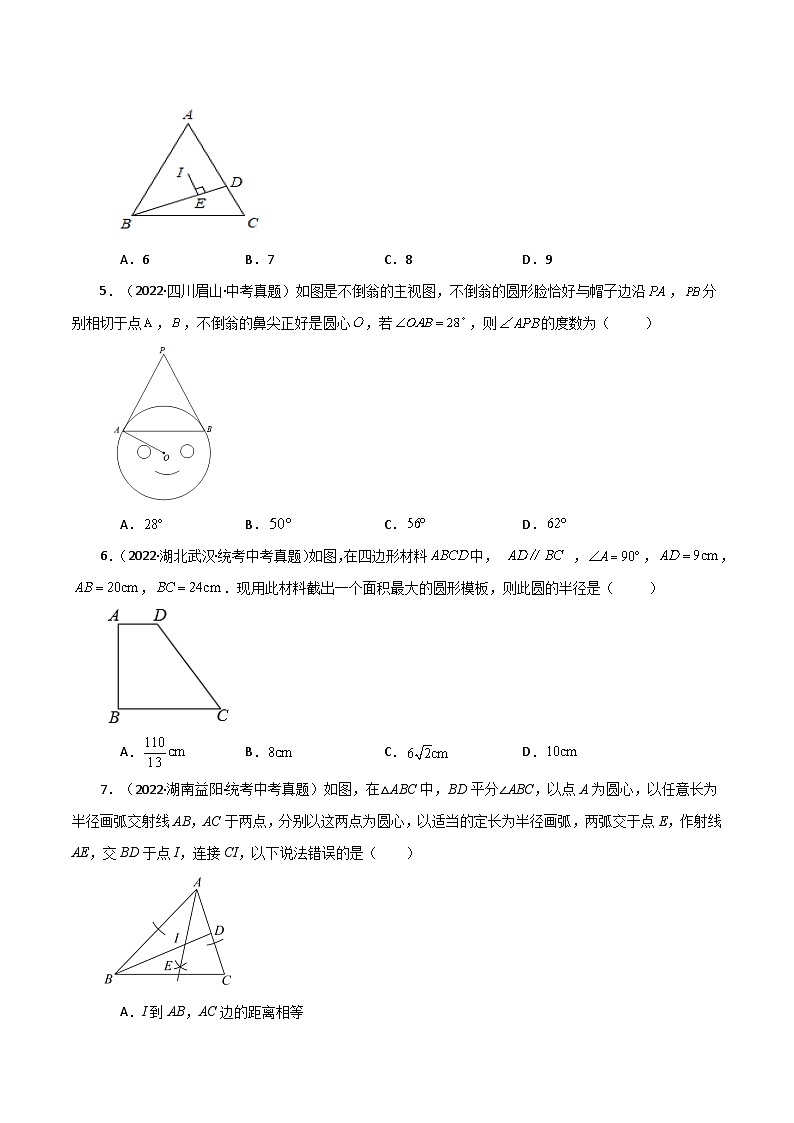
4．（2022·山东淄博·统考中考真题）如图，在△ABC中，AB＝AC，点D在AC边上，过△ABD的内心I作IE⊥BD于点E．若BD＝10，CD＝4，则BE的长为（     ）

A．6 B．7 C．8 D．9
5．（2022·四川眉山·中考真题）如图是不倒翁的主视图，不倒翁的圆形脸恰好与帽子边沿，分别相切于点，，不倒翁的鼻尖正好是圆心，若，则的度数为（     ）

A． B． C． D．
6．（2022·湖北武汉·统考中考真题）如图，在四边形材料中， ，，，，．现用此材料截出一个面积最大的圆形模板，则此圆的半径是（     ）

A． B． C． D．
7．（2022·湖南益阳·统考中考真题）如图，在△ABC中，BD平分∠ABC，以点A为圆心，以任意长为半径画弧交射线AB，AC于两点，分别以这两点为圆心，以适当的定长为半径画弧，两弧交于点E，作射线AE，交BD于点I，连接CI，以下说法错误的是（　　）

A．I到AB，AC边的距离相等
B．CI平分∠ACB
C．I是△ABC的内心
D．I到A，B，C三点的距离相等
8．（2022·广西贵港·中考真题）下列命题为真命题的是（     ）
A． B．同位角相等
C．三角形的内心到三边的距离相等 D．正多边形都是中心对称图形
9．（2022·四川德阳·统考中考真题）如图，点是的内心，的延长线和的外接圆相交于点，与相交于点，则下列结论：①；②若，则；③若点为的中点，则；④．其中一定正确的个数是（     ）

A．1 B．2 C．3 D．4
10．（2022·贵州遵义·统考二模）如图，AB为的直径，延长AB到点P，过点P作的切线PC，PD，切点分别为C，D，连接CD交AP于点M，连接BD，AD．若，，则AD的长为（     ）

A． B． C．2 D．
二、填空题
11．（2023·湖北·统考中考真题）如图，在中，的内切圆与分别相切于点，，连接的延长线交于点，则 ．
  
12．（2022·四川宜宾·统考中考真题）我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形（如图所示）．若直角三角形的内切圆半径为3，小正方形的面积为49，则大正方形的面积为 ．

13．（2022·内蒙古·中考真题）如图，在等腰直角三角形中，，点P在以斜边为直径的半圆上，M为的中点，当点P沿半圆从点A运动至点B时，点M运动的路径长是 ．
  
14．（2022·辽宁锦州·统考二模）如图所示，AB、AC为⊙O的切线，B和C是切点，延长OB到D，使BD＝OB，连接AD．∠DAC＝78°，那么∠AOD等于 度．

15．（2022·浙江杭州·模拟预测）如图，直线，，分别与相切于，，，且，若，，则的长等于 ．

16．（2022·安徽蚌埠·统考二模）如图，中，，M是BC的中点，的内切圆与AB，BM分别相切于点D，E，连接DE．若，则的大小为 ．

17．（2022·浙江嘉兴·一模）如图，在中，点是直径的延长线上一点，过点作的切线，C为切点．连接，若，则的度数为 ．

18．（2022·湖南株洲·统考一模）已知点P（，）和直线，求点P到直线的距离d可用公式计算．根据以上材料解决下面问题：如图，⊙C的圆心C的坐标为（1，1），半径为1，直线AB的表达式为，P是直线AB上的动点，Q是⊙C上的动点，则PQ的最小值是 ．   

三、解答题
19．（2022·黑龙江绥化·统考中考真题）已知：．
（1）尺规作图：用直尺和圆规作出内切圆的圆心O；（只保留作图痕迹，不写作法和证明）
（2）如果的周长为14，内切圆的半径为1.3，求的面积．








20．（2023·湖北武汉·统考中考真题）如图，都是的半径，．
（1）求证：；
（2）若，求的半径．








21．（2022·内蒙古包头·中考真题）如图，为的切线，C为切点，D是上一点，过点D作，垂足为F，交于点E，连接并延长交于点G，连接，已知．
（1）若的半径为5，求的长；
（2）试探究与之间的数量关系，写出并证明你的结论．（请用两种证法解答）








22．（2022·天津·统考中考真题）已知为的直径，，C为上一点，连接．
（1）如图①，若C为的中点，求的大小和的长；
（2）如图②，若为的半径，且，垂足为E，过点D作的切线，与的延长线相交于点F，求的长．




23．（2022·江西·统考中考真题）（1）课本再现：在中，是所对的圆心角，是所对的圆周角，我们在数学课上探索两者之间的关系时，要根据圆心O与的位置关系进行分类．图1是其中一种情况，请你在图2和图3中画出其它两种情况的图形，并从三种位置关系中任选一种情况证明；
（2）知识应用：如图4，若的半径为2，分别与相切于点A，B，，求的长．
















24．（2023·吉林长春·统考中考真题）【感知】如图①，点A、B、P均在上，，则锐角的大小为__________度．
                 
【探究】小明遇到这样一个问题：如图②，是等边三角形的外接圆，点P在上（点P不与点A、C重合），连结、、．求证：．小明发现，延长至点E，使，连结，通过证明，可推得是等边三角形，进而得证．
下面是小明的部分证明过程：
证明：延长至点E，使，连结，
四边形是的内接四边形，
．
，
．
是等边三角形．
，

请你补全余下的证明过程．
【应用】如图③，是的外接圆，，点P在上，且点P与点B在的两侧，连结、、．若，则的值为__________．











参考答案
1．C
【分析】根据三角形三边关系、三角形面积、内切圆半径的计算以及勾股定理逆定理逐一求解即可．
解：∵，
∴即，故A说法正确；
当时，，
若以为底，高，
∴，故B说法正确；
设内切圆的半径为r，
则，
∵，
∴，，
∵，
∴，
∴，故C说法错误；
当时，，
∴是直角三角形，故D说法正确；
故选：C．
【点拨】本题考查了三角形三边关系，三角形面积，三角形内切圆半径以及勾股定理的逆定理，掌握内切圆半径与圆的面积周长之间的关系是解题的关键．
2．C
【分析】根据作图可得是的角平分线，根据角平分线的性质得出，即可判断B，证明，根据全等三角形的性质，即可判断A，根据三角形内心的定义，即可判断D选项，假设成立，得出，即可判断C选项．
解：根据作图可得是的角平分线，点在上，，
∴，故B选项正确，
在中，
，
∴，
∴，故A选项正确；
∵是的角平分线，三角形的内心是三条角平分线的交点，
∴一定经过的内心，故D选项正确；
若，则，，
又，
则，
∴，而题目没有给出这个条件，故C选项不一定正确，
故选：C．
【点拨】本题考查了作角平分线，三角形角平分线的定义，全等三角形的性质与判定，三角形的内心的定义，熟练掌握基本作图是解题的关键．
3．C
【分析】根据三角形内心的定义可得的度数，然后由圆周角定理求出，再根据三角形内角和定理以及等腰三角形的性质得出答案．
解：连接，
∵点I是的内心，，
∴，
∴，
∵，
∴，
故选：C．
  
【点拨】本题主要考查了三角形内心的定义和圆周角定理，熟知三角形的内心是三角形三个内角平分线的交点是解题的关键．
4．B
【分析】过点作，根据切线长定理设，进而结合已知条件表示出，求得的长，进而即可求解．
解：如图，过点作，

∵是的内心，
∴，
设，
∵BD＝10，
∴，
∴,，
∵，
∴，
解得，
∴，
故选B．
【点拨】本题考查了三角形内心的性质，切线长定理，掌握切线长定理是解题的关键．
5．C
【分析】连OB，由AO=OB得，∠OAB=∠OBA=28°，∠AOB=180°-2∠OAB=124°；因为PA、PB分别相切于点A、B，则∠OAP=∠OBP=90°，利用四边形内角和即可求出∠APB．
解：连接OB，

∵OA=OB，
∴∠OAB=∠OBA=28°，
∴∠AOB=124°，
∵PA、PB切⊙O于A、B，
∴OA⊥PA，OP⊥AB，
∴∠OAP+∠OBP=180°，
∴∠APB+∠AOB=180°；
∴∠APB=56°．
故选：C
【点拨】本题考查切线的性质，三角形和四边形的内角和定理，切线长定理，等腰三角形的性质等知识，解题的关键是学会添加常用辅助线，构造等腰三角形解决问题．
6．B
【分析】如图所示，延长BA交CD延长线于E，当这个圆为△BCE的内切圆时，此圆的面积最大，据此求解即可．
解：如图所示，延长BA交CD延长线于E，当这个圆为△BCE的内切圆时，此圆的面积最大，
∵，∠BAD=90°，
∴△EAD∽△EBC，∠B=90°，
∴，即，
∴，
∴EB=32cm，
∴，
设这个圆的圆心为O，与EB，BC，EC分别相切于F，G，H，
∴OF=OG=OH，
∵，
∴，
∴，
∴，
∴此圆的半径为8cm，
故选B．

【点拨】本题主要考查了三角形内切圆半径与三角形三边的关系，勾股定理，正确作出辅助线是解题的关键．
7．D
【分析】根据作图先判断AE平分∠BAC，再由三角形内心的性质解答即可．
解：A.由作图可知，AE是∠BAC的平分线，
∴I到AB，AC边的距离相等，故选项正确，不符合题意；
B.∵BD平分∠ABC，三角形三条角平分线交于一点，
∴CI平分∠ACB，故选项正确，不符合题意；
C.由上可知，I是△ABC的内心，故选项正确，不符合题意，
D.∵I是△ABC的内心，
∴I到AB，AC，BC的距离相等，不是到A，B，C三点的距离相等，故选项错误，符合题意；
故选：D．
【点拨】此题考查尺规作图，涉及三角形内心的性质，解题的关键是掌握基本的尺规作图和三角形内心的性质．
8．C
【分析】根据判断命题真假的方法即可求解．
解：当时，，故A为假命题，故A选项错误；
当两直线平行时，同位角才相等，故B为假命题，故B选项错误；
三角形的内心为三角形内切圆的圆心，故到三边的距离相等，故C为真命题，故C选项正确；
正三角形不是中心对称图形，故D为假命题，故D选项错误，
故选：C．
【点拨】本题考查了真假命题的判断，熟练掌握其判断方法是解题的关键．
9．D
【分析】根据点是的内心，可得，故①正确；连接BE，CE，可得∠ABC+∠ACB =2（∠CBE+∠BCE），从而得到∠CBE+∠BCE=60°，进而得到∠BEC=120°，故②正确； ，得出，再由点为的中点，则成立，故③正确；根据点是的内心和三角形的外角的性质，可得，再由圆周角定理可得，从而得到∠DBE=∠BED，故④正确；即可求解．
解：∵点是的内心，
∴，故①正确；
如图，连接BE，CE，

∵点是的内心，
∴∠ABC=2∠CBE，∠ACB=2∠BCE，
∴∠ABC+∠ACB =2（∠CBE+∠BCE），
∵∠BAC=60°，
∴∠ABC+∠ACB=120°，
∴∠CBE+∠BCE=60°，
∴∠BEC=120°，故②正确；
∵点是的内心，
∴，
∴,
∵点为的中点，
∴线段AD经过圆心O，
∴成立，故③正确；
∵点是的内心，
∴，
∵∠BED=∠BAD+∠ABE，
∴，
∵∠CBD=∠CAD，
∴∠DBE=∠CBE+∠CBD=∠CBE+∠CAD，
∴，
∴∠DBE=∠BED，
∴，故④正确；
∴正确的有4个．
故选：D
【点拨】本题主要考查了三角形的内心问题，圆周角定理，三角形的内角和等知识，熟练掌握三角形的内心问题，圆周角定理，三角形的内角和等知识是解题的关键．
10．A
【分析】连接，设，的半径为，由勾股定理求出，在中，由可得方程，代入的值，可求出x的值，再根据勾股定理可得出结论．
解：连接，如图所示，

∵PC，PD是的切线，
∴
设
∵
∴
∴
设的半径为
∴
在中，，
解得，
在中，
∵是的切线，
∴
在中，
∵
∵
∴
整理得，
∴
解得，或（舍去）
∴
∴

在中，，故A正确．
故选：A．
【点拨】本题主要考查了切线长定理，垂径定理，勾股定理等知识，正确作出辅助线是解答本题的关键．
11．/度
【分析】如图所示，连接，设交于H，由内切圆的定义结合三角形内角和定理求出，再由切线长定理得到，进而推出是的垂直平分线，即，则．
解：如图所示，连接，设交于H，
∵是的内切圆，
∴分别是的角平分线，
∴，
∵，
∴，
∴，
∴，
∵与分别相切于点，，
∴，
又∵，
∴是的垂直平分线，
∴，即，
∴，
故答案为：．
  
【点拨】本题主要考查了三角形内切圆，切线长定理，三角形内角和定理，线段垂直平分线的判定，三角形外角的性质，正确作出辅助线是解题的关键．
12．289
【分析】设直角三角形的三边分别为，较长的直角边为较短的直角边为为斜边，由切线长定理可得，直角三角形的内切圆的半径等于，即，根据小正方的面积为49，可得，进而计算即即可求解．
解：设四个全等的直角三角形的三边分别为，较长的直角边为较短的直角边为为斜边，
直角三角形的内切圆半径为3，小正方形的面积为49，
，
①，②，
，
③，
，
解得或（舍去），
大正方形的面积为，
故答案为：．
【点拨】本题考查了切线长定理，勾股定理，解一元二次方程，二元一次方程组，掌握直角三角形的内切圆的半径等于是解题的关键．
13．
【分析】取的中点、的中点、的中点，连接、、、、、，可得四边形CEOF是正方形，由OP=OC得OM⊥PC，则可得点M的运动路径，从而求得路径的长．
解：取的中点、的中点、的中点，连接、、、、、，如图，
  
则，且，，，
∴四边形CEOF为平行四边形，
∵AC=BC，∠ACB=90°，
∴四边形为正方形，
∴CE=CF=，EF=OC，
由勾股定理得：，
∵在等腰中，，
∴，
∴，，
∵为的中点，
∴，
∴，  
∴点在以为直径的圆上，
当点点在点时，点在点；点点在点时，点在点，
∴点的路径为以为直径的半圆，
∴点运动的路径长．
故答案是：．
【点拨】本题考查了勾股定理、直角三角形斜边上中线的性质、三角形中位线定理、等腰三角形的性质及正方形的判定，确定点M的运动路径是关键与难点．
14．64
【分析】由已知条件推导出∠CAO=∠OAB=∠BAD，∠ABD=90°，由此根据∠DAC=78°，能求出∠AOD的大小．
解：∵AB、AC为⊙O的切线，B和C是切点，BD=OB，
垂直平分,∠CAO=∠OAB

∠OAB=∠BAD，
∴∠CAO=∠OAB=∠BAD，∠ABD=90°，
∵∠DAC=78°，
∴∠BAO=∠DAC=26°，
∴∠AOD=90°-26°=64°．
故答案为：64．
【点拨】本题考查角的大小的求法，解题时要认真审题，注意切线性质的灵活运用是解题的关键．
15．10cm
【分析】根据平行线的性质以及切线长定理，即可证明，再根据勾股定理即可求得的长，再结合切线长定理即可求解．
解： ，
，
、，分别与相切于、、，
，，，，
，
，
，
．
故答案为：10cm．
【点拨】此题主要是考查了切线长定理．从圆外一点引圆的两条切线，它们的切线长相等，且圆心和这点的连线平分两条切线的夹角．
16．30°/30度
【分析】利用直角三角形斜边上的中线的性质证明△ABM是等腰三角形，得到∠B＝∠BAM，的内切圆与AB，BM分别相切于点D，E，利用切线长定理证明△BDE是等腰三角形，得到∠BED＝∠BDE，利用得到∠BED＝∠BMA，∠BDE＝∠BAM，进一步证得△ABM是等边三角形，∠B＝60°，即可求出∠C的大小．
解：∵，
∴△ABC是直角三角形
∵M是BC的中点，
∴AM＝BM＝，
∴△ABM是等腰三角形，
∴∠B＝∠BAM，
∵的内切圆与AB，BM分别相切于点D，E，
∴BD＝BE，
∴△BDE是等腰三角形，
∴∠BED＝∠BDE，
∵，
∴∠BED＝∠BMA，∠BDE＝∠BAM，
∴∠BMA＝∠BAM
∴∠B＝∠BMA＝∠BAM，
∴△ABM是等边三角形，
∴∠B＝60°，
∴∠C＝90°－∠B＝30°，
故答案为：30°．
【点拨】此题考查了直角三角形的性质、圆的切线长定理、等腰三角形的判定和性质、等边三角形的判定和性质、平行线的性质等知识，熟练掌握相关性质定理是解题的关键．
17．
【分析】连接，根据切线的性质，得出，再根据直角三角形两锐角互余，得出的度数，然后再根据三角形的外角和定理，得出，再根据等边对等角，得出，再进行计算即可得出的度数．
解：连接，
∵是的切线，为切点，
∴，
∴，
在中，
∵，
∴，
∵点是直径的延长线上一点，
∴，
又∵，
∴，
∴，
∴，
即．

故答案为：
【点拨】本题考查了切线的性质、直角三角形两锐角互余、三角形的外角和定理、等边对等角，解本题的关键在熟练掌握相关的性质定理．
18．
【分析】连接，先根据点与圆的位置关系可得当点为与的交点时，取得最小值，再根据垂线段最短可知，当时，取得最小值，然后利用点到直线的距离公式可得的长，由此即可得．
解：的半径为1，
，
如图，连接，

则当点为与的交点时，取得最小值，最小值为，
由垂线段最短可知，当时，取得最小值，
直线的表达式为，的坐标为，
的最小值为，
则的最小值为，
故答案为：．
【点拨】本题考查了点与圆的位置关系、垂线段最短等知识点，正确找出取得最小值时，点的位置是解题关键．
19．（1）作图见详解；（2）9.1
【分析】（1）根据角平分线的性质可知角平分线的交点为三角形内切圆的圆心，故只要作出两个角的角平分线即可；
（2）利用割补法，连接OA，OB，OC，作OD⊥AB，OE⊥BC，OF⊥AC，这样将△ABC分成三个小三角形，这三个小三角形分别以△ABC的三边为底，高为内切圆的半径，利用提取公因式可将周长代入，进而求出三角形的面积．
（1）解：如下图所示，O为所求作点，

（2）解：如图所示，连接OA，OB，OC，作OD⊥AB，OE⊥BC，OF⊥AC，

∵内切圆的半径为1.3，
∴OD=OF=OE=1.3，
∵三角形ABC的周长为14，
∴AB+BC+AC=14，
则

故三角形ABC的面积为9.1．
【点拨】本题考查三角形的内切圆，角平分线的性质，割补法求几何图形的面积，能够将角平分线的性质与三角形的内切圆相结合是解决本题的关键．
20．（1）见分析；（2）
【分析】（1）由圆周角定理得出，，再根据，即可得出结论；
（2）过点作半径于点，根据垂径定理得出，证明，得出，在中根据勾股定理得出，在中，根据勾股定理得出，求出即可．
解：（1）证明：∵，
∴，
∵，
∴，
，
．
（2）解：过点作半径于点，则，
，
∴，
，
，
，
在中，
，
在中，，
，
，即的半径是．
  
【点拨】本题主要考查了勾股定理，垂径定理，圆周角定理，解题的关键是作出辅助线，熟练掌握圆周角定理．
21．（1）；（2），证明见分析
【分析】（1）由题意得，，根据得，根据切线的性质得，即，根据题意得，则，即可得，根据角之间的关系和边之间的关系得是等边三角形，即可得∴，则,根据题意得，，，在中，根据锐角三角形函数即可得；
（2）方法一：根据题意和边、角之间得关系得，为等边三角形，可得，在中，根据直角三角形的性质得，即；方法二：连接，过点O作，垂足为H，根据题意得，四边形是矩形，所以，根据等边三角形的性质得，根据边之间的关系得CE=OE，根据HL得，即可得，由此即可得．
（1）解：如图所示，连接．

∵，
∴，
∵，
∴，
∵为的切线，C为切点，
∴，
∴，
∵，垂足为F，
∴，
∴，
∴，
∴，
∴，
∴．
∵，
∴是等边三角形，
∴，
∴．
∵的半径为5，
∴，
∵是的直径，
∴，
∴在中，．
（2），证明如下
证明：方法一：如图所示，

∵，
∴，
∴．
∵，
∴为等边三角形，
∴．
∵，
∴．
∴在中，，
∴，
即；
方法二：如图所示，连接，过点O作，垂足为H，

∴，
∵，
∴四边形是矩形，
∴，    
∵是等边三角形，
∴，
∵，
∴，即DE=2EH，
∵，
∴，
∴，
∴，
在和中，

∴（HL），
∴，
∴．
【点拨】本题考查了圆的综合，平行线的判定与性质，锐角三角函数，等边三角形的判定与性质，矩形的判定与性质，全等三角形的判定与性质，解题的关键是掌握这些知识点．
22．（1），；（2）
【分析】（1）由圆周角定理得，由C为的中点，得，从而，即可求得的度数，通过勾股定理即可求得AC的长度；
（2）证明四边形为矩形，FD=CE= CB，由勾股定理求得BC的长，即可得出答案．
解：（1）∵为的直径，
∴，
由C为的中点，得，
∴，得，
在中，，
∴；
根据勾股定理，有，
又，得，
∴；
（2）∵是的切线，
∴，即，
∵，垂足为E，
∴，
同（1）可得，有，
∴，
∴四边形为矩形，
∴，于是，
在中，由，得，
∴．
【点拨】本题是圆的综合题，考查了圆周角定理，切线的性质，等腰直角三角形的性质，垂径定理，勾股定理和矩形的判定和性质等，解题的关键是利用数形结合的思想解答此题．
23．（1）见分析；（2）
【分析】（1）①如图2，当点O在∠ACB的内部，作直径，根据三角形外角的性质和等腰三角形的性质可得结论；②如图3，当O在∠ACB的外部时，作直径CD，同理可理结论；
（2）如图4，先根据（1）中的结论可得∠AOB=120°，由切线的性质可得∠OAP=∠OBP=90°，可得∠OPA=30°，从而得PA的长．
解：（1）①如图2，连接CO，并延长CO交⊙O于点D，

∵OA=OC=OB，
∴∠A=∠ACO，∠B=∠BCO，
∵∠AOD=∠A+∠ACO=2∠ACO，∠BOD=∠B+∠BCO=2∠BCO，
∴∠AOB=∠AOD+∠BOD=2∠ACO+2∠BCO=2∠ACB，
∴∠ACB=∠AOB；
如图3，连接CO，并延长CO交⊙O于点D，

∵OA=OC=OB，
∴∠A=∠ACO，∠B=∠BCO，
∵∠AOD=∠A+∠ACO=2∠ACO，∠BOD=∠B+∠BCO=2∠BCO，
∴∠AOB=∠AOD-∠BOD=2∠ACO-2∠BCO=2∠ACB，
∴∠ACB=∠AOB；
（2）如图4，连接OA，OB，OP，

∵∠C=60°，
∴∠AOB=2∠C=120°，
∵PA，PB分别与⊙O相切于点A，B，
∴∠OAP=∠OBP=90°，∠APO=∠BPO=∠APB=（180°-120°）=30°，
∵OA=2，
∴OP=2OA=4，
∴PA=
【点拨】本题考查了切线长定理，圆周角定理等知识，掌握证明圆周角定理的方法是解本题的关键．
24．感知：；探究：见分析；应用：．
【分析】感知：由圆周角定理即可求解；
探究：延长至点E，使，连结，通过证明，可推得是等边三角形，进而得证；
应用：延长至点E，使，连结，通过证明得，可推得是等腰直角三角形，结合与可得，代入即可求解．
解：感知：
由圆周角定理可得，
故答案为：；
探究：
证明：延长至点E，使，连结，
四边形是的内接四边形，
．
，
．
是等边三角形．
，
，
∴，，
，
是等边三角形，
，
，
即；
应用：
延长至点E，使，连结，
四边形是的内接四边形，
．
，
．
，
，
∴，，
，
是等腰直角三角形，
，
，
即，
，
，
，
，
，
，
故答案为：．

【点拨】本题考查了圆周角定理，圆内接四边形对角互补，邻补角，全等三角形的判定和性质，等边三角形、等腰直角三角形的判定和性质，勾股定理解直角三角形；解题的关键是做辅助线构造，进行转换求解．