初中第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数同步训练题

这是一份初中第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数同步训练题，文件包含九年级数学上册单元复习第二十二章二次函数知识精讲+考点例析+举一反三+实战演练原卷版docx、九年级数学上册单元复习第二十二章二次函数知识精讲+考点例析+举一反三+实战演练解析版docx、九年级数学上册单元复习第二十二章二次函数知识精讲+考点例析+举一反三+实战演练考试版docx等3份试卷配套教学资源，其中试卷共54页， 欢迎下载使用。
【高效培优】2022—2023学年九年级数学上册必考重难点突破必刷卷（人教版）
【单元复习】第二十二章 二次函数
（知识精讲+考点例析+举一反三+实战演练）
温馨提示：一分努力勤奋一份收获，必考重难点突破是培优最佳途径！
知识精讲
第二十二章 二次函数
一、二次函数的定义：
1.定义：一般地，如果是常数，，那么叫做的二次函数.
2.二次函数的性质
（1）抛物线的顶点是坐标原点，对称轴是轴.
（2）函数的图像与的符号关系.
①当时抛物线开口向上顶点为其最低点；
②当时抛物线开口向下顶点为其最高点.
（3）顶点是坐标原点，对称轴是轴的抛物线的解析式形式为.
二、二次函数的解析式
①一般式：(a、b、c为常数)，则称y为x的二次函数。
②顶点式：
③交点式（与x轴）：
三、抛物线的性质
①二次函数的图像是一条永无止境的抛物线。
②a，b，c为常数，a≠0，且a决定函数的开口方向，a>0时，开口方向向上，a0，当时，y随x的增大而减小；当时，y随x的增大而增大．若a0(a0，
∴开口向上，
∵h=3，k=1，
∴对称轴为：直线x=3；顶点坐标为：（3，1），
故选：B
【点睛】本题主要考查了二次函数顶点式的图象和性质，熟练地掌握顶点式的特征是解题的关键．二次函数，对称轴为：直线x=h；顶点坐标为：（h，k），当a>0时，开口向上，否则开口向下．
2．（2022·全国·九年级期末）如图，抛物线与x轴相交于点，与y轴相交于点C，小红同学得出了以下结论：①；②；③当时，；④．其中正确的个数为（       ）

A．4 B．3 C．2 D．1
【答案】B
【分析】根据二次函数的图像与性质，逐一判断即可．
【详解】解：∵抛物线与x轴交于点A、B，
∴抛物线对应的一元二次方程有两个不相等的实数根，
即，故①正确；
对称轴为，
整理得4a＋b＝0，故②正确；
由图像可知，当y＞0时，即图像在x轴上方时，
x＜－2或x＞6，故③错误，
由图像可知，当x＝1时，，故④正确．
∴正确的有①②④，
故选：B．
【点睛】本题考查二次函数的性质与一元二次方程的关系，熟练掌握相关知识是解题的关键．
3．（2022·全国·九年级期末）小明以二次函数的图象为灵感为某葡萄酒大赛设计了一款杯子，如图为杯子的设计稿，若，，则杯子的高CE为（       ）

A．12 B．11 C．6 D．3
【答案】A
【分析】首先由求出D点的坐标为（1，6），然后根据AB=4，可知B点的横坐标为x=3，代入抛物线方程，得到y=14，所以CD=14-6=8，又DE=4，所以可知杯子高度．
【详解】∵，
∴D点的坐标为(1,6)，抛物线的对称轴为x=1，
∵AB=4，
∴CB=CA=2，
∴B点的横坐标为：2+1=3，
代入B点横坐标即可求出B点的纵坐标，
∴当x=3时，，
∴B点纵坐标为14，
∵D点的纵坐标为6，
∴CD=14-6=8，
∴CE=CD+DE=8+4=12，
则杯子的高度为12，
故选：A．
【点睛】本题主要考查了二次函数的应用，求出顶点D和点B的坐标是解决问题的关键．
4．（2022·辽宁鞍山·中考真题）如图，在中，，，，，垂足为点，动点从点出发沿方向以的速度匀速运动到点，同时动点从点出发沿射线方向以的速度匀速运动．当点停止运动时，点也随之停止，连接，设运动时间为，的面积为，则下列图象能大致反映与之间函数关系的是（       ）

A． B．
C． D．
【答案】B
【分析】分别求出M在AD和在BD上时△MND的面积为S关于t的解析式即可判断．
【详解】解：∵∠ACB＝90°，∠A＝30°，，
∴∠B＝60°，，，
∵CD⊥AB，
∴，，，
∴当M在AD上时，0≤t≤3，
，，
∴，
当M在BD上时，3＜t≤4，
，
∴，
故选：B．
【点睛】本题考查了动点问题的函数图象，函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．
二、填空题（共4小题）
5．（2022·全国·九年级期末）在平面直角坐标．若点A，B是抛物线上两点，若点A，B的坐标分别为则m______n（填“＞”“＜”“＝”）
【答案】＞
【分析】求出抛物线的对称轴，开口方向，然后根据二次函数的增减性解答．
【详解】解：∵抛物线中，
a=－2＜0，，
∴抛物线开口向下，对称轴为直线x=－1，在对称轴右侧y随x的增大而减小，
∵点A、B的坐标分别为（3，m）、（4，n），且3＜4，
∴m＞n，
故答案为：＞．
【点睛】本题考查了二次函数图象上点的坐标特征，主要利用了二次函数的增减性，求出抛物线的对称轴是解题的关键．
6．（2022·全国·九年级期末）如图，抛物线交轴于、两点，交轴于点，点是抛物线上的点，则点关于直线的对称点的坐标为_________．

【答案】（0，1）
【分析】先求出A、B、C、D的坐标，根据CD∥x轴即可求出点关于直线的对称点坐标．
【详解】∵抛物线交轴于、两点，交轴于点，
∴当时，；
当时，
∴
∴OA=OC=5
∴
∵是抛物线上的点
∴，解得
当时，与A重合；
当时，；
∴CD∥x轴，
∴
设点关于直线的对称点M，则


∴M在y轴上，且△DCM是等腰直角三角形
∴DC=CM=6
∴M点坐标为（0，1）
故答案为：（0，1）．
【点睛】本题考查二次函数的性质，等腰直角三角形的判定与性质，解题的关键是根据对称得到△DCM是等腰直角三角形．
7．（2022·全国·九年级期末）如图，以一定的速度将小球沿与地面成一定角度的方向击出时，小球的飞行路线是一条抛物线．若不考虑空气阻力，小球的飞行高度（单位：m）与飞行时间（单位：s）之间具有函数关系：，则当小球飞行高度达到最高时，飞行时间_________s．

【答案】2
【分析】把一般式化为顶点式，即可得到答案．
【详解】解：∵h=-5t2+20t=-5（t-2）2+20，
且-5＜0，
∴当t=2时，h取最大值20，
故答案为：2．
【点睛】本题考查二次函数的应用，解题的关键是掌握将二次函数一般式化为顶点式．
8．（2022·辽宁·中考真题）如图，抛物线与x轴交于点和点，以下结论：
①；②；③；④当时，y随x的增大而减小．其中正确的结论有___________．（填写代表正确结论的序号）

【答案】①②##②①
【分析】根据二次函数的对称轴位置和抛物线开口方向确定①③，根据x＝-2时判定②，由抛物线图像性质判定④．
【详解】解：①抛物线的对称轴在y轴右侧，则ab＜0，而c＞0，故abc＜0，故正确；
②x＝-2时，函数值小于0，则4a-2b+c＜0，故正确；
③与x轴交于点和点，则对称轴，故，故③错误；
④当时，图像位于对称轴左边，y随x的增大而减大．故④错误；
综上所述，正确的为①②．
故答案为：①②．
【点睛】本题考查了二次函数的图像和性质，要求熟悉掌握函数与坐标轴的交点、顶点等点坐标的求法，及这些点代表的意义及函数特征．
二、简答题（共2小题）
9．（2022·浙江衢州·中考真题）如图1为北京冬奥会“雪飞天”滑雪大跳台赛道的横截面示意图．取水平线为轴，铅垂线为轴，建立平面直角坐标系．运动员以速度从点滑出，运动轨迹近似抛物线．某运动员7次试跳的轨迹如图2．在着陆坡上设置点（与相距32m）作为标准点，着陆点在点或超过点视为成绩达标．

(1)求线段的函数表达式（写出的取值范围）．
(2)当时，着陆点为，求的横坐标并判断成绩是否达标．
(3)在试跳中发现运动轨迹与滑出速度的大小有关，进一步探究，测算得7组与 的对应数据，在平面直角坐标系中描点如图3．
①猜想关于的函数类型，求函数表达式，并任选一对对应值验证．
②当v为多少m/s时，运动员的成绩恰能达标（精确到1m/s)？
（参考数据：，）
【答案】(1)（8≤x≤40）
(2)的横坐标为22.5，成绩未达标
(3)①a与成反比例函数关系，，验证见解析；②当m/s时，运动员的成绩恰能达标
【分析】（1）根据图像得出CE的坐标，直接利用待定系数法即可求出解析式；
（2）将代入二次函数解析式，由解出x的值，比较即可得出结果；
（3）由图像可知，a与成反比例函数关系，代入其中一个点即可求出解析式，根据CE的表达式求出K的坐标（32，4），代入即可求出a，再代入反比例函数即可求出v的值．
【详解】（1）解：由图2可知：，
设CE：，
将代入，
得：，解得，
∴线段CE的函数表达式为（8≤x≤40）．
（2）当时，，由题意得，
解得                                                          
∴的横坐标为22.5．
∵22.5＜32，
∴成绩未达标．
（3）①猜想a与成反比例函数关系．
∴设
将（100，0.250）代入得解得，
∴．
将（150，0.167）代入验证：，
∴能相当精确地反映a与的关系，即为所求的函数表达式．
②由K在线段上，得K（32，4），代入得，得
由得，
又∵，
∴，
∴当m/s时，运动员的成绩恰能达标．
【点睛】本题考查二次函数的应用，二次函数与一次函数综合问题，解题的关键在于熟练掌握二次函数的性质，并能灵活运用二次函数与一次函数的性质解决问题．
10．（2022·内蒙古鄂尔多斯·中考真题）如图，在平面直角坐标系中，抛物线y＝ax2+bx+2经过A（，0），B（3，）两点，与y轴交于点C．

(1)求抛物线的解析式；
(2)点P在抛物线上，过P作PD⊥x轴，交直线BC于点D，若以P、D、O、C为顶点的四边形是平行四边形，求点P的横坐标；
(3)抛物线上是否存在点Q，使∠QCB＝45°？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
【答案】(1)
(2)点的横坐标为1或2或或
(3)存在，点的坐标为或
【分析】（1）根据待定系数法，将点A，点B代入抛物线解析式，解关于b，c的二元一次方程组，即可求得抛物线的解析式；
（2）设出点P的坐标，确定出，由PD＝CO，列出方程求解即可；
（3）分Q在BC下方和Q在BC上方两种情况，过B作BH⊥CQ于H，过H作MN⊥y轴，交y轴于M，过B作BN⊥MH于N，证明△CHM≌△HBN，由全等三角形的性质得出CM＝HN，MH＝BN，求出H点的坐标，由待定系数法求出直线CH的解析式，联立直线CH和抛物线解析式即可得出点Q的坐标．
【详解】（1）解：将点代入得：，解得，则抛物线的解析式为．
（2）解：设点，对于二次函数，当时，，即，设直线的解析式为，将点代入得：，解得，则直线的解析式为，，，轴，轴，，∴当时，以、、、为顶点的四边形是平行四边形，，解得或或或，则点的横坐标为1或2或或．
（3）解：①如图，当Q在BC下方时，过B作BH⊥CQ于H，过H作MN⊥y轴，交y轴于M，过B作BN⊥MH于N，∴∠BHC＝∠CMH＝∠HNB＝90°，∴∠CHM+∠BHN＝∠HBN+∠BHN＝90°，∴∠CHM＝∠HBN，∵∠QCB＝45°，∴△BHC是等腰直角三角形，∴CH＝HB，∴△CHM≌△HBN（AAS），∴CM＝HN，MH＝BN，设点的坐标为，则，解得，即，设直线的解析式为，将点代入得：，解得，则直线的解析式为，联立直线与抛物线解析式得，解得或（即为点），则此时点的坐标为；②如图，当Q在BC上方时，过B作BH⊥CQ于H，过H作MN⊥y轴，交y轴于M，过B作BN⊥MH于N，同理可得：此时点的坐标为，综上，存在这样的点，点的坐标为或．
【点睛】本题是二次函数综合题，主要考查了待定系数法求函数解析式，平行四边形的判定，等腰直角三角形的性质和判定，全等三角形的性质和判定，二次函数图象上点的坐标特征，利用待定系数法确定出函数的解析式是解本题的关键．
实战演练
一、选择题（共4小题）
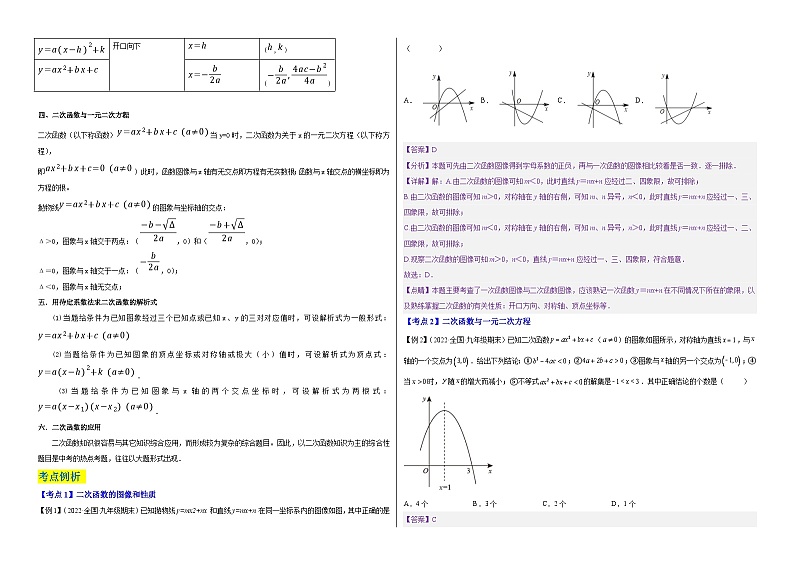
1．（2022·全国·九年级期末）二次函数的图象如图所示，则一次函数的图象大致是（     ）．

A． B． C． D．
【答案】D
【分析】根据二次函数的图象可以得到、的正负情况，从而可以得到一次函数的图象，本题得以解决．
【详解】解：由二次函数的图象可得，，，
一次函数的图象经过第一、二、三象限，
故选：D．
【点睛】本题考查二次函数的图象、一次函数的图象，解答本题的关键是明确题意，判断出系数的符号，再利用数形结合的思想解答．
2．（2022·全国·九年级期末）如图，是二次函数的图象，则下列结论正确的个数有（       ）
①；②；③二次函数最小值为；④．

A．1个 B．2个 C．3个 D．4个
【答案】A
【分析】根据抛物线与x轴的交点得到方程ax2+bx+c=0有两个根为-1，3，根据根与系数的关系可对①进行判断；由于x=-2时，y＞0，得到4a-2b+c＞0，然后把b=-2a代入计算，则可对②进行判断；由抛物线开口方向得a＞0，由抛物线的对称轴方程为x=1可对③进行判断；根据x=-1时，y=a-b+c=0，以及b=-2a，计算可对④进行判断．
【详解】解：∵二次函数的图象经过点（-1，0），（3，0），
∴方程ax2+bx+c=0有两个根为-1，3，
∴-1×3=-3