2023年河南省南阳市唐河县四校联考中考数学模拟试卷（二）（含解析）

这是一份2023年河南省南阳市唐河县四校联考中考数学模拟试卷（二）（含解析），共24页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
2023年河南省南阳市唐河县四校联考中考数学模拟试卷（二）一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）1.  下列说法正确的是(    )A. 任何有理数的绝对值一定是正数 B. 正数和负数统称为有理数
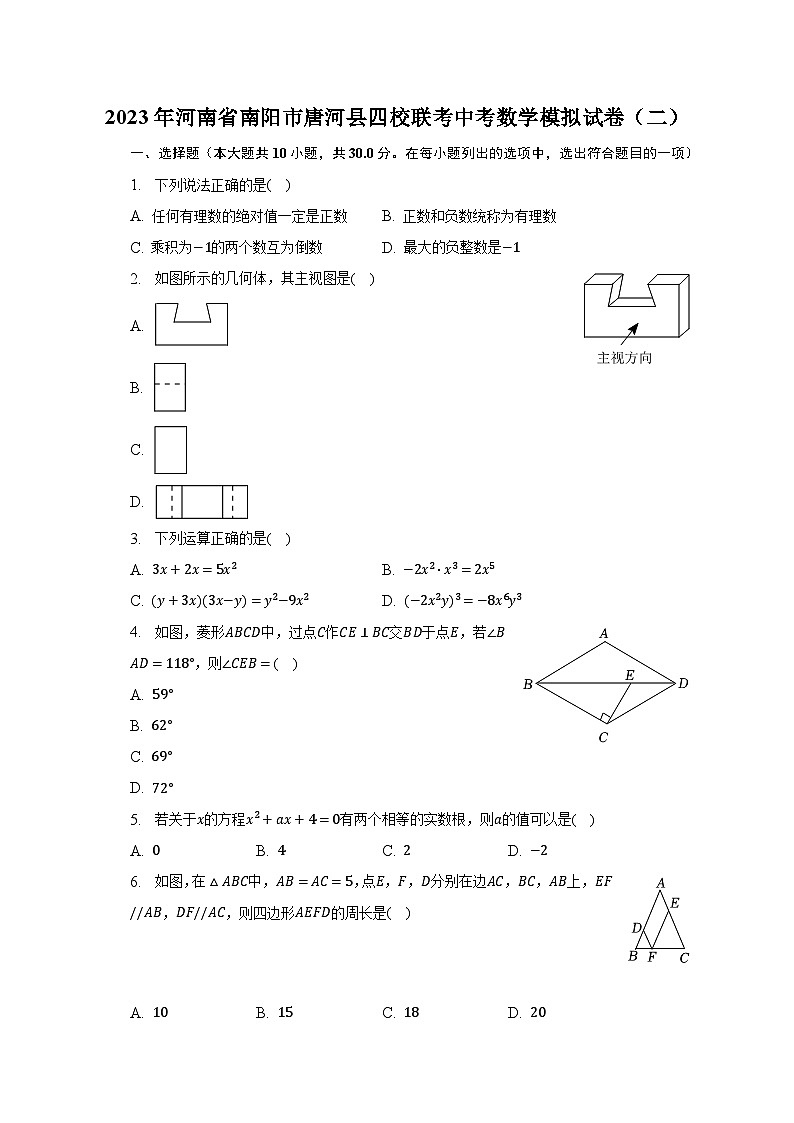
C. 乘积为的两个数互为倒数 D. 最大的负整数是2.  如图所示的几何体，其主视图是(    )A.
B.
C.
D. 3.  下列运算正确的是(    )A.  B.
C.  D. 4.  如图，菱形中，过点作交于点，若，则(    )A.
B.
C.
D. 5.  若关于的方程有两个相等的实数根，则的值可以是(    )A.  B.  C.  D. 6.  如图，在中，，点，，分别在边，，上，，，则四边形的周长是(    )
 A.  B.  C.  D. 7.  某班共有名学生，体育课上老师统计全班一分钟仰卧起坐的个数，由于小亮没有参加此次集体测试，因此计算其他名学生一分钟仰卧起坐的平均个数为个，方差为后来小亮进行了补测，成绩为个，关于该班名学生的一分钟仰卧起坐个数，下列说法正确的是(    )A. 平均个数不变，方差不变 B. 平均个数变小，方差不变
C. 平均个数变大，方差变大 D. 平均个数不变，方差变小8.  下列计算正确的是(    )A.  B.  C.  D. 9.  在平面坐标系中，正方形的位置如图所示，点的坐标为，点的坐标为，延长交轴于点，作正方形，延长交轴于点，作正方形，按这样的规律进行下去，第个正方形的面积为(    )
A.  B.  C.  D. 10.  在一次生活垃圾分类知识竞赛中，某校七、八年级各有名学生参加，已知七年级男生成绩的优秀率为，女生成绩的优秀率为，八年级男生成绩的优秀率为，女生成绩的优秀率为对于此次竞赛的成绩，下面有三个推断：
七年级男生成绩的优秀率小于八年级男生成绩的优秀率；
七年级学生成绩的优秀率一定小于八年级学生成绩的优秀率；
七、八年级所有男生成绩的优秀率一定小于七、八年级所有女生成绩的优秀率．
所有合理推断的序号是(    )A.  B.  C.  D. 二、填空题（本大题共5小题，共15.0分）11.  若代数式有意义，则实数的取值范围是______ ．12.  若，则的值是______．13.  不透明袋子中装有个球，其中有个绿球、个白球，这些球除颜色外无其他差别．从袋子中随机取出个球，则它是绿球的概率是______．14.  如图，在中，，，点在上，以点为圆心，长为半径的圆恰好与相切于点，分别交，于点，若，则阴影部分的面积是______ ．
 15.  如图，已知的半径为，是直径的延长线上一点，，是的一条弦，，以，为相邻两边作平行四边形，当，点在圆周上运动时，线段长的最小值是______ ．
三、计算题（本大题共1小题，共10.0分）16.  如图，在郑州世纪欢乐园，有一座直径米的摩天轮“伦敦之眼”，旋转周用时小明从摩天轮的底部与地面相距出发开始观光．
后小明离地面多高？
摩天轮转动周，小明在中所求的高度以上，会持续多长时间？

 四、解答题（本大题共7小题，共65.0分。解答应写出文字说明，证明过程或演算步骤）17.  本小题分
观察下列算式：
，，，
由此可推断：______；
请用含字母为正整数的等式表示中的一般规律______；
仿照以上方法解方程：．18.  本小题分
年初，为积极响应教育部“停课不停学”的号召，某中学组织本校优秀教师开展线上教学，经过近三个月的线上授课后，在五月初复学该校为了解学生不同阶段学习效果，决定随机抽取八年级部分学生进行两次跟踪测评，第一次是复学初对线上教学质量测评，第二次是复学一个月后教学质量测评根据第一次测试的数学成绩制成频数分布直方图图．
复学一个月后，根据第二次测试的数学成绩得到如下统计表： 成绩人数根据以上图表信息，完成下列问题：
______ ；
请在图中作出两次测试的数学成绩折线图，并对两次成绩作出对比分析用一句话概述；
某同学第二次测试数学成绩为分这次测试中，分数高于分的至少有多少人？至多有多少人？
请估计复学一个月后该校名八年级学生数学成绩优秀分及以上的人数．19.  本小题分
如图，矩形的顶点，分别在函数和的图象上，且．
求，的值；
若点，分别在和的图象上，且不与点，重合，是否存在点，，使得≌，若存在，请直接写出点，的坐标；若不存在，请说明理由．
20.  本小题分
学校要购入两种记录本，预计花费元，其中种记录本每本元，种记录本每本元，且购买种记录本的数量比种记录本的倍还多本．
求购买和两种记录本的数量；
某商店搞促销活动，种记录本按折销售，种记录本按折销售，则学校此次可以节省多少钱？21.  本小题分
“水幕电影”的工作原理是把影像打在抛物线状的水幕上，通过光学原理折射出图象，水幕是由若干个水嘴喷出的水柱组成的如图，水柱的最高点为，，，水嘴高．
以为坐标原点，所在的直线为轴，所在的直线为轴建立平面直角坐标系，求图中抛物线的解析式；
求水柱落点与水嘴底部的距离．
22.  本小题分
人教版教材中的折纸活动，引起了许多同学的兴趣在折纸的过程中，同学们不仅发展了空间观念，还积累了数学活动经验．
【操作】在矩形中，，，点在边上，连接，将沿折叠，点的对应点为．
【发现】如图，若点，，在同一条直线上，求证：为等腰三角形；
【探究】若点落在矩形对角线上，求的长；
【拓展】如图，过点作，当面积最大时，请直接写出的长．

 23.  本小题分
图是边长分别为和的两个等边三角形纸片和叠放在一起与重合的图形．

操作：固定，将绕点按顺时针方向旋转，连结，，如图，则 ______ 度，并直接写出线段与的数量关系______ ．
操作：若将图中的，绕点按顺时针方向旋转，使点、、在同一条直线上，连结、，如图．
线段与之间是否仍存在中的结论？若是，请证明；若不是，请直接写出与之间的数量关系；
求的度数．
若将图中的，绕点按逆时针方向旋转一个角，当等于多少度时，的面积最大？请直接写出答案．
答案和解析 1.【答案】 【解析】解：因为的绝对值是，既不是正数也不是负数，所以选项说法错误，故A选项不符合题意；
B.因为正数、负数和统称为有理数，所以选项说法错误，故B选项不符合题意；
C.因为乘积为的两个数互为倒数，所以选项说法错误，故C选项不符合题意；
D.因为最大的负整数是，所以选项说法正确，故D选项符合题意．
故选：．
A.应用绝对值的性质进行判定即可得出答案；
B.应用有理数的分类进行判定即可得出答案；
C.应用倒数的定义进行判定即可得出答案；
D.应用正数和负数的定义进行判定即可得出答案．
本题主要考查了有理数，绝对值，倒数，熟练掌握有理数，绝对值，倒数的定义进行求解是解决本题的关键．
 2.【答案】 【解析】解：从正面看，可得图形如下：

故选：．
根据从正面看得到的图形是主视图，可得答案．
本题考查了简单组合体的三视图，从正面看得到的图形是主视图．
 3.【答案】 【解析】解：、，故A不符合题意；
B、，故B不符合题意；
C、，故C不符合题意；
D、，故D符合题意；
故选：．
根据合并同类项，单项式乘单项式，平方差公式，幂的乘方与积的乘方法则，进行计算逐一判断即可解答．
本题考查了整式的混合运算，准确熟练地进行计算是解题的关键．
 4.【答案】 【解析】解：四边形是菱形，
，，
，
，
，
，
，
，
．
故选：．
根据菱形的性质得：，，根据等腰三角形的性质可得，由菱形的对角线平分线组对角可得，最后由直角三角形的两个锐角互余可得结论．
本题主要考查了菱形的性质，解题的关键是熟知菱形的对角线平分每一组对角．
 5.【答案】 【解析】解：根据题意得，
解得，，
即的值为或．
故选：．
根据根的判别式的意义得到，然后解的一元二次方程，从而可对各选项进行判断．
本题考查了根的判别式：一元二次方程的根与有如下关系：当时，方程有两个不相等的实数根；当时，方程有两个相等的实数根；当时，方程无实数根．
 6.【答案】 【解析】解：，，
四边形是平行四边形，
，，
，
，
，
，
，
，
同理可得，，
四边形的周长，
故选：．
根据平行四边形的判定得出四边形是平行四边形，进而利用平行四边形的性质解答即可．
此题考查平行四边形的判定和性质，关键是根据平行四边形的判定得出四边形是平行四边形解答．
 7.【答案】 【解析】解：小亮的成绩和其他人的平均数相同，都是个，
该班人的测试成绩的平均个数均为个，
新数据的每个数据与平均数差的平方和保持不变，而总人数在原数据的基础上增加，
新数据方差变小，
故选：．
根据平均数，方差的定义计算即可．
本题考查方差，算术平均数等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．
 8.【答案】 【解析】解：、，故A不符合题意；
B、与不属于同类项，不能合并，故B不符合题意；
C、，故C不符合题意；
D、，故D符合题意；
故选：．
利用同底数幂的除法的法则，合并同类项的法则，同底数幂的乘法的法则，幂的乘方的法则对各项进行运算即可．
本题主要考查同底数幂的除法，合并同类项，幂的乘方，同底数幂的乘法，解答的关键是对相应的运算法则的掌握．
 9.【答案】 【解析】解：点的坐标为，点的坐标为，
，，
设正方形的面积分别为，，
根据题意，得：，
，
，
∽，
在直角中，根据勾股定理，得：，
，
，
，，
，
，
，
，
，
，
，
，
，
由此可得：，
．
故选：．
首先设正方形的面积分别为，，由题意可求得的值，易证得∽，利用相似三角形的对应边成比例与三角函数的性质，即可求得的值，继而求得的值，继而可得规律：，则可求得答案．
此题考查了相似三角形的判定与性质、正方形的性质以及三角函数等知识．此题难度较大，解题的关键是得到规律．
 10.【答案】 【解析】解：七年级男生成绩的优秀率为，八年级男生成绩的优秀率为，
七年级男生成绩的优秀率小于八年级男生成绩的优秀率；
故正确，
七年级学生成绩的优秀率在与之间，八年级学生成绩的优秀率在在与之间，
不能确定哪个年级的优秀率大，
故错误；
七、八年级所有男生成绩的优秀率在与之间，七、八年级所有女生成绩的优秀率在与之间．
七、八年级所有男生成绩的优秀率一定小于七、八年级所有女生成绩的优秀率．
故正确．
故选：．
根据给出条件，利用统计学知识逐一加以判断．
本题考查统计学知识，属于中档题．
 11.【答案】 【解析】解：代数式有意义，
，
解得．
故答案为：．
根据分式有意义，分母不为，二次根式的被开方数是非负数列不等式解答即可．
此题主要考查了二次根式有意义的条件和分式有意义的条件，熟练掌握知识点是解题关键．
 12.【答案】 【解析】解：，
；
故答案为：．
利用完全平方公式把条件整体代入整理即可求解．
此题考查了因式分解，用到的知识点是完全平方公式，解题的关键是把的值整体代入求解．
 13.【答案】 【解析】解：不透明袋子中装有个球，其中有个绿球、个白球，
从袋子中随机取出个球，则它是绿球的概率是，
故答案为：．
用绿球的个数除以球的总数即可．
此题主要考查了概率公式，关键是掌握概率的求法：如果一个事件有种可能，而且这些事件的可能性相同，其中事件出现种结果，那么事件的概率．
 14.【答案】 【解析】解：连接，，
，，
，
长为半径的圆恰好与相切于点，
，
，
，
，
，
，
是等边三角形，
阴影部分的面积三角形的面积扇形的面积三角形的面积扇形的面积．
故答案为：．
连接，，根据三角形的内角和定理得到，根据切线的性质得到，求得，根据三角形和扇形的面积公式即可得到结论．
本题考查了切线的性质，扇形和三角形的面积的计算，等边三角形的判定和性质，正确地作出辅助线是解题的关键．
 15.【答案】 【解析】解：如图，连接，设交于点，连接，

四边形是平行四边形，
，，
，
在中，，，
，
，
，
，
的最小值为，最大值为，
，
的最小值为，最大值为．
故答案为：．
连接，设交于点，连接，求出，的值，利用三角形的三边关系即可解答．
本题考查的是垂径定理、勾股定理、三角形的三边关系等知识，解题的关键是熟练掌握基本知识、正确作出辅助线．
 16.【答案】解：旋转周用时，
后的度数为：，
，

延长交圆上点，过作于点，交圆于点，连接，
，，
，
，
，
答：后小明离地面；
．
上的点距离地面都是，
弧上的点都大于．
在中，
，，
．
．
．
摩天轮旋转周用时，
摩天轮旋转用时：．
答：摩天轮转动周，小明在中所求的高度以上，会持续． 【解析】延长交圆上点，过作于点，交圆于点，连接，根据题意可得，然后利用含度角的直角三角形即可求出后小明离地面的高度；
结合可得进而可得摩天轮转动周，小明在中所求的高度以上，会持续的时间．
本题考查了解直角三角形的应用，解决本题的关键是掌握含度角的直角三角形的性质．
 17.【答案】  【解析】解：根据题意得：；
根据题意得：；
方程整理得：，
即，
去分母得：，
解得：，
经检验是分式方程的解．
故答案为：；
观察已知等式得到所求即可；
归纳总结得到一般性规律，写出即可；
方程利用得出的规律变形，计算即可求出解．
此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．
 18.【答案】 【解析】解：由图可知，调查人数为人，
；
故答案为：；
折线图如下图所示，

复学后，学生的成绩总体上有了明显的提升；
某同学第二次测试数学成绩为分，
这次测试中，分数高于分的至少有人，
至多有人，
答：这次测试中，分数高于分的至少有人，至多有人；
人，
答：复学一个月后该校名八年级学生数学成绩优秀分及以上的有人．
根据频数之和为样本容量进行计算即可；
根据频数可绘制折线统计图；并根据折线的变化趋势得出判断；
根据频数分布情况进行“极值”判断即可；
求出“优秀”所占得百分比即可．
本题考查频数分布直方图，掌握频数、频率、总数之间的关系是解决问题的前提．
 19.【答案】解：将点的坐标代入得：；
过点作轴于点，过点作轴于点，

四边形为矩形，则，
，．
．
，
∽．
，则和的相似比为：：，
则，，
故点．
将点的坐标代入，得：．

、理由如下：
由知，两个反比例函数的表达式分别为：、，
假设存在点，符合题设条件，
设点，点，过点作轴于点，过点作轴于点，
如图：

由知，
．
所以，即．
所以，负值已舍去；
≌，
．
即且，
解得：或 或或，
由题意负值不合题意舍去，点不与点重合，不合题意舍去，
故；
故存在符合题设要求的点，，它们的坐标分别为、． 【解析】利用∽，得到；，从而求得点的坐标，进而求解；
  假设存在点、符合题设条件，由勾股定理构造方程即可求解．
本题考查了反比例函数综合应用，涉及到三角形相似、反比例函数的基本性质、勾股定理、解直角三角形等知识，综合性强，难度适中．
 20.【答案】解：设购买种记录本本，则购买种记录表本，
依题意，得：，
解得：，
，
答：购买种记录本本，种记录本本．
元．
答：学校此次可以节省元钱． 【解析】本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．
设购买种记录本本，则购买种记录表本，根据总价单价数量，即可得出关于的一元一次方程，解之即可得出结论；
根据节省的钱数原价优惠后的价格，即可求出结论．
 21.【答案】解：设抛物线的解析式为，
，
把代入得，
．
，
．
当时，．
解得，舍去．
所以．
答：水柱落点与水嘴底部的距离为． 【解析】据，顶点，设抛物线的解析式为，用待定系数法求解析式即可；
当时，求出的值解答即可．
本题主要考查了二次函数的应用，根据实际问题求出点的坐标，恰当选择抛物线解析式的形式是解决问题的关键．
 22.【答案】证明：将沿折叠，点的对应点为．
．
四边形是矩形，
．
，
，
，
是等腰三角形；
解：如图，当点落在上时，

四边形是矩形，
，
，，
．
将沿折叠，点的对应点为，
，
，
设，在中．，
解得，
；
如图，当点在上时，由，，可得垂直平分，

，
．

∽．
，
即，
解得；
综上所述，的长为或；
解：如图，过点作于点．
设，则，
，

，
，
，
当时，的面积最大．
设，
在中，，
化简整理得，
故． 【解析】根据折叠的性质得到根据矩形的性质得到根据平行线的性质得到，求得，根据等腰三角形的判定定理即可得到结论；
如图，当点落在上时，根据矩形的性质得到，根据勾股定理得到由翻折的性质可知，求得，设，在中根据勾股定理得到；如图，当点在上时，由，，可得垂直平分，根据相似三角形的性质即可得到；
如图，过点作于点设，则，根据完全平方公式和二次函数的性质即可得到结论．
本题是四边形的综合题，考查了矩形的性质，相似三角形的判定和性质，勾股定理，折叠的性质，分类讨论是解题的关键．
 23.【答案】   【解析】解：和是等边三角形，
，，
，
，
≌，，
全等三角形的对应边相等，
故答案为：，；
如图，

中结论仍然成立，理由如下：
和是等边三角形，
，
，
，
≌，
；
≌，
，
又，
；
如图，

当运动到，，

，
此时旋转角是，
，
当或．
，，，可求得；
方法同；
当边上的高最大时，的面积最大，高最大时的长，的面积最大，由两种情形．
本题考查了等边三角形的性质，全等三角形的判定和性质等知识，解决问题的关键是找全等的对应边和对应角，题目属于基础知识．