数学第二章 直角三角形的边角关系5 三角函数的应用同步达标检测题

这是一份数学第二章 直角三角形的边角关系5 三角函数的应用同步达标检测题，共9页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
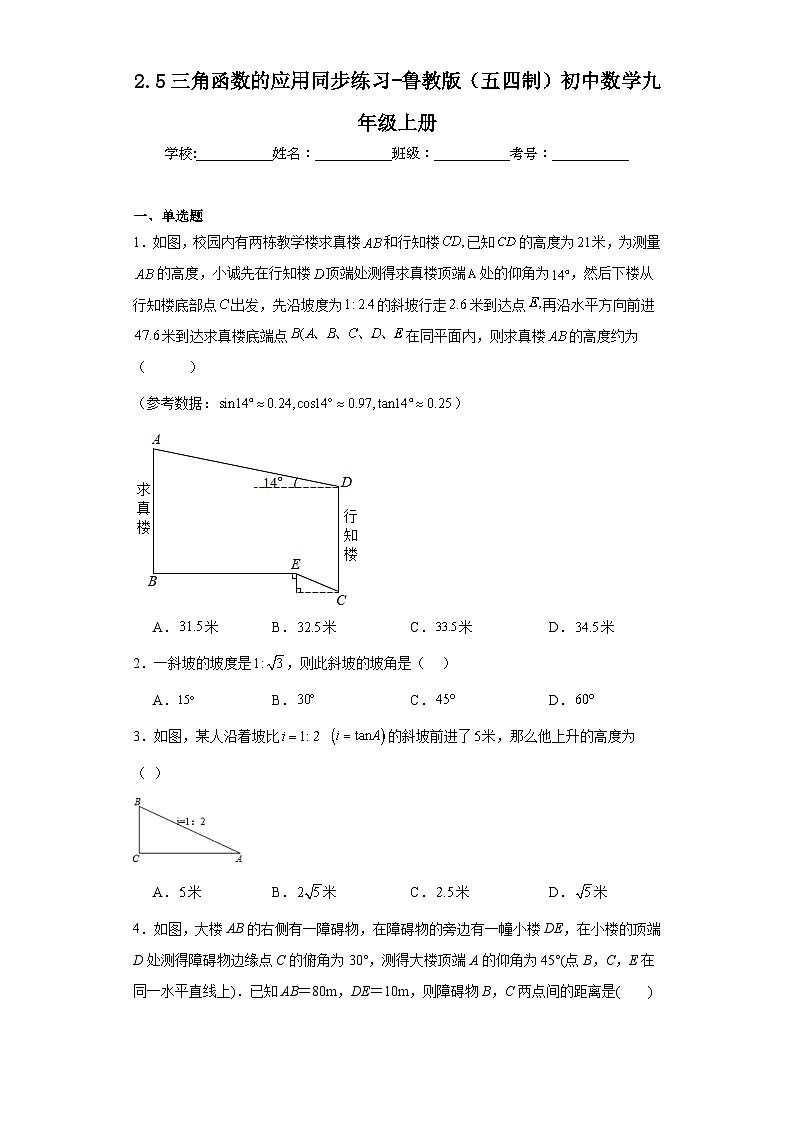
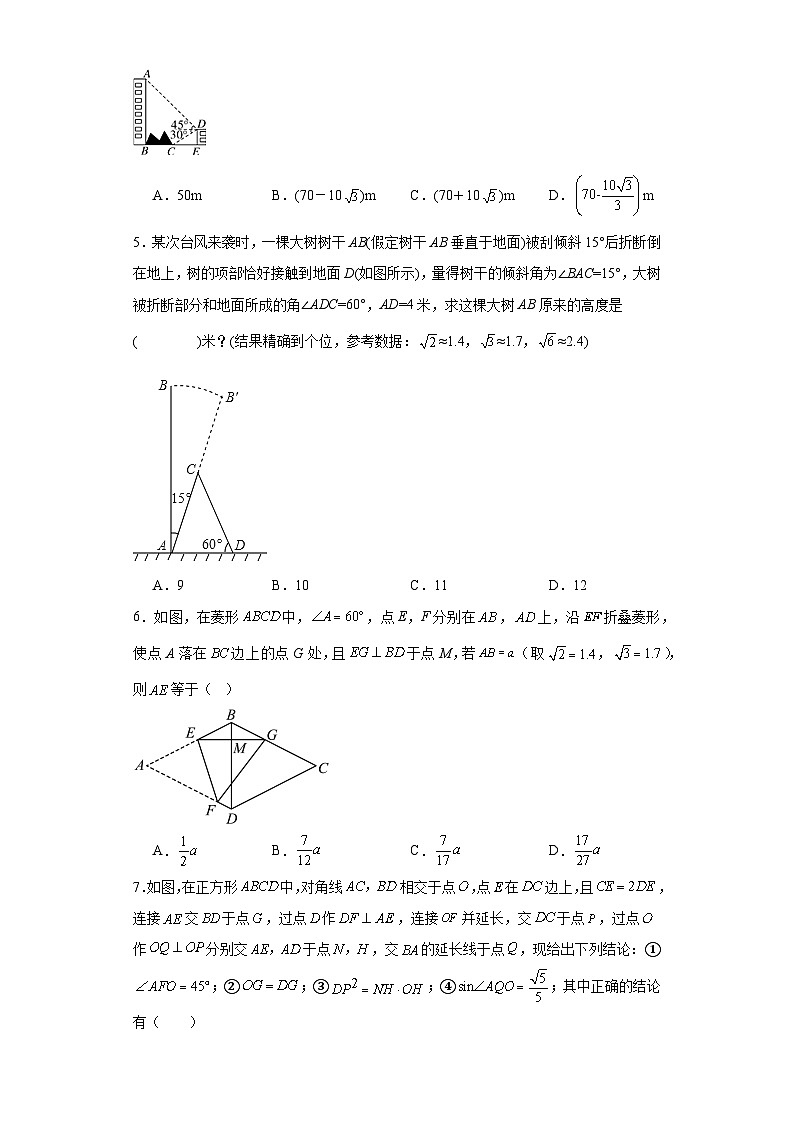
2.5三角函数的应用同步练习-鲁教版（五四制）初中数学九年级上册学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．如图，校园内有两栋教学楼求真楼和行知楼已知的高度为米，为测量的高度，小诚先在行知楼顶端处测得求真楼顶端处的仰角为，然后下楼从行知楼底部点出发，先沿坡度为的斜坡行走米到达点再沿水平方向前进米到达求真楼底端点在同平面内，则求真楼的高度约为（　　　）（参考数据：）A．米 B．米 C．米 D．米2．一斜坡的坡度是，则此斜坡的坡角是（    ）A． B． C． D．3．如图，某人沿着坡比 的斜坡前进了米，那么他上升的高度为（ ）A．米 B．米 C．米 D．米4．如图，大楼AB的右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°(点B，C，E在同一水平直线上)．已知AB＝80m，DE＝10m，则障碍物B，C两点间的距离是(　　)A．50m B．(70－10)m C．(70＋10)m D．m5．某次台风来袭时，一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断倒在地上，树的项部恰好接触到地面D(如图所示)，量得树干的倾斜角为∠BAC=15°，大树被折断部分和地面所成的角∠ADC=60°，AD=4米，求这棵大树AB原来的高度是(　　　　 )米？(结果精确到个位，参考数据：≈1.4，≈1.7，≈2.4)A．9 B．10 C．11 D．126．如图，在菱形中，，点E，F分别在，上，沿折叠菱形，使点A落在边上的点G处，且于点M，若（取，），则等于（   ）A． B． C． D．7．如图，在正方形中，对角线相交于点，点在边上，且，连接交于点，过点作，连接并延长，交于点，过点作分别交于点，交的延长线于点，现给出下列结论：①；②；③；④；其中正确的结论有（　　）A．①②③ B．②③④ C．①②④ D．①②③④8．如图，小明想测量教学楼的高度，他从距教学楼底部点水平距离为30米的A点处出发，沿坡度的斜坡行走了13米，到达二楼水平平台的处，继续行驶5米到达水平平台的处，从处观察教学楼顶端的仰角为53°（点A，，，，均在同一平面内），则教学楼的高度约为（    ）（参考数据：，，）A．22.1米 B．22.3米 C．17.1米 D．17.3米9．如图，一辆自行车竖直摆放在水平地面上，右边是它的部分示意图，现测得，，，则点A到的距离为（    ）A． B． C． D．10．河堤横断面如图所示，堤高BC＝6米，迎水坡AB的坡比是1∶，则AC的长是（  ）A．6米 B．12米C．3米 D．6米 二、填空题11．如图，当小杰沿着坡度的坡面由到直行走了26米时，小杰实际上升的高度      米（结论可保留根号）12．如图，一艘海轮位于灯塔P的北偏东方向，距离灯塔90海里的B处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东方向上的A处，这时，A处距离灯塔P有          海里．（，，，结果保留整数）  13．某河道要建一座公路桥，要求桥面离地面高度AC为3 m，引桥的坡角∠ABC为15°，则引桥的水平距离BC的长是__ __m．(精确到0.1 m；参考数据：sin15°≈0.258 8，cos15°≈0.965 9，tan15°≈0.267 9)14．如图．某同学为测量宣传牌的高度，他站在距离教学楼底部E处9米远的地面C处，测得宣传牌的底部B的仰角为60°，同时测得教学楼窗户D处的仰角为30°（A、B、D、E在同一直线上），然后，小明沿坡度的斜坡从C走到F处，此时正好与地面平行．他在F处又测得宣传牌顶部A的仰角为45°，则宣传牌的高度约为           米（结果精确到0.1米，）．  15．如图，为了测量电线杆AB的高度，小明将测量仪放在与电线杆的水平距离为9m的D处．若测角仪CD的高度为1.5m，在C处测得电线杆顶端A的仰角为36°，则电线杆AB的高度约为    （精确到0.1m）．（参考数据sin36°≈0.59．cos36°≈0.81，tan36°≈0.73）．16．如图，从一运输船的点A处观测海岸上高为41m的灯塔BC（观测点A与灯塔底部C在一个水平面上），测得灯塔顶部B的仰角为35°，则点A到灯塔BC的距离约为    （精确到1cm）．17．已知斜坡坡度为，如果斜坡长为米，那么斜坡的高为        米．18．已知晾衣架侧面伸缩部分如图1，由6根长方形铝条（厚度忽略不计），用9个钉子A，B，C，D，E，F，G，H，I链接而成，铝条宽度都为2cm，五根较长的长为42cm，其余一根长为22cm，每个钉子都在距离长方形铝条边为1cm的地方，主视图如图2所示．晾衣架伸缩时，点B在射线AP上滑动，∠ACB的大小也随之发生变化．记铝条ACE最右侧顶点为M，铝条IH最左侧顶点为N，当时，      ；当时，      ．（）19．如图，李老师用自制的直角三角形纸板去测量“步云阁”的高度，他调整自己的位置，设法使斜边 保持水平，边与点B在同一直线上，已知直角三角纸板中，测得眼睛D离地面的高度为米，他与“步云阁”的水平距离为，则“步云阁”的高度是           m．20．如图，大坝横截面的迎水坡AB的坡比为1：2，（即BC：AC=1：2），若坡面AB的水平宽度AC为12米，则斜坡AB的长为        米． 三、解答题21．如图，甲､乙两楼相距，甲楼高，自甲楼楼顶看乙楼楼顶，仰角为，乙楼有多高？（结果精确到）22．如图，已知锐角，且，点P为内部一点，矩形PQMN的边MN在射线OB上（点Q在点P左侧），MQ=4，MN=a，过点P作直线于点D，交射线OB于点E．（1）如图1，当矩形PQMN的顶点Q落在射线OA上时，若a=4，求DP的值．（2）如图2，当矩形PQMN的顶点Q落在内部时，连接OP交QM于点R，若，a=3，求的值．（3）连接DM、DQ，当与相似时，直接写出所有符合条件的a的值．23．某数学课外兴趣小组为了测量池塘对岸山丘上的塔的高度,在山脚下的广场处测得建筑物点(即山顶)的抑角为,沿水平方向前进245米到达点,测得建筑物顶部点的仰角为,已知山丘高182米,求塔的高度．(结果精确到0.1米,参考数据,,)24．常州天宁寺始建于唐贞观年间，是佛教音乐梵呗的发源地之一，也是常州最大的寺庙．某校数学兴趣小组的同学利用卷尺和自制的测角仪尝试求解天宁寺宝塔的高度．如图所示，平地上一幢建筑物AB与宝塔CD相距56m，在建筑物的顶部分别观测宝塔底部的俯角为45°、宝塔顶部的仰角为60°．求天宁寺宝塔的高度（结果保留根号）．
参考答案：1．B2．B3．D4．B5．B6．D7．D8．B9．A10．D11．12．7413．11.214．5.515．8.1 m．16．5917．6018．          32()19．20．21．22．（1）；（2）；（3）2或4或或．23．78.6米24．天宁寺宝塔的高度为米