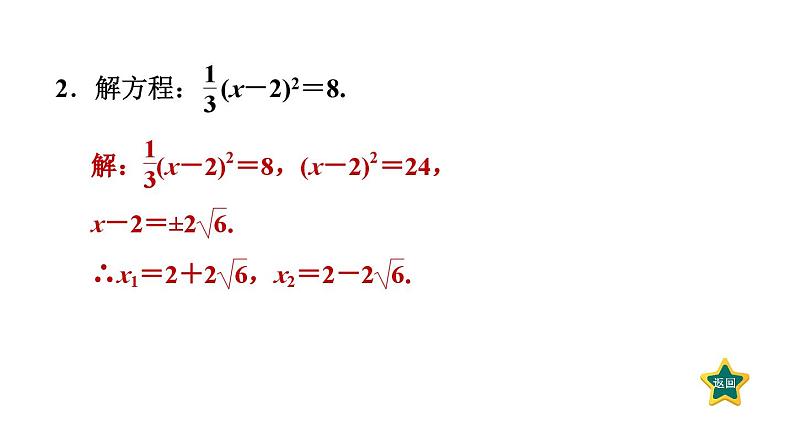
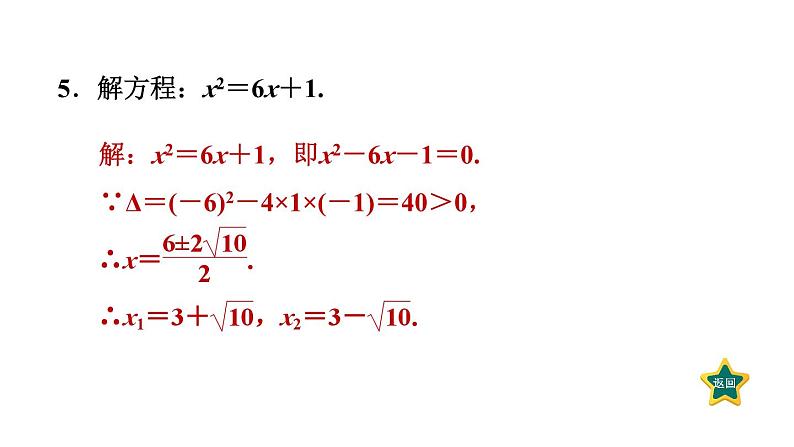
第2章 一元二次方程素养集训 一元二次方程的六种解法 作业课件

这是一份第2章 一元二次方程素养集训 一元二次方程的六种解法 作业课件，共15页。
第二章 一元二次方程素养集训一元二次方程的六种解法1．解方程：(4x－1)2＝225.2．解方程： (x－2)2＝8.3．解方程：x2＋4x＝5.解：x2＋4x＝5，x2＋4x＋4＝5＋4，即(x＋2)2＝9，则x＋2＝±3.∴x＝－2±3，即x1＝1，x2＝－5.4．【中考·梧州】解方程：2x2－4x－30＝0.解：2x2－4x－30＝0，x2－2x＝15，x2－2x＋1＝15＋1，(x－1)2＝16，x－1＝±4.∴x1＝5，x2＝－3.5．解方程：x2＝6x＋1.6．解方程： x－2＝2x2.7．【2021·罗湖区模拟】解下列方程：(1)x2＋4x－5＝0；解：∵x2＋4x－5＝0，∴(x＋5)(x－1)＝0，则x＋5＝0或x－1＝0，解得x＝－5或x＝1.(2)(x－3)2＝2(3－x)．解：∵(x－3)2＝2(3－x)，∴(x－3)2＋2(x－3)＝0，∴(x－3)(x－1)＝0，则x－3＝0或x－1＝0，解得x＝3或x＝1.8．解方程：3(x－5)2＝x2－25.【点技巧】先考虑直接开平方法和因式分解法，不能用这两种方法时，再用公式法，没有特殊要求的，尽量少用配方法．解：3(x－5)2＝x2－25，3(x－5)2＝(x＋5)(x－5)，3(x－5)2－(x＋5)(x－5)＝0，(x－5)[3(x－5)－(x＋5)]＝0，(x－5)(2x－20)＝0，x－5＝0或2x－20＝0.∴x1＝5，x2＝10.9．解方程：(x＋1)(x－1)＋2(x＋3)＝8.解：(x＋1)(x－1)＋2(x＋3)＝8，x2－1＋2x＋6＝8，x2＋2x＝3，x2＋2x＋1＝3＋1，(x＋1)2＝4，x＋1＝±2.∴x1＝1，x2＝－3.(1)根据材料解方程：x4＋x2－6＝0；(2)已知实数a，b满足(a＋2b)(a＋2b－2)＝2a＋4b－4，求4a＋8b－1的值．解：令a＋2b＝x，则原式可化为x(x－2)＝2x－4，解得x1＝x2＝2，即a＋2b＝2.∴4a＋8b－1＝4(a＋2b)－1＝4×2－1＝7.