还剩45页未读，
继续阅读
所属成套资源：2024届高考数学一轮总复习课件（70份）
成套系列资料，整套一键下载
2024届高考数学一轮总复习第三章三角函数解三角形第七讲正弦定理和余弦定理课件
展开这是一份2024届高考数学一轮总复习第三章三角函数解三角形第七讲正弦定理和余弦定理课件，共53页。PPT课件主要包含了三角形解的判断，答案AD，答案B，边是否相等，否相等，答案A，断三角形的形状，变式训练，方程求解，列方程求解等内容，欢迎下载使用。
1.正弦定理与余弦定理
3.三角形中常用的面积公式
【名师点睛】(1)三角形中的三角函数关系①sin (A＋B)＝sin C；②cs (A＋B)＝－cs C；
(2)三角形中的射影定理
在 ABC 中，a＝b cs C＋c cs B；b＝a cs C＋c cs A；c＝
b cs A＋a cs B.
(3) 在ABC 中，两边之和大于第三边，两边之差小于第三边，
A>B⇔a>b⇔sin A>sin B⇔cs A
2.(2023 年武功县期中)在△ABC 中，若三边之比 a∶b∶c＝
3.(2022 年全国乙卷文科)记△ABC 的内角 A，B，C 的对边分
别为 a，b，c，已知 sin C sin (A－B)＝sin B sin (C－A).
(1)若 A＝2B，求 C；(2)证明：2a2＝b2＋c2.
(1)解：由 sin C sin (A－B)＝sin B sin (C－A)，又 A＝2B，∴sin C sin B＝sin B sin (C－A)，∵sin B≠0，∴sin C＝sin (C－A)，即 C＝C－A(舍去)或 C＋C－A＝π，
(2)证明：由 sin C sin (A－B)＝sin B sin (C－A)，得 sin C sin A cs B－sin C cs A sin B＝sin B sin C cs A－sin B cs C sin A，由正弦定理可得 ac cs B－bc cs A＝bc cs A－ab cs C，
(1)求 c 的大小；(2)求 sin B 的值；
(3)求 sin (2A－B)的值.
【题后反思】解三角形问题的技巧
(1)解三角形时，如果式子中含有角的余弦或边的二次式，要考虑用余弦定理；如果式子中含有角的正弦或边的一次式时，则考虑用正弦定理，以上特征都不明显时，则要考虑两个定理都有可能用到.
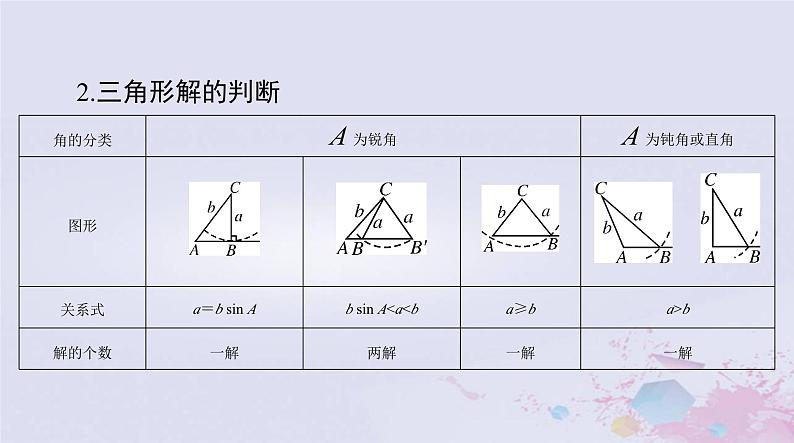
(2)三角形解的个数的判断：已知两角和一边，该三角形是确定的，其解是唯一的；已知两边和一边的对角，该三角形具有不唯一性，通常根据三角函数值的有界性和大边对大角定理进行判断.
考点二 判断三角形的形状
A.钝角三角形C.锐角三角形
B.直角三角形D.等边三角形
又 B∈(0，π)，所以 sin B>0，所以 sin C
边)，则△ABC 的形状为(
A.直角三角形B.等边三角形C.等腰三角形或直角三角形D.等腰直角三角形
即 a2＋c2－b2＝2a2，
所以 a2＋b2＝c2.所以△ABC 为直角三角形，无法判断两直角
又 sin A＝sin (B＋C)＝sin B cs C＋cs B sin C，所以 cs B sin C＝sin B cs C＋cs B sin C，即 sin B cs C＝0，又 sin B≠0，
所以 cs C＝0，又角 C 为三角形的内角，
【题后反思】判断三角形形状的常用技巧若已知条件中既有边又有角，则
(1)化边：通过因式分解、配方等得出边的相应关系，从而判
(2)化角：通过三角恒等变换，得出内角的关系，从而判断三
角形的形状.此时要注意应用 A＋B＋C＝π这个结论.
考点三 与三角形面积、周长有关的问题
考向 1 与三角形面积有关的问题
[例 2](2022 年太原市模拟)已知 a，b，c 分别是△ABC 的内角A，B，C 所对的边，3c sin A＝4b sin C，再从下面条件①与②中任选一个作为已知条件，完成以下问题.
注：如果选择多个条件分别解答，则按第一个解答计分.
(1)证明：△ABC 为等腰三角形；
，点 D 在线段 AB 上，且 BD＝
(2)若△ABC 的面积为 22DA，求 CD 的长.
【题后反思】(1)求三角形面积的方法
①若已知三角形的一个角(角的大小或该角的正、余弦值)及该
②若已知三角形的三边，可先求其一个角的余弦值，再求其正弦值，代入(1)中公式求面积.总之，结合图形选择恰当的面积公式是解题的关键.
(2)已知三角形面积求边、角的方法
①若求角，就寻求夹这个角的两边的关系，利用面积公式列
②若求边，就寻求与该边(或两边)有关联的角，利用面积公式
考向 2 与三角形周长有关的问题
则(b＋c)2≤64，即 b＋c≤8(当且仅当 b＝c＝4 时等号成立)，∴△ABC 周长＝a＋b＋c＝4＋b＋c≤12，即△ABC 周长的最大值为 12.答案：12
1.(考向 1)(2021 年密云区月考)设△ABC的内角 A，B，C 的对
边分别为a，b，c.已知b2＋c2＝a2＋bc，求：
(2)若a＝2，求△ABC面积的最大值.
(1)证明：在△ABC中，因为sin C sin (A－B)＝sin B sin (C－A)，所以 sin C(sin A cs B－cs A sin B)＝sin B(sin C cs A－cs C sin A)，
所以 sin A sin B cs C＋sin A cs B sin C＝2cs A sin B sin C，即 sin A(sin B cs C＋cs B sin C)＝2cs A sin B sin C，所以 sin A sin (B＋C)＝2cs A sin B sin C，
即sin 2A＝2cs A sin B sin C.由正弦定理得a2＝2bc·cs A，由余弦定理得a2＝b2＋c2－2bc cs A，所以2a2＝b2＋c2.
(2)求 CD 的长.
(1)求 sin ∠BCE 的值；
【反思感悟】平面几何图形中研究或求与角有关的长度、角度、面积的最值、优化设计等问题，通常是转化到三角形中，利用正、余弦定理通过运算的方法加以解决.在解决某些具体问题时，常先引入变量，如边长、角度等，然后把要解三角形的边或角用所设变量表示出来，再利用正、余弦定理列出方程，解之，若研究最值，常使用函数思想.
(2023 年安阳市期中)如图 3-7-2 所示，在平面四边形ABCD中，
(1)求 tan∠BDC 的值；(2)求 BD.
相关课件
高考数学一轮总复习课件第3章三角函数解三角形第7讲正弦定理和余弦定理（含解析）：
这是一份高考数学一轮总复习课件第3章三角函数解三角形第7讲正弦定理和余弦定理（含解析），共50页。PPT课件主要包含了计算Rr，题组三真题展现，答案D，答案AD，图3-7-1，题后反思，答案A，答案B，变式训练，答案12等内容，欢迎下载使用。
2024届高考数学一轮总复习第三章三角函数解三角形第五讲三角函数的图象与性质课件：
这是一份2024届高考数学一轮总复习第三章三角函数解三角形第五讲三角函数的图象与性质课件，共49页。PPT课件主要包含了常用结论，答案D，图D18，答案B，答案A，答案C，题后反思，考法全练，式求解，高分训练等内容，欢迎下载使用。
2024年高考数学一轮复习第三章第七讲正弦定理和余弦定理课件：
这是一份2024年高考数学一轮复习第三章第七讲正弦定理和余弦定理课件，共53页。PPT课件主要包含了三角形解的判断，答案AD，答案B，边是否相等，否相等，答案A，断三角形的形状，变式训练，方程求解，列方程求解等内容，欢迎下载使用。
