四川省宜宾市叙州区第二中学2023届高三数学（理）适应性考试试题（Word版附解析）

这是一份四川省宜宾市叙州区第二中学2023届高三数学（理）适应性考试试题（Word版附解析），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
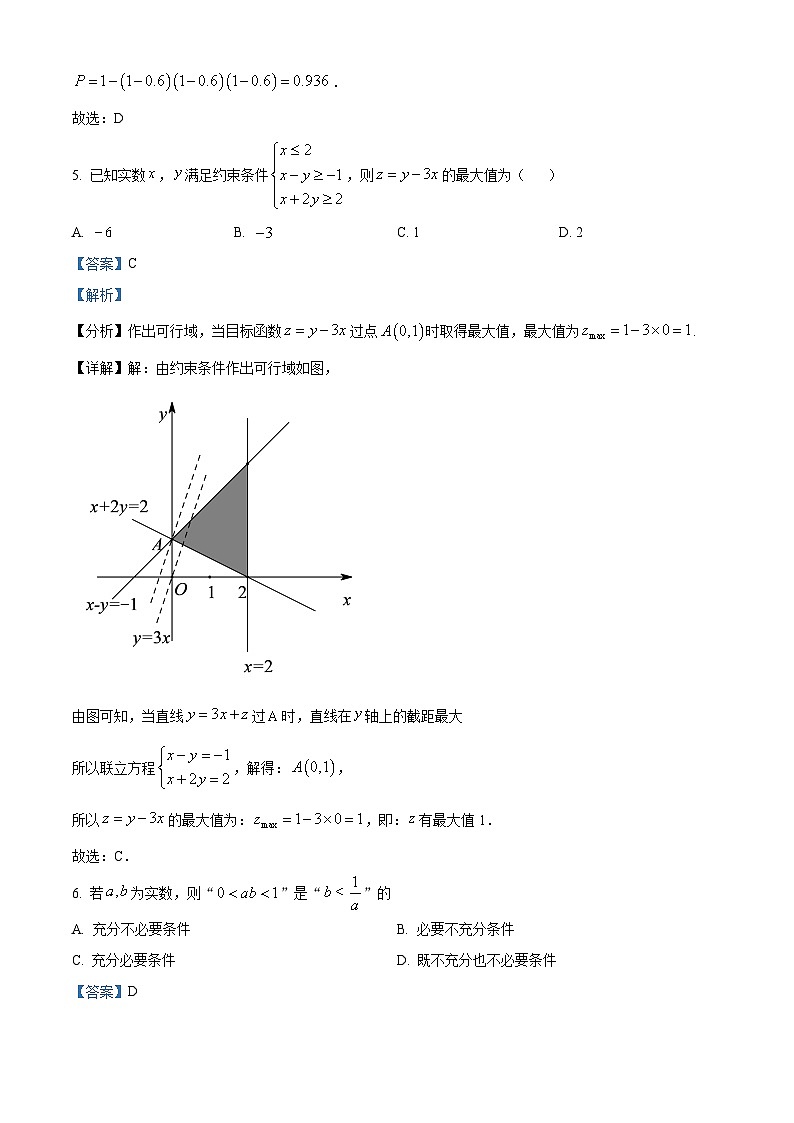
叙州区二中高2020级高考适应性考试数学（理工类）第I卷  选择题（60分）一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知集合，，则下列判断正确的是（    ）A.  B.  C.  D. 【答案】D【解析】【分析】用列举法写出集合，再根据集合间的关系与集合的交集运算求解即可．【详解】解：，，，，故选：D．2. 已知复数，其中为虚数单位，则（    ）A.  B.  C.  D. 【答案】D【解析】【分析】本题首先可根据复数的除法运算得出，然后通过共轭复数的性质得出，最后两者相加，即可得出结果.【详解】因为，所以，，，故选：D.3. 空气质量指数(AQI)是描述空气清洁或者污染的程度，是对二氧化硫、二氧化氮、PM10、PM2.5、一氧化碳和臭氧这6项污染物的统一评价.AQI在空气为优，在空气为良，在为轻度污染，在为中度污染，在为重度污染，300以上为严重污染.如图为我国34个省级行政区某日的AQI数据条形图.给出下列结论：①当日超过半数以上的省级行政区空气为良；②当日省级行政区空气被污染的比例超过20%；③当日我国各省级行政区AQI的平均值小于100(同一组中的数据用该组区间的中点值作代表).其中正确的个数为（    ）A. 0 B. 1 C. 2 D. 3【答案】C【解析】【分析】利用我国34个省级行政区某日的AQI数据条形图中的数据对3个命题分别经观察、计算、比较而得解.【详解】由图中数据可知，34个省级行政区中空气为良的有18个，故①正确；空气被污染的省级行政区个数为5+1=6，，故②不正确；当日我国34个省级行政区AQI的平均值为，故③正确，共有2个正确的命题.故选：C4. “三个臭皮匠顶个诸葛亮”是一句俗语，比喻人多智慧多．假设每个“臭皮匠”单独解决某个问题的概率均为，现让三个“臭皮匠”分别独立处理这个问题，则至少有一人解决该问题的概率为（    ）A.  B.  C.  D. 0．936【答案】D【解析】【分析】由相互独立事件的概率公式可得三个臭皮匠都没有解决问题的概率，由对立事件的概率性质计算可得答案.【详解】“至少有一人解决该问题”的对立事件为“三人都未解决”，故所求的概率为．故选：D5. 已知实数，满足约束条件，则的最大值为（    ）A.  B.  C. 1 D. 2【答案】C【解析】【分析】作出可行域，当目标函数过点时取得最大值，最大值为.【详解】解：由约束条件作出可行域如图，由图可知，当直线过时，直线在轴上的截距最大所以联立方程，解得：，所以的最大值为：，即：有最大值1．故选：C．6. 若为实数，则“”是“”的A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件 D. 既不充分也不必要条件【答案】D【解析】【详解】若“0＜ab＜1”，当a，b均小于0时，b＞即“0＜ab＜1”⇒“b＜”为假命题；若“b＜当a＜0时，ab＞1，即“b＜”⇒“0＜ab＜1”为假命题，综上“0＜ab＜1”是“b＜”的既不充分也不必要条件，故选D7. 函数的图象大致是（    ）A.  B. C.  D. 【答案】D【解析】【分析】根据函数为偶函数，以及在时的单调性即可由排除法解出．【详解】因为函数的定义域为，而，所以函数为偶函数，其图象关于轴对称，所以错误；当时，，由可得，所以函数在上递减，在上递增，所以错误；而，排除，所以正确．故选：D．8. 在等差数列{an}中，若a6+a10=18，a3+a5+a13=12，则使an>100成立的正整数n的最小值为（    ）A. 24 B. 25 C. 26 D. 27【答案】D【解析】【分析】由已知建立关于首项和公差的方程组，解之可求得数列的通项，由此可得选项．【详解】解：设等差数列{an}的公差为，∵在等差数列{an}中，a6+a10=18，a3+a5+a13=12，∴，解得a1=﹣26，d=5，∴an=﹣26+5(n﹣1)=5n﹣31，由5n﹣31>100，得，∴使an>100成立的正整数n的最小值为27．故选：D．9. 已知函数，且，则（    ）A.  B.  C.  D. 3【答案】C【解析】【分析】令，则为奇函数，根据已知求出，，再由即可求出答案.【详解】解：根据题意，函数，则，则有，故，若，则，故选：C.10. 已知函数f(x)＝2sin2x（sin2x+cos2x）﹣1，则下列说法正确的是（    ）A. f(x)的最小正周期为πB. f(x)的最大值为2C. f(x)在[0，]上是增函数D. f(x)在[0，]上有4个零点【答案】C【解析】【分析】利用二倍角公式以及辅助角公式可得f(x)＝2sin2x（sin2x+cos2x）﹣1＝sin（4x﹣），再由三角函数性质即可求解.【详解】解：函数f(x)＝2sin2x（sin2x+cos2x）﹣1＝2sin22x﹣1+2sin2xcos2x＝sin4x﹣cos4x＝sin（4x﹣）．所以函数的周期为：T＝＝，所以A不正确；函数的最大值为，所以B不正确；，解得，所以f(x)在[0，]上是增函数，所以C正确；f(x)在[0，]上有2个零点，所以D不正确．故选：C．11. 已知抛物线，过焦点且倾斜角为的直线交抛物线于两点，以为直径的圆与抛物线的准线相切，切点的纵坐标是，则抛物线的准线方程为（    ）A.  B.  C.  D. 【答案】B【解析】【分析】设直线的方程为与抛物线联解，利用为直径的圆与抛物线的准线相切，切点的纵坐标是得到得解【详解】抛物线的焦点坐标为，准线方程为，直线的方程为因为切点的纵坐标是,所以圆心的纵坐标为,即中点的纵坐标为由得，代入直线方程得即则则则则准线方程为故选：B【点睛】涉及抛物线几何性质的问题常结合图形思考，通过图形可以直观地看出抛物线的顶点、对称轴、开口方向等几何特征，体现了数形结合思想解题的直观性．12. 已知函数，若恒成立，则的取值范围为 （    ）A.  B.  C.  D. 【答案】D【解析】【分析】利用导数研究函数的单调性，再利用导数解决不等式恒成立问题，根据数形结合的思想方法即可得出结果.【详解】的定义域为，，令，解得，当时，，单调递增，当时，，单调递减，又所以的图像如图所示，令，恒过定点要使，必有图像恒在图像的下方，则，当与的图像相切于点时，m取得最小值.当时，，令，则，所以此时切线斜率为-1，故，故选：D  第II卷  非选择题（90分）二、填空题：本题共4小题，每小题5分，共20分．13. 的展开式中的系数为___________.【答案】840【解析】【分析】根据的展开式的通项公式可得的展开式中的系数.【详解】展开式中的系数为故答案为：84014. 已知圆的圆心坐标是，若直线与圆相切于点，则圆的标准方程为___________.【答案】【解析】【分析】由题意画出图形，利用圆心与切点的连线与切线垂直求得m，再求半径，即可写出圆的方程．【详解】解：如图所示，  由圆心与切点的连线与切线垂直，得，解得.所以圆心为，半径为.所以圆的标准方程为.故答案为：.15. 用0、1、2、3、4、5这六个数字组成一个无重复数字的五位数，百位和个位必须是奇数的数有_______个．【答案】108【解析】【分析】先安排个位和百位上的数字，再安排万位上的数字，最后安排剩下的位置上的数字即可.【详解】根据题意，可以分三步完成：第一步，先安排个位和百位上的数字，从3个奇数中选两个排序，有种方案；第二步，安排万位上的数字，不能有0，故需要在剩下的3个数字中选1个安排，有种方案；第三步，最后安排十位和千位的数字，此时还有三个数字，只需从三个数字中选两个排列，故有种方案.所以根据分步乘法计数原理即可得个满足条件的数.故答案为：16. 已知双曲线的左、右焦点分别为，过的直线与圆相切于点，且直线与双曲线的右支交于点，若，则双曲线的离心率为________．【答案】##【解析】【分析】数形结合可知，，且，利用中边的关系即可求得离心率.【详解】如图所示：由题可知，，，则，又，，又，则，作交于点，可得，，则.在中，，即，得，又，化简可得，，双曲线的离心率为.故答案为：.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分.17. 如图，平面四边形内接于一个圆，且，，为钝角，.（1）求；（2）若，求的面积.【答案】（1）；（2）.【解析】【分析】（1）在中，根据题中数据，由正弦定理求出，进而可到余弦值；（2）先根据四边形有外接圆，得到，求出，在中，由余弦定理求出，再由三角形面积公式，即可得出结果.【详解】（1）在中，，，，由正弦定理可得，即，解得；又为钝角，所以为锐角，则；（2）由平面四边形内接于一个圆可得，所以，又为钝角，所以为锐角，则，在中，由余弦定理可得，即，整理得，解得，则的面积为.18. 如图，在几何体中，四边形是矩形，平面，，，，，分别是线段，，的中点．（1）求证：平面平面；（2）求平面与平面所成二面角的正弦值．【答案】（1）证明见解析；（2）．【解析】【分析】（1）先证明平面，平面，利用判定定理证明平面平面；（2）以为原点，分别以，，的方向为轴，轴，轴的正方向，建立空间直角坐标系用向量法求平面与平面所成二面角的正弦值．【详解】（1）如图，因为中点为，连接，又是的中点，可知，又平面，平面，所以平面．在矩形中，由，分别是，的中点得．又平面，平面，所以平面．又因为，平面，平面，所以平面平面（2）如图，在平面内，过点作，因为，所以．又因为平面，所以，．以为原点，分别以，，的方向为轴，轴，轴的正方向，建立空间直角坐标系，则，，，因为平面，所以为平面的法向量，设为平面的法向量．又，，由得取得．从而所以平面与平面所成二面角的正弦值为．【点睛】立体几何解答题的基本结构：(1)第一问一般是几何关系的证明，用判定定理；(2)第二问是计算，求角或求距离（求体积通常需要先求距离），通常可以建立空间直角坐标系，利用向量法计算．19. 我国探月工程嫦娥五号探测器于2020年12月1日23时11分降落在月球表面预选着陆区，在顺利完成月面自动采样之后，成功将携带样品的上升器送入到预定环月轨道，这是我国首次实现月球无人采样和地外天体起飞，对我国航天事业具有重大而深远的影响．某校为了解高中生的航空航天知识情况，设计了一份调查问卷，从该校高中生中随机抽取部分学生参加测试，记录了他们的分数，将收集到的学生测试的评分数据按照[30，40），[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]分组，绘制成评分频率分布直方图，如下：（1）在测试评分不低于80分的12名学生中随机选取3人作为航空航天知识宣传大使，记这3名学生中测试评分不低于90分的人数为X，求X的分布列；（2）为激励学生关注科技，该校科技社团预在高一学年1000名学生中，举办航天知识大赛，计划以知识问答试卷形式，以分数高低评比等级，一等奖、二等奖奖励为航天模型，三等奖无奖品，且一等奖奖品价值为二等奖的二倍，每个等级都颁发相应证书．奖品费用需社团自行联系商家赞助，已筹集到赞助费6000元．现以问卷调查结果的频率估计竞赛结果，以在测试评分不低于90分频率记为一等奖获奖概率，不低于80分不足90分频率记为二等奖获奖概率，不低于70分不足80分频率记为三等奖获奖概率，若要求赞助费尽量都使用，试估计二等奖奖品的单价应为多少元？【答案】（1）答案见解析；（2）二等奖奖品单价为10元．【解析】【分析】（1）先计算出[80，90）和[90，100]的人数，然后求出X的可能取值，进而求出对应概率，即可列出分布列；（2）设未知数列不等式，解不等式即可.【详解】解：（1）不低于80分的12名学生中[80，90）：12×＝8（人）；低于80分的12名学生中[90，100]：12×＝4（人）；∴X的可能取值为0，1，2，3，∴P（X＝0）＝；P（X＝1）＝；P（X＝2）＝；P（X＝3）＝；分布列如下：x0123p（2）不低于90分的人数为：1000×0.015×10＝150；不低于80不足90的人数为：100×0.03×10＝300；设二等奖的奖品单价为x元，则一等奖奖品单价为2x元，则有300x+2×x×150≤6000，解得x≤10，又因为要求赞助费尽量都使用，所以x取10，即二等奖奖品单价为10元．20. 已知抛物线的焦点F到其准线的距离为4，椭圆经过抛物线的焦点F．（1）求抛物线的方程及a；（2）已知O为坐标原点，过点的直线l与椭圆相交于A，B两点，若，点N满足，且最小值为，求椭圆的离心率．【答案】（1）；    （2）【解析】【分析】(1)由条件列方程求，由此可得抛物线方程及其焦点坐标，再由条件求，(2)联立方程组，利用设而不求法结合条件求出点的轨迹，列方程求，由此可得离心率.【小问1详解】抛物线的焦点F到其准线的距离为4可得抛物线的方程：椭圆经过抛物线的焦点椭圆右顶点为，所以．【小问2详解】①当直线斜率存在时，设直线方程为由得，∵∴，即∴∴，∴又∵∴，即∴∴N点轨迹为直线②当直线斜率不存在时，经检验点在直线上．∴N点轨迹方程为最小值即点O到直线的距离∴，即椭圆的离心率为．【点睛】解决直线与椭圆的综合问题时，要注意：(1)注意观察应用题设中的每一个条件，明确确定直线、椭圆的条件；(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题．21. 已知函数.（1）当时，判断的单调性；（2）若时，设是函数的零点，为函数极值点，求证：.【答案】（1）在单调递增；    （2）证明见解析.【解析】【分析】（1）对函数求导，令再次求导，判断导函数的单调性以及正负取值情况，进而得到原函数的单调性；（2）首先研究函数的单调性，根据零点存在性定理确定其零点，并且表示出，再运用赋值法求出，再次运用函数的单调性确定其取值情况，进而证出结论.【小问1详解】当时，，所以，令，， ，即，在单调递增，，即，在单调递增；【小问2详解】由于，设，，当时，，则在为减函数；当时，，则在为增函数；，当，，所以存在，使得，即，所以，所以在上单调递减，在上单调递增，，当，，所以在区间必存在一个零点，令，则：，设，则，由（1）知，，所以在为增函数，，所以，根据零点存在判定定理可知，即.【点睛】关键点点睛：（1）运用导数研究函数的单调性时，一次求导得不出导函数正负取值情况时，可以进行二次求导判断一阶导函数的单调性以及取值情况，进而得到原函数的单调性；（2）本题主要考查零点问题，所以零点存性定理要灵活使用；（3）运用导数对不等式证明时还是要根据函数的单调性；（4）注意保证运算的正确性.（二）选考题：共10分．请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分．（选修4-4 极坐标与参数方程）22. 在平面直角坐标系xOy中，曲线的参数方程为其中t为参数，，曲线的参数方程为（为参数）．以坐标原点O为极点，x轴非负半轴为极轴，建立极坐标系．（1）求曲线，的极坐标方程；（2）若，曲线，交于M，N两点，求的值．【答案】（1），    （2）【解析】【分析】（1）消去参数，可得曲线的直角坐标方程，再利用极坐标与直角坐标的互化公式可求出曲线的极坐标方程，同理可求出曲线的极坐标方程，（2）将代入曲线的极坐标方程，化简后利用根与系数的关系，再结合极坐标的几何意义可求得结果【小问1详解】依题意，曲线普通方程为，即曲线的极坐标方程为．曲线的普通方程为，即，故曲线的极坐标方程为．【小问2详解】由，得，将代入曲线的极坐标方程中，可得，设上述方程的两根分别是，，则，，故．（选修4-5 不等式选讲）23. 已知函数．（1）当m＝2时，解不等式；（2）若函数有三个不等实根，求实数m的取值范围．【答案】（1）    （2）【解析】【分析】（1）利用零点分段法解绝对值不等式；（2）有三个不等实根转化为有两个大于0的实根，列出不等式组，求出实数m的取值范围.【小问1详解】当m＝2时，，，解得：或综上：不等式的解集为.【小问2详解】由题意得：有三个不等实根，令，则与有三个交点，结合函数图象可知，满足要有两个交点，即有两个大于0的实根，故，解得：所以实数m的取值范围是.