【中职专用】高中数学 人教版2021·基础模块上册 3.2.1一次函数模型（教案）

这是一份【中职专用】高中数学 人教版2021·基础模块上册 3.2.1一次函数模型（教案），共6页。教案主要包含了一次函数图像和性质等内容，欢迎下载使用。
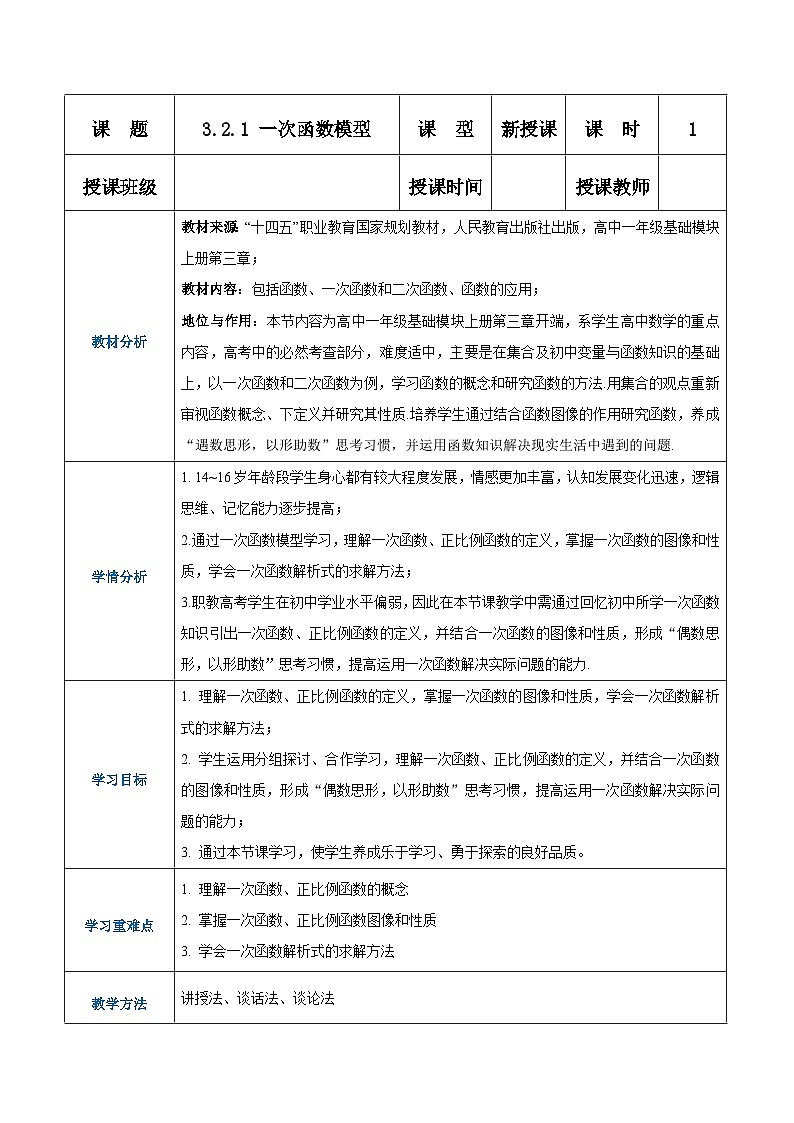
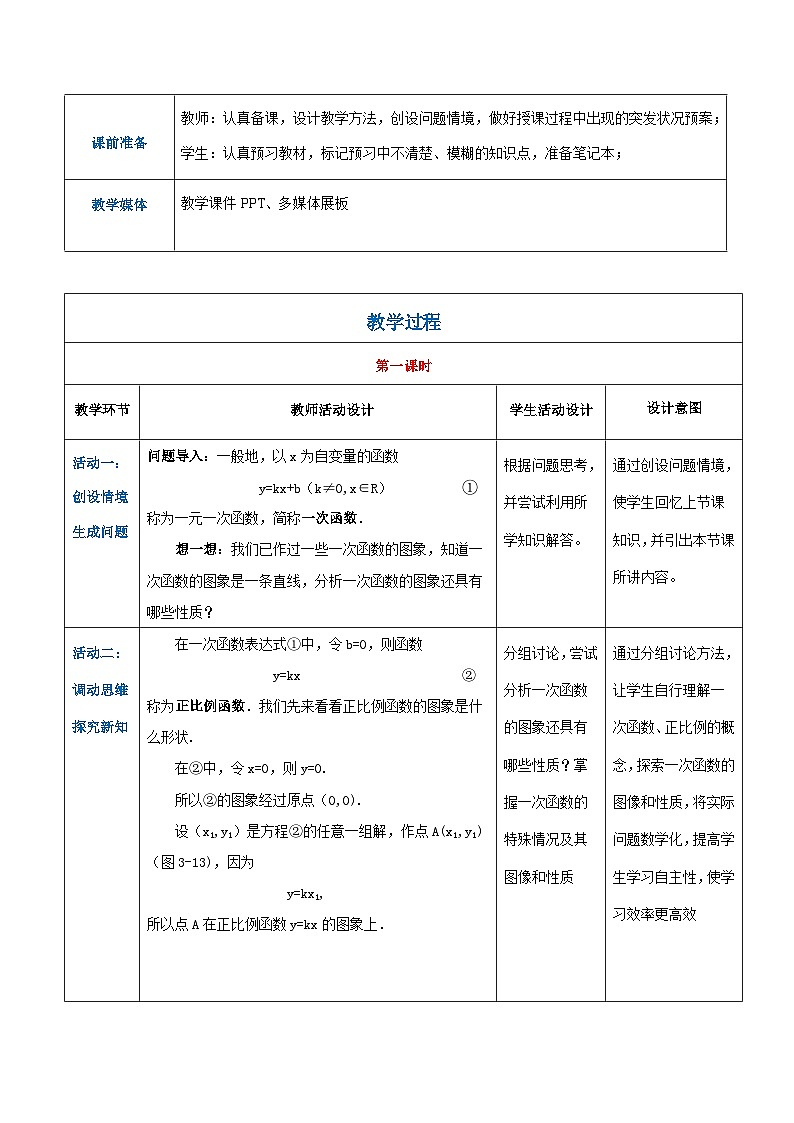
课  题3.2.1 一次函数模型课  型新授课课  时1授课班级 授课时间 授课教师 教材分析教材来源：“十四五”职业教育国家规划教材，人民教育出版社出版，高中一年级基础模块上册第三章；教材内容：包括函数、一次函数和二次函数、函数的应用；地位与作用：本节内容为高中一年级基础模块上册第三章开端，系学生高中数学的重点内容，高考中的必然考查部分，难度适中，主要是在集合及初中变量与函数知识的基础上，以一次函数和二次函数为例，学习函数的概念和研究函数的方法.用集合的观点重新审视函数概念、下定义并研究其性质.培养学生通过结合函数图像的作用研究函数，养成“遇数思形，以形助数”思考习惯，并运用函数知识解决现实生活中遇到的问题.学情分析14~16岁年龄段学生身心都有较大程度发展，情感更加丰富，认知发展变化迅速，逻辑思维、记忆能力逐步提高；2.通过一次函数模型学习，理解一次函数、正比例函数的定义，掌握一次函数的图像和性质，学会一次函数解析式的求解方法；3.职教高考学生在初中学业水平偏弱，因此在本节课教学中需通过回忆初中所学一次函数知识引出一次函数、正比例函数的定义，并结合一次函数的图像和性质，形成“偶数思形，以形助数”思考习惯，提高运用一次函数解决实际问题的能力.学习目标理解一次函数、正比例函数的定义，掌握一次函数的图像和性质，学会一次函数解析式的求解方法；学生运用分组探讨、合作学习，理解一次函数、正比例函数的定义，并结合一次函数的图像和性质，形成“偶数思形，以形助数”思考习惯，提高运用一次函数解决实际问题的能力；通过本节课学习，使学生养成乐于学习、勇于探索的良好品质。学习重难点理解一次函数、正比例函数的概念掌握一次函数、正比例函数图像和性质学会一次函数解析式的求解方法教学方法讲授法、谈话法、谈论法课前准备教师：认真备课，设计教学方法，创设问题情境，做好授课过程中出现的突发状况预案；学生：认真预习教材，标记预习中不清楚、模糊的知识点，准备笔记本；教学媒体教学课件PPT、多媒体展板   教学过程第一课时教学环节教师活动设计学生活动设计设计意图活动一：创设情境 生成问题问题导入：一般地，以x为自变量的函数
y=kx+b（k≠0,x∈R）          ①称为一元一次函数，简称一次函数．想一想：我们已作过一些一次函数的图象，知道一次函数的图象是一条直线，分析一次函数的图象还具有哪些性质？根据问题思考，并尝试利用所学知识解答。通过创设问题情境，使学生回忆上节课知识，并引出本节课所讲内容。活动二： 调动思维探究新知在一次函数表达式①中，令b=0，则函数
                 y=kx                      ②
称为正比例函数．我们先来看看正比例函数的图象是什么形状.
    在②中，令x=0，则y=0.
    所以②的图象经过原点（0,0).
    设（x1,y1）是方程②的任意一组解，作点A(x1,y1)（图3-13)，因为
                   y=kx1,
所以点A在正比例函数y=kx的图象上．            过点O和点A作直线OA.
我们来说明直线OA是一次函数y=kx的图象．
设P(x,y）为直线OA上任意一点，过点A和点P分别作x轴的垂线，垂足为M,N，则
             △OAM∽△OPN.
    由相似三角形的对应边成比例，可推出
                 .
    这说明直线OA上的所有点的坐标都满足函数关系式
                   y=kx.
    反之，如果点 P 的坐标(x,y）满足y=kx，则点P一定在直线OA上．
    综上，就可得到结论：
    函数y=kx的图象是一条过原点和点A的直线，显然函数y=kx是奇函数.
    我们再来看一般的一次函数的图象（图3-14).          从函数解析式y=kx与y=kx+b，我们可以看出，当自变量取相同的值，y=kx+b总可以由正比例函数y=kx的对应值加上b得到，这表示y=kx+b的图象是由y=kx的图象沿y轴方向平位｜b｜个单位得到．①对于一次函数y=kx+b(k≠0,x∈R)，当x=0时，y=b ；当y=0时，.所以一次函数的图象是通过点（0,b）和点的一条直线.探索研究
一次函数具有哪些主要性质？
设（x1,y1),(x2,y2）是方程①的两组解，则
           y1=kx1+b,                  ③y2=kx2+b.                   ④

④-③，整理得y2-y1=k(x2-x1).令△y=y2-y1,△x=x2-x1，则
                  △y=k△x.
    这就是说，(1）一次函数函数值的改变量与相应自变量的改变量成正比．
    (2）当k＞0时，一次函数是增函数；当k＜0时，一次函数是减函数．分组讨论，尝试分析一次函数的图象还具有哪些性质？掌握一次函数的特殊情况及其图像和性质                            注：①b＞0时，沿y轴正向平移b个单位；b＜0时，沿y轴负向平移-b个单位.通过分组讨论方法，让学生自行理解一次函数、正比例的概念，探索一次函数的图像和性质，将实际问题数学化，提高学生学习自主性，使学习效率更高效     活动三：巩固练习素质提升例.  已知点A（1,3），B（3，y）是正比例函数y=kx图像上的两点，求点B的纵坐标y.解  因为点A（1,3），B（3，y）是正比例函数y=kx图像上的两点，则3=k                 ①y=3k                ②将①式代入②式，整理得y=9.所以点B的纵坐标为y=9.分组讨论，限时完成，学生上台黑板作答，并进行讲解鼓励学生勇于展示自己，提高学生对知识的准确认识，调动学生的课堂气氛与学习的积极性，培养学生对数学的热爱，巩固学生对本节课知识的掌握，纠正学习过程中的偏差    活动四：课堂小结作业布置（一）课堂小结      （二）作业布置完成课本中P93  ——  A组1. /2.B组1./3. 活动五：板书设计 3.2.1 一次函数模型一、一次函数                                     例题                 小结   二、正比例函数                                   练习                 作业三、一次函数图像和性质活动六： 教学反思（留白）教学反思包括5个方面，教学目标、教学内容、教学实施、教学评价、教学效果。所谓教学反思，是指教师对教育教学实践的再认识、再思考，并以此来总结经验教训，进一步提高教育教学水平。教学反思一直以来是教师提高个人业务水平的一种有效手段，教育上有成就的大家一直非常重视之。