【中职专用】（高教版2021·基础模块上册）高中数学同步3.4函数的应用（同步练习）-

3.4  函数的应用

同步练习

一、选择题。

1.小明骑车上学，开始以某一速度行使，途中自行车发生了故障，修好后，小明加快了速度，准时赶到了学校，下面四个函数图像（S为路程，t为时间），能反映上述过程的是（     ）

【答案】C.

【解析】小明在途中修车时，随着时间的流逝，路程是不变的，应该是一条平行于x轴的一条线段，所以答案选C.

2.小明用一根长为8cm的铁丝围成一个矩形，则矩形的最大面积是（     ）

A.4                                           B.6 

C.8                                           D. 10

【答案】A.

【解析】设长为a，则宽为-a=4-a，矩形面积为a(4-a)=-+4a=-(a-2)2+4,因为二次函数图像开口向下有最大值，当a=2时，最大值为4.答案选A.

3.已知函数   则=（     ）

A.1                                           B.3

C.5                                           D. 4

【答案】B.

【解析】 因为0在范围内，所以=1，因为1在范围内，所以=1+2=3.即=3，所以答案选择B.

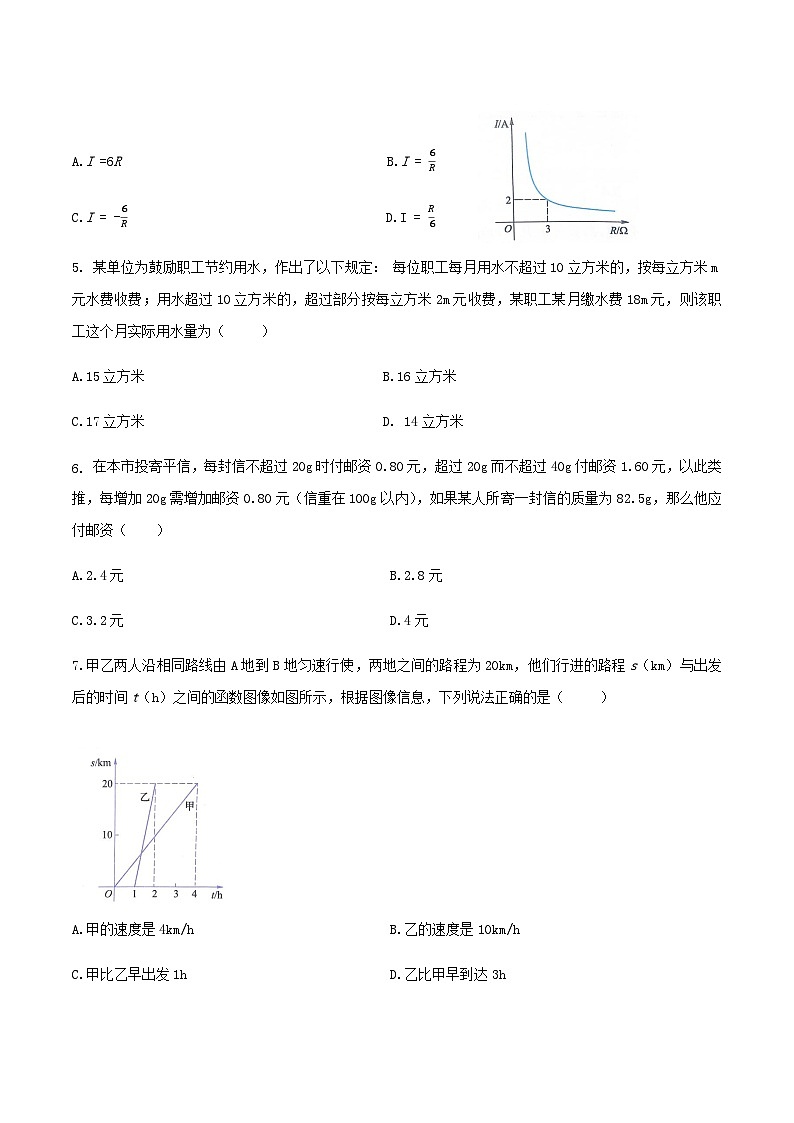
4.如图所示，某闭合电路中，若电源电压为定值，则电流I(A)与电阻R（Ω）之间呈反比例函数关系，下列关于电流I与电阻R之间的函数解析式正确的是（      ）

A.I =6R                                     B.I =

C.I = -                                     D.I =

【答案】B.

【解析】因为电流I(A)与电阻R（Ω）之间呈反比例函数关系，所以设解析式为I = ，当R=3时，I=2，

即 =2，解得m=6，所以解析式为I = .答案选择B.

5. 某单位为鼓励职工节约用水，作出了以下规定： 每位职工每月用水不超过10立方米的，按每立方米m元水费收费；用水超过10立方米的，超过部分按每立方米2m元收费，某职工某月缴水费18m元，则该职工这个月实际用水量为（     ）   

A.15立方米                                  B.16立方米   

C.17立方米                                  D. 14立方米

【答案】D.

【解析】因为用水超过10立方米的，超过部分按每立方米2m元收费，所以设用水量为x，费用为y，

则y=10m+2m（x-10），当y=18m时，解得x=14，则该职工这个月实际用水量为14立方米。答案选D.

6. 在本市投寄平信，每封信不超过20g时付邮资0.80元，超过20g而不超过40g付邮资1.60元，以此类推，每增加20g需增加邮资0.80元（信重在100g以内），如果某人所寄一封信的质量为82.5g，那么他应付邮资（    ）

A.2.4元                                      B.2.8元

C.3.2元                                      D.4元

【答案】D.

【解析】因为82.5-20=62.5g，62.5÷20=3···2.5，所以所付邮资为0.80+4×0.80=4元。答案选D.

7.甲乙两人沿相同路线由A地到B地匀速行使，两地之间的路程为20km，他们行进的路程s（km）与出发后的时间t（h）之间的函数图像如图所示，根据图像信息，下列说法正确的是（     ）

A.甲的速度是4km/h                          B.乙的速度是10km/h

C.甲比乙早出发1h                           D.乙比甲早到达3h

【答案】C.

【解析】由图像得，甲4小时行使的路程为20km，则甲的速度为5km/h，A错误；乙在甲出发1小时后才出发，1小时行使的路程为20km，则乙的速度为20km/h，乙错误;甲比乙早出发1h ，乙比甲早到达2h，D错误，C正确.

1.小明奶奶计划用长度为20m的栅栏靠墙围成一个矩形菜地，如图所示，要求菜地面积不小于42m2，假设与墙平行的矩形的边长的长度为m，请问的取值范围(单位：m）.

【解析】如图所示，设矩形长为 m，则矩形的宽度为m，

因为要求菜地面积不小于42m2，

所以列式为：

· ≥42，

解得6≤≤14，

故的取值范围为[6,14].

2.李老师在菜市场购买标价为4元/kg的土豆 （kg），并花2元钱买了一个能装6kg物品的环保购物袋，求应付款y（元）的函数解析式．

【解析】因为花2元钱买了一个能装6kg物品的环保购物袋，

所以的取值范围为≤6，

因为土豆单价为4元/kg，

所以应付款y（元）的函数解析式为：y=2+4，（≤6）.

3. 要修建一个圆形喷水池，在池中竖直安装一根水管，在水管的顶端安装一个喷水头，使喷出的抛物线水柱在与池中心的水平距离为1m处达到最高，高度为3m,水柱落地处离池中心3m,水管应多长？

【解析】由题意得，可建立平面直角坐标系（如图所示），则点（1,3）是此抛物线的顶点，

因此可设为抛物线为：y=a（x-1）2+3（0≤x≤3）

因为此抛物线过点（3,0）

所以0=a（3-1）2+3  解得a=-

所以y=-（x-1）2+3

当x=0时，y=2.25.

所以水管应长2.25m.

4.某中职学校对学生进行体育成绩测试，如图所示，某学生投掷的实心球经过的路线为y=−图像的一部分，其中图像与x轴的交点即为铅球的着陆点.

（1）铅球在运行过程中离地面的最大高度是多少米？

（2）该学生的成绩是多少米？

【解析】（1）因为求铅球在运行过程中离地面的最大高度，

就是求二次函数的最高点的纵坐标，即为 =，

所以铅球在运行过程中离地面的最大高度是米。

（2）问该学生成绩就是铅球的着陆点到原点的距离，

所以令y=0，解得x=-3（舍去）或x=7.

答：该学生的成绩为7米。

5.某品牌汽车邮箱最大容量为50L,平均耗油量为百公里10L,已知汽车邮箱中还有汽油40L,如果不再加油，那么汽车中的油量y(单位：L)随行驶里程x(单位：km)的增加而减少.

(1)写出y与x的函数关系式；

(2)汽车行驶150km,邮箱中还有多少汽油？

【解析】（1）由题意得，y与x的函数关系式为：

y=40-0.1x（0≤x≤400）

(2)    当x=150时，y=40-0.1×150=25.

        所以汽车行驶150km,邮箱中还有25L汽油.

1. 将进货单价为40元的商品按50元售出时，能卖500个，已知这种商品每涨价1元，其销售量就减少10个，为了赚取最大利润，售价应定为多少元？

【解析】解：设利润为y元，售价提高x元，售价就为（50+x）元，则由题意得

          提高价格后的每件利润为（50+x-40）元，销售量为（500-10x）件，则列式为：

                        y=（50+x-40）（500-10x）

y=-10x2+400x+5000

配方得  y=-10(x-20)2+9000

因为-10 ＜0  ，所以图像开口向下，y有最大值，

即当x=20时，y有最大值9000.

所以50+x=70

            答：为了赚取最大利润，售价应定为70元.

2. 某市出租车收费标准为：当行程不超过3km时，收费8元；当行程超过3km但不超过10km时，在收费8元的基础上，超过3km的部分按1.5元/km收费；当行程超过10km时，超过10km的部分按2元/km收费。

（1）写出车费y（元）与行程x（km）的函数关系式；

（2）若甲乘客乘车9km，则应付费用多少元钱？

（3）若乙乘客乘车12km，则应付费用多少元钱？

【解析】（1）此题函数为分段函数，第一段函数：当x≤3时，y=8；

           第二段函数：当3＜x≤10时，y=8+1.5（x-3）=3.5+1.5x；

第三段函数为：当x＞10时，y=8+1.5×（10-3）+2（x-10）=2x-1.5.

综上所述：车费y（元）与行程x（km）的函数关系式为：

y=

（2）若甲乘客乘车9km，符合第二段函数解析式，y=3.5+1.5×9=17元，

则应付费用17元钱.

（3）若乙乘客乘车12km，符合第三段函数解析式，y=2×12-1.5=22.5元，

则应付费用22.5元钱.