高中数学人教A版 (2019)选择性必修 第一册3.3 抛物线教学设计

这是一份高中数学人教A版 (2019)选择性必修 第一册3.3 抛物线教学设计，共5页。
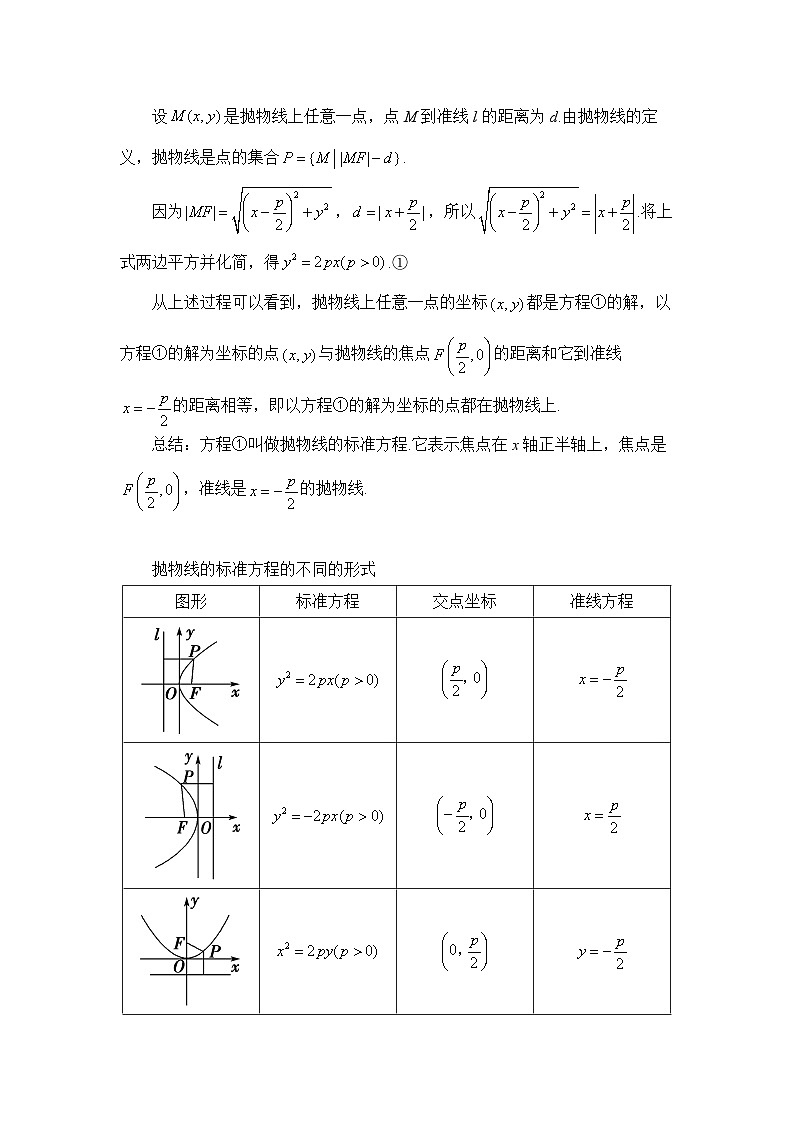
第三章 圆锥曲线的方程3.3.1 抛物线及其标准方程教学设计教学目标1.了解抛物线的定义、几何图形和标准方程.2.通过对抛物线的学习，进一步体会数形结合思想. 教学重难点教学重点：抛物线的定义、标准方程.教学难点：抛物线标准方程的推导. 教学过程新知积累1.抛物线的定义平面内与一个定点F和一条定直线l（l不经过点F）的距离相等的点的轨迹叫做抛物线. 点F叫做抛物线的焦点，直线l叫做抛物线的准线. 2.抛物线的标准方程根据抛物线的几何特征，如图，取经过点F且垂直于直线l的直线为x轴，垂足为K，并使原点与线段KF的中点重合，建立平面直角坐标系Oxy.设，那么焦点F的坐标为，准线l的方程为.设是抛物线上任意一点，点M到准线l的距离为d.由抛物线的定义，抛物线是点的集合.因为，，所以.将上式两边平方并化简，得.①从上述过程可以看到，抛物线上任意一点的坐标都是方程①的解，以方程①的解为坐标的点与抛物线的焦点的距离和它到准线的距离相等，即以方程①的解为坐标的点都在抛物线上.总结：方程①叫做抛物线的标准方程.它表示焦点在x轴正半轴上，焦点是，准线是的抛物线. 抛物线的标准方程的不同的形式图形标准方程交点坐标准线方程 例题巩固例1 （1）已知抛物线的标准方程是，求它的焦点坐标和准线方程；（2）已知拋物线的焦点是，求它的标准方程.解：（1）因为，抛物线的焦点在x轴正半轴上，所以它的焦点坐标是，准线方程是.（2）因为抛物线的焦点在轴负半轴上，且，，所以抛物线的标准方程是 例2 一种卫星接收天线如左图所示，其曲面与轴截面的交线为抛物线.在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线，经反射聚集到焦点处，如图（1）.已知接收天线的口径（直径）为4.8 m，深度为1 m.试建立适当的坐标系，求抛物线的标准方程和焦点坐标.   解：如图（2），在接收天线的轴截面所在平面内建立直角坐标系，使接收天线的顶点（即拋物线的顶点）与原点重合，焦点在轴上.设抛物线的标准方程是.由已知条件得，点的坐标是，代入方程，得，即.所以，所求抛物线的标准方程是，焦点坐标是. 课堂练习1.过焦点为F的抛物线上一点M向其准线作垂线，垂足为N，若，则(   )A. B. C. D.答案：B解析：记准线与x轴的交点为A，因为，，所以，即点M的纵坐标为8或-8，设点M的横坐标为，则，故.故选B.2.（多选）经过点的抛物线的标准方程可以为(   )A. B. C. D.答案：AD解析：点在第四象限，则抛物线的焦点可能在x轴正半轴或y轴负半轴.当拋物线的焦点在x轴正半轴时，设抛物线方程为，将点P的坐标代入，得，则抛物线的方程为；当抛物线的焦点在y轴负半轴时，设抛物线的方程为，将点P的坐标代入，得，则抛物线的方程为.故选AD.3.一个抛物线形拱桥，当水面离拱顶2 m时，水面宽8 m.若水面下降1 m，则水面宽度为____________m.答案：解析：以拱桥顶点为原点，建立平面直角坐标系，设拋物线方程.由题意知，抛物线经过点和点，代入拋物线方程，解得，所以抛物线方程为，若水面下降1 m，即，解得，，所以此时水面宽度为. 小结作业小结：本节课学习了抛物线及其标准方程.作业：完成本节课课后习题. 板书设计3.3.1 抛物线及其标准方程1.抛物线的定义2.抛物线的标准方程