2022-2023学年辽宁省沈阳市法库县九年级（上）期末数学试卷（含解析）

2022-2023学年辽宁省沈阳市法库县九年级（上）期末数学试卷

一、选择题（本大题共10小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）

1.  若方程有解，则的取值范围是(    )

A.  B.  C.  D.

2.  如图的两个几何体分别由个和个相同的小正方体搭成，比较两个几何体的三视图，正确的是(    )

A. 仅主视图不同 B. 仅俯视图不同
C. 仅左视图不同 D. 主视图、左视图和俯视图都相同

3.  如图，某停车场入口的栏杆，从水平位置绕点旋转到的位置，已知的长为米．若栏杆的旋转角，则栏杆端升高的高度为(    )
 

A. 米
B. 米
C. 米
D. 米

4.  反比例函数的图像经过点，则下列说法错误的是(    )

A.  B. 函数图像分布在第一、三象限
C. 当时，随的增大而增大 D. 当时，随的增大而减小

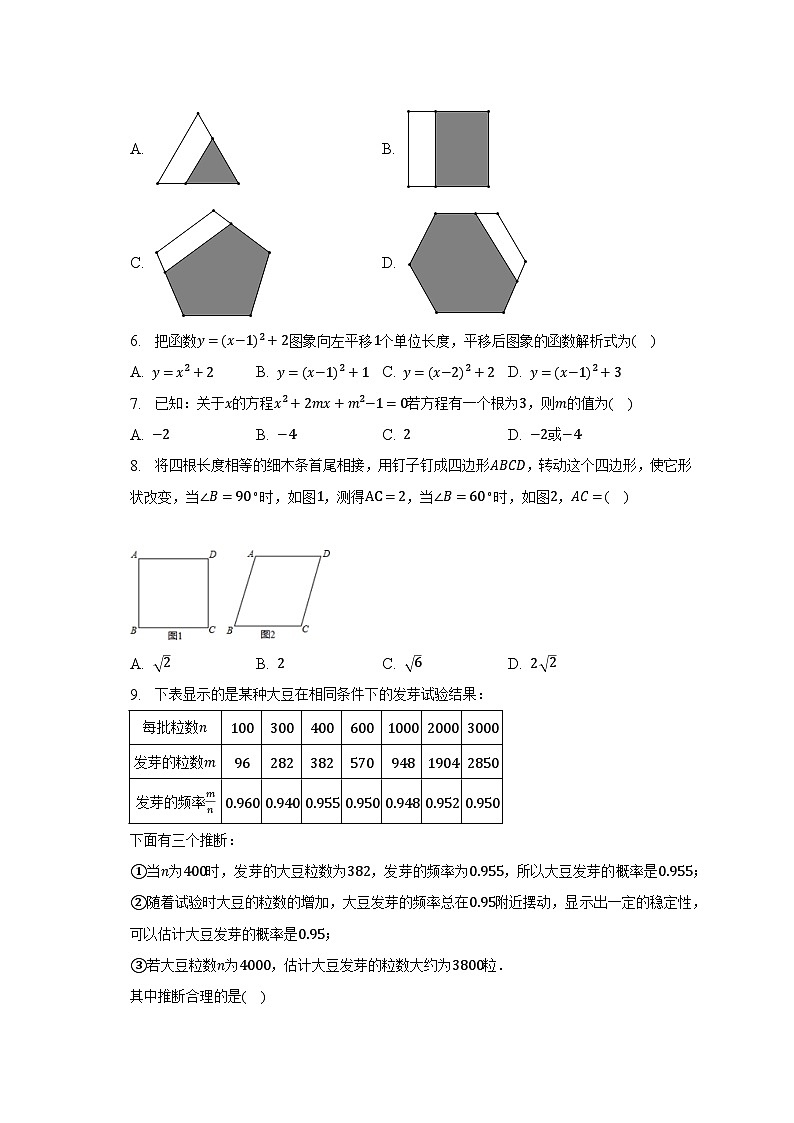
5.  如图，平行于正多边形一边的直线，正多边形分割成两部分，则阴影部分多边形与原多边形相似的是(    )

A.  B.
C.  D.

6.  把函数图象向左平移个单位长度，平移后图象的函数解析式为(    )

A.  B.  C.  D.

7.  已知：关于的方程若方程有一个根为，则的值为(    )

A.  B.  C.  D. 或

8.  将四根长度相等的细木条首尾相接，用钉子钉成四边形，转动这个四边形，使它形状改变，当时，如图，测得，当时，如图，(    )

 

A.  B.  C.  D.

9.  下表显示的是某种大豆在相同条件下的发芽试验结果：

下面有三个推断：
当为时，发芽的大豆粒数为，发芽的频率为，所以大豆发芽的概率是；
随着试验时大豆的粒数的增加，大豆发芽的频率总在附近摆动，显示出一定的稳定性，可以估计大豆发芽的概率是；
若大豆粒数为，估计大豆发芽的粒数大约为粒．
其中推断合理的是(    )

A.  B.  C.  D.

10.  已知抛物线过、两点，则下列关系式一定正确的是(    )

A.  B.  C.  D.

二、填空题（本大题共6小题，共18.0分）

11.  抛物线的顶点坐标是______．

12.  年是中国共产党建党周年，全国各地积极开展“弘扬红色文化，重走长征路”主题教育活动．据了解，某展览中心月份的参观人数为万人，月份的参观人数增加到万人．设参观人数的月平均增长率为，则可列方程为          ．

13.  如图的方格地面上，标有编号，，的个小方格地面是空地，另外个小方格地面是草坪，除此以外小方格地面完全相同，一只自由飞行的鸟，将随意地落在图中的方格地面上，则小鸟落在草坪上的概率是______ ．

14.  如图，在边长为的菱形中，点在边上，点为的延长线与的延长线的交点，若，则的长为______ ．

15.  如图，在平面直角坐标系中，点为此标原点，平行四边形的顶点在反比例函数的图象上，顶点在反比例函数的图象上，顶点在轴的负半轴上，若平行四边形的面积是，则的值是______ ．

16.  如图，矩形纸片，，，为边上一点．将沿所在的直线折叠，点恰好落在边上的点处，过点作，垂足为点，取的中点，连接，则______．

三、计算题（本大题共1小题，共6.0分）

17.  计算：．

四、解答题（本大题共8小题，共76.0分。解答应写出文字说明，证明过程或演算步骤）

18.  本小题分
第十五届中国“西博会”将于年月底在成都召开，现有名志愿者准备参加某分会场的工作，其中男生人，女生人．
若从这人中随机选取一人作为联络员，求选到女生的概率；
若该分会场的某项工作只在甲、乙两人中选一人，他们准备以游戏的方式决定由谁参加，游戏规则如下：将四张牌面数字分别为，，，的扑克牌洗匀后，数字朝下放于桌面，从中任取张，若牌面数字之和为偶数，则甲参加，否则乙参加．试问这个游戏公平吗？请用树状图或列表法说明理由．

19.  本小题分
如图，在▱中，，，垂足分别为，．
求证：≌；
求证：四边形为矩形．

20.  本小题分
某无人机兴趣小组在操场上开展活动如图，此时无人机在离地面米的处，无人机测得操控者的俯角为，测得点处的俯角为又经过人工测量操控者和教学楼距离为米，求教学楼的高度．注：点，，，都在同一平面上．参考数据：，，

21.  本小题分
如图，在平面直角坐标系中，一次函数为常数，且与反比例函数为常数，且的图象交于点，．
求反比例函数和一次函数的表达式．
当时，直接写出自变量的取值范围．

22.  本小题分
如图，在中，点，，分别在，，边上，，．
求证：∽．
设，
若，求线段的长；
若的面积是，求的面积．

23.  本小题分
小李在景区销售一种旅游纪念品，已知每件进价为元，当销售单价定为元时，每天可以销售件，市场调查反映：销售单价每提高元，日销量将会减少件，物价部门规定：销售单价不能超过元，设该纪念品的销售单价为元，日销量为件，日销售利润为元．
求与的函数关系式；
求日销售利润元与销售单价元的函数关系式，当为何值时，日销售利润最大，并求出最大利润．

24.  本小题分
正方形中，点是边上的任意一点，连接，为的中点，作于，连接，．
若，求的大小用含的式子表示；
若，求长．

25.  本小题分
已知抛物线与轴交于，两点，与轴交于点，点是抛物线上在第一象限内的一个动点，且点的横坐标为．
求抛物线的表达式；
如图，连接，，，设的面积为．
求关于的函数表达式；
求点到直线的距离的最大值，并求出此时点的坐标．
如图，设抛物线的对称轴为，与轴的交点为，在直线上是否存在点，使得四边形是平行四边形？若存在，直接写出点的坐标；若不存在，请说明理由．

答案和解析

1.【答案】 

【解析】解：根据题意得时，方程有实数解．
故选：．
利用平方根的定义确定的范围．
本题考查了解一元二次方程直接开平方法：形如或的一元二次方程可采用直接开平方的方法解一元二次方程．
 

2.【答案】 

【解析】解：从正面看，两个几何体均为第一层和第二层都是两个小正方形，故主视图相同；
从左面看，两个几何体均为第一层和第二层都是两个小正方形，故左视图相同；
从上面看，两个几何体均为第一层和第二层都是两个小正方形，故俯视图相同．
故选：．
根据主视图是从物体的正面看得到的视图，俯视图是从上面看得到的图形，左视图是左边看得到的图形，可得答案．
本题考查了简单组合体的三视图，利用三视图的意义是解题关键．
 

3.【答案】 

【解析】解：过点作于点，

由题意可知：，
，
，
故选：．
过点作于点，根据锐角三角函数的定义即可求出答案．
本题考查解直角三角形的应用，解题的关键是熟练运用锐角三角函数的定义，本题属于基础题型．
 

4.【答案】 

【解析】解：反比例函数的图像经过点，
．
．
故A正确；
，
双曲线分布在第一、三象限，
故B选项正确；
当时，反比例函数在每一个象限内随的增大而减小，
即当或时，随的增大而减小．
故C选项错误，选项正确，
综上，说法错误的是，
故选：．
利用待定系数法求得的值，再利用反比例函数图象的性质对每个选项进行逐一判断即可．
本题主要考查了反比例函数图象上点的坐标的特征，待定系数法确定函数的解析式，反比例函数图象的性质．利用待定系数法求得的值是解题的关键．
 

5.【答案】 

【解析】

【分析】
本题考查的是相似多边形的判定，解题的关键是理解对应角相等，对应边的比相等的多边形是相似多边形．根据相似多边形的判定判定定理判断即可．
【解答】
解：、阴影三角形与原三角形的对应角相等、对应边的比相等，符合相似多边形的定义，符合题意；
B、阴影矩形与原矩形的对应角相等，但对应边的比不相等，不符合相似多边形的定义，不符合题意；
C、阴影五边形与原五边形的对应角相等，但对应边的比不相等，不符合相似多边形的定义，不符合题意；
D、阴影六边形与原六边形的对应角相等，但对应边的比不相等，不符合相似多边形的定义，不符合题意；
故选：．  

6.【答案】 

【解析】解：原抛物线的顶点为，
向左平移个单位后，得到平移后抛物线的顶点为，
平移后图象的函数解析式为：．
故选：．
易得原抛物线的顶点为，根据相应的平移得到新抛物线的顶点，利用平移不改变二次项的系数，利用顶点式解析式可得新抛物线解析式．
本题考查了二次函数图象与几何变换：先把二次函数的解析式配成顶点式，然后把抛物线的平移问题转化为顶点的平移问题．
 

7.【答案】 

【解析】解：已知关于的方程有一个根为，则：
，
整理得，
解得，，
故选：．
将代入方程中即可求出的值．
此题重点考查学生对一元二次方程解的理解，掌握一元二次方程的解法是解题的关键．
 

8.【答案】 

【解析】

【分析】
本题考查了正方形的性质，勾股定理以及等边三角形的判定和性质，利用勾股定理得出正方形的边长是关键．图中根据勾股定理即可求得正方形的边长，图根据有一个角是的等腰三角形是等边三角形即可求得．
【解答】
解：如图，
，，
四边形是正方形，
连接，则，
，

如图，，连接，，
为等边三角形，
．
故选A．  

9.【答案】 

【解析】解：当时，发芽的大豆粒数为，发芽的频率为，但概率大约是，故此推断不合理；
根据上表当每批粒数足够大时，频率逐渐接近于，所以估计大豆发芽的概率是，故此推断合理；
若为，估计大豆发芽的粒数大约为粒，故此推断合理，
综上可知，推断合理的是．
故选：．
根据表中信息，当每批粒数足够大时，频率逐渐接近于，由于试验次数较多，可以用频率估计概率．
本题主要考查利用频率估计概率，大量反复试验下频率稳定值即为概率．
 

10.【答案】 

【解析】解：抛物线，
关于轴对称点的坐标为，
，
时，随的增大而减小，
，
；
故选：．
依据抛物线的对称性可知：在抛物线上，然后依据二次函数的性质解答即可．
本题主要考查的是二次函数的性质，熟练掌握二次函数的对称性和增减性是解题的关键．
 

11.【答案】 

【解析】

【分析】
本题考查了二次函数的性质，形如的顶点坐标为，据此可以直接求出顶点坐标．
【解答】
解：抛物线的顶点坐标为．
故答案是：．  

12.【答案】 

【解析】解：依题意得：．
故答案为：．
利用月份的参观人数月份的参观人数月平均增长率，即可得出关于的一元二次方程，此题得解．
本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
 

13.【答案】 

【解析】解：小鸟落在草坪上的概率．
故答案为：．
据图直接由概率公式求解即可．
本题考查了概率公式的简单运用，解题的关键是熟练掌握概率所求情况数与总情况数之比．
 

14.【答案】 

【解析】解：四边形是边长为的菱形，，
，，
∽，
，即，
．
故答案为：．
根据菱形的性质可得出，进而可得出∽，由、的长度可求出的长度，再利用相似三角形的性质即可求出的长度．
本题考查了相似三角形的判定与性质以及菱形的性质，利用相似三角形的性质找出与之间的关系是解题的关键．
 

15.【答案】 

【解析】解：设，
四边形是平行四边形，
，
，
，
平行四边形的面积是，
，
解得，
故答案为：．
设，根据四边形是平行四边形，推出，表示出点的坐标，求出，再根据平行四边形面积公式列方程，解出即可．
本题考查反比例函数比例系数的几何意义、反比例函数图象上点的坐标特征、平行四边形性质，掌握反比例函数比例系数的几何意义及函数图象上点的坐标特征，设出点的坐标、根据平行四边形面积公式列方程是解题的关键．
 

16.【答案】 

【解析】解：连接，．

由翻折的性质可知，垂直平分线段，
，
，，共线，，
，
，
四边形是矩形，
，
，
，
故答案为．
连接，，求出，利用三角形的中位线定理解决问题即可．
本题考查翻折变换，矩形的性质，三角形的中位线定理等知识，解题的关键是学会添加常用辅助线，构造三角形中位线解决问题，属于中考常考题型．
 

17.【答案】解：原式

． 

【解析】本题考查了实数的运算、零指数幂、负整数指数幂、特殊角的三角函数值，解决本题的关键是掌握特殊角的三角函数值．根据零指数幂、负整数指数幂、特殊角的三角函数值进行计算即可求解．
 

18.【答案】解：现有名志愿者准备参加某分会场的工作，其中男生人，女生人，
从这人中随机选取一人作为联络员，选到女生的概率为：；

如图所示：

牌面数字之和为：，，，，，，，，，，，，
偶数为：个，得到偶数的概率为：，
得到奇数的概率为：，
甲参加的概率乙参加的概率，
这个游戏不公平． 

【解析】直接利用概率公式求出即可；
利用树状图表示出所有可能进而利用概率公式求出即可．
此题主要考查了游戏公平性以及概率公式应用，正确画出树状图是解题关键．
 

19.【答案】证明：，，
，
四边形为平行四边形，
，，
在和中，
，
≌；
四边形为平行四边形，
，
，
，
，
，
则四边形为矩形． 

【解析】由与垂直，与垂直，得到一对直角相等，再由为平行四边形得到，对角相等，利用即可得出结论；
由平行四边形的对边平行得到与平行，得到为直角，利用三个角为直角的四边形为矩形即可得出结论．
此题考查了矩形的判定，全等三角形的判定与性质，以及平行四边形的性质，熟练掌握矩形的判定方法是解本题的关键．
 

20.【答案】解：过点作于点，过点作于点．

由题意得，，，，．
在中，，
．

，

四边形是矩形，
．
在中，，
．


答：教学楼高约米． 

【解析】作于点，作于点，由求得，由知，再根据四边形是矩形知由知，从而得．
此题主要考查了解直角三角形的应用，利用数形结合以及锐角三角函数关系求解是解题关键．
 

21.【答案】解：由题意，得点在反比例函数图象上，
，，
反比例函数表达式为，
又点也在反比例函数图象上，
，
点，在一次函数图象上，
，
解得，
一次函数表达式为．
由图象可得，由时，自变量的取值范围． 

【解析】将坐标代入反比例函数解析式中求出的值，即可确定出反比例函数解析式；将坐标代入反比例解析式中求出的值，确定出坐标，将与坐标代入一次函数解析式中求出与的值，即可确定出一次函数解析式；
由图象直接可得自变量的取值范围．
本题属于反比例函数与一次函数的交点问题，涉及的知识有：待定系数法求函数解析式，利用了数形结合的思想，熟练掌握待定系数是解本题的关键．
 

22.【答案】解：证明：，
．
，
，
∽；
，
．
，
，
解得：；
，
．
，
∽，
，
． 

【解析】本题考查了相似三角形的判定与性质、平行线的性质等知识；熟练掌握相似三角形的判定与性质是解题的关键．
由平行线的性质得出，，即可得出结论；
由平行线分线段成比例得出，即可得出结果；
先求出，易证∽，由相似三角形的面积比等于相似比的平方即可得出结果．
 

23.【答案】解：根据题意得，，
故与的函数关系式为；
根据题意得，，
，
当时，随的增大而增大，
当时，，
答：当为时，日销售利润最大，最大利润元． 

【解析】根据题意得到函数解析式；
根据题意得到，根据二次函数的性质即可得到结论．
此题考查了一元二次方程和二次函数的运用，利用总利润单个利润销售数量建立函数关系式，进一步利用性质的解决问题，解答时求出二次函数的解析式是关键．
 

24.【答案】解：在正方形中，，，
，
，
，
，且为的中点，
，
，
；
连接，，

在正方形中，，，，
≌，
，
在中，为的中点，
，
，
，
由知，
，
又由知，
．
是等腰直角三角形，
，
，即，
． 

【解析】根据正方形的性质得出，再根据直角三角形斜边上的中线等于斜边一半，得出，则，最后根据三角形的外角定理即可得出结论；
连接，，通过证明≌，得出，根据直角三角形斜边中线等于斜边一半，得出，则，进而得出，根据等腰直角三角形那个的性质得出，即，即可求解．
本题主要考查了正方形的性质，三角形外角定理，等腰三角形的性质，三角形全等的判定和性质，解题的关键是掌握三角形外角等于与它不相邻两个内角之和，等腰三角形“等边对等角”，直角三角形斜边上的中线等于斜边一半，以及三角形全等的判定方法．
 

25.【答案】解：将，代入，
得，
解得：，
抛物线的表达式为；
在图中，过点作轴，交于点．

设直线的解析式为，
将、代入，
，
解得：，
直线的解析式为．
点的坐标为，
点的坐标为，
，
；
，
，
当时，取最大值，最大值为．
、，
线段，
点到直线的距离的最大值为，
当时，，则此时点的坐标为；
在直线上存在点，使得四边形是平行四边形，理由如下：
如图，连接，交抛物线对称轴于点，

抛物线与轴交于，两点，
抛物线的对称轴为直线，
，
，
，
，
在中，当时，，
，
，
，
，
点的坐标为；
当时，不存在，理由如下，
若四边形是平行四边形，则，
点的横坐标为，点的横坐标为，
点的横坐标，
又，
不存在，
综上所述，在直线上存在点，使得四边形是平行四边形，点的坐标为． 

【解析】待定系数法求解析式即可求解；
在图中，过点作轴，交于点，求得直线的解析式为点的坐标为，则点的坐标为，根据三角形的面积公式得出；
根据二次函数的性质得出当时，取最大值，最大值为勾股定理求得，等面积法求得点到直线的距离，进而得出的坐标；
如图，连接，交抛物线对称轴于点，因为抛物线与轴交于，两点，所以抛物线的对称轴为直线，由平行四边形的性质及平移规律可求出点的坐标；当时，不存在．
本题考查了待定系数法求解析式，函数的思想求极值，平行四边形的存在性等，解题关键是能够灵活运用平行四边形的性质及判定等．