中考数学总复习第四章第18课时全等三角形课件

这是一份中考数学总复习第四章第18课时全等三角形课件，共40页。PPT课件主要包含了AAS，ASA，答案相等，对应的中线，对应的角平，答案题设，真命题，假命题，全等三角形的性质，A72°等内容，欢迎下载使用。

1.理解全等三角形的概念.
2.掌握两个三角形全等的判定方法.
3.了解定义、命题、定理的含义，会区分命题的条件(题设)和结论.了解逆命题的概念，会识别两个互逆命题，并知道原命题成立，其逆命题不一定成立.
1.________________的两个三角形叫作全等三角形.答案：能够完全重合2.三角形全等的判定方法有：________、______、________、________.直角三角形全等的判定除以上的方法还有 HL.
答案：SSS SAS
3.全等三角形的性质：全等三角形对应边_______，对应角________.
4.全等三角形的面积________，周长________，对应的高、____________、________________相等.
5.命题由________和________组成，命题分为________和________.
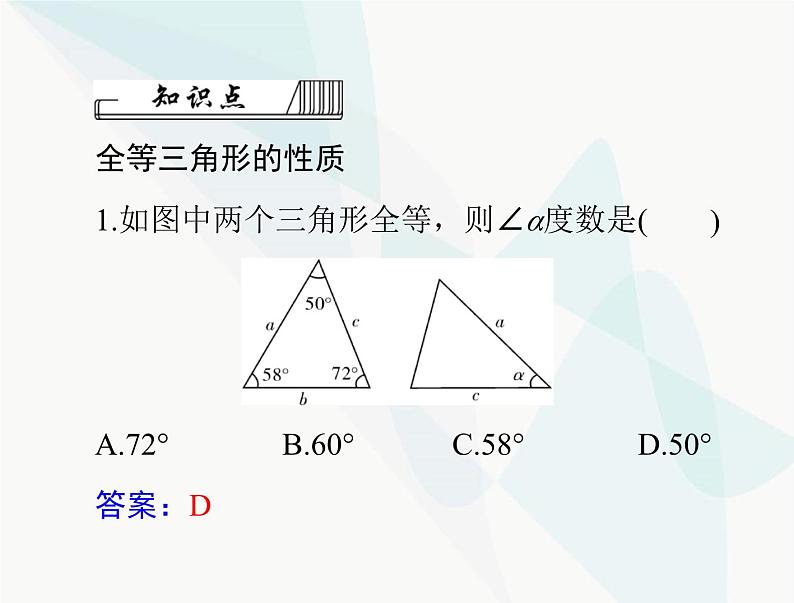
1.如图中两个三角形全等，则∠α度数是(
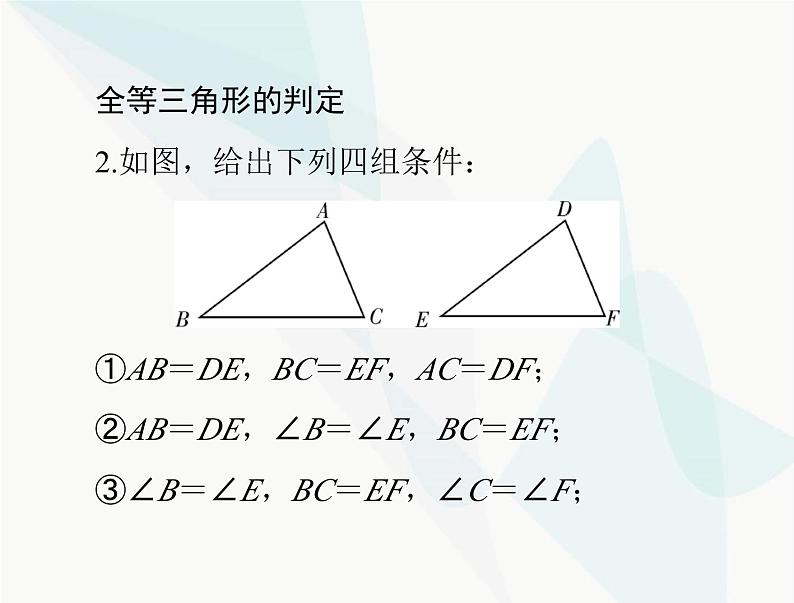
2.如图，给出下列四组条件：
①AB＝DE，BC＝EF，AC＝DF；②AB＝DE，∠B＝∠E，BC＝EF；③∠B＝∠E，BC＝EF，∠C＝∠F；
④AB＝DE，AC＝DF，∠B＝∠E.其中，能使△ABC≌△DEF 的条件有
________________.
3.(2022·广东)如图所示，已知∠AOC＝∠BOC，点 P 在 OC 上，PD⊥OA，PE⊥OB，垂足分别为 D，E.求证：△OPD≌△OPE.
证明：∵PD⊥OA，PE⊥OB，∴∠ODP＝∠OEP＝90°.∵∠AOC＝∠BOC，∴∠DOP＝∠EOP，
在△OPD 和△OPE 中，
∴△OPD≌△OPE(AAS).
命题与逆命题4.命题“等角的补角相等”的题设是________________________，结论是__________________，它的逆命题是__________________________________.
如果两个角的补角相等，那么这两个角相等
1.运用全等三角形的判定和性质，若题中没给图形，建议根据题意画出符合题意的图形，数形结合进行分析.
2.对于三角形全等的性质及判定的问题，由于已知条件的不确定或开放性问题，常用到分类讨论思想.
3.三角形全等是证明线段相等、角相等最常用的方法.证明线段(或角)相等往往转化为证明线段(或角)所在的两个三角形全等.
1.如图，已知△ABC的六个元素，则甲、乙、丙
三个三角形中和△ABC 全等的图形的是(
A.甲和乙C.只有乙答案：B
2.(2022·金华)如图所示，AC 与 BD 相交于点 O，OA＝OD，OB＝OC，不添加辅助线，判定
△ABO≌△DCO 的依据是(
3.如图，AB＝AD，AE 平分∠BAD，则图中全等三
4.工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图，在∠AOB 的两边 OA，OB 上分别截取 OC＝OD，移动角尺，使角尺两边相同的刻度分别与点 C，D 重合，这时过角尺顶点 M 的射线 OM 就是∠AOB 的平分线.这里
构造全等三角形的依据是(
5.如图，梯形 ABCD 中，AD∥BC，点 M 是 AD 的中点，且 MB＝MC，若 AD＝4，AB＝6，BC＝8，则梯
形 ABCD 的周长为(
6.(2021·哈尔滨)如图，△ABC≌△DEC，点 A 和点D 是对应顶点，点 B 和点 E 是对应顶点，过点 A 作AF⊥CD，垂足为点 F，若∠BCE＝65°，则∠CAF 的
7.(2022·南通)如图，点 B，F，C，E 在一条直线上，AB∥ED，AC∥FD，要使△ABC≌△DEF，只需添加一个条件，则这个条件可以是___________.
答案：AB＝DE(答案不唯一)
8.如图，在△ABC中，若∠1＝∠2，BE＝CD，
AB＝5，AE＝2，则 CE＝________.
9.(2022·株洲)如图所示，点 O 在一块直角三角板ABC 上(其中∠ABC＝30°)，OM⊥AB 于点 M，ON⊥BC 于点 N，若 OM＝ON，则∠ABO＝________度.
10.如图，在四边形 ABCD 中，AB＝AD，CB＝CD，对角线 AC，BD 相交于点 O，下列结论中：①∠ABC＝∠ADC；②AC 与 BD 相互平分；③AC，BD 分别平分四边形 ABCD 的两组对角；
正确的是__________.(填写所有正确结论的序号)答案：①④
11.(2022·广州)如图所示，点 D，E 在△ABC 的边BC 上，∠B＝∠C，BD＝CE，求证：△ABD≌△ACE.
证明：∵∠B＝∠C，∴AB＝AC，
在△ABD 和△ACE 中，
∴△ABD≌△ACE(SAS).
12.(2021·百色)如图，点 D，E 分别是 AB，AC 的中点，BE，CD 相交于点 O，∠B＝∠C，BD＝CE.
求证：(1)OD＝OE；(2)△ABE≌△ACD.
证明：(1)在△BOD 和△COE 中，
∴△BOD≌△COE(AAS)，∴OD＝OE.
13.如图，四边形 ACDF 是正方形，∠CEA 和∠ABF都是直角，且点 E，A，B 三点共线，AB＝4，求阴影部分△ABC 的面积.
解：∵四边形 ACDF 是正方形，
∴∠CAE＋∠FAB ＝90°.∵∠CEA＝90°，
∴∠CAE＋∠ACE＝90°，∴∠ACE＝∠FAB .又∵∠AEC＝∠FBA＝90°，∴△AEC≌△FBA(AAS)，∴CE＝AB＝4，
14.(2021·广州)如图，点 E，F 在线段 BC 上，AB∥CD，∠A＝∠D，BE＝CF，证明：AE＝DF.
证明：∵AB∥CD，∴∠B＝∠C.
∴△ABE≌△DCF(AAS).∴AE＝DF.
15.(2021·湘潭)如图，矩形 ABCD 中，E 为边 BC上一点，将△ABE 沿 AE 翻折后，点 B 恰好落在对角线 AC 的中点 F 上.
(1)证明：△AEF≌△CEF；
(2)若 AB＝ 　 ，求折痕 AE 的长度.
(1)证明：∵四边形 ABCD 是矩形，∴∠B＝90°.
∵将△ABE 沿 AE 翻折后，点 B 恰好落在对角线
AC 的中点 F 上，
∴∠AFE＝∠B＝90°，AF＝CF.∵∠AFE＋∠CFE＝180°，
∴∠CFE＝180°－∠AFE＝90°.
∴△AEF≌△CEF(SAS).
(2)解：由(1)知，△AEF≌△CEF，∴∠EAF＝∠ECF，
由折叠性质，得∠BAE＝∠EAF，∴∠BAE＝∠EAF＝∠ECF.∵∠B＝90°，
∴∠BAC＋∠BCA＝90°，
∴3∠BAE＝90°，∴∠BAE＝30°，
16.如图，AB 是⊙O 的直径，点 C 为　 的中点，CF 为⊙O 的弦，且 CF⊥AB，垂足为 E，连接 BD 交CF 于点 G，连接 CD，AD，BF.
(1)求证：△BFG≌△CDG；(2)若 AD＝BE＝2，求 BF 的长.
(2)解：如图，连接 OF，设⊙O 的半径为 r，在 Rt△ADB 中，BD2＝AB2－AD2，即 BD2＝(2r)2－22.在 Rt△OEF 中，OF2＝OE2＋EF2，即 EF2＝r2－(r－2)2.