中考数学总复习第四章第20课时解直角三角形课件

这是一份中考数学总复习第四章第20课时解直角三角形课件，共38页。PPT课件主要包含了答案90°，答案对边，短无关，答案大小，特殊角三角函数值，则α的度数，A30°，B45°，C60°，D75°等内容，欢迎下载使用。

1.理解直角三角形的概念，掌握直角三角形的性
质，掌握判断三角形是直角三角形的方法．
2.掌握勾股定理，会运用勾股定理解决简单问题，
会用勾股定理的逆定理判定直角三角形.
3.通过实例认识锐角三角函数，知道特殊角的三角函数值，由已知锐角求它的三角函数值，由已知三角函数值求它对应的锐角.
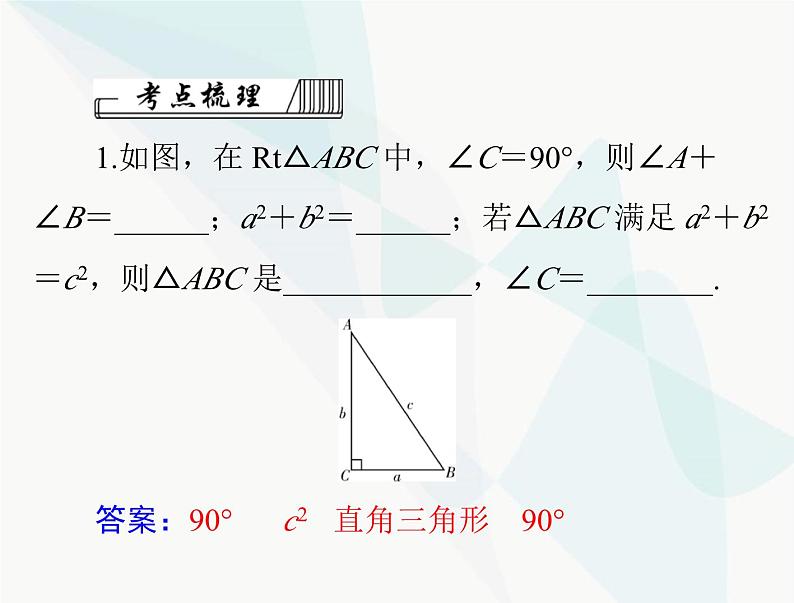
1.如图，在 Rt△ABC 中，∠C＝90°，则∠A＋∠B＝______；a2＋b2＝______；若△ABC 满足 a2＋b2＝c2，则△ABC 是____________，∠C＝________.
c2 直角三角形　90°
2.在 Rt△ABC 中，∠C＝90°，则
3.锐角三角函数值只与角的______有关，与边的长
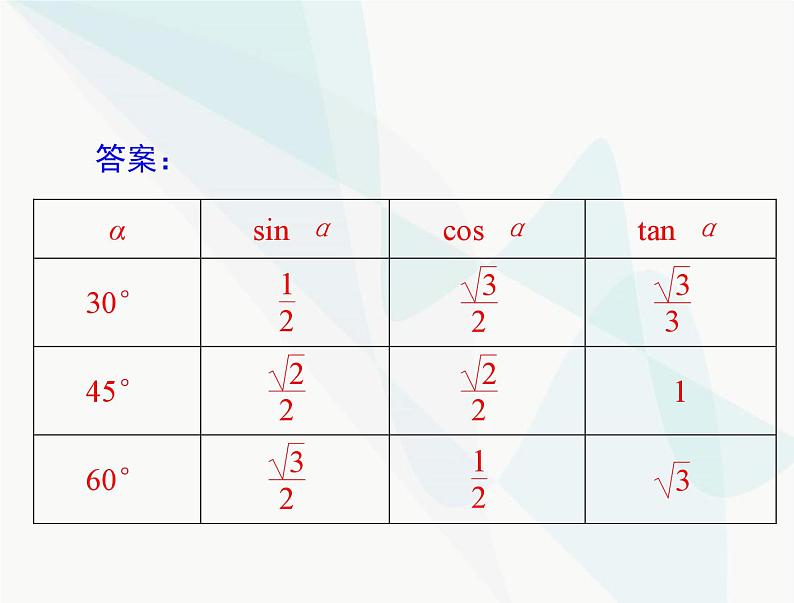
4.在下表中，填入特殊角的三角函数值.
5.在 Rt△ABC 中，若∠C＝90°，∠A＝30°，则BC＝________.
勾股定理1.(1)在 Rt△ABC 中，∠C＝90°，若 a＝8，b＝6，
(2)△ABC中，若a＝5，b＝12，c＝13，则△ABC为______角三角形.
答案：(1) a2＋b2　82＋62　10　(2)直
锐角三角函数2.在 Rt△ABC 中，∠C＝90°，AC＝3，BC＝4，则 AB＝________，sin A＝________，cs A＝_______，tan A＝________，sin B＝________，cs B＝_______，tan B＝________.
3.已知α为锐角，sin (α－15°)＝
4.如图，在 Rt△ABC 中，∠BAC＝90°，点 D 在BC边上，且△ABD是等边三角形.若AB＝2，求△ABC的周长(结果保留根号).
解：∵△ABD 是等边三角形，∴∠B＝60°.∵∠BAC＝90°，∴∠C＝180°－90°－60°＝30°，∴BC＝2AB＝4，在 Rt△ABC 中，由勾股定理，得
1.掌握锐角三角函数的关键是要熟练掌握好边角
之间的关系，注意数形结合.
2.由 15°，75°，105°等可构造特殊角，从而可
用特殊角的三角函数促使边角转化.
3.适当添加辅助线，构造直角三角形，是解答解
直角三角形问题的关键.
1.(2022·天津)tan 45°的值等于(
2.如图，以 O 为圆心，半径为 1 的弧交坐标轴于A，B 两点，P 是 　 上一点(不与 A，B 重合)，连接 OP，
)B.(cs α，cs α)D.(sin α，cs α)
设∠POB＝α，则点 P 的坐标是(A.(sin α，sin α)C.(cs α，sin α)答案：C
4.(2021·滨州)在 Rt△ABC 中，若∠C＝90°，AC
＝3，BC＝4，则点 C 到直线 AB 的距离为(
5.计算 6tan 45°－2cs 60°的结果是(
6.(2022·广州期中)如图，△ABC 的顶点在正方形
网格的格点处，则 tan C 的值为(
答案：B7.(2022·广东)sin 30°＝________.
8.(2021·广州)如图，在 Rt△ABC 中，∠C＝90°，∠A＝30°，线段 AB 的垂直平分线分别交 AC，AB 于点 D，E，连接 BD.若 CD＝1，则 AD 的长为______.
9.(2020·菏泽)如图，在△ABC 中，∠ACB＝90°，点 D 为 AB 边的中点，连接 CD，若 BC＝4，CD＝3，则 cs∠DCB 的值为________.
11.(2021·深圳)如图，已知∠BAC＝60°，AD 是角平分线且 AD＝10，作 AD 的垂直平分线交 AC 于点F，作 DE⊥AC，则△DEF 的周长为__________.
12.(2020·深圳)如图，已知四边形 ABCD，AC 与BD 相交于点 O，∠ABC＝∠DAC＝90°，tan∠ACB＝
13.(2022·湖州)如图所示，已知在 Rt△ABC 中，
∠C＝90°，AB＝5，BC＝3.求 AC 的长和 sin A 的值.
14.(2021·广东)如图所示，在 Rt△ABC 中，∠A＝90°，作 BC 的垂直平分线交 AC 于点 D，延长 AC 至点 E，使 CE＝AB.(1)若 AE＝1，求△ABD 的周长；
BD，求 tan∠ABC 的值.
解：(1)如图，连接 BD，设 BC 垂直平分线交 BC
C△ABD＝AB＋AD＋BD
＝AB＋AD＋DC＝AB＋AC，∵AB＝CE，
∴C△ABD＝AC＋CE＝AE＝1，故△ABD 的周长为 1.
(2)设 AD＝x，∴BD＝3x，又∵BD＝CD，∴AC＝AD＋CD＝4x，
sin α＋cs α.
(1)计算 sin 75°；
(2)如图，△ABC 中，AB＝1，∠ACB＝45°，∠CAB＝α，请利用这个图形证明上述结论.
(2)如图，作 AD⊥CB 交 CB 的延长线于点 D，∵AB＝1，∠ACB＝45°，∠CAB＝α，∴∠ABD＝∠ACB＋∠ACB＝45°＋α，
AC 于点 D，连接 AP.(1)求 AC，BC 的长；(2)设 PC 的长为 x，△ADP 的面积为 y.当 x 为何值时，y 最大，并求出最大值.
∴AC＝2，根据勾股定理，得 BC＝4.
(2)∵PD∥AB，∴△ABC∽△DPC，