






人教B版 (2019)必修 第二册4.6 函数的应用(二)教案配套课件ppt
展开我们已经学习了哪些具体函数?它们之间有什么联系?我们是按照什么思路研究这些函数的?
我们学习了指数函数、对数函数、幂函数,它们都与指数运算有关. 我们按照研究一类函数的定义、性质和图像的思路来研究具体函数.
这些函数在实际生活中有什么应用呢?
例1 有些银行存款是按复利的方式计算利息的,即把上一期的利息与本金加在一起作为本金,再计算下一期的利息. 本息和与哪些量有关?
你能建立本息和与存期之间的函数关系吗?至少经过多少期后本息和才能不小于本金的2倍?
本息和与最开始的本金、每期的利率及存期有关.
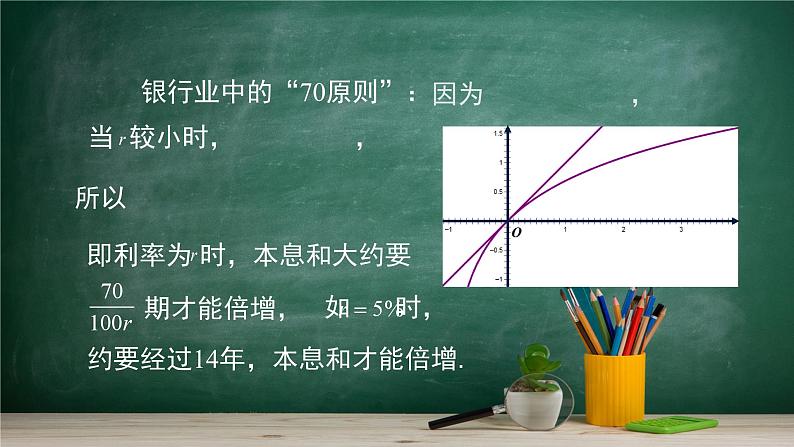
约要经过14年,本息和才能倍增.
银行业中的“70原则”:
例2 按照《国务院关于印发“十三五”节能减排综合工作方案的通知》(国发[2016]74号)的要求,到2020年,全国二氧化硫排放总量要控制在1580万吨以内,要比2015年下降15%. 假设“十三五”期间每一年二氧化硫排放总量下降的百分比都相等,2015年后第
(1)求 的解析式;(2)求2019年全国二氧化硫排放总量要控制在多少万吨以内(精确到1万吨).
可知 2019年全国二氧化硫排放总量要控制在1632万吨以内.
例3 已知某地区第一年的经济增长率为 ( 且 为常数),第二年的经济增长率为 ( ),这两年的平均经济增长率为 ,写出 与 的关系,并求 的最小值.
解:由题意,
利用函数的单调性,求函数最值.
你能总结出与增长率有关的指数模型的一般形式吗?
其中a是初值,r是增长率,x表示时间,y是终值.
例4 人们通常以分贝(符号是 dB)为单位来表示声音强度的等级,其中0 dB是人能听到的等级最低的声音. 一般地,如果强度为 的声音对应的等级为 dB,则有
(1)求等级为0 dB的声音的强度;(2)计算出90 dB的声音与60 dB的声音强度之比.
由例题可知,90 dB的声音强度是60 dB的声音强度的1000倍. 实际上,60 dB是一般说话的声音等级,而很嘈杂的马路的声音等级是90 dB. 为了保护听力,人所处的环境,声音一般不宜长时间超过90 dB.
实施模型,应用于实际.
知识层面:如何应用指数函数、对数函数和幂函数等具体函数的知识来解决实际生活中的相关问题.
思想方法:函数思想、方程思想、模型思想.
高中数学第四章 指数函数、对数函数与幂函数4.6 函数的应用(二)课堂教学ppt课件: 这是一份高中数学第四章 指数函数、对数函数与幂函数4.6 函数的应用(二)课堂教学ppt课件,共34页。PPT课件主要包含了即时巩固,数学建模,反思感悟,建立分段函数模型,图表型应用问题等内容,欢迎下载使用。
高中数学4.6 函数的应用(二)说课课件ppt: 这是一份高中数学4.6 函数的应用(二)说课课件ppt,共30页。PPT课件主要包含了学习目标,素养小结,备课素材等内容,欢迎下载使用。
高中数学人教B版 (2019)必修 第二册4.6 函数的应用(二)集体备课课件ppt: 这是一份高中数学人教B版 (2019)必修 第二册4.6 函数的应用(二)集体备课课件ppt,共60页。PPT课件主要包含了指数型函数模型,常见的函数模型,注意点,反思感悟,对数型函数模型,即声强级为60分贝,函数模型的选择问题,随堂演练,课时对点练,设至少需要过滤n次等内容,欢迎下载使用。













