2022-2023学年山东省德州市临邑县八年级（下）期末数学试卷（含解析）

这是一份2022-2023学年山东省德州市临邑县八年级（下）期末数学试卷（含解析），共27页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年山东省德州市临邑县八年级（下）期末数学试卷
一、选择题（本大题共12小题，共48.0分。在每小题列出的选项中，选出符合题目的一项）
1. 函数y=x x+4+1x−1的自变量x的取值范围是(    )
A. x≠−4且x≠1 B. x>−4且x≠1 C. x>−4 D. x≥−4且x≠1
2. 已知a，b，c是△ABC中∠A，∠B，∠C的对边，下列说法正确的有个．(    )
①若∠C=90°，则a2+b2=c2；
②若∠B=90°，则a2+c2=b2；
③若∠A=90°，则b2+c2=a2；
④总有a2+b2=c2．
A. 1 B. 2 C. 3 D. 4
3. 下列计算不正确的是(    )
A. 316= 34 B. 32+ 32=32
C. 3 2−2 2= 2 D. 2× 5= 10
4. 如图，在平面直角坐标系中，点A的坐标为(−2,3)，将点A绕原点O逆时针方向旋转90°得到点B，则点B的坐标为(    )
A. (−2,−3)
B. (−3,−2)
C. (2,3)
D. (3,2)
5. 下列命题为真命题的是(    )
A. 对角线互相垂直的平行四边形是正方形
B. 对角线相等的平行四边形为矩形
C. 一组对边平行另一组对边相等的四边形是平行四边形
D. 对角线互相垂直的四边形是菱形
6. 在同一平面直角坐标系中，一次函数y=ax+a2与y=a2x+a的图象可能是(    )
A. B. C. D.
7. 在2021年的体育学业水平测试中，6名学生的一项体育成绩统计如图所示，则这组数据的中位数、方差、众数分别是(    )
A. 18，1，18
B. 17.5，3，18
C. 18，3，18
D. 17.5，1，18
8. 如图，数轴上点A对应的数是0，点C对应的数是−4，BC⊥AC，垂足为C，且BC=1，以点A为圆心，AB长为半径画弧，交数轴于点D，则点D表示的数为(    )

A. − 17 B. 17 C. −4.2 D. −4.5
9. 对于一元二次方程ax2+bx+c=0(a≠0)，下列说法：
①若a+b+c=0，则b2−4ac≥0；
②若方程ax2+c=0有两个不相等的实根，则方程ax2+bx+c=0必有两个不相等的实根；
③若c是方程ax2+bx+c=0的一个很，则一定有ac+b+1=0成立；
④若x0是一元二次方程ax2+bx+c=0的根，则b2−4ac=(2ax0+b)2．
其中正确的(    )
A. ①②④ B. ①②③ C. ①③④ D. ②③④
10. 如图，在菱形ABCD中，AC=16，BD=12，E是CD边上一动点，过点E分别作EF⊥OC于点F，EF⊥OC于点G，连接FG，则FG的最小值为(    )
A. 4
B. 4.8
C. 5
D. 6
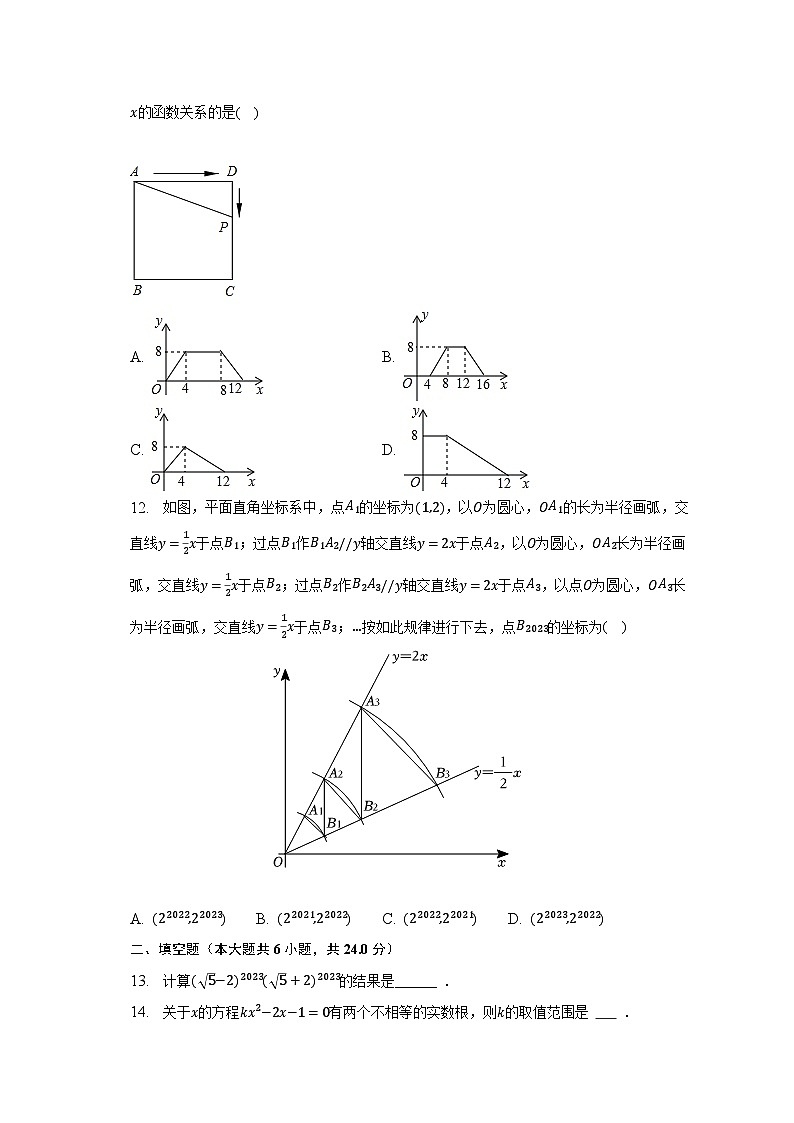
11. 如图，正方形ABCD的边长为4，P为正方形边上一动点，运动路线是A→D→C→B→A，设P点经过的路程为x，以点A、P、D为顶点的三角形的面积是y，则下列图象能大致反映y与x的函数关系的是(    )


A. B.
C. D.
12. 如图，平面直角坐标系中，点A1的坐标为(1,2)，以O为圆心，OA1的长为半径画弧，交直线y=12x于点B1；过点B1作B1A2//y轴交直线y=2x于点A2，以O为圆心，OA2长为半径画弧，交直线y=12x于点B2；过点B2作B2A3//y轴交直线y=2x于点A3，以点O为圆心，OA3长为半径画弧，交直线y=12x于点B3；…按如此规律进行下去，点B2023的坐标为(    )

A. (22022,22023) B. (22021,22022) C. (22022,22021) D. (22023,22022)
二、填空题（本大题共6小题，共24.0分）
13. 计算( 5−2)2023( 5+2)2023的结果是______ ．
14. 关于x的方程kx2−2x−1=0有两个不相等的实数根，则k的取值范围是        ．
15. 如图，把△ABC绕点C按顺时针方向旋转35°，得到△A′B′C，A′B′交AC于点D.若∠A′DC=90°，则∠A=          ．






16. 2023年，临邑县某单位为响应国家“厉行节约，反对浪费”的号召，减少了对办公经费的投入，在两个月内将开支从每月2500元降到1600元，若平均每月降低开支的百分率为x，则可根据题意列出方程为______ ．
17. 如图所示，直线y=23x+2分别与x轴、y轴交于点A、B，以线段AB为边，在第二象限内作等腰直角△ABC，∠BAC=90°，则过B、C两点直线的解析式为______ ．


18. 如图，正方形ABCD的对角线AC，BD交于点O，P为BD上的一点，连接CP，过点P作PF⊥CP交AD的延长线于点F，延长FP交AB于点E，则下列结论：(1)∠DPF=∠PCA；(2)BE=DF；(3)点P为EF的中点；(4)S△BPE=S△DCP；(5)若OP=2，则BE=2 2；其中正确的结论有______ 个.(填正确结论的个数)

三、解答题（本大题共7小题，共78.0分。解答应写出文字说明，证明过程或演算步骤）
19. (本小题10.0分)
(1)3 12−6 13+ 48；
(2)先化简，再求值：m−33m2−6m÷(m+2−5m−2)，其中m是方程x2+3x−4=0的根．
20. (本小题10.0分)
2023年2月6日土耳其发生7.8级地震，牵动世界各国人民的心！为进一步宣传防震减灾科普知识，增强学生应急避险和自救互救能力，某校组织全校学生进行“防震减灾知识测试”，现随机抽取部分学生的测试成绩x(单位：分)整理成A：60≤x0，b0，
∴方程ax2+bx+c=0必有两个不相等的实根，故②正确；
③∵c是方程ax2+bx+c=0的一个根，
则ac2+bc+c=0，
∴c(ac+b+1)=0，
若c=0，等式仍然成立，
但ac+b+1=0不一定成立，故③不正确；
④若x0是一元二次方程ax2+bx+c=0的根，
则由求根公式可得：x0=−b± b2−4ac2a，
∴2ax0+b=± b2−4ac，
∴b2−4ac=(2ax0+b)2，故④正确．
故正确的有①②④，
故选：A．
按照方程的解的含义、一元二次方程的实数根与判别式的关系、等式的性质、一元二次方程的求根公式等对各选项分别讨论，可得答案．
本题考查了一元二次方程根的判别式，灵活运用根的判别式式解题的关键．

10.【答案】B 
【解析】解：如图所示：连接OE，

在菱形ABCD中，AC=16，BD=12，
∴∠COD=90°,CD= OD2+OC2= 82+62=10，
∵EF⊥OC，EF⊥OC
∴四边形OGEF是矩形，
∴GF=OE，
∴FG的最小值，
即OE最小值，
∴当OE⊥AC时，OE最小，
∵12OC⋅OD=12CD⋅OE，
∴12×8×6=12×10⋅OE，
∴OE=4.8，
∴OE最小为4.8，
即FG的最小值为4.8，
故选：B．
如图所示：连接OE，在菱形ABCD中，AC=16，BD=12，得∠COD=90°，CD=10，由EF⊥OC，EF⊥OC，可得四边形OGEF是矩形，进而得出GF=OE，当OE⊥AC时，OE最小，即FG的最小值，即可得出．
本题主要考查了菱形的性质，矩形的判定与性质，垂线段最短，勾股定理，三角形的面积等知识，熟练掌握菱形的性质，证明四边形OGEF是矩形是解此题的关键．

11.【答案】B 
【解析】
【分析】
根据动点从点A出发，首先向点D运动，此时y=0，当点P在DC上运动时，y随着x的增大而增大，当点P在CB上运动时，y不变，当点P在BA上运动时，y随着x的增大而减小，据此作出选择即可．
本题考查了动点问题的函数图象，解决动点问题的函数图象问题关键是发现y随x的变化而变化的趋势．
【解答】
解：当点P由点A向点D运动，即0≤x≤4时，y的值为0；
当点P在DC上运动，即4−1且k≠0，
∴k的取值范围为k>−1且k≠0．
故答案为：k>−1且k≠0．
根据一元二次方程的定义和判别式，得出k≠0且Δ=(−2)2+4k>0，解出不等式，即可得到k的取值范围．
本题考查了一元二次方程根的判别式和一元二次方程的定义，解本题的关键在熟练掌握一元二次方程的根的判别式与根的个数的关系．一元二次方程的根的判别式与根的个数的关系：当Δ>0时，方程有两个不等的实数根；当Δ=0时，方程有两个相等的实数根；当Δ0的解集为x0，
∴w随着m的增大而增大，
当m=600时，w取得最大值，最大值为13000元，
1000−600=400(份)，
答：购进A菜品600份，B菜品400份，所获利润最大，最大利润为13000元． 
【解析】(1)设每份菜品A的利润为x元，每份菜品B的利润为y元，根据售出1份菜品A和2份菜品B可获利35元，售出2份菜品A和3份菜品B可获利60元，列二元一次方程组，求解即可；
(2)设购进A菜品m份，总利润为w元，根据菜品A的数量不高于菜品B数量的32，求出m的取值范围，再表示出w与m的函数关系式，根据一次函数的增减性即可确定最大利润时进货方案，进一步求出最大利润即可．
本题考查了一次函数的应用，二元一次方程组的应用，一元一次不等式的应用，理解题意是解题的关键．

25.【答案】(1)证明：∵四边形ABCD是正方形，
∴∠DAB=∠B=90°，DA=BA，
∵AF⊥DE，即∠AGD=90°，
∴∠GAE+∠GAD=90°=∠GAD+∠GDA，
∴∠ADE=∠BAF，
在△ABF与△DAE中，
∠BAF=∠ADEAB=DA∠B=∠DAE，
∴△ABF≌△DAE(ASA)；
(2)解：∵△ABF≌△DAE，
∴可设AE=BF=x，
∴BE=CF=4−x，
∴S△DEF=S正方形ABCD−S△ADE−S△EBF−S△DCF
=4×4−12×4x−12x(4−x)−12×4(4−x)
=16−2x−2x+12x2−8+2x
=12x2−2x+8，
∴12x2−2x+8=132，
解得x=3或x=1，
∴AE=3或AE=1，
∴AF= AD2+AE2=5或 17；
(3)解：如图所示，连接AM并延长交CD于点P，连接PF，

∵点M是DE的中点，
∴DM=ME，
∵在正方形ABCD中，AB//CD，
∴∠PDM=∠AEM，∠DPM=∠EAM，
∴△DPM≌△EAM(AAS)，
∴PM=AM，DP=AE=3或1，
当AE=3时，BF=DP=3，
∴CF=CP=1，
∴PF= PC2+CF2= 2，
∵N是AF的中点，
∴MN是△APF的中位线，
∴MN=12PF= 22；
当AE=1时，BF=DP=1，
∴CF=CP=3，
∴PF= PC2+CF2=3 2，
同理可得MN=12PF=3 22；
综上所述，MN的长度为 22或3 22． 
【解析】(1)先证得∠ADE=∠BAF，再利用ASA证明△DAE≌△ABF即可；
(2)根据全等三角形的性质可设AE=BF=x，则BE=CF=4−x，再由S△DEF=S正方形ABCD−S△ADE−S△EBF−S△DCF得到方程12x2−2x+8=132，解方程求出AE的值，再利用勾股定理求出AF的长即可；
(3)连接AM并延长交CD于点P，连接PF，可证明△DPM≌△EAM，得到PM=AM，再根据DP=AE=3或1，MN是△APF的中位线，求出PF的长即可．
本题考查正方形的性质、全等三角形的判定和性质以及勾股定理，三角形中位线定理，灵活运用所学知识是解题的关键．