2023年内蒙古省各市中考数学试题真题汇编——函数

这是一份2023年内蒙古省各市中考数学试题真题汇编——函数，共25页。试卷主要包含了乒乓球被誉为中国国球，定义等内容，欢迎下载使用。
函数（真题汇编）2023年内蒙古各市中考数学试题全解析版
一．选择题（共5小题）
1．（2023•内蒙古）在平面直角坐标系中，将正比例函数y＝﹣2x的图象向右平移3个单位长度得到一次函数y＝kx+b（k≠0）的图象，则该一次函数的解析式为（　　）
A．y＝﹣2x+3 B．y＝﹣2x+6 C．y＝﹣2x﹣3 D．y＝﹣2x﹣6
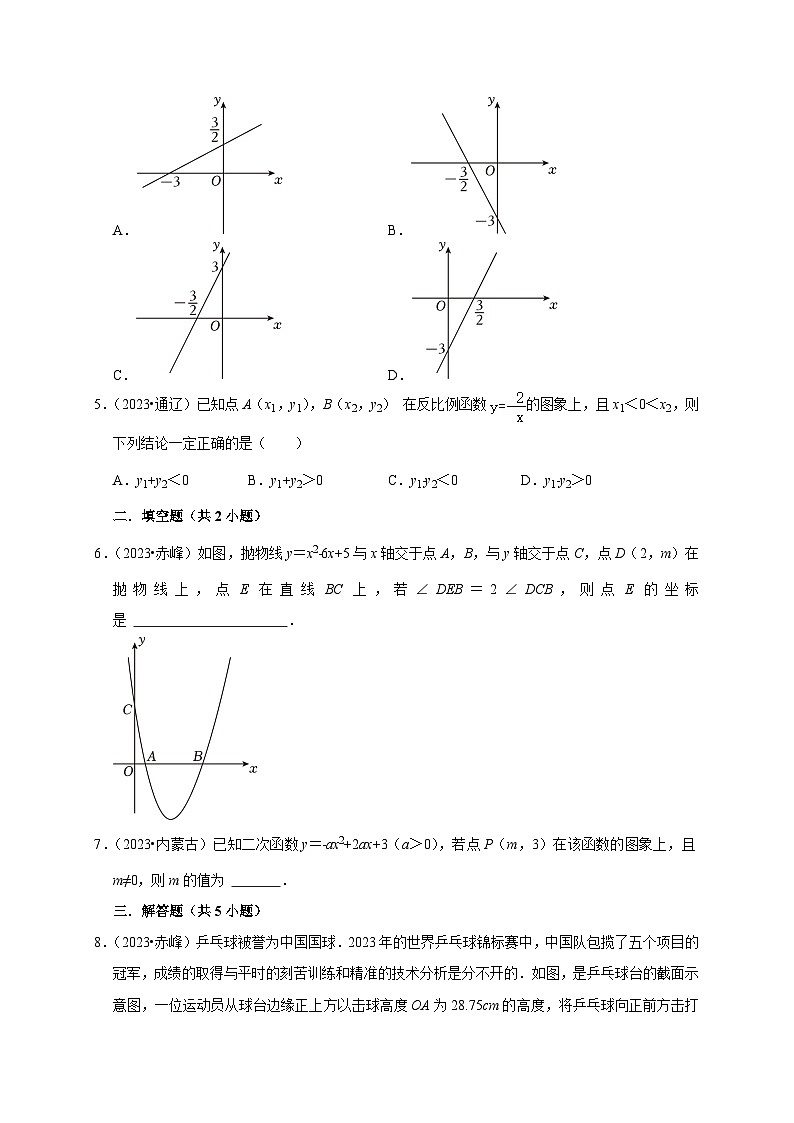
2．（2023•内蒙古）如图，在平面直角坐标系中，△OAB三个顶点的坐标分别为O（0，0），A（2，0），B（，1），△OA′B与△OAB关于直线OB对称，反比例函数y＝（k＞0，x＞0）的图象与A′B交于点C．若A′C＝BC，则k的值为（　　）

A．2 B． C． D．
3．（2023•通辽）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点（x1，0），（2，0），其中0＜x1＜1 下列四个结论：①abc＜0；②a+b+c＞0；③2b+3c＜0；④不等式ax2+bx+c＜﹣x+c的解集为0＜x＜2．其中正确结论的个数是（　　）

A．1 B．2 C．3 D．4
4．（2023•通辽）在平面直角坐标系中，一次函数y＝2x﹣3的图象是（　　）
A． B．
C． D．
5．（2023•通辽）已知点A（x1，y1），B（x2，y2） 在反比例函数的图象上，且x1＜0＜x2，则下列结论一定正确的是（　　）
A．y1+y2＜0 B．y1+y2＞0 C．y1﹣y2＜0 D．y1﹣y2＞0
二．填空题（共2小题）
6．（2023•赤峰）如图，抛物线y＝x2﹣6x+5与x轴交于点A，B，与y轴交于点C，点D（2，m）在抛物线上，点E在直线BC上，若∠DEB＝2∠DCB，则点E的坐标是 　 　．

7．（2023•内蒙古）已知二次函数y＝﹣ax2+2ax+3（a＞0），若点P（m，3）在该函数的图象上，且m≠0，则m的值为 　 　．
三．解答题（共5小题）
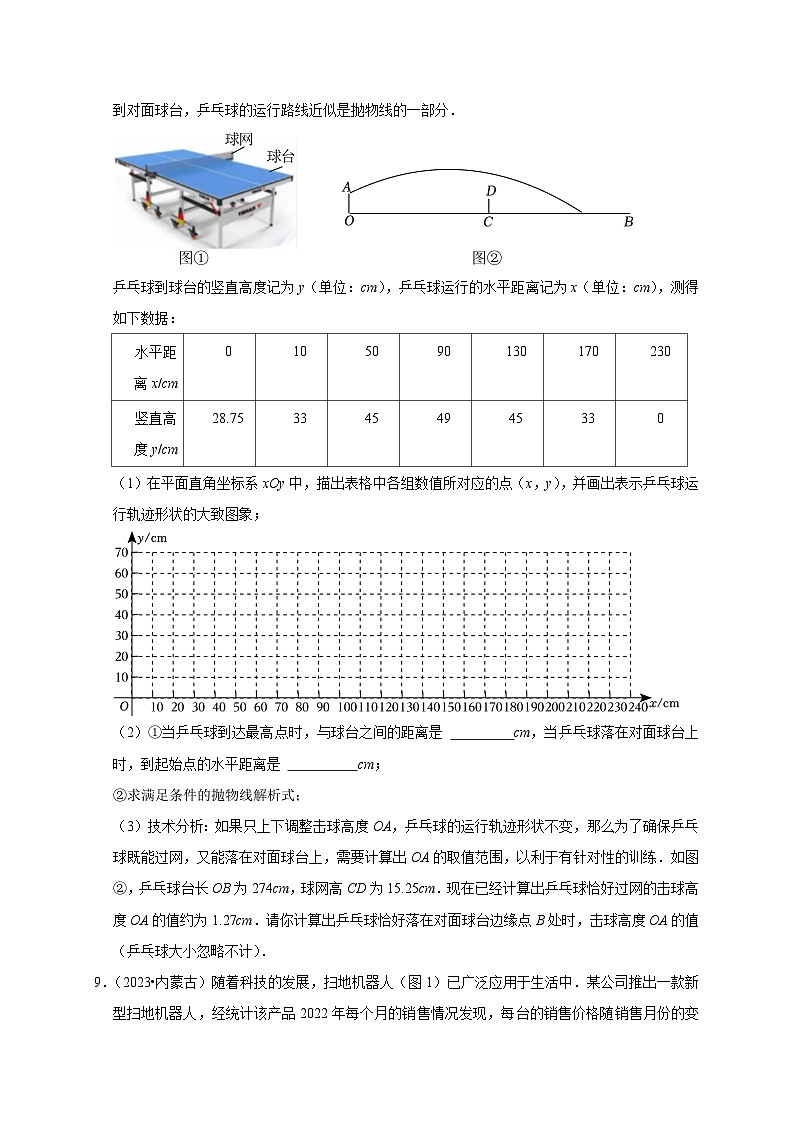
8．（2023•赤峰）乒乓球被誉为中国国球．2023年的世界乒乓球锦标赛中，中国队包揽了五个项目的冠军，成绩的取得与平时的刻苦训练和精准的技术分析是分不开的．如图，是乒乓球台的截面示意图，一位运动员从球台边缘正上方以击球高度OA为28.75cm的高度，将乒乓球向正前方击打到对面球台，乒乓球的运行路线近似是抛物线的一部分．

乒乓球到球台的竖直高度记为y（单位：cm），乒乓球运行的水平距离记为x（单位：cm），测得如下数据：
水平距离x/cm
0
10
50
90
130
170
230
竖直高度y/cm
28.75
33
45
49
45
33
0
（1）在平面直角坐标系xOy中，描出表格中各组数值所对应的点（x，y），并画出表示乒乓球运行轨迹形状的大致图象；

（2）①当乒乓球到达最高点时，与球台之间的距离是 　 　cm，当乒乓球落在对面球台上时，到起始点的水平距离是 　 　cm；
②求满足条件的抛物线解析式；
（3）技术分析：如果只上下调整击球高度OA，乒乓球的运行轨迹形状不变，那么为了确保乒乓球既能过网，又能落在对面球台上，需要计算出OA的取值范围，以利于有针对性的训练．如图②，乒乓球台长OB为274cm，球网高CD为15.25cm．现在已经计算出乒乓球恰好过网的击球高度OA的值约为1.27cm．请你计算出乒乓球恰好落在对面球台边缘点B处时，击球高度OA的值（乒乓球大小忽略不计）．
9．（2023•内蒙古）随着科技的发展，扫地机器人（图1）已广泛应用于生活中．某公司推出一款新型扫地机器人，经统计该产品2022年每个月的销售情况发现，每台的销售价格随销售月份的变化而变化．设该产品2022年第x（x为整数）个月每台的销售价格为y（单位：元），y与x的函数关系如图2所示（图中ABC为一折线）．

（1）当1≤x≤10时，求每台的销售价格y与x之间的函数关系式；
（2）设该产品2022年第x个月的销售数量为m（单位：万台），m与x的关系可以用m＝x+1来描述、求哪个月的销售收入最多，最多为多少万元？（销售收入＝每台的销售价格×销售数量）
10．（2023•赤峰）定义：在平面直角坐标系xOy中，当点N在图形M的内部，或在图形M上，且点N的横坐标和纵坐标相等时，则称点N为图形M的“梦之点”．
（1）如图①，矩形ABCD的顶点坐标分别是A（﹣1，2），B（﹣1，﹣1），C（3，﹣1），D（3，2），在点M1（1，1），M2（2，2），M3（3，3）中，是矩形ABCD“梦之点“的是 　 　；
（2）点G（2，2）是反比例函数y1＝图象上的一个“梦之点”，则该函数图象上的另一个“梦之点”H的坐标是 　 　，直线GH的解析式是y2＝　 　，y1＞y2时，x的取值范围是 　 　；
（3）如图②，已知点A，B是抛物线y＝﹣x2+x+上的“梦之点”，点C是抛物线的顶点．连接AC，AB，BC，判断△ABC的形状，并说明理由．

11．（2023•通辽）在平面直角坐标系中，已知抛物线 与x轴交于点A（1，0）和点B，与y轴交于点C（0，﹣4）．

（1）求这条抛物线的函数解析式；
（2）P是抛物线上一动点（不与点A，B，C重合），作PD⊥x轴，垂足为D，连接PC．
①如图，若点P在第三象限，且tan∠CPD＝2，求点P的坐标；
②直线PD交直线BC于点E，当点E关于直线PC的对称点E′落在y轴上时，请直接写出四边形PECE'的周长．
12．（2023•内蒙古）如图，在平面直角坐标系中，抛物线y＝﹣x2+3x+1交y轴于点A，直线y＝﹣x+2交抛物线于B，C两点（点B在点C的左侧），交y轴于点D，交x轴于点E．
（1）求点D，E，C的坐标；
（2）F是线段OE上一点（OF＜EF），连接AF，DF，CF，且AF2+EF2＝21．
①求证：△DFC是直角三角形；
②∠DFC的平分线FK交线段DC于点K，P是直线BC上方抛物线上一动点，当3tan∠PFK＝1时，求点P的坐标．


函数（真题汇编）2023年内蒙古各市中考数学试题全解析版
参考答案与试题解析
一．选择题（共5小题）
1．（2023•内蒙古）在平面直角坐标系中，将正比例函数y＝﹣2x的图象向右平移3个单位长度得到一次函数y＝kx+b（k≠0）的图象，则该一次函数的解析式为（　　）
A．y＝﹣2x+3 B．y＝﹣2x+6 C．y＝﹣2x﹣3 D．y＝﹣2x﹣6
【答案】B
【解答】解：正比例函数y＝﹣2x的图象向右平移3个单位长度得到一次函数的解析式为y＝﹣2（x﹣3）＝﹣2x+6．
故选：B．
2．（2023•内蒙古）如图，在平面直角坐标系中，△OAB三个顶点的坐标分别为O（0，0），A（2，0），B（，1），△OA′B与△OAB关于直线OB对称，反比例函数y＝（k＞0，x＞0）的图象与A′B交于点C．若A′C＝BC，则k的值为（　　）

A．2 B． C． D．
【答案】A
【解答】解：如图，过点B作BD⊥x轴于点D，
∵O（0，0），A（2，0），B（，1），
∴BD＝1，OD＝，
∴AD＝OD＝，tan∠BOA＝＝，
∴OB＝AB＝＝2，∠BOA＝∠BAO＝30°，
∴∠OBD＝∠ABD＝60°，∠OBA＝120°，
∵△AOB与△A′OB关于直线OB对称，
∴∠OBA′＝120°，
∴∠OBA′+∠OBD＝180°，
∴点A′、B、D共线，
∴A′B＝AB＝2，
∵A′C＝BC，
∴BC＝1，CD＝2，
∴点C（，2），
∵点C（，2）在反比例函数y＝的图象上，
∴k＝×2＝2，
故选：A．

3．（2023•通辽）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点（x1，0），（2，0），其中0＜x1＜1 下列四个结论：①abc＜0；②a+b+c＞0；③2b+3c＜0；④不等式ax2+bx+c＜﹣x+c的解集为0＜x＜2．其中正确结论的个数是（　　）

A．1 B．2 C．3 D．4
【答案】C
【解答】解：∵抛物线开口向上，对称轴在y轴右边，与y轴交于正半轴，
∴a＞0，b＜0，c＞0，
∴abc＜0，
∴①正确．
∵当x＝1时，y＜0，
∴a+b+c＜0，
∴②错误．
∵抛物线过点（2，0），
∴4a+2b+c＝0，
∴b＝﹣2a﹣，a＝﹣，
∵a+b+c＜0，
∴a﹣2a﹣+c＜0，
∴2a﹣c＞0，
∴﹣b﹣c﹣c＞0，
∴﹣2b﹣3c＞0，
∴2b+3c＜0，
∴③正确．
如图：

设y1＝ax2+bx+c，y2＝﹣x+c，
由图值，y1＜y2时，0＜x＜2，
故④正确．
故选：C．
4．（2023•通辽）在平面直角坐标系中，一次函数y＝2x﹣3的图象是（　　）
A． B．
C． D．
【答案】D
【解答】解：∵一次函数y＝2x﹣3中的k＝2＞0，b＝﹣3＜0，
∴一次函数y＝2x﹣3的图象经过第一、三、四象限．
故选：D．
5．（2023•通辽）已知点A（x1，y1），B（x2，y2） 在反比例函数的图象上，且x1＜0＜x2，则下列结论一定正确的是（　　）
A．y1+y2＜0 B．y1+y2＞0 C．y1﹣y2＜0 D．y1﹣y2＞0
【答案】D
【解答】解：∵反比例函数的图象在二、四象限，而x1＜0＜x2，
∴点A（x1，y1）在第二象限反比例函数的图象上，B（x2，y2） 在第四象限反比例函数的图象上，
∴y1＞0＞y2，
∴y1﹣y2＞0，
故选：D．
二．填空题（共2小题）
6．（2023•赤峰）如图，抛物线y＝x2﹣6x+5与x轴交于点A，B，与y轴交于点C，点D（2，m）在抛物线上，点E在直线BC上，若∠DEB＝2∠DCB，则点E的坐标是 　 和 　．

【答案】 和 ．
【解答】解：根据D点坐标，有m＝22﹣6×2+5＝﹣3，所，以D点坐标（2，﹣3），

设BC所在直线解析式为 y＝kx+b，其过点C（0，5）、B（5，0），
，
解得，
BC所在直线的解析式为：y＝﹣x+5，
当E点在线段BC上时，设E（a，﹣a+5），∠DEB＝∠DCE+∠CDE，而∠DEB＝2∠DCB，
∴∠DCE＝∠CDE，
∴CE＝DE，
因为E（a，﹣a+5），C（0，5），D（2，﹣3），
有，
解得：，，所以E点的坐标为：，
当E在CB的延长线上时，
在△BDC中，BD2＝（5﹣2）2+32＝18，
BC2＝52+52＝50，DC2＝（5+3）2+22＝68，
BD2+BC2＝DC2，
∴BD⊥BC 如图延长EB至 E'，取 BE'＝BE，

则有△DEE'为等腰三角形，DE＝DE'，
∴∠DEE′＝∠DE′E，
又∵∠DEB＝2∠DCB，
∴∠DE′E＝2∠DCB，
则E′为符合题意的点，
∵OC＝OB＝5∠OBC＝45°，
E′的横坐标：，纵坐标为 ；
综上E点的坐标为： 和 ．
7．（2023•内蒙古）已知二次函数y＝﹣ax2+2ax+3（a＞0），若点P（m，3）在该函数的图象上，且m≠0，则m的值为 　2　．
【答案】2．
【解答】解：∵点P（m，3）在二次函数y＝﹣ax2+2ax+3（a＞0）的图象上，
∴3＝﹣am2+2am+3，
∴﹣am（m﹣2）＝0，
解得m＝2或m＝0（舍去），
故答案为：2．
三．解答题（共5小题）
8．（2023•赤峰）乒乓球被誉为中国国球．2023年的世界乒乓球锦标赛中，中国队包揽了五个项目的冠军，成绩的取得与平时的刻苦训练和精准的技术分析是分不开的．如图，是乒乓球台的截面示意图，一位运动员从球台边缘正上方以击球高度OA为28.75cm的高度，将乒乓球向正前方击打到对面球台，乒乓球的运行路线近似是抛物线的一部分．

乒乓球到球台的竖直高度记为y（单位：cm），乒乓球运行的水平距离记为x（单位：cm），测得如下数据：
水平距离x/cm
0
10
50
90
130
170
230
竖直高度y/cm
28.75
33
45
49
45
33
0
（1）在平面直角坐标系xOy中，描出表格中各组数值所对应的点（x，y），并画出表示乒乓球运行轨迹形状的大致图象；

（2）①当乒乓球到达最高点时，与球台之间的距离是 　49　cm，当乒乓球落在对面球台上时，到起始点的水平距离是 　230　cm；
②求满足条件的抛物线解析式；
（3）技术分析：如果只上下调整击球高度OA，乒乓球的运行轨迹形状不变，那么为了确保乒乓球既能过网，又能落在对面球台上，需要计算出OA的取值范围，以利于有针对性的训练．如图②，乒乓球台长OB为274cm，球网高CD为15.25cm．现在已经计算出乒乓球恰好过网的击球高度OA的值约为1.27cm．请你计算出乒乓球恰好落在对面球台边缘点B处时，击球高度OA的值（乒乓球大小忽略不计）．
【答案】（1）画函数图象见解答过程；
（2）①49；230；②y＝﹣0.0025（x﹣90）2+49；
（3）乒乓球恰好落在对面球台边缘点B处时，击球高度OA的值为64.39cm．
【解答】解：（1）描出各点，画出图象如下：

（2）①观察表格数据，可知当x＝50和x＝130 时，函数值相等，
∴对称轴为直线x＝＝90，顶点坐标为（90，49），
∵抛物线开口向下，
∴最高点时，乒乓球与球台之间的距离是49cm，
当y＝0时，x＝230，
∴乒乓球落在对面球台上时，到起始点的水平距离是230cm；
故答案为：49；230；
②设抛物线解析式为y＝a（x﹣90）2+49，
将（230，0）代入得，0＝a（230﹣90）2+49，
解得：a＝﹣0.0025，
∴抛物线解析式为y＝﹣0.0025（x﹣90）2+49；
（3）当OA＝28.75 时，抛物线的解析式为 y＝﹣0.0025（x﹣90）2+49，
设乒乓球恰好落在对面球台边缘点B处时，击球高度OA的值为h，则平移距离为（h﹣28.75）cm，
∴平移后的抛物线的解析式为 y＝﹣0.0025（x﹣90）2+49+h﹣28.75，
当x＝274 时，y＝0，
∴﹣0.0025（274﹣90）2+49+h﹣28.75＝0，
解得：h＝64.39；
答：乒乓球恰好落在对面球台边缘点B处时，击球高度OA的值为64.39cm．
9．（2023•内蒙古）随着科技的发展，扫地机器人（图1）已广泛应用于生活中．某公司推出一款新型扫地机器人，经统计该产品2022年每个月的销售情况发现，每台的销售价格随销售月份的变化而变化．设该产品2022年第x（x为整数）个月每台的销售价格为y（单位：元），y与x的函数关系如图2所示（图中ABC为一折线）．

（1）当1≤x≤10时，求每台的销售价格y与x之间的函数关系式；
（2）设该产品2022年第x个月的销售数量为m（单位：万台），m与x的关系可以用m＝x+1来描述、求哪个月的销售收入最多，最多为多少万元？（销售收入＝每台的销售价格×销售数量）
【答案】（1）当1≤x≤10时，每台的销售价格y与x之间的函数关系式为y＝﹣150x+3000；
（2）第5个月的销售收入最多，最多为3375万元．
【解答】解：（1）当1≤x≤10时，设每台的销售价格y与x之间的函数关系式为y＝kx+b（k≠0），
∵图象过A（1，2850），B（10，1500）两点，
∴，
解得，
∴当1≤x≤10时，每台的销售价格y与x之间的函数关系式为y＝﹣150x+3000；
（2）设销售收入为w万元，
①当1≤x≤10时，w＝（﹣150x+3000）（x+1）＝﹣15（x﹣5）2+3375，
∵﹣15＜0，
∴当x＝5时，w最大＝3375 （万元）；
②当10＜x≤12时，w＝1500（x+1）＝150x+1500，
∴w随x的增大而增大，
∴当x＝12时，w最大＝150×12+1500＝3300 （万元）；
∵3375＞3300，
∴第5个月的销售收入最多，最多为3375万元．
10．（2023•赤峰）定义：在平面直角坐标系xOy中，当点N在图形M的内部，或在图形M上，且点N的横坐标和纵坐标相等时，则称点N为图形M的“梦之点”．
（1）如图①，矩形ABCD的顶点坐标分别是A（﹣1，2），B（﹣1，﹣1），C（3，﹣1），D（3，2），在点M1（1，1），M2（2，2），M3（3，3）中，是矩形ABCD“梦之点“的是 　M1，M2　；
（2）点G（2，2）是反比例函数y1＝图象上的一个“梦之点”，则该函数图象上的另一个“梦之点”H的坐标是 　H（﹣2，﹣2）　，直线GH的解析式是y2＝　x　，y1＞y2时，x的取值范围是 　x＜﹣2或0＜x＜2　；
（3）如图②，已知点A，B是抛物线y＝﹣x2+x+上的“梦之点”，点C是抛物线的顶点．连接AC，AB，BC，判断△ABC的形状，并说明理由．

【答案】（1）M1，M2；
（2）H（﹣2，﹣2），x，x＜﹣2或0＜x＜2；
（3）△ABC是直角三角形，理由见解析．
【解答】解：（1）∵矩形ABCD的顶点坐标分别是A（﹣1，2），B（﹣1，﹣1），C（3，﹣1），D（3，2），
∴矩形ABCD的“梦之点”（x，y）满足﹣1≤x≤3，﹣1≤y≤2，
∴点M1（1，1），M2（2，2）是矩形ABCD的“梦之点”，点M3（3，3）不是矩形ABCD的“梦之点”，
故答案为：M1，M2；
（2）∵点G（2，2）是反比例函数y1＝图象上的一个“梦之点”，
∴把G（2，2）代入y1＝得k＝4，
∴y1＝，
∵“梦之点”的横坐标和纵坐标相等，
∴“梦之点”都在y＝x的图象上，联立，
解得或，
∴H（﹣2，﹣2），
∴直线GH的解析式为y2＝x，
∴y1＞y2时，x的取值范围是x＜﹣2或0＜x＜2，
故答案为：H（﹣2，﹣2），x，x＜﹣2或0＜x＜2；
（3）△ABC是直角三角形，
理由：∵点A，B是抛物线y＝﹣上的“梦之点”，
∴，
解得或，
∴A（3，3），B（﹣3，﹣3），
∵y＝﹣＝﹣（x﹣1）2+5，
∴顶点C（1，5），
∴AC2＝（3﹣1）2+（3﹣5）2＝8，AB2＝（﹣3﹣3）2+（﹣3﹣3）2＝72，BC2＝（﹣3﹣1）2+（﹣3﹣5）2＝80，
∴BC2＝AC2+AB2，
∴△ABC是直角三角形．
11．（2023•通辽）在平面直角坐标系中，已知抛物线 与x轴交于点A（1，0）和点B，与y轴交于点C（0，﹣4）．

（1）求这条抛物线的函数解析式；
（2）P是抛物线上一动点（不与点A，B，C重合），作PD⊥x轴，垂足为D，连接PC．
①如图，若点P在第三象限，且tan∠CPD＝2，求点P的坐标；
②直线PD交直线BC于点E，当点E关于直线PC的对称点E′落在y轴上时，请直接写出四边形PECE'的周长．
【答案】（1）．
（2）①P（﹣．
②或．
【解答】解：（1）∵抛物线 与x轴交于点A（1，0）和点B，与y轴交于点C（0，﹣4），
∴，
解得，
∴抛物线的解析式为．
答：抛物线的解析式为．
（2）①设P（x，），如图，过点C作CE⊥PD于E，

∴∠PEC＝∠CED＝90°，
∵C（0，﹣4），
∴OC＝4，
∵PD⊥x轴，
∴∠PDO＝90°，
∵∠DOC＝90°，
∴四边形DOCE是矩形，
∴DE＝OC＝4，OD＝CE＝﹣x，
∴＝，
∵，
∴，
∴（舍去），
∴＝，
∴P（﹣．
②设P（m，），
对于，当y＝0时，，
解得x1＝1，x2＝﹣3，
∴B（﹣3，0），
∵OC＝4，
∴，
当点P在第三象限时，如图，过点E作EF⊥y轴于F，

则四边形DEFO是矩形，
∴EF＝OD＝﹣m，
∵点E与点E′关于PC对称，
∴∠ECP＝∠E′CP，CE＝CE′，
∵PE∥y轴，
∴∠EPC＝∠PCE′，
∴PE＝CE，
∴PE＝CE′，
∴四边形PECE′是菱形，
∵EF∥OA，
∴△CEF∽△CBO，
∴，
∴，
∴，
设直线BC的解析式为y＝kx+b，
∴，
解得，
∴直线BC的解析式为y＝﹣x﹣4，
∴，
∴＝，
∵，PE＝CE，
∴，
解得（舍去），
∴，
∴四边形PECE′的周长C＝4CE＝4×＝，
当点P在第二象限时，如图，

同理可得，
解得（舍去），
∴，
∴四边形PECE′的周长C＝4CE＝4×＝，
综上，四边形PECE′的周长为或．
12．（2023•内蒙古）如图，在平面直角坐标系中，抛物线y＝﹣x2+3x+1交y轴于点A，直线y＝﹣x+2交抛物线于B，C两点（点B在点C的左侧），交y轴于点D，交x轴于点E．
（1）求点D，E，C的坐标；
（2）F是线段OE上一点（OF＜EF），连接AF，DF，CF，且AF2+EF2＝21．
①求证：△DFC是直角三角形；
②∠DFC的平分线FK交线段DC于点K，P是直线BC上方抛物线上一动点，当3tan∠PFK＝1时，求点P的坐标．

【答案】（1）C（3，1），D（0，2），E（6，0）．
（2）①证明见解答；
②点P的坐标为（1，3）或（）．
【解答】（1）解：∵直线y＝﹣x+2交y轴于点D，交x轴于点E，
当x＝0时，y＝2，
∴D（0，2），
当y＝0时，x＝6，
∴E（6，0），
∵直线y＝﹣x+2交抛物线于B，C两点（点B在点C的左侧），
∴﹣x2+3x+1＝﹣x+2，
∴3x2﹣10x+3＝0，
解得，
∵点B在点C的左侧，
∴点C的横坐标为3，当x＝3时，y＝1，
∴C（3，1），
答：C（3，1），D（0，2），E（6，0）．
（2）如图，

①证明：∵抛物线y＝﹣x2+3x+1交y轴于点A，
当x＝0时，y＝1，
∴A（0，1），
∴OA＝1，
在Rt△AOF中，∠AOF＝90°，
∴AF2＝OA2+OF2，
设F（m，0），
∴OF＝m，
∴AF2＝1+m2，
∵E（6，0），
∴OE＝6，
∴EF＝OE﹣OF＝6﹣m，
∵AF2+EF2＝21，
∴1+m2+（6﹣m）2＝21，
∴m1＝2，m2＝4，
∵OF＜EF，
∴m＝2，
∴OF＝2，
∴F（2，0），
∵D（0，2），
∴OD＝2，
∴OD＝OF，
∴△DOF是等腰直角三角形，
∴∠OFD＝45°，
过点C作CG⊥x轴于G，
∵C（3，1），
∴CG＝1，OG＝3，
∵GF＝OG﹣OF＝1，
∴CG＝GF，
∴△CGF是等腰直角三角形，
∴∠GFC＝45°，
∴∠DFC＝90°，
∴△DFC是直角三角形．
②解：∵FK平分∠DFC，∠DFC＝90°，
∴∠DEK＝∠CFK＝45°，
∴∠OFK＝∠OFD+∠DFK＝90°，
∴FK∥y轴，
∵3tan∠PFK＝1，
∴，
设点P的坐标为（t，﹣t2+3t+1），根据题意得．
（i）当点P在直线KF的左侧抛物线上时，．
过点P1作P1H⊥x轴于H，
∴P1H∥KF，
∴∠HP1F＝∠P1FK，
∴，
∵HF＝OF﹣OH，
∴HF＝2﹣t，
在Rt△P1HF中，∵，
∴P1H＝3HF，
∵，
∴﹣t2+3t+1＝3（2﹣t），
∴t2﹣6t+5＝0，
∴t1＝1，t2＝5（舍去），
当t＝1时，﹣t2+3t+1＝3，
∴P1（1，3）．
（ii）当点P在直线KF的右侧抛物线上时，，
过点P2作P2M⊥x轴于M，
∴P2M∥KF，
∴∠MP2F＝∠P2FK，
∴，
∴P2M＝3MF，
∵，
∴﹣t2+3t+1＝3（t﹣2），
∴（舍去），
当t＝时，，
∴．
∴点P的坐标为（1，3）或（）．