2024年新高考数学第一轮复习课件：第43讲　抛物线

这是一份2024年新高考数学第一轮复习课件：第43讲　抛物线，共35页。PPT课件主要包含了激活思维，x2＝3y，基础回归，几个常用结论，研题型·融会贯通，举题说法，随堂内化等内容，欢迎下载使用。
1. (人A 选必一P132例1改)抛物线y2＝4x的焦点坐标是(　 　)A. (0,2) B. (0,1)C. (2,0) D. (1,0)
【解析】 由题意知，抛物线的准线方程为y＝－1，所以由抛物线的定义知，点A到抛物线焦点的距离为5.
3. (人A 选必一P135例4改)已知直线l过抛物线x2＝2py(p>0)的焦点，且与抛物线交于A，B两点，若线段AB的长是6，AB的中点到x轴的距离是1，则此抛物线的方程是(　 　)A. x2＝12y B. x2＝8y C. x2＝6y D. x2＝4y
【解析】 设A(x1，y1)，B(x2，y2)，则|AB|＝y1＋y2＋p＝2＋p＝6，所以p＝4，即抛物线的方程为x2＝8y.
4. (人A 选必一P135例4改)已知抛物线x2＝ay与直线y＝2x－2交于M，N两点，若MN中点的横坐标为3，则此抛物线的方程为______________.
5. (人A 选必一P134例3改)已知抛物线y2＝2px(p>0)上一点M(3，t)与焦点F的距离|MF|＝p，则点M到坐标原点O的距离为________.
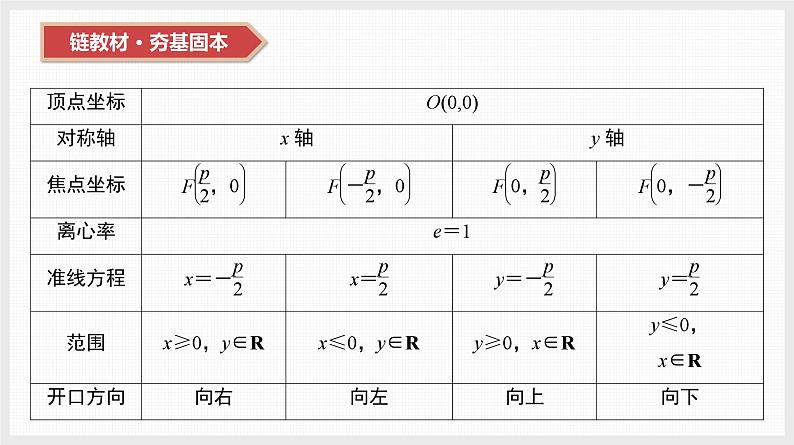
1. 抛物线的概念平面内与一个定点F和一条定直线l(l不经过点F)的距离________的点的轨迹叫做抛物线，点F叫做抛物线的________，直线l叫做抛物线的________.2. 抛物线的标准方程与几何性质
A. 点M到焦点的距离为3B. 直线MF与x轴垂直C. 直线MF与C交于点N，以弦MN为直径的圆与C的准线相切D. 过点M与C相切的直线方程为x－2y＋1＝0
由焦点F(1,0)知直线MF不与x轴垂直，故B错误；
(2) (2022·菏泽一模)(多选)设抛物线C：y2＝8x的焦点为F，准线为l，点M为C上一动点，E(3,1)为定点，则下列结论正确的是(　 　)A. 准线l的方程是y＝－2B. 以线段MF为直径的圆与y轴相切C. |ME|＋|MF|的最小值为5D. |ME|－|MF|的最大值为2
【解析】 对于A，由抛物线C：y2＝8x，可得焦点F的坐标为(2,0)，准线方程为x＝－2，故A错误；
对于C，如图(1)，过点M作准线的垂线，垂足为N，由抛物线的定义得|MF|＝|MN|，所以|ME|＋|MF|＝|ME|＋|MN|，由图可得，当E，M，N三点共线时，|ME|＋|MN|取得最小值，即为|EN′|＝3＋2＝5，所以|ME|＋|MF|的最小值为5，故C正确；图(1)
利用抛物线的定义可以解决距离的最值问题，该类问题一般情况下都与抛物线的定义有关，实现由点到点的距离与点到直线的距离的转化．(1) 将抛物线上的点到准线的距离转化为该点到焦点的距离，构造出“两点之间线段最短”，使问题得以解决．(2) 将抛物线上的点到焦点的距离转化为该点到准线的距离，利用“与直线上所有点的连线中垂线段最短”原理解决．
A. 30° B. 45° C. 60° D. 90°
又由抛物线的定义知|AB|＝|AF|，故∠BFA＝45°，则∠BAF＝90°.
(2) 已知抛物线C：x2＝2y上有两动点P，Q，且|PQ|＝5，则线段PQ的中点到x轴距离的最小值是______.
A. 0 B. 1 C. 2 D. 3
综上，只有乙是“直线AB经过焦点F”的充要条件．
焦点弦的相关结论，详见“基础回归”第3点．
【解答】 由题意，点P到点F的距离等于点P到直线x＝－1的距离，所以点P的轨迹是以F(1,0)为焦点，直线x＝－1为准线的抛物线，p＝2，故曲线E的方程是y2＝4x.
例3　设点F(1,0)，动圆经过点F且和直线x＝－1相切，记动圆的圆心P的轨迹为曲线E.(1) 求曲线E的方程；
(2) 过点F的直线交曲线E于A，B两点，另一条与直线AB平行的直线交x轴于点M，交y轴于点N，若△NAB是以点N为直角顶点的等腰直角三角形，求点M的横坐标．
由题意△NAB是以点N为直角顶点的等腰直角三角形，故NC⊥AB，过C与AB垂直的直线，其方程为y＝－m(x－2m2－1)＋2m，令x＝0，得y＝2m3＋3m，故点N的坐标为(0,2m3＋3m)．
利用抛物线的定义求其方程以及直线和抛物线相交时和三角形有关的点的坐标问题时，解答的思路一般是设直线方程，与抛物线方程联立，利用根与系数的关系表示出相关等量关系，再化简整理，关键就是运算量较大且比较繁杂，要十分细 心．
1. 若抛物线x2＝my上一点(t,2)到其焦点的距离等于4，则m等于(　 　)A. 8 B. 4
点击对应数字即可跳转到对应题目
A. 1 B. 2 C. 3 D. 4
3. (2022·深圳二模)过抛物线y2＝2px(p>0)的焦点F作直线l，交抛物线于A，B两点，若|FA|＝3|FB|，则直线l的倾斜角等于(　 　)A. 30°或150° B. 45°或135°C. 60°或120° D. 与p值有关
因为|FA|＝3|FB|，所以|AM|＝2|BF|，|AB|＝4|BF|，所以∠ABM＝30°，即直线l的倾斜角等于∠AFx＝60°.同理可得直线l的倾斜角为120°时，也满足题意．
4. (2022·湛江二模)拋物线C：y2＝2px(p>0)的焦点为F，点P(2，m)为C上一点，若|PF|＝3，则m＝__________.