





2024年新高考数学第一轮复习课件:第46讲 第1课时 变量的相关关系及线性回归模型
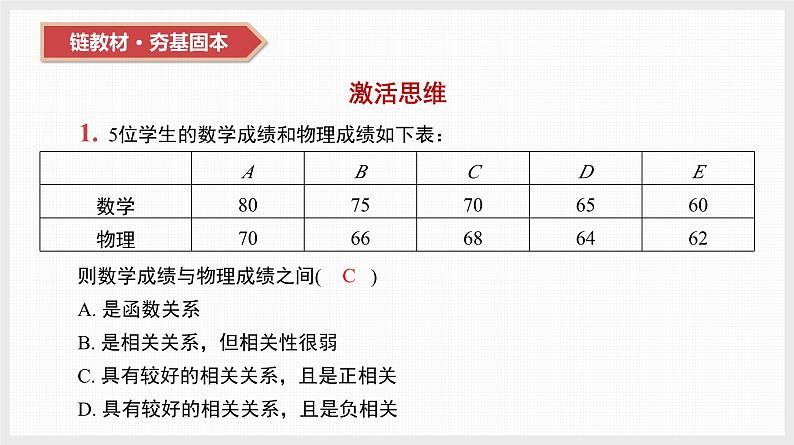
展开1. 5位学生的数学成绩和物理成绩如下表:则数学成绩与物理成绩之间( )A. 是函数关系B. 是相关关系,但相关性很弱C. 具有较好的相关关系,且是正相关D. 具有较好的相关关系,且是负相关
2. 已知变量x,y之间具有线性相关关系,其散点图如图所示,则其经验回归方程可能为( )
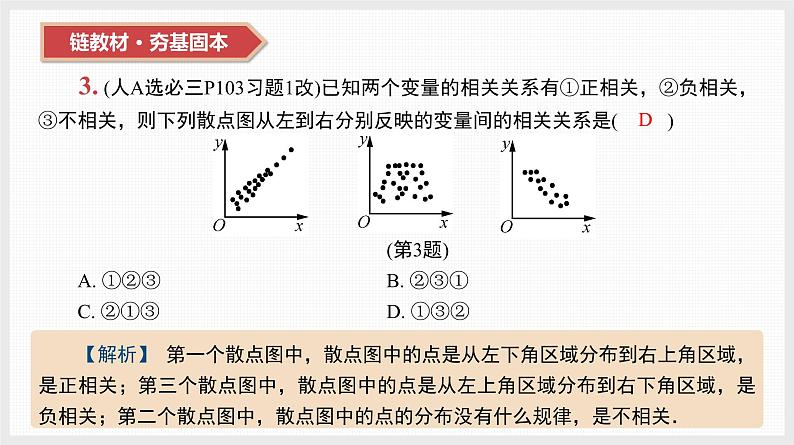
3. (人A选必三P103习题1改)已知两个变量的相关关系有①正相关,②负相关,③不相关,则下列散点图从左到右分别反映的变量间的相关关系是( ) (第3题)A. ①②③ B. ②③①C. ②①③ D. ①③②
【解析】 第一个散点图中,散点图中的点是从左下角区域分布到右上角区域,是正相关;第三个散点图中,散点图中的点是从左上角区域分布到右下角区域,是负相关;第二个散点图中,散点图中的点的分布没有什么规律,是不相关.
4. 下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x(单位:t)与相应的生产能耗y(单位:t)的几组对应数据:
1. 变量的相关关系(1) 相关关系两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.(2) 相关关系的分类:正相关和负相关.(3) 线性相关一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在__________附近,我们就称这两个变量线性相关.一般地,如果两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关.
2. 样本相关系数(1) 相关系数r的计算变量x和变量y的样本相关系数r的计算公式如下:
(2) 相关系数r的性质①当__________时,称成对样本数据______相关;当________0时,称成对样本数据______相关;当r=0时,称成对样本数据间没有线性相关关系.②样本相关系数r的取值范围为________________.当|r|越接近1时,成对样本数据的线性相关程度越______;当|r|越接近0时,成对样本数据的线性相关程度越______.
3. 一元线性回归模型
第1课时 变量的相关关系及线性回归模型
例1 (2022·重庆诊断)某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
根据表中数据,下列说法正确的是( )A. 利润率与人均销售额成正相关关系B. 利润率与人均销售额成负相关关系C. 利润率与人均销售额成正比例函数关系D. 利润率与人均销售额成反比例函数关系
【解析】 由统计表可得利润率与人均销售额不是正比例关系,也不是反比例关系,排除C和D;其属于正相关关系,A正确,B错误.
判定两个变量相关性的方法(1) 画散点图:点的分布从左下角到右上角,两个变量正相关;点的分布从左上角到右下角,两个变量负相关.(2) 相关系数:当r>0时,正相关;当r<0时,负相关;|r|越接近于1,相关性越强.
在一次对人体脂肪含量和年龄的关系的研究中,研究人员获得了一组样本数据,并制成如图所示的人体脂肪含量与年龄的关系的散点图,下列结论中正确的是( )(变式)A. 人体脂肪含量与年龄正相关,且脂肪含量的中位数等于20%B. 人体脂肪含量与年龄正相关,且脂肪含量的中位数小于20%C. 人体脂肪含量与年龄负相关,且脂肪含量的中位数等于20%D. 人体脂肪含量与年龄负相关,且脂肪含量的中位数小于20%
【解析】 观察图形,可知人体脂肪含量与年龄正相关,且脂肪含量的中位数小于20%.
例2 对四组数据进行统计,获得如图所示的散点图,下列关于其样本相关系数的比较,正确的是( ) 图(1) 图(2) 图(3) 图(4)(例2)A. r2
例3 2016年起,某地区创新开展产业发展,响应第三产业的发展政策,经济收入逐年增加.该地的经济收入变化及构成比例如图所示.
2016年经济收入构成比例 2020年经济收入构成比例(例3)(1) 根据以上图表,试分析:与2016年相比,2020年第三产业与种植业收入的变化情况;
【解答】 ①与2016年相比,2020年第三产业的收入占比大幅度增加;2016年第三产业的收入为0.3百万元,2020年第三产业的收入为6百万元,收入大幅度增加.②与2016年相比,种植业收入占比减少,但种植业收入依然保持增长.
(2) 求经济收入y关于x的经验回归方程,并预测2025年该地区的经济收入.
求经验回归方程的步骤:
(2023·广东金太阳期初)2022年6月的某一周,某直播间的交易额共计3.5亿元,数据统计如下表.(1) 通过分析,发现可用线性回归模型拟合交易额y与天数t的关系,请用相关系数(系数精确到0.01)加以说明;
因为交易额y与t的相关系数近似为0.98,说明交易额y与t正线性相关,且相关强度很强,从而可用线性回归模型拟合交易额y与t的关系.
(2) 利用最小二乘法建立y关于t的经验回归方程(系数精确到0.1),并预测下一周第一天(即第8天)的交易额.
1. 已知变量x和y满足关系y=-0.1x+1,变量y与z正相关,则下列结论中正确的是( )A. x与y正相关,x与z负相关B. x与y正相关,x与z正相关C. x与y负相关,x与z负相关D. x与y负相关,x与z正相关
点击对应数字即可跳转到对应题目
【解析】 因为y=-0.1x+1的斜率小于0,故x与y负相关.
2. 某公司2016~2021年的年利润x(单位:百万元)与年广告支出y(单位:百万元)的统计资料如下表所示:根据统计资料,则利润的中位数( )A. 是16,x与y有正线性相关关系B. 是17,x与y有正线性相关关系C. 是17,x与y有负线性相关关系D. 是18,x与y有负线性相关关系
对于A,去除前变量x每增加1个单位,变量y大约增加2个单位,A错误;对于B,去除后剩余样本数据中x的平均数为2,B正确;对于D,去除了误差较大的样本数据后,线性相关性变强,因为y关于x正相关,则r>0,所以样本相关系数r变大,D正确.
2024年新高考数学第一轮复习课件:第46讲 第2课时 非线性回归模型与曲线拟合: 这是一份2024年新高考数学第一轮复习课件:第46讲 第2课时 非线性回归模型与曲线拟合,共23页。PPT课件主要包含了答案BC,e-2等内容,欢迎下载使用。
2024年新高考数学第一轮复习课件:第46讲 第1课时 变量的相关关系及线性回归模型: 这是一份2024年新高考数学第一轮复习课件:第46讲 第1课时 变量的相关关系及线性回归模型,共24页。PPT课件主要包含了答案C,答案D,答案ABC,答案乙数学等内容,欢迎下载使用。
2024年新高考数学第一轮复习课件:第17讲 第1课时 导数与不等关系: 这是一份2024年新高考数学第一轮复习课件:第17讲 第1课时 导数与不等关系,共17页。PPT课件主要包含了答案ACD,答案AC,-∞1,0+∞等内容,欢迎下载使用。












