数学七年级上册6.1 线段 射线 直线复习练习题

这是一份数学七年级上册6.1 线段 射线 直线复习练习题，文件包含专题61线段射线直线十大题型举一反三苏科版原卷版docx、专题61线段射线直线十大题型举一反三苏科版解析版docx等2份试卷配套教学资源，其中试卷共54页， 欢迎下载使用。


TOC \ "1-3" \h \u
\l "_Tc2468" 【题型1 线段、射线、直线概念辨析】 PAGEREF _Tc2468 \h 1
\l "_Tc14130" 【题型2 线段、射线、直线的区别与联系】 PAGEREF _Tc14130 \h 3
\l "_Tc25192" 【题型3 计数问题及其应用】 PAGEREF _Tc25192 \h 3
\l "_Tc23061" 【题型4 利用线段的和与差求线段长度】 PAGEREF _Tc23061 \h 4
\l "_Tc2132" 【题型5 线段中点的有关计算】 PAGEREF _Tc2132 \h 5
\l "_Tc31289" 【题型6 线段n等分点的有关计算】 PAGEREF _Tc31289 \h 6
\l "_Tc14671" 【题型7 线段的数量关系】 PAGEREF _Tc14671 \h 8
\l "_Tc23975" 【题型8 两点间的距离】 PAGEREF _Tc23975 \h 9
\l "_Tc11265" 【题型9 直线、线段的性质】 PAGEREF _Tc11265 \h 11
\l "_Tc11841" 【题型10 线段的长短比较及其应用】 PAGEREF _Tc11841 \h 12
【知识点1 线段、射线、直线】
【题型1 线段、射线、直线概念辨析】
【例1】（2022·河北保定·七年级期末）《红楼梦》第57回有这么一句话，“自古道:‘千里姻缘一线牵’,管姻缘的有一位月下老儿，暗里只用一根红线，把这两个人的脚绊住．”请问，这里所说的“线”若是真的，则在数学中指的应是（ ）
A．直线B．射线C．线段D．以上都不对
【变式1-1】（2022·全国·七年级课时练习）下列说法正确的是（ ）
A．直线AB和直线BA表示同一条直线B．过一点P只能作一条直线
C．射线AB和射线BA表示同一条射线D．射线a比直线b短
【变式1-2】（2022·河北邢台·七年级期中）若两个图形有公共点，则称这两个图形相交，否则称它们不相交．如图，直线PA、PB和线段AB将平面分成五个区域（不包含边界），若线段PQ与线段AB相交，则点Q落在的区域是（ ）
A．①B．②C．③D．④或⑤
【变式1-3】（2022·浙江宁波·七年级期末）如图，平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF，从射线OA开始按逆时针方向依次在射线上写出数字1，2，3，4，5，6，7，…则数字“2020”在（ ）
A．射线OA上B．射线OB上C．射线OD上D．射线OF上
【题型2 线段、射线、直线的区别与联系】
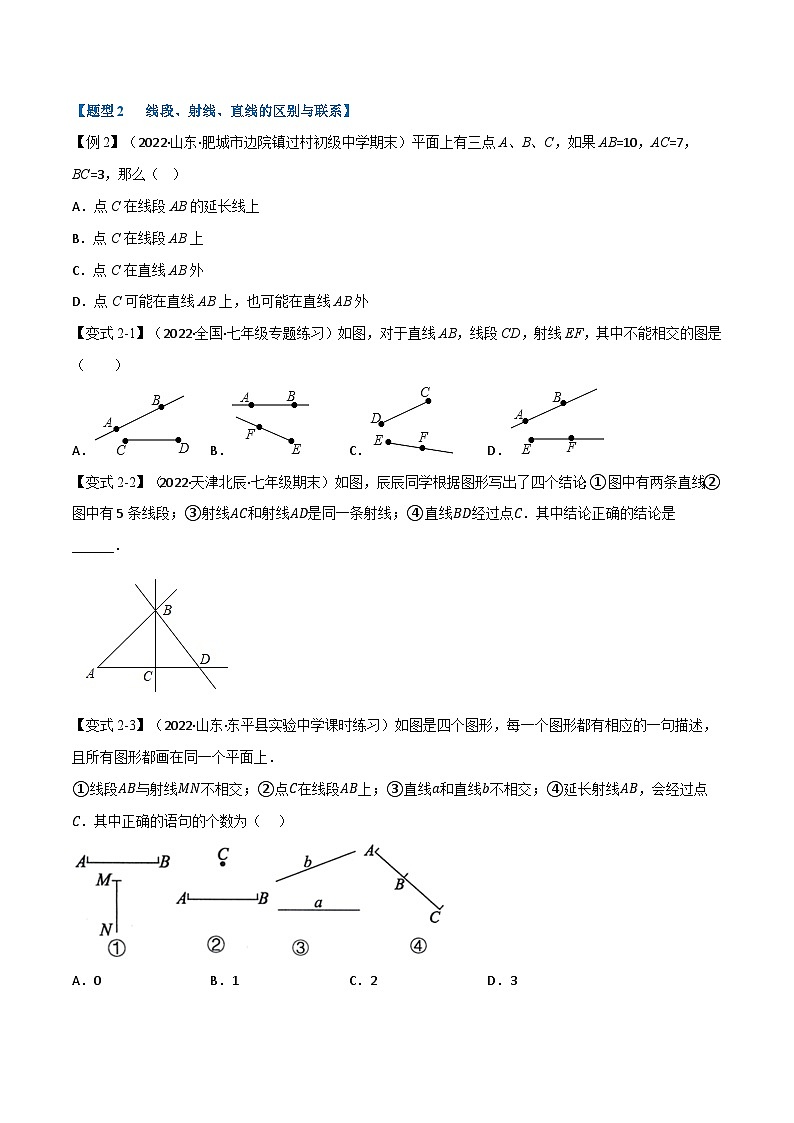
【例2】（2022·山东·肥城市边院镇过村初级中学期末）平面上有三点A、B、C，如果AB=10，AC=7，BC=3，那么（ ）
A．点C在线段AB的延长线上
B．点C在线段AB上
C．点C在直线AB外
D．点C可能在直线AB上，也可能在直线AB外
【变式2-1】（2022·全国·七年级专题练习）如图，对于直线AB，线段CD，射线EF，其中不能相交的图是（ ）
A．B．C．D．
【变式2-2】（2022·天津北辰·七年级期末）如图，辰辰同学根据图形写出了四个结论：①图中有两条直线；②图中有5条线段；③射线AC和射线AD是同一条射线；④直线BD经过点C．其中结论正确的结论是______．
【变式2-3】（2022·山东·东平县实验中学课时练习）如图是四个图形，每一个图形都有相应的一句描述，且所有图形都画在同一个平面上．
①线段AB与射线MN不相交；②点C在线段AB上；③直线a和直线b不相交；④延长射线AB，会经过点C．其中正确的语句的个数为（ ）
A．0B．1C．2D．3
【题型3 计数问题及其应用】
【例3】（2022·山东·泰安市泰山区大津口中学七年级阶段练习）如图是一段高铁行驶路线图，图中字母表示的5个点表示5个车站，在这段路线上往返行车，需印制________种车票（任何两站之间，往返两种车票），需要__________种不同的票价．
【变式3-1】（2022·湖南·长沙市开福区青竹湖湘一外国语学校九年级阶段练习）一只小虫子欲从A点不重复经过图中的点或者线段，而最终到达目的地E，这只小虫子的不同走法共有（ ）
A．12种B．13种C．14种D．15种
【变式3-2】（2022·全国·七年级课时练习）如图所示，图中过A点的直线共有________条，以A为端点的射线共有________条，以A为端点的线段共有________条．
【变式3-3】（2022·全国·七年级专题练习）若直线上有两个点，则以这两点为端点可以确定一条线段．请仔细观察图形，解决下列问题：
(1)如图1，直线l上有3个点A，B，C，则可以确定 条线段；
(2)如图2，直线l上有4个点A，B，C，D，则可以确定 条线段；
(3)若直线上有n个点，一共可以确定多少条线段？请写出解题过程．
【题型4 利用线段的和与差求线段长度】
【例4】（2022·北京朝阳·七年级期末）一种零件的图纸如图所示，若AB＝10mm，BC＝50mm，CD＝20mm，则AD的长为 _____mm．
【变式4-1】（2022·湖南湘西·七年级期末）如图，已知AD=65mm，BD=60mm，CD=15mm，求AB和BC的长．
【变式4-2】（2022·陕西宝鸡·七年级期末）如图，P是线段AB上一点，AB=12cm，M、N两点分别从P、B出发以1cms、3cms的速度同时向左运动（M在线段AP上，N在线段BP上），运动时间为ts．
（1）若M、N运动1s时，且PN=3AM，求AP的长；
（2）若M、N运动到任一时刻时，总有PN=3AM，AP的长度是否变化？若不变，请求出AP的长;若变化，请说明理由；
（3）在（2）的条件下，Q是直线AB上一点，且AQ=PQ+BQ，求PQ的长．
【变式4-3】（2022·广东广州·七年级期中）已知A，B，C，D四点在同一条直线上，点C是线段AB的中点．
(1)点D在线段AB上，且AB=6，BD=13BC，求线段CD的长度；
(2)若点E是线段AB上一点，且AE=2BE，当AD:BD=2:3时，线段CD与CE具有怎样的数量关系，请说明理由．
【知识点2 利用线段的中点求线段长度】
线段上的一个点把线段分成相等的两条线段，这个点叫做线段的中点.
【题型5 线段中点的有关计算】
【例5】（2022·重庆·西南大学附中七年级期末）如图，点D为线段AB的中点，点C为DB的中点，若AB=16，DE=13AE，则线段EC的长（ ）
A．7B．203C．6D．5
【变式5-1】（2022·江苏·沭阳县修远中学七年级阶段练习）已知点C是线段AB的中点，下列说法：①AB=2AC；②BC=12AB；③AC=BC；④AC+BC=AB．其中正确的个数是( )
A．1B．2C．3D．4
【变式5-2】（2022·江苏扬州·七年级期末）如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分，这点叫做这条折线的“折中点”．如图，点D是折线A﹣C﹣B的“折中点”，请解答以下问题：
(1)当AC＞BC时，点D在线段 上；当AC＝BC时，点D与 重合；当AC＜BC时，点D在线段 上；
(2)当AC＜BC时，若E为线段AC中点，EC＝8cm，CD＝6cm，求CB的长度．
【变式5-3】（2022·江苏·江阴市敔山湾实验学校七年级阶段练习）直线l上的三个点A、B、C，若满足BC＝12AB，则称点C是点A关于点B的“半距点”．如图1，BC＝12AB，此时点C就是点A关于点B的一个“半距点”．
若M、N、P三个点在同一条直线m上，且点P是点M关于点N的“半距点”，MN＝6cm．
(1)MP=_____cm
(2)若点G也是直线m上一点，且点G是线段MP的中点，求线段GN的长度．
【题型6 线段n等分点的有关计算】
【例6】（2022·湖南·郴州市明星学校七年级阶段练习）如图所示，C，D两点把线段AB分成了2：3：4三部分，M是AB的中点，DB＝12，求AM的长．
【变式6-1】（2022·江苏·鼓楼实验中学七年级阶段练习）定义：数轴上的三点，如果其中一个点与近点距离是它与远点距离的12，则称该点是其他两个点的“倍分点”．例如数轴上点A，B，C所表示的数分别为﹣1，0，2，满足AB＝12BC，此时点B是点A，C的“倍分点”．已知点A，B，C，M，N在数轴上所表示的数如图所示．
（1）A，B，C三点中，点 是点M，N的“倍分点”；
（2）若数轴上点M是点D，A的“倍分点”，则点D对应的数有 个，分别是 ；
（3）若数轴上点N是点P，M的“倍分点”，且点P在点N的右侧，求此时点P表示的数．
【变式6-2】（2022·全国·七年级专题练习）已知线段AB=15cm，点C在线段AB上，且AC:CB=3:2．
(1)求线段AC，CB的长；
(2)点P是线段AB上的动点且不与点A，B，C重合，线段AP的中点为M，设AP=mcm
①请用含有m的代数式表示线段PC，MC的长；
②若三个点M，P，C中恰有一点是其它两点所连线段的中点，则称M，P，C三点为“共谐点”，请直接写出使得M，P，C三点为“共谐点”的m的值．
【变式6-3】（2022·全国·七年级课时练习）小明在学习了比较线段的长短时对下面一道问题产生了探究的兴趣：
如图1，点C在线段AB上，M，N分别是AC，BC的中点．若AB＝12，AC＝8，求MN的长．
(1)根据题意，小明求得MN＝___________；
(2)小明在求解（1）的过程中，发现MN的长度具有一个特殊性质，于是他先将题中的条件一般化，并开始深入探究．
设AB＝a，C是线段AB上任意一点（不与点A，B重合），小明提出了如下三个问题，请你帮助小明解答．
①如图1，M，N分别是AC，BC的中点，则MN＝______________；
②如图2，M，N分别是AC，BC的三等分点，即AM=13AC，BN=13BC，求MN的长；
③若M，N分别是AC，BC的n等分点，即AM=1nAC，BN=1nBC，则MN＝___________；
【题型7 线段的数量关系】
【例7】（2022·江苏无锡·七年级期末）如图，C、D是线段AB上两点，且CD=3AD−2BC，则AC与BD的关系是（ ）
A．AC=BDB．2AC=BDC．3AC=2BDD．4AC=3BD
【变式7-1】（2022·全国·七年级课时练习）如图1，已知线段AB=20cm，点M是线段AB上一点，点C在线段AM上，点D在线段BM上，C、D两点分别从M、B出发以acm/s、bcm/s的速度沿直线BA运动，运动方向如箭头所示，其中a、b满足条件：|a−1|+|b−3|=0．
(1)直接写出：a=____________，b=_____________；
(2)若2cm(3)如图2，若AM=13AB，点N是直线AB上一点，且AN−BN=MN，求MN与AB的数量关系．
【变式7-2】（2022·全国·七年级课时练习）如图①、②所示，线段AB=20，线段CD=10，点E是BC的中点，设AC=a．
(1)当a=4时，则DE的长为______．
(2)在图①中，计算DE的长度（用含a的式子表示）
(3)将图①中的线段CD向右移动到图②的位置．
①直接写出线段AC与线段DE满足的数量关系．
②在线段AC上有点F，满足32AF+BE=12AC−AF，求AF的长度（用含a的式子表示）
【变式7-3】（2022·全国·七年级课时练习）某操作车间有一段直线型向左移动的传输带，A，B两位操作工人站于传输带同侧且相距16米，操作组长F也站在该侧，且到A，B距离相等，传输带上有一个8米长的工具筐CE．
(1)如图1，当CE位于A，B之间时，F发现工具筐的C端 离自己只有 1米，则工具筐C端离A 米，工具筐E端离B 米．
(2)工具筐C端从B点开始随传输带向左移动直至工具筐E端到达以A点为止，这期间工具筐E端到B的距离BE和工具筐E端到F的距离EF存在怎样的数量关系，并用等式表示，（你可以在图2中先画一画，再找找规律）
【知识点3 直线的性质】
经过两点有一条直线，并且只有一条直线.简单地：两点确定一条直线.
两条直线相交，只有一个交点.
【知识点4 线段的性质】
两点的所有连线中，线段最短。 简称：两点之间，线段最短。
连接两点间的线段的长度，叫做这两点的距离。
【题型8 两点间的距离】
【例8】（2022·全国·七年级专题练习）已知线段AB＝10cm，有下列说法：
①不存在到A，B两点的距离之和小于10cm的点；
②线段AB上存在无数个到A，B两点的距离之和等于10cm的点；
③线段AB外存在无数个到A，B两点的距离之和大于10cm 的点．
其中正确的是（ ）
A．①②B．①③C．②③D．①②③
【变式8-1】（2022·河北石家庄·七年级期末）如图，A、B、C、D表示四个车站的位置，A、B两站之间的距离AB=a−b，B、C两站之间的距离BC=2a−b，B、D两站之间的距离BD=72a−2b−1．
(1)求C，D两站之间的距离CD（用含a，b的式子表示）；
(2)当A，C两站之间的距离AC=90km时，求C、D两站之间的距离CD．
【变式8-2】（2022·全国·七年级课时练习）如图所示，M是线段AB上一定点，AB=12cm，C，D两点分别从点M，B出发以1cm/s，2cm/s的速度沿直线BA向左运动，运动方向如箭头所示（点C在线段AM上，点D在线段BM上）．
（1）当点C，D运动了2s时，求AC+MD的值．
（2）若点C，D运时，总有MD=2AC，则AM=_______．
（3）在（2）的条件下，N是直线AB上一点，且AN−BN=MN，求MNAB的值．
【变式8-3】（2022·江苏淮安·七年级期末）【探索新知】
如图1，点C在线段AB上，图中共有3条线段：AB、AC和BC，若其中有一条线段的长度是另一条线段长度的两倍，则称点C是线段AB的“二倍点”.
（1）①一条线段的中点 这条线段的“二倍点”；（填“是”或“不是”）
②若线段AB=20，C是线段AB的“二倍点”，则BC= （写出所有结果）
【深入研究】
如图2，若线段AB=20cm，点M从点B的位置开始，以每秒2cm的速度向点A运动，当点M到达点A时停止运动，运动的时间为t秒.
（2）问t为何值时，点M是线段AB的“二倍点”；
（3）同时点N从点A的位置开始，以每秒1cm的速度向点B运动，并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.
【题型9 直线、线段的性质】
【例9】（2022·全国·七年级课时练习）下列现象：
①用两个钉子就可以把木条固定在墙上
②从A地到B地架设电线，总是尽可能沿着线段AB架设
③植树时，只要确定两棵树的位置，就能确定同一行树所在的直线
④把弯曲的公路改直，就能缩短路程
其中能用“两点之间线段最短”来解释的现象有（ ）
A．①④B．①③C．②④D．③④
【变式9-1】（2022·河南·郑州市第四初级中学七年级期末）值日生小明想把教室桌椅摆放整齐，为了将一列课桌对齐，他把这列课桌的最前面一张和最后面一张先拉成一条线，其余课桌按这条直线摆放，这样做用到的数学知识是__________．
【变式9-2】（2022·浙江绍兴·七年级期末）如图，在方格纸中，点A，B，C，D，E，F，H，K中，在同一直线上的三个点有（ ）．
A．3组B．4组C．5组D．6组
【变式9-3】（2022·广东汕尾·七年级期末）如图，点C在∠AOB的边OA上，选择合适的画图工具按要求画图．，
（1）反向延长射线OB，得到射线OD，在射线OD上取一点F，使得OF=OC；
（2）使用量角器，画出∠AOD的角平分线OE；
（3）在射线OE上作一点P，使得CP+FP最小；
（4）写出你完成（3）的作图依据：______．
【题型10 线段的长短比较及其应用】
【例10】（2022·江苏·无锡市华庄中学七年级期中）如图，在公路MN两侧分别有A1,A2,···,A7，七个工厂，各工厂与公路MN（图中粗线）之间有小公路连接．现在需要在公路MN上设置一个车站，选择站址的标准是“使各工厂到车站的距离之和越小越好”．则下面结论中正确的是（ ）
①车站的位置设在C点好于B点；
②车站的位置设在B点与C点之间公路上任何一点效果一样；
③车站位置的设置与各段小公路的长度无关；
④车站的位置设在BC段公路的最中间处要好于设在点B及点C处．
A．①③B．③④C．②③D．②
【变式10-1】（2022·全国·七年级课时练习）在标枪训练课上，小秦在点O处进行了四次标枪试投，若标枪分别落在图中M,N,P,Q的四个点处，则表示他最好成绩的点是（ ）
A．MB．P
C．ND．Q
【变式10-2】（2022·重庆巫山·七年级期末）如图所示，某乡镇A、B、C、D、E五个村庄位于同一条笔直的公路边，相邻两个村庄的距离分别为AB＝1千米，BC＝3千米，CD＝2千米，DE＝1.5千米．乡村扶贫改造期间，该乡镇打算在此间新建一个便民服务点M，使得五个村庄到便民服务点的距离之和最小，则这个最小值为_________千米．
【变式10-3】（2022·全国·七年级课时练习）如图所示，某公司有三个住宅区，A、B、C各区分别住有职工30人，15人，10人，且这三点在一条大道上（A，B，C三点共线），已知AB＝100米，BC＝200米．为了方便职工上下班，该公司的接送车打算在此间只设一个停靠点，为使所有的人步行到停靠点的路程之和最小，那么该停靠点的位置应设在（ ）
A．点AB．点BC．A，B之间D．B，C之间 名称
直线
射线
线段
图形
B
A
A
B
B
A
端点个数
无
一个
两个
表示法
直线
直线AB（BA）
射线
射线AB
线段
线段AB（BA）
作法叙述
作直线
作直线AB
作射线
作射线AB
作线段
作线段AB
连接AB
延长
向两端无限延长
向一端无限延长
不可延长