2022-2023学年河北省承德市平泉市八年级（下）期末数学试卷（含解析）

2022-2023学年河北省承德市平泉市八年级（下）期末数学试卷

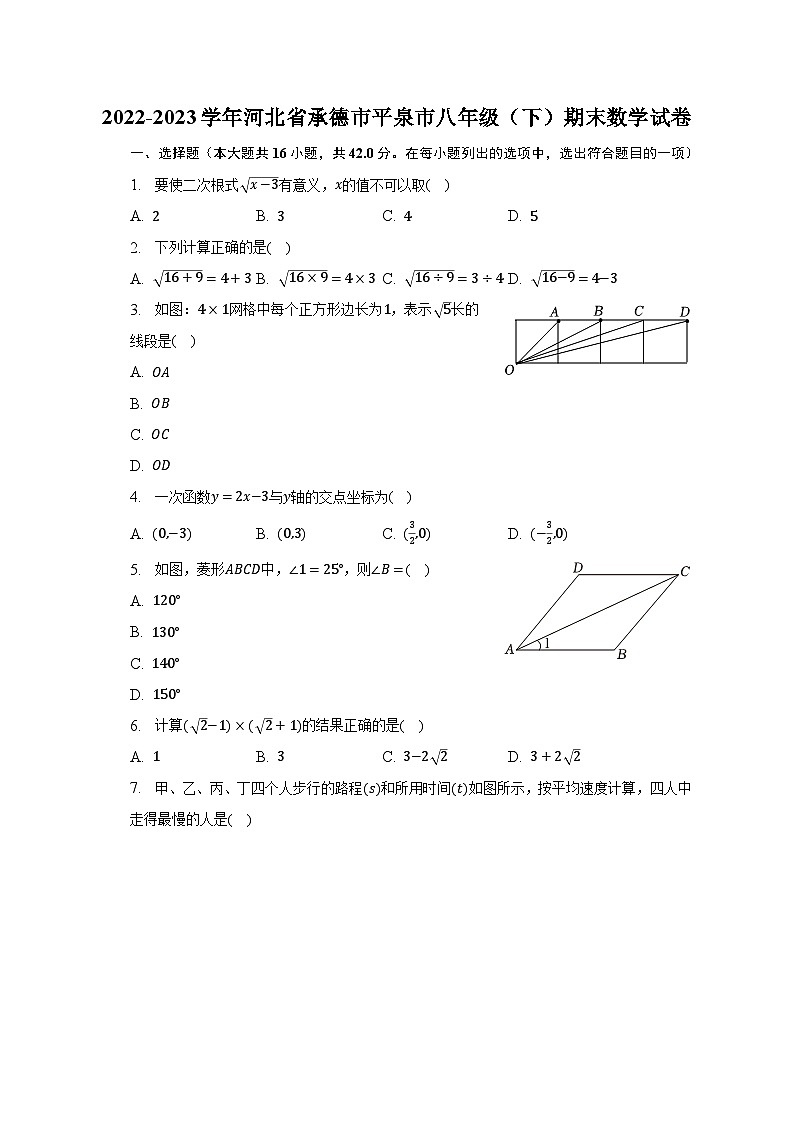
一、选择题（本大题共16小题，共42.0分。在每小题列出的选项中，选出符合题目的一项）

1.  要使二次根式有意义，的值不可以取(    )

A.  B.  C.  D.

2.  下列计算正确的是(    )

A.  B.  C.  D.

3.  如图：网格中每个正方形边长为，表示长的线段是(    )

A.
B.
C.
D.

4.  一次函数与轴的交点坐标为(    )

A.  B.  C.  D.

5.  如图，菱形中，，则(    )

A.
B.
C.
D.

6.  计算的结果正确的是(    )

A.  B.  C.  D.

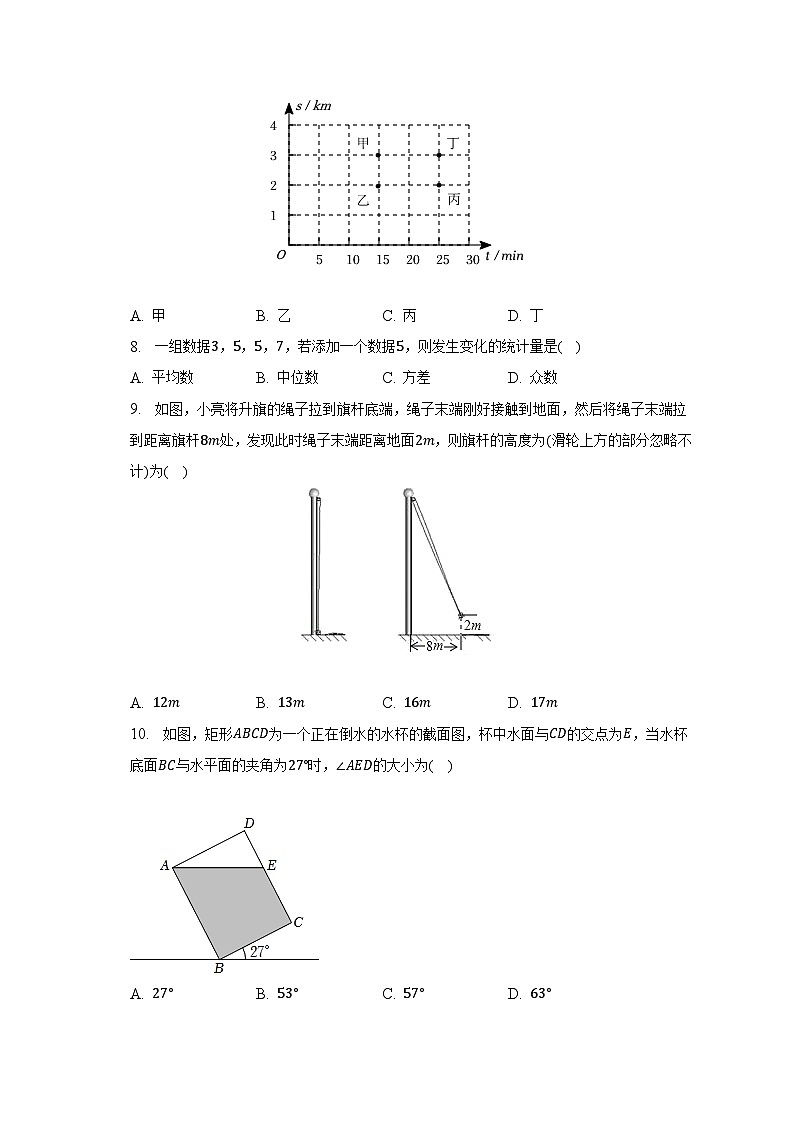
7.  甲、乙、丙、丁四个人步行的路程和所用时间如图所示，按平均速度计算，四人中走得最慢的人是(    )

A. 甲 B. 乙 C. 丙 D. 丁

8.  一组数据，，，，若添加一个数据，则发生变化的统计量是(    )

A. 平均数 B. 中位数 C. 方差 D. 众数

9.  如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆处，发现此时绳子末端距离地面，则旗杆的高度为滑轮上方的部分忽略不计为(    )

A.  B.  C.  D.

10.  如图，矩形为一个正在倒水的水杯的截面图，杯中水面与的交点为，当水杯底面与水平面的夹角为时，的大小为(    )

 

A.  B.  C.  D.

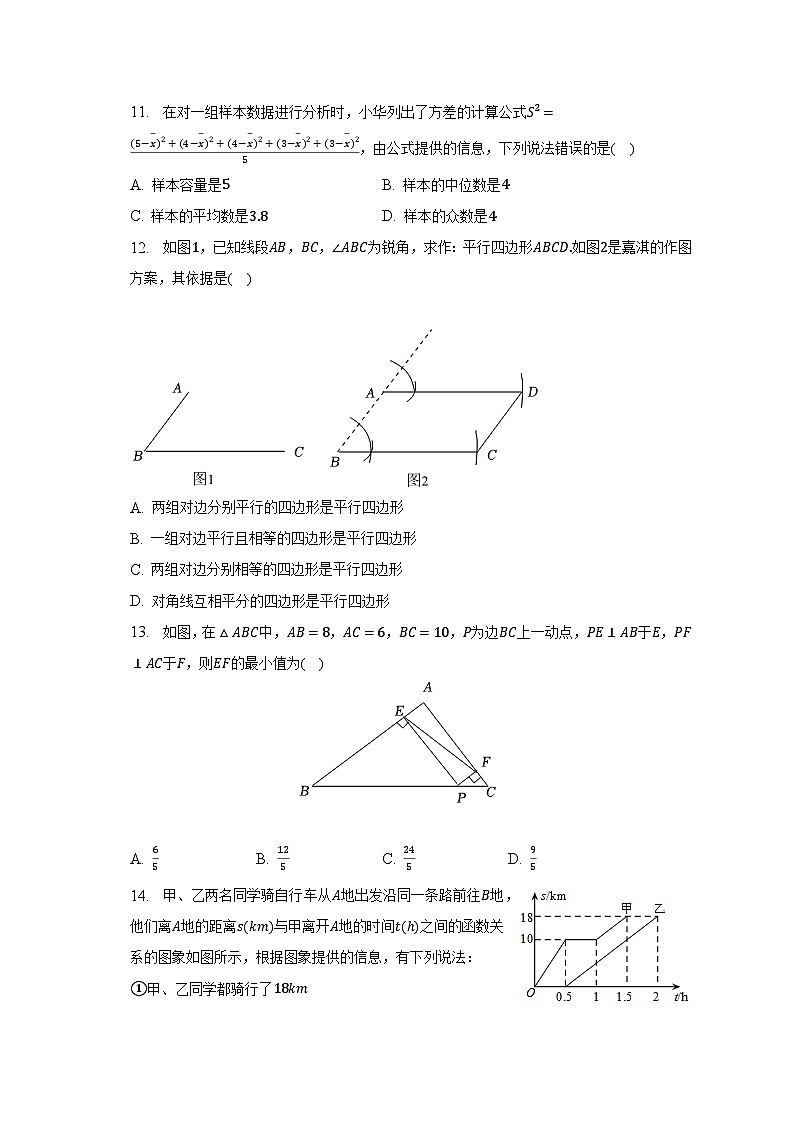
11.  在对一组样本数据进行分析时，小华列出了方差的计算公式，由公式提供的信息，下列说法错误的是(    )

A. 样本容量是 B. 样本的中位数是
C. 样本的平均数是 D. 样本的众数是

12.  如图，已知线段，，为锐角，求作：平行四边形如图是嘉淇的作图方案，其依据是(    )

 

A. 两组对边分别平行的四边形是平行四边形
B. 一组对边平行且相等的四边形是平行四边形
C. 两组对边分别相等的四边形是平行四边形
D. 对角线互相平分的四边形是平行四边形

13.  如图，在中，，，，为边上一动点，于，于，则的最小值为(    )

A.  B.  C.  D.

14.  甲、乙两名同学骑自行车从地出发沿同一条路前往地，他们离地的距离与甲离开地的时间之间的函数关系的图象如图所示，根据图象提供的信息，有下列说法：
甲、乙同学都骑行了
甲、乙同学同时到达地
甲停留前、后的骑行速度相同
乙的骑行速度是
其中正确的说法是(    )

A.  B.  C.  D.

15.  如图，将两张宽度相同的矩形纸条交叉叠放小明发现重叠部分四边形是菱形，并进行如下所示的推理．

小芳认为小明的推理不严谨，她认为应在“”和“四边形是菱形”之间作补充下列说法正确的是(    )

A. 应补充：，
B. 小明的推理严谨，不必补充
C. 应补充：
D. 应补充：

16.  如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案．现有五种正方形纸片，面积分别是，，，，，选取其中三块可重复选取按图的方式组成图案，使所围成的三角形是面积最大的直角三角形，则选取的三块纸片的面积分别是(    )

A. ，，
B. ，，
C. ，，
D. ，，

二、填空题（本大题共3小题，共9.0分）

17.  化简______．

18.  大正方形边长为，小正方形边长为．
是否为直角三角形？______ 填“是”或“否”
大正方形与小正方形的面积之差是，求阴影部分的面积为______ ．

19.  如图，直线：与直线：交于点，直线：过定点．

点坐标______ ．
若直线：经过点， ______ ．
直线：经过点时，不能与直线、围成三角形，再写出另外两个值，使得、、三条直线围不成三角形， ______ ．

三、解答题（本大题共7小题，共69.0分。解答应写出文字说明，证明过程或演算步骤）

20.  本小题分
若，．
求值；
求值．

21.  本小题分
如图，在矩形中，，，翻折，使点落在对角线上处．
______ ；是的______ 中线、角平分线、高线；
求和的长．

22.  本小题分
某校学生会要在甲、乙两位候选人中选择一人担任文艺部干事，对他们进行了文化水平、艺术水平、组织能力的测试，根据综合成绩择优录取，他们的各项成绩如表所示：

如果把各项成绩的平均数作为综合成绩，应该录取谁？
如果想录取一名组织能力较强的候选人，把文化水平、艺术水平、组织能力三项成绩分别按照：：的比例计入综合成绩，应该录取谁？

23.  本小题分
某商店用调低价格的方式促销个不同的玩具，调整后的单价元与调整前的单价元满足一次函数关系，如表：

已知这个玩具调整后的单价都大于元．
求与的函数关系式，并确定的取值范围；
某个玩具调整前单价是元，顾客购买这个玩具省了多少钱？

24.  本小题分
如图，，为中点，点为射线上不与点重合的任意一点，连接，并使的延长线交射线于点，连接，，设．

求证：四边形是平行四边形；
当四边形是矩形时，求的度数．

25.  本小题分
直线：与直线交于点，且直线过点．
求值；
求直线解析式；
点，同时在直线和上，直接写出值．

26.  本小题分
如图，正方形的边长为，为中点，过顶点作直线与边交于点点不与、重合，分别过点，作直线的垂线，垂足分别为点，．

______ ；
求证：≌；
计算： ______ ；
连接，当位置变化时，的长度是否变化？
当位置变化时，的长度随之变化，请直接写出长度的最小值．

答案和解析

1.【答案】 

【解析】解：要使二次根式有意义，
则，
解得：，
故的值不可以取．
故选：．
直接利用二次根式有意义的条件进而得出答案．
此题主要考查了二次根式有意义的条件，正确把握二次根式的定义是解题关键．
 

2.【答案】 

【解析】解： ，故该选项错误；
B. ，故该选项正确；
C. ，故该选项错误；
D. ，故该选项错误；
故选：．
根据算术平方根的定义和性质计算即可．
本题主要考查算术平方根的运算，先算根号下的结果，再开根号是解题的关键．
 

3.【答案】 

【解析】解：由勾股定理得，
，
，
，
表示应为线段．
故选：．
利用勾股定理求出每条线段的长，再进行判断即可．
本题考查的是勾股定理，掌握利用勾股定理求线段的长是解题关键．
 

4.【答案】 

【解析】解：
在中，令可得，
与轴的交点坐标为，
故选：．
令可求得的值，则可求得答案．
本题主要考查函数图象与坐标轴的交点，掌握函数图象与坐标轴交点的求法是解题的关键．
 

5.【答案】 

【解析】解：四边形是菱形，，
，，
，
故选B．
根据菱形的对角线平分一组对角求出，再由平行线的性质即可得到答案．
本题主要考查了菱形的性质，熟知菱形的性质是解题的关键．
 

6.【答案】 

【解析】解：


，
故选：．
根据平方差公式计算即可．
本题考查二次根式的混合运算，熟练掌握运算法则是解答本题的关键．
 

7.【答案】 

【解析】解：分钟甲比乙步行的路程多，分钟丁比丙步行的路程多，
甲的平均速度乙的平均速度，丁的平均速度丙的平均速度，
步行千米时，乙比丙用的时间少，
乙的平均速度丙的平均速度，
四人中走得最慢的人是丙，
故选：．
当时间一样的时候，分别比较甲、乙和丙、丁的平均速度；当路程都是千米的时候，比较甲、丁的平均速度即可得出答案．
本题考查了函数的图象，通过控制变量法比较平均速度的大小是解题的关键．
 

8.【答案】 

【解析】解：原数据的，，，的平均数为，
中位数为，
众数为，
方差为；
新数据，，，，的平均数为，
中位数为，
众数为，
方差为；
所以添加一个数据，方差发生变化，
故选：．
依据的定义和公式分别计算新旧两组数据的平均数、中位数、众数、方差求解即可．
本题主要考查的是众数、中位数、方差、平均数，熟练掌握相关概念和公式是解题的关键．
 

9.【答案】 

【解析】解：如图，过点作，设旗杆高度为，则，，，
在中，，即，
解得：，
即旗杆的高度为米．
故选：．
根据题意画出示意图，设旗杆高度为，可得，，，在中利用勾股定理可求出．
本题考查了勾股定理的应用，解答本题的关键是构造直角三角形，构造直角三角形的一般方法就是作垂线．
 

10.【答案】 

【解析】解：

，
，
四边形是矩形，
，，
，
，
，
，
．
故选：．
根据题意可知，，，等量代换求出，再根据平行线的性质求出．
本题考查了矩形的性质，熟记矩形的性质并灵活运用是解题的关键．
 

11.【答案】 

【解析】解：由方差的计算公式知，这组数据为、、、、，
所以这组数据的样本容量为，中位数为，众数为和，平均数为，
故选：．
由方差的计算公式得出这组数据为、、、、，再根据中位数、众数和平均数的定义求解即可．
本题主要考查方差，解题的关键是根据方差的计算公式得出样本的具体数据及中位数、众数和平均数的定义．
 

12.【答案】 

【解析】解：由作图过程可知：先作同位角，可得；再作，所以依据是一组对边平行且相等的四边形是平行四边形．
故选：．

根据作图过程进行分析即可解答．
本题主要考查了平行四边形的判定、尺规作图等知识点，理解尺规作图所隐含的条件是解答本题的关键．
 

13.【答案】 

【解析】解：连接，
如图所示，

，，．
，，
，则是直角三角形，且．
，．
四边形是矩形，
，
当时，取得最小值，即取得最小值，
．
故选：．
连接，勾股定理的逆定理证明是直角三角形，且，进而得出四边形是矩形，则，然后根据等面积法即可求解．
本题考查了勾股定理的逆定理，矩形的性质，垂线段最短，熟练掌握以上知识是解题的关键．
 

14.【答案】 

【解析】解：由图象可得，
甲、乙同学都骑行了，故正确，
甲比乙先到达地，故错误，
甲停留前的速度为：，甲停留后的速度为：，故错误，
乙的骑行速度为：，故正确，
故选：．
根据题意和函数图象中的数据可以判断各个小题中的结论是否正确，从而可以解答本题．
本题考查函数图象，解答本题的关键是明确题意，利用数形结合的思想解答．
 

15.【答案】 

【解析】解：如图，过点分别作，的垂线，垂足分别为点，，则．
，，
四边形是平行四边形．
，，
，
四边形是菱形．
故选：．
根据一组邻边相等的平行四边形是菱形即可解决问题．
本题考查菱形的判定与性质，矩形的性质，平行四边形的判定与性质，解决本题的关键是掌握菱形的判定与性质．
 

16.【答案】 

【解析】解：由题可知每个正方形纸片的面积正好是围成三角形的对应边的边长的平方，
当选取的三块纸片的面积分别是，，时，因为，所以围成的三角形是直角三角形，其面积是，
当选取的三块纸片的面积分别是，，时，因为，所以围成的三角形是直角三角形，其面积是；
当选取的三块纸片的面积分别是，，时，因为，所以围成的三角形不是直角三角形，不符合题意；
当选取的三块纸片的面积分别是，，时，因为，所以围成的三角形是直角三角形，其面积是，
因为，
所以使所围成的三角形是面积最大的直角三角形时选取的三块纸片的面积分别是，，，
故选：．
首先根据两个较小的面积之和等于最大的面积判断三角形是直角三角形，然后利用较小的两条边为直角边，根据三角形的面积公式分别计算出各个选项中围成的直角三角形的面积，比较大小即可解答本题．
本题考查勾股定理的逆定理，解答本题的关键是明确题意，利用勾股定理的逆定理解答．
 

17.【答案】 

【解析】解：原式．
故答案为：．
先计算出被开方数的值，再求出其算术平方根即可．
本题考查的是算术平方根的概念，即一般地，如果一个正数的平方等于，即，那么这个正数叫做的算术平方根．
 

18.【答案】否   

【解析】解：四边形，四边形是正方形，
，
，，且
，
不是直角三角形，
阴影部分的面积是：




故答案为：否；．
根据正方形的性质得出，再根据，，即可得出，进而得出不是直角三角形；阴影部分的面积是：，推出，进而得出答案．
此题主要考查了整式的混合运算，正方形的性质，关键是正确运用算式表示出阴影部分面积．
 

19.【答案】   或 

【解析】解：：，
，
当时，，
：过定点的坐标为．
故答案为．
将点代入解析式：，
，
解得：．
故答案为．
使得、、三条直线围不成三角形
或，
当时，；
当时，；
综上，或．
故答案为或．
将解析式：变为即可解答；
将点代入解析式：，再解关于的方程即可；
分或两种情况，分别根据平行线的解析式的特点即可解答．
本题主要考查了一次函数的性质、待定系数法求函数解析式、平行线的解析式的特点等知识点，掌握平行线解析式的一次项系数相同．
 

20.【答案】解：


；



． 

【解析】根据平方差公式求解即可；
根据二次根式的加减先算括号内的，再算乘法．
本题考查二次根式的混合运算，平方差公式，正确计算是解题的关键．
 

21.【答案】  角平分线 

【解析】解：四边形为矩形，
，
，，
在中，，
翻折，使点落在对角线上处，
，
是的角平分线，
故答案为：，角平分线；
由折叠知：，，
，
设，在中，运用勾股定理得：，
解得：，
即：．
根据勾股定理可求得，由翻折可得，于是可得是的角平分线；
由折叠知：，，从而可求得，再利用勾股定理即可求解．
本题考查了矩形的性质、勾股定理以及折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了矩形的性质．
 

22.【答案】解：甲的综合成绩为分，
乙的综合成绩为分，
因为乙的综合成绩比甲的高，所以应该录取乙．
甲的综合成绩为分，
乙的综合成绩为分，
因为甲的综合成绩比乙的高，所以应该录取甲． 

【解析】分别求出甲、乙的算术平均数，然后比较即可解答；
分别求出甲、乙的加权平均数，然后比较即可解答．
本题主要考查了算术平均数、加权平均数等知识点，掌握算术平均数和加权平均数的区别是解答本题的关键．
 

23.【答案】解：设，由题意得，，，，

解得，
与的函数关系式为，
这个玩具调整后的单价都大于元，
，解得，
的取值范围是；

将代入得，
，
答：顾客购买这个玩具省了元； 

【解析】设，根据题意列方程组即可得到结论，再根据已知条件得到不等式于是得到的取值范围是；
将代入即可得到结论；
本题考查了一次函数的应用，求函数的解析式，熟记一次函数的性质是解题的关键．
 

24.【答案】证明：，
，
为中点，
，
，
≌，
，
四边形是平行四边形；
解：四边形是矩形，
，
，
是等腰三角形，
，
在中，，
即． 

【解析】根据平行线的判定可知，再根据全等三角形的判定与性质可知，最后根据平行四边形的判定即可解答；
根据矩形的性质可知是等腰三角形，再根据等腰三角形的性质解答即可．
本题考查了平行线的判定与性质，平行四边形的判定与性质，矩形的性质，等腰三角形的性质，三角形的内角和，掌握平行四边形的判定与性质是解题的关键．
 

25.【答案】解：把代入，得，
解得；
设直线解析式设，
把，代入得：
，
解得：，
；
解：点，，
，
依题意得，
解得． 

【解析】把点的坐标代入直线的解析式求出的值，即可得解；
根据点、的坐标，利用待定系数法求一次函数解析式即可；
根据，列式计算解答即可．
本题考查了两直线相交的问题，直线与坐标轴的交点，待定系数法求一次函数解析式，是基础知识，一定要熟练掌握并灵活运用．
 

26.【答案】   

【解析】解：正方形的边长为，为中点，
，，，
，
故答案为：；
证明：四边形为正方形，
，，
，，
，
，
，
≌；
解：≌，
，
在中，由勾股定理得，
，
故答案为：；
解：当位置变化时，的长度不发生变化为定值，理由如下：
，
，
，为的中点，
，
当位置变化时，的长度不发生变化为定值；

如图所示，连接，
，
，
长度的最小值为，此时、、三点共线．

根据正方形的性质和线段中点的定义得到，，，再利用勾股定理求出答案即可；
先由正方形的性质得到，，再由垂直的定义和三角形内角和定理证明，，即可证明≌；
由全等三角形的性质得到，则由勾股定理可得；
根据直角三角形斜边上的中线等于斜边的一半进行求解即可；
如图所示，连接，根据进行求解即可．
本题主要考查了正方形的性质，全等三角形的性质与判定，勾股定理，三角形三边的关系，直角三角形的性质等等，灵活运用所学知识是解题的关键．