2023年江苏省南通市中考数学试卷（含解析）

这是一份2023年江苏省南通市中考数学试卷（含解析），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2023年江苏省南通市中考数学试卷
一、选择题（本大题共10小题，每小题3分，共30分。在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）
1．（3分）计算（﹣3）×2，正确的结果是（　　）
A．6 B．5 C．﹣5 D．﹣6
2．（3分）2023年5月21日，以“聚力新南通、奋进新时代”为主题的第五届通商大会暨全市民营经济发展大会召开，40个重大项目集中签约，计划总投资约41800000000元，将41800000000用科学记数法表示为（　　）
A．4.18×1011 B．4.18×1010 C．0.418×1011 D．418×108
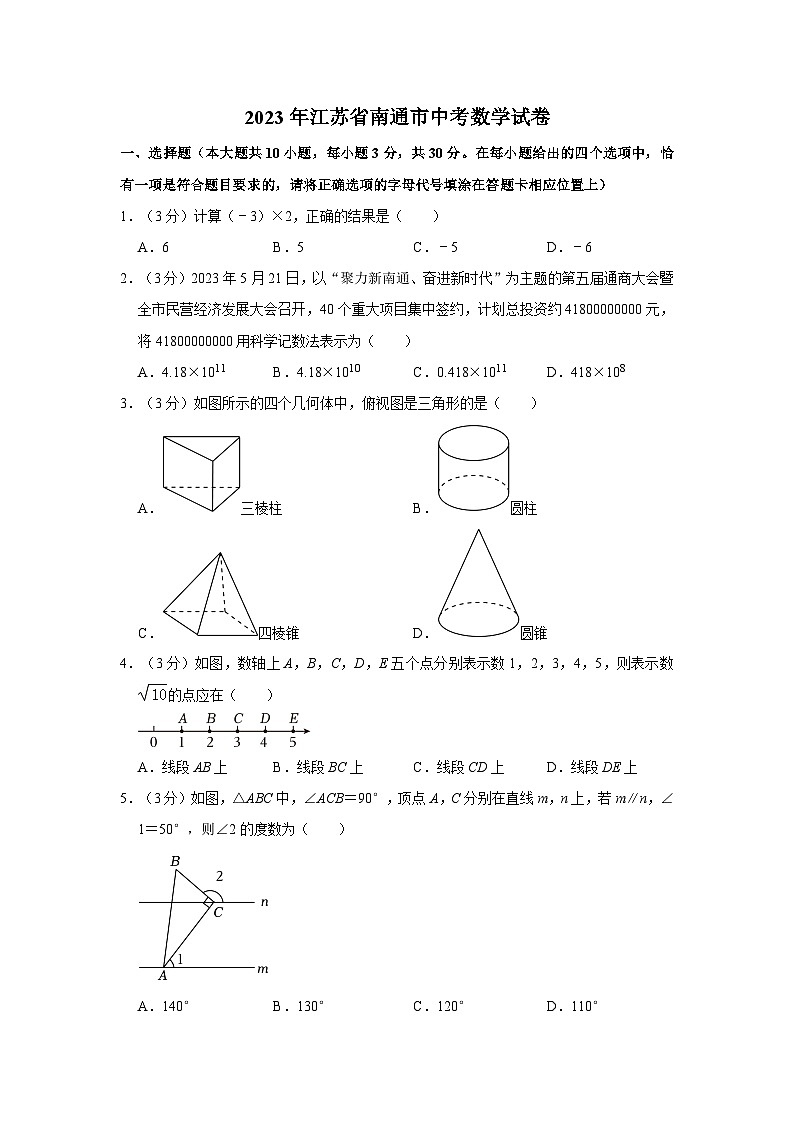
3．（3分）如图所示的四个几何体中，俯视图是三角形的是（　　）
A．三棱柱 B．圆柱
C．四棱锥 D．圆锥
4．（3分）如图，数轴上A，B，C，D，E五个点分别表示数1，2，3，4，5，则表示数 的点应在（　　）

A．线段AB上 B．线段BC上 C．线段CD上 D．线段DE上
5．（3分）如图，△ABC中，∠ACB＝90°，顶点A，C分别在直线m，n上，若m∥n，∠1＝50°，则∠2的度数为（　　）

A．140° B．130° C．120° D．110°
6．（3分）若a2﹣4a﹣12＝0，则2a2﹣8a﹣8的值为（　　）
A．24 B．20 C．18 D．16
7．（3分）如图，从航拍无人机A看一栋楼顶部B的仰角α为30°，看这栋楼底部C的俯角β为60°，无人机与楼的水平距离为120m，则这栋楼的高度为（　　）

A． B． C． D．
8．（3分）如图，四边形ABCD是矩形，分别以点B，D为圆心，线段BC，DC长为半径画弧，两弧相交于点E，连接BE，DE，BD．若AB＝4，BC＝8，则∠ABE的正切值为（　　）

A． B． C． D．
9．（3分）如图1，△ABC中，∠C＝90°，AC＝15，BC＝20．点D从点A出发沿折线A﹣C﹣B运动到点B停止，过点D作DE⊥AB，垂足为E．设点D运动的路径长为x，△BDE的面积为y，若y与x的对应关系如图2所示，则a﹣b的值为（　　）
​
A．54 B．52 C．50 D．48
10．（3分）若实数x，y，m满足x+y+m＝6，3x﹣y+m＝4，则代数式﹣2xy+1的值可以是（　　）
A．3 B． C．2 D．
二、填空题（本大题共8小题，第11～12题每小题3分，第13～18题每小题3分，共30分，不需写出解答过程，请把答案直接填写在答题卡相应位置上）
11．（3分）计算＝　 　．
12．（3分）分解因式：a2﹣ab＝　 　．
13．（4分）如图，△ABC中，D，E分别是AB，AC的中点，连接DE，则＝　 　．
​

14．（4分）某型号汽车行驶时功率一定，行驶速度v（单位：m/s）与所受阻力F（单位：N）是反比例函数关系，其图象如图所示．若该型号汽车在某段公路上行驶时速度为30m/s，则所受阻力F为 　 　N．

15．（4分）如图，AB是⊙O的直径，点C，D在⊙O上，若∠DAB＝66°，则∠ACD＝　 　度．

16．（4分）勾股数是指能成为直角三角形三条边长的三个正整数，世界上第一次给出勾股数公式的是中国古代数学著作《九章算术》．现有勾股数a，b，c，其中a，b均小于c，a＝m2﹣，，m是大于1的奇数，则b＝　 　（用含m的式子表示）．
17．（4分）已知一次函数y＝x﹣k，若对于x＜3范围内任意自变量x的值，其对应的函数值y都小于2k，则k的取值范围是 　 　．
18．（4分）如图，四边形ABCD的两条对角线AC，BD互相垂直，AC＝4，BD＝6，则AD+BC的最小值是 　 　．

三、解答题（本大题共8小题，共90分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．（12分）（1）解方程组：；
（2）计算：．
20．（10分）某校开展以“筑梦天宫、探秘苍穹”为主题的航天知识竞赛，赛后在七、八年级各随机抽取20名学生的竞赛成绩，进行整理、分析，得出有关统计图表．
抽取的学生竞赛成绩统计表
年级
平均数
中位数
众数
方差
七年级
82
83
87
52.6
八年级
82
84
91
65.6

注：设竞赛成绩为x（分），规定：
90≤x≤100为优秀；75≤x＜90为良好；
60≤x＜75为合格；x＜60为不合格．
（1）若该校八年级共有300名学生参赛，估计优秀等次的约有 　 　人；
（2）你认为七、八年级中哪个年级学生的竞赛成绩更好些？请从两个方面说明理由．

21．（10分）如图，点D，E分别在AB，AC上，∠ADC＝∠AEB＝90°，BE，CD相交于点O，OB＝OC．
求证：∠1＝∠2．
小虎同学的证明过程如下：
证明：∵∠ADC＝∠AEB＝90°，
∴∠DOB+∠B＝∠EOC+∠C＝90°．
∵∠DOB＝∠EOC，
∴∠B＝∠C．……第一步
又OA＝OA，OB＝OC，
∴△ABO≌△ACO．……第二步
∴∠1＝∠2．……第三步
（1）小虎同学的证明过程中，第 　 　步出现错误；
（2）请写出正确的证明过程．

22．（10分）有同型号的A，B两把锁和同型号的a，b，c三把钥匙，其中a钥匙只能打开A锁，b钥匙只能打开B锁，c钥匙不能打开这两把锁．
（1）从三把钥匙中随机取出一把钥匙，取出c钥匙的概率等于 　 　；
（2）从两把锁中随机取出一把锁，从三把钥匙中随机取出一把钥匙，求取出的钥匙恰好能打开取出的锁的概率．
23．（10分）如图，等腰三角形OAB的顶角∠AOB＝120°，⊙O和底边AB相切于点C，并与两腰OA，OB分别相交于D，E两点，连接CD，CE．
（1）求证：四边形ODCE是菱形；
（2）若⊙O的半径为2，求图中阴影部分的面积．

24．（12分）为推进全民健身设施建设，某体育中心准备改扩建一块运动场地．现有甲、乙两个工程队参与施工，具体信息如下：
信息一
工程队
每天施工面积（单位：m2）
每天施工费用（单位：元）
甲
x+300
3600
乙
x
2200
信息二
甲工程队施工1800m2所需天数与乙工程队施工1200m2所需天数相等．
（1）求x的值；
（2）该工程计划先由甲工程队单独施工若干天，再由乙工程队单独继续施工，两队共施工22天，且完成的施工面积不少于15000m2．该段时间内体育中心至少需要支付多少施工费用？
25．（13分）正方形ABCD中，点E在边BC，CD上运动（不与正方形顶点重合）．作射线AE，将射线AE绕点A逆时针旋转45°，交射线CD于点F．
​
（1）如图，点E在边BC上，BE＝DF，则图中与线段AE相等的线段是 　 　；
（2）过点E作EG⊥AF，垂足为G，连接DG，求∠GDC的度数；
（3）在（2）的条件下，当点F在边CD延长线上且DF＝DG时，求的值．
26．（13分）定义：平面直角坐标系xOy中，点P（a，b），点Q（c，d），若c＝ka，d＝﹣kb，其中k为常数，且k≠0，则称点Q是点P的“k级变换点”．例如，点（﹣4，6）是点（2，3）的“﹣2级变换点”．
（1）函数y＝﹣的图象上是否存在点（1，2）的“k级变换点”？若存在，求出k的值；若不存在，说明理由；
（2）点A（t，t﹣2）与其“k级变换点”B分别在直线l1，l2上，在l1，l2上分别取点（m2，y1），（m2，y2）．若k≤﹣2，求证：y1﹣y2≥2；
（3）关于x的二次函数y＝nx2﹣4nx﹣5n（x≥0）的图象上恰有两个点，这两个点的“1级变换点”都在直线y＝﹣x+5上，求n的取值范围．








2023年江苏省南通市中考数学试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题3分，共30分。在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）
1．【答案】D
【解答】解：（﹣3）×2＝﹣（3×2）＝﹣6，
故选：D．
2．【答案】B
【解答】解：将41800000000用科学记数法表示为4.18×1010．
故选：B．
3．【答案】A
【解答】解：A．三棱柱的俯视图是三角形，故此选项符合题意；
B．圆柱体的俯视图是圆，故此选项不合题意；
C．四棱锥的俯视图是四边形（画有对角线），故此选项不合题意；
D．圆锥体的俯视图是圆（带圆心），故此选项不合题意．
故选：A．
4．【答案】C
【解答】解：∵3＜＜4，而数轴上A，B，C，D，E五个点分别表示数1，2，3，4，5，
∴表示数 的点应在线段CD上，
故选：C．
5．【答案】A
【解答】解：如图，

∵m∥n，∠1＝50°，
∴∠ACD＝∠1＝50°，
∵∠ACB＝90°，
∴∠BCD＝∠ACB﹣∠ACD＝40°，
∴∠2＝180°﹣∠BCD＝140°．
故选：A．
6．【答案】D
【解答】解：∵a2﹣4a﹣12＝0，
∴a2﹣4a＝12，
∴2a2﹣8a﹣8
＝2（a2﹣4a）﹣8
＝2×12﹣8
＝24﹣8
＝16，
故选：D．
7．【答案】B
【解答】解：过点A作AD⊥BC，垂足为D，

由题意得：AD＝120m，
在Rt△ABD中，∠BAD＝30°，
∴BD＝AD•tan30°＝120×＝40（m），
在Rt△ACD中，∠CAD＝60°，
∴CD＝AD•tan60°＝120（m），
∴BC＝BD+CD＝160（m），
∴这栋楼的高度为160m，
故选：B．
8．【答案】C
【解答】解：∵BE＝BC，DE＝CD，BD＝BD，
∴△CBD≌△EBD（SSS），
∴∠CBD＝∠EBD，
∵四边形ABCD是矩形，
∴AD∥BC，AD＝BC＝8，∠A＝90°，
∴∠ADB＝∠CBD，
∴∠ADB＝∠EBD，
∴OB＝OD，
设AO＝x，则OD＝8﹣x，
∴OB＝8﹣x，
由勾股定理得：AB2+AO2＝OB2，
∴42+x2＝（8﹣x）2，
∴x＝3，
∴tan∠ABE＝＝．
故选：C．

9．【答案】B
【解答】解∵∠C＝90°，AC＝15，BC＝20，
∴AB＝＝＝25，
①当0≤x≤15时，点P在AC边上，如图所示，

此时AD＝x，
∵ED⊥AB，
∴∠DEA＝90°＝∠C，
∵∠CAB＝∠EAD，
∴△CAB∽△EAD，
∴＝＝，
∴AE＝＝，
DE＝＝，
BE＝25﹣，
∴y＝BE•DE＝×（25﹣）×＝10x﹣，
当x＝10时，y＝76，
∴a＝76，
②当15＜x≤35时，点P在BC边上，如图所示，

此时BP＝35﹣x，
∵DE⊥AB，
∴∠DEB＝90°＝∠C，
∵∠DBE＝∠ABC，
∴△DBE∽△ABC，
∴，
∴BE＝＝＝28﹣，
DE＝＝＝21﹣，
∴y＝DE•BE＝×（28﹣）×（21﹣）＝（14﹣）（21﹣），
当x＝25时，y＝24，
∴b＝24，
∴a﹣b＝76﹣24＝52，
故选：B．
10．【答案】D
【解答】解：由题意可得，
解得：，
则﹣2xy+1
＝﹣2××+1
＝﹣+1
＝﹣+1
＝﹣+1
＝﹣+≤，
∵3＞＞2＞，
∴A，B，C不符合题意，D符合题意，
故选：D．
二、填空题（本大题共8小题，第11～12题每小题3分，第13～18题每小题3分，共30分，不需写出解答过程，请把答案直接填写在答题卡相应位置上）
11．【答案】2．
【解答】解：原式＝2．
故答案为：2．
12．【答案】见试题解答内容
【解答】解：a2﹣ab＝a（a﹣b）．
13．【答案】．
【解答】解：∵D，E分别是AB，AC的中点，
∴，
又∵∠A＝∠A，
∴△ADE∽△ABC，
∴＝（）2＝．
故答案为：．
14．【答案】2500．
【解答】解：设功率为P，由题可知P＝FV，即v＝，将F＝3750N，v＝20m/s代入可得：P＝75000，即反比例函数为：v＝．当v＝30m/s时，F＝＝2500N．
胡答案为：2500．
15．【答案】24．
【解答】解：如图，连接OD，

∵OA＝OD，∠DAB＝66°，
∴∠ODA＝∠OAD＝66°，
∴∠AOD＝180°﹣66°﹣66°＝48°，
∴∠ACD＝∠AOD＝24°，
故答案为：24．
16．【答案】m．
【解答】解：∵a，b，c是勾股数，其中a，b均小于c，a＝m2﹣，，
∴b2＝c2﹣a2
＝（m2+）2﹣（m2﹣）2
＝m4++m2﹣（m4+﹣m2）
＝m4++m2﹣m4﹣+m2
＝m2，
∵m是大于1的奇数，
∴b＝m．
故答案为：m．
17．【答案】k≥1．
【解答】解：∵一次函数y＝x﹣k，
∴y随x的增大而增大，
∵对于x＜3范围内任意自变量x的值，其对应的函数值y都小于2k，
∴3﹣k≤2k，
解得k≥1，
故答案为：k≥1．
18．【答案】．
【解答】解：设AC，BD的交点为O，AB，BC，CD，DA的中点分别是P，Q，R，S，连接PQ，QR，RS，SP，OQ，OS，QS，如图：

∵AC，BD互相垂直，
∴△AOD和△BOC为直角三角形，且AD，BC分别为斜边，
∴AD＝2OS，BC＝2OQ，
∴AD+BC＝2（OS+OQ），
∴当OS+OQ为最小时，AD+BC为最小，
根据“两点之间线段最短”得：OQ+OS≥QS，
∴当点O在线段QS上时，OQ+OS为最小，最小值为线段QS的长，
∵点P，Q分别为AB，BC的中点，
∴PQ为△ABC的中位线，
∴PQ＝AC＝2，PQ∥AC，
同理：QR＝BD＝3，QR∥BD，RS＝AC＝2，RS∥AC，SP＝BD＝3，SP∥BD，
∴PQ∥AC∥RS，QR∥BD∥SP，
∴四边形PQRS为平行四边形，
∵AC⊥BD，PQ∥AC，SP∥BD，
∴PQ⊥SP，
∴四边形PQRS为矩形，
在Rt△PQS中，PQ＝2，SP＝3，
由勾股定理得：，
∴OQ+OS的最小值为，
∴AD+BC的最小值为．
故答案为：．
三、解答题（本大题共8小题，共90分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．【答案】（1）；
（2）1．
【解答】解：（1），
②﹣①得：x＝2，
把x＝2代入①得：4+y＝3，
解得：y＝﹣1，
故原方程组的解是：；
（2）
＝
＝
＝
＝1．
20．【答案】（1）90；
（2）八年级成绩较好，理由见解析．
【解答】解：（1）若该校八年级共有300名学生参赛，估计优秀等次的约有300×＝90（人），
故答案为：90；
（2）八年级成绩较好，理由如下：
因为七、八年级的平均数相等，而八年级的众数和中位数大于七年级的众数和中位数，
所以八年级得分高的人数较多，即八年级成绩较好（答案不唯一）．
21．【答案】（1）二；
（2）证明见解答过程．
【解答】（1）解：小虎同学的证明过程中，第二步出现错误，
故答案为：二；
（2）证明：∵∠ADC＝∠AEB＝90°，
∴∠BDC＝∠CEB＝90°，
在△DOB和△EOC中，
，
∴△DOB≌△EOC（AAS），
∴OD＝OE，
在Rt△ADO和Rt△AEO中，
，
∴Rt△ADO≌Rt△AEO（HL），
∴∠1＝∠2．
22．【答案】（1）；
（2）．
【解答】解：（1）∵有同型号的a，b，c三把钥匙，
∴从三把钥匙中随机取出一把钥匙，取出c钥匙的概率等于，
故答案为：；
（2）画树状图如下：

共有6种等可能的结果，其中取出的钥匙恰好能打开取出的锁的结果有2种，即Aa、Bb，
∴取出的钥匙恰好能打开取出的锁的概率为＝．
23．【答案】（1）证明过程见解答；
（2）图中阴影部分的面积为﹣2．
【解答】（1）证明：连接OC，

∵⊙O和底边AB相切于点C，
∴OC⊥AB，
∵OA＝OB，∠AOB＝120°，
∴∠AOC＝∠BOC＝∠AOB＝60°，
∵OD＝OC，OC＝OE，
∴△ODC和△OCE都是等边三角形，
∴OD＝OC＝DC，OC＝OE＝CE，
∴OD＝CD＝CE＝OE，
∴四边形ODCE是菱形；
（2）解：连接DE交OC于点F，

∵四边形ODCE是菱形，
∴OF＝OC＝1，DE＝2DF，∠OFD＝90°，
在Rt△ODF中，OD＝2，
∴DF＝＝＝，
∴DE＝2DF＝2，
∴图中阴影部分的面积＝扇形ODE的面积﹣菱形ODCE的面积
＝﹣OC•DE
＝﹣×2×2
＝﹣2，
∴图中阴影部分的面积为﹣2．
24．【答案】（1）x的值为600；
（2）该段时间内体育中心至少需要支付56800元施工费用．
【解答】解：（1）根据题意得：＝，
解得：x＝600，
经检验，x＝600是所列方程的解，且符合题意．
答：x的值为600；
（2）设甲工程队施工m天，则乙工程队单独施工（22﹣m）天，
根据题意得：（600+300）m+600（22﹣m）≥15000，
解得：m≥6，
设该段时间内体育中心需要支付w元施工费用，则w＝3600m+2200（22﹣m），
即w＝1400m+48400，
∵1400＞0，
∴w随m的增大而增大，
∴当m＝6时，w取得最小值，最小值＝1400×6+48400＝56800．
答：该段时间内体育中心至少需要支付56800元施工费用．
25．【答案】（1）AF；
（2）45°或135°；
（3）﹣1．
【解答】解：（1）∵四边形ABCD是正方形，
∴AB＝AD，∠B＝∠D＝90°，
∵BE＝BF，
∴△ABE≌△ADF（SAS），
∴AE＝AF，
故答案为：AF；
（2）当E点在BC边上时，如图1，
过G点作GM⊥AD交于M，延长MG交BC于N点，
∴∠AMG＝∠DMG＝∠GNE＝90°，
∴四边形CDMN是矩形，
∴∠AGM+∠MAG＝90°，
∵EG⊥AF，∠EAF＝45°，
∴∠AGM+∠EGN＝90°，
∵∠AGE＝90°，∠EAF＝45°，
∴△AEG是等腰直角三角形，
∴AG＝EG，
∴∠EGN＝∠MAG，
∴△AMG≌△GNE（AAS），
∴AM＝GN，
∵AM+MD＝GN+MG，
∴MD＝MG，
∴△MDG为等腰直角三角形，
∴∠MDG＝45°，
∴∠GDC＝45°；
当点E在CD边上时，如图2，
过点G作GN⊥DF交于N，延长NG交BA延长线于点M，
∴四边形ADNM是矩形，
同理，△AMG≌△GNE（AAS），
∴GN＝AM＝DN，
∴△NDG为等腰直角三角形，
∴∠GDN＝45°，
∴∠GDC＝180°﹣45°＝135°，
综上所述：∠GDC的度数为45°或135°；
（3）当点F在CD边延长线上时，点E在边CD上，
设GN＝DN＝a，则DG＝a，
∴DF＝DG＝a，
∴FN＝DF﹣DN＝（﹣1）a，
∵GN∥AD，
∴＝＝﹣1．


26．【答案】（1）存在，k＝±；
（2）证明见解答；
（3）0＜n≤1且n≠1/6．
【解答】（1）解：存在，理由：
由题意得，（1，2）的“k级变换点”为：（k，﹣2k），
将（k，﹣2k）代入反比例函数表达式得：﹣4＝k（﹣2k），
解得：k＝±；

（2）证明：由题意得，点B的坐标为：（kt，﹣kt+2k），
由点A的坐标知，点A在直线y＝x﹣2上，同理可得，点B在直线y＝﹣x+2k，
则y1＝m2﹣2，y2＝﹣m2+2k，
则y1﹣y2＝m2﹣2+﹣m2﹣2k＝m2﹣2k﹣2，
∵k≤﹣2，则﹣2k﹣2+m2≥2，
即y1﹣y2≥2；

（3）解：设在二次函数上的点为点A、B，
设点A（s，t），则其“1级变换点”坐标为：（s，﹣t），
将（s，﹣t）代入y＝﹣x+5得：﹣t＝﹣s+5，
则t＝s﹣5，
即点A在直线y＝x﹣5上，
同理可得，点B在直线y＝x﹣5上，
即点A、B所在的直线为y＝x﹣5；
由抛物线的表达式知，其和x轴的交点为：（﹣1，0）、（5，0），其对称轴为x＝2，
当n＞0时，
抛物线和直线AB的大致图象如下：

直线和抛物线均过点（5，0），则点A、B必然有一个点为（5，0），设该点为点B，另外一个点为点A，如上图，
联立直线AB和抛物线的表达式得：y＝nx2﹣4nx﹣5n＝x﹣5，
设点A的横坐标为x，则x+5＝，
∵x≥0，
则﹣5≥0，
解得：n≤1，
此外，直线AB和抛物线在x≥0时有两个交点，故Δ＝（﹣4n﹣1）2﹣4n（5﹣5n）＝（6n﹣1）2＞0，
故n≠，
即0＜n≤1且n≠；
当n＜0时，
当x≥0时，直线AB不可能和抛物线在x≥0时有两个交点，
故该情况不存在，
综上，0＜n≤1且n≠1/6．