
2022-2023学年北京市海淀区清华附中上地学校八年级(下)期中数学试卷(含解析)
展开2022-2023学年北京市海淀区清华附中上地学校八年级(下)期中数学试卷
一、选择题(本题共8小题,共24分)
1. 一次函数y=-4x+2的图象与y轴交点的坐标是( )
A. (0,2) B. (2,0) C. (12,0) D. (0,12)
2. 在Rt△ABC中,∠C=90°,斜边AB=8,则斜边上的中线CD=( )
A. 2 B. 4 C. 8 D. 16
3. 下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A. 2,3,4 B. 1, 2, 3 C. 1,1,2 D. 5,12,15
4. 下列运算结果正确的是( )
A. 2 3+3 2=5 5 B. 25=±5
C. 15÷ 5=3 D. 5-2=125
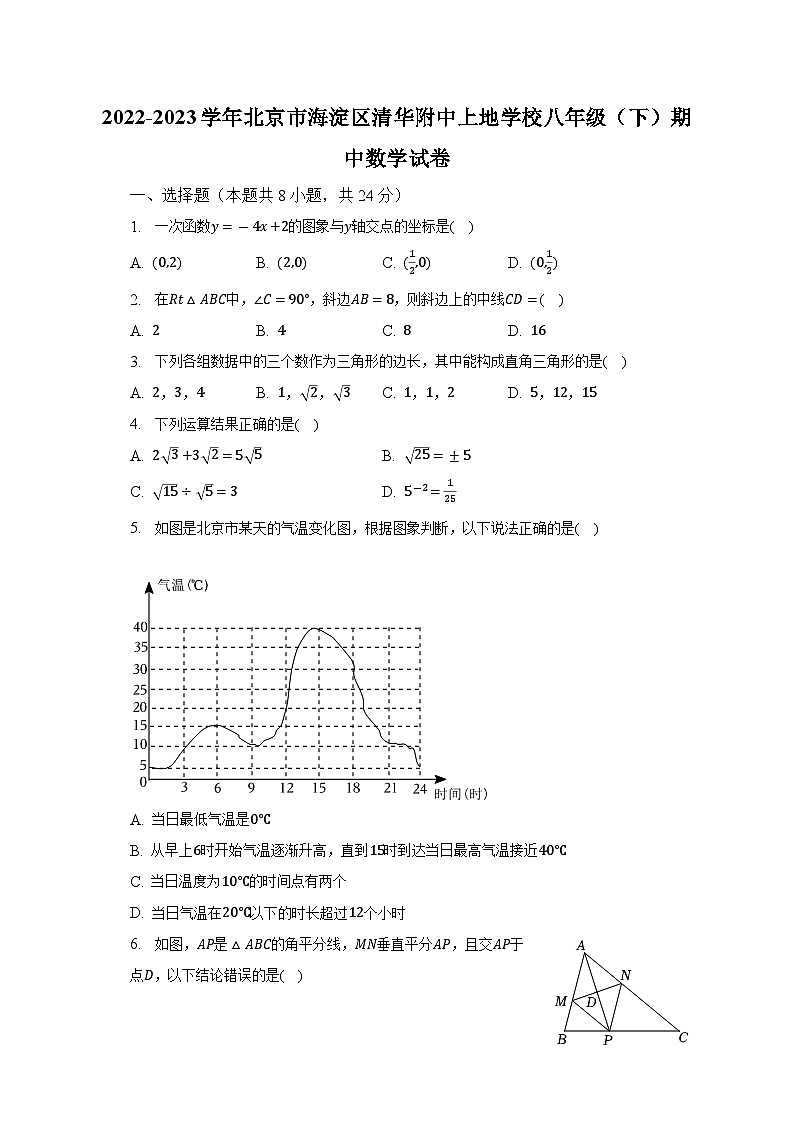
5. 如图是北京市某天的气温变化图,根据图象判断,以下说法正确的是( )
A. 当日最低气温是0℃
B. 从早上6时开始气温逐渐升高,直到15时到达当日最高气温接近40℃
C. 当日温度为10℃的时间点有两个
D. 当日气温在20℃以下的时长超过12个小时
6. 如图,AP是△ABC的角平分线,MN垂直平分AP,且交AP于点D,以下结论错误的是( )
A. PA是∠MPN的平分线
B. PM=PN
C. MP是△ABC的中位线
D. PM=AM
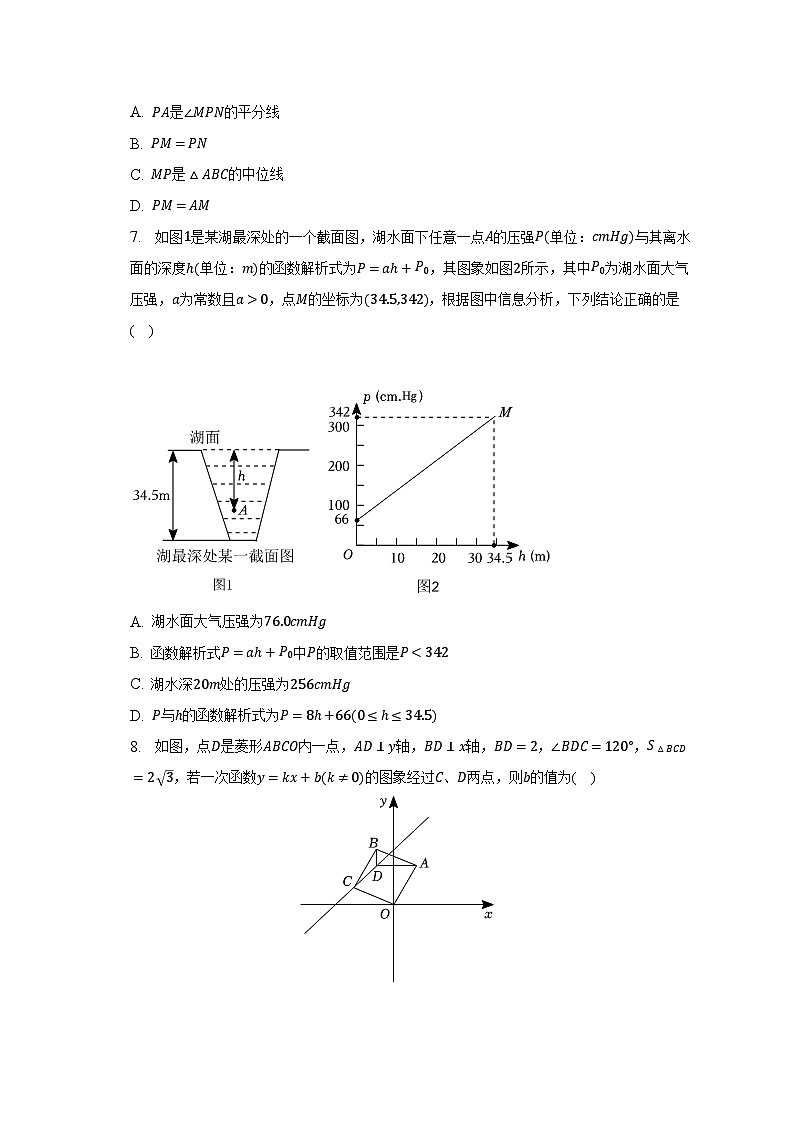
7. 如图1是某湖最深处的一个截面图,湖水面下任意一点A的压强P(单位:cmHg)与其离水面的深度h(单位:m)的函数解析式为P=ah+P0,其图象如图2所示,其中P0为湖水面大气压强,a为常数且a>0,点M的坐标为(34.5,342),根据图中信息分析,下列结论正确的是( )
A. 湖水面大气压强为76.0cmHg
B. 函数解析式P=ah+P0中P的取值范围是P<342
C. 湖水深20m处的压强为256cmHg
D. P与h的函数解析式为P=8h+66(0≤h≤34.5)
8. 如图,点D是菱形ABCO内一点,AD⊥y轴,BD⊥x轴,BD=2,∠BDC=120°,S△BCD=2 3,若一次函数y=kx+b(k≠0)的图象经过C、D两点,则b的值为( )
A. 2+1 B. 2( 2+1) C. 3 D. 33
二、填空题(本题共12小题,共36分)
9. 在△ABC中,D、E分别是AB、AC的中点,DE=4,则BC=______.
10. 如图,在平面直角坐标系xOy中,若A点的坐标为(4,4),B点的坐标为(1,0),则AB的长为______ .
11. 在函数y= x+2+1x-1中,自变量x的取值范围是______ .
12. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F在AC上,且AE=CF,连接BE,ED,DF,FB.若添加一个条件使四边形BEDF是矩形,则该条件可以是 .(填写一个即可)
13. 若A(2 3,y1),B(3 2,y2)是一次函数y=2x-1的图象上的两个点,则y1与y2的大小关系是y1 ______ y2.(填“>”,“=”或“<”)
14. 如图,在平面直角坐标系中,若直线y1=3x+a,直线y2=-bx+5相交于点A(1,2),则关于x的不等式(3+b)x≤5-a的解集是______ .
15. 荡秋千是中国古代北方少数民族创造的一种运动.小亮想利用所学的勾股定理的知识测算公园里一架秋千的绳索AB的长度.如图.他发现秋千静止时,秋千踏板离地面的垂直高度BC=1m,将踏板往前推送,使秋千绳索到达D的位置,测得推送的水平距离为6m,即DE=6m.此时秋千踏板离地面的垂直高度DF=3m.那么,绳索的长度为 m.
16. 计算机可以帮助我们又快又准地画出函数的图象.用“几何画板”软件画出的函数y=x2(x+3)和y=x+3的图象如图所示.根据图象可知方程x2(x+3)=x+3的解的个数为______ ;若m,n分别满足方程x2(x+3)=5和x+3=5,则m,n的大小关系是______ .
17. a,b为有理数,且a+ 3b= 4+2 3,则a+b= ______ .
18. 已知一次函数y=kx+1,当自变量的取值范围是k≤x≤3时,相应的函数值的范围是a≤y≤7,则a= ______ .
19. 如图,已知矩形纸片ABCD,AB=9,BC=6,将B点折到AD的中点E,折痕MN的长度为______ .
20. 如图,△ABC中,D、E、F分别是BC、CA、AB的中点,G、M、N分别是线段AE、AF、BD上的点,且GM//BC,GN//AB,GN与EF交于点K,如果四边形FKGM面积是2,四边形EKND的面积是3,则△GKE的面积是______ .
三、解答题(本题共11小题,共60分)
21. 计算: 12+| 3-2|+3-(π-3.14)0.
22. 如图,四边形ABCD为平行四边形,E,F是直线BD上两点,且AF//CE.求证:BE=DF.
23. 先化简,后求值:(a+ 3)(a- 3)-a(a-6),其中a=12+ 12.
24. 在平面直角坐标系xOy中,函数y=kx+b(k≠0)的图象过点(2,-3),(-4,0).
(1)求该函数的解析式;
(2)当x>-2时,对于x的每一个值,函数y=-x+m的值都小于函数y=kx+b(k≠0)的值,请直接写出实数m的取值范围.
25. 在Rt△BDE中,∠BDE=90°,C是BE的中点,过点D作AD//BE,且AD=BC,连接AE交CD于F.
(1)求证:四边形ABCD是菱形;
(2)若DB=8,菱形ABCD的面积为40,求BE的长.
26. 某商店出售普通练习本和精装练习本,150本普通练习本和100精装练习本销售总额为1450元;200本普通练习本和50精装练习本销售总额为1100元.
(1)求普通练习本和精装练习本的销售单价分别是多少?
(2)该商店计划再次购进500本练习本,普通练习本的数量不低于精装练习本数量的3倍,已知普通练习本的进价为2元/个,精装练习本的进价为7元/个,设购买普通练习本x个,获得的利润为W元;
①求W关于x的函数关系式;
②该商店应如何进货才能使销售总利润最大?并求出最大利润.
27. 有这样一个问题:探究函数y= x+2x的图象与性质.小华根据学习函数的经验,对函数y= x+2x的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)函数y= x+2x的自变量x的取值范围是______;
(2)如表是y与x的几组对应值.m的值为______;
x
-2
-32
-1
-12
13
12
1
2
3
4
…
y
0
- 23
m
- 6
21
10
3
1
53
64
…
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质:______.
(5)结合函数图象估计 x+2x-x-4=0的解的个数为______个.
28. 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)证明平行四边形ECFG是菱形;
(2)如图2所示,∠ABC=90°,AB=3,BC=5,M是EF的中点,连接CM,DM,求DM的长.
(3)如图3所示,若∠ABC=120°,AB=4,BC=8,线段CG与EF交于点O,点M是线段EF上的一个动点,连接CM,DM,直接写出CM+DM的最小值,并写出此时EMOM的值.
29. 在平面直角坐标系xOy中,对于点P和图形W,若图形W上存在点Q,使得直线PQ经过第四象限,则称点P是图形W的“四象点”.已知点A(-2,4),B(2,1).
(1)在点P1(-4,-2),P2(-1,-2),P3(1,-2)中,______ 是线段AB的“四象点”;
(2)已知点C(t,0),D(t+4,0),若等边△CDE(C,D,E顺时针排列)上的点均不是线段AB的“四象点”,求t的取值范围;
(3)已知以E(-92,2),F(-12,2),G(-12,-2),H(-92,-2)为顶点的正方形,若线段AB上的点P是正方形EFGH的“四象点”,请直接写出点P的横坐标xp的取值范围.
30. 已知四边形ABCD中,AB//CD,M为BC中点,且AM⊥DM,AM=4,DM=3.
(1)求AB+CD的值;
(2)求直线AB与直线CD的距离.
31. 正比例函数图象直线l1和一次函数图象直线l2都过点P(2,6),l1,l2与x轴围成的三角形面积为15,而l1,l2与y轴围成的三角形面积为10.
(1)求直线l1与l2的函数表达式;
(2)求l1与l2相交所成的锐角的度数.
答案和解析
1.【答案】A
【解析】解:当x=0时,y=-4x+2=2,
∴一次函数y=-4x+2的图象与y轴交点的坐标是(0,2),
故选:A.
当x=0时,求出y的值,即可确定一次函数y=-4x+2的图象与y轴交点的坐标.
本题考查了一次函数图象上点的坐标特征,熟练掌握一次函数图象上点的坐标特征是解题的关键.
2.【答案】B
【解析】
【分析】
本题考查了直角三角形斜边上的中线等于斜边的一半,熟练掌握直角三角形斜边上的中线等于斜边的一半是解题关键.
根据直角三角形斜边上的中线等于斜边的一半即可得.
【解答】
解:∵如图,在Rt△ABC中,∠ACB=90°,斜边AB=8,
∴斜边上的中线CD=12AB=4,
故选:B.
3.【答案】B
【解析】解:A、∵22+32=13,42=16,
∴22+32≠42,
∴不能构成直角三角形,
故A不符合题意;
B、∵12+( 2)2=3,( 3)2=3,
∴12+( 2)2=( 3)2,
∴能构成直角三角形,
故B符合题意;
C、∵1+1=2,
∴不能构成三角形,
故C不符合题意;
D、∵52+122=169,152=225,
∴52+122≠152,
∴不能构成直角三角形,
故D不符合题意;
故选:B.
根据勾股定理的逆定理进行计算,逐一判断即可解答.
本题考查了勾股定理的逆定理,熟练掌握勾股定理的逆定理是解题的关键.
4.【答案】D
【解析】解:A、2 3与3 2不能合并,故A不符合题意;
B、 25=5,故B不符合题意;
C、 15÷ 5= 3,故C不符合题意;
D、5-2=125,故D符合题意;
故选:D.
根据二次根式的加法,除法法则,二次根式的性质,负整数指数幂进行计算,逐一判断即可解答.
本题考查了二次根式的混合运算,负整数指数幂,准确熟练地进行计算是解题的关键.
5.【答案】D
【解析】解:A.由纵坐标看出,当日最低气温是5℃,故A选项不合题意;
B.由函数图象看出,从早上6时开始气温逐渐升高,直到15时到达当日最高气温接近40℃,故B不合题意;
C.由纵坐标看出,当日温度为10℃的时间点有3个,故C选项不合题意;
D.由函数图象看出,当日气温在20℃以下的时长超过12个小时,故D符合题意;
故选:D.
根据函数图象的纵坐标,可得气温,根据函数图象的增减性,可得答案.
本题考查了函数图象,由纵坐标看出气温,横坐标看出时间是解题关键.
6.【答案】C
【解析】解:∵MN垂直平分AP,
∴AM=PM,AN=PN,
∴∠MAP=∠MPA,∠NAP=∠NPA,
∵AP是△ABC的角平分线,
∴∠MAP=∠NAP,
∴∠MAP=∠MPA=∠NAP=∠NPA,
∴AM//PN,MP//AC,
∴四边形AMPN是平行四边形,
又∵AM=PM,
∴平行四边形AMPN是菱形,
∴AM=AN,PA是∠MPN的平分线,
故选项A、B、D不符合题意,选项C符合题意,
故选:C.
由线段垂直平分线的性质得AM=PM,AN=PN,则∠MAP=∠MPA,∠NAP=∠NPA,再证∠MAP=∠MPA=∠NAP=∠NPA,则AM//PN,MP//AC,得四边形AMPN是平行四边形,然后证平行四边形AMPN是菱形,即可得出结论.
本题考查了菱形的判定与性质、平行四边形的判定与性质、线段垂直平分线的性质、平行线的判定、等腰三角形的性质等知识,熟练掌握菱形的判定与性质是解题的关键.
7.【答案】D
【解析】解:由图象可知,直线P=kh+P0过点(0,66)和(34.5,342).
∴P0=6634.5k+P0=312,
解得k=8P0=66
∴直线解析式为:P=8h+66.故D正确,符合题意;
∴青海湖水面大气压强为66.0cmHg,故A错误,不符合题意;
根据实际意义,函数解析式P=ah+P0中P的取值范围是P<≤342,故B错误,不符合题意;
将h=16.4代入解析式,
∴P=7.1×20+68=210,即青海湖水深20m处的压强为210cmHg,故C错误,不符合题意.
故选:D.
由图象可知,直线P=kh+P0过点(0,66)和(34.5,312).由此可得出k和P0的值,进而可判断B,D;根据实际情况可得出h的取值范围,进而可判断C;将h=16.4代入解析式,可求出P的值,进而可判断A.
本题主要考查一次函数的实际应用,涉及一次函数的图象和性质,待定系数法等知识.关键是计算过程中需要结合实际意义.
8.【答案】B
【解析】解:过点C作CE⊥y轴于点E,延长BD交CE于点F,
∵四边形OABC为菱形,
∴AB//OC,AB=OC,
∴∠COE=∠AGE,
∵BD⊥x轴,AD⊥y轴,
∴BD//y轴,
∴∠ADB=90°,∠AGE=∠ABD,
∴∠COE=∠ABD,
在△COE和△ABD中,
∠CEO=∠ADB=90°∠COE=∠ABDCO=AB,
∴△COE≌△ABD(AAS),
∴OE=BD=2,CE=AD,
∵CE⊥y轴,
∴CE//x轴,
∵BD⊥x轴,
∴BD⊥CE,
又∵CE⊥y轴,AD⊥y轴,
∴四边形DFEH为矩形,
∴FE=DH,
∴CE-FE=AD-DH,
即CF=AH,
∵S△BCD=12⋅BD⋅CF=2 3,
∴CF=2 3,
∴AH=2 3,
∵∠BDC=120°,
∴∠CDF=60°,
∴DF=2.
∴OH=OE+EH=OE+DF=2+2=4,
在Rt△AHO中,由勾股定理得,AO= AH2+OH2= (2 3)2+42=2 7,
∵四边形ABCO是菱形,
∴CO=AO=2 7,
在Rt△AEO中,由勾股定理得,CE= CO2-OE2= (2 7)2-22=2 6,
∴点C的坐标为(-2 6,2),
∴FE=CE-CF=2 6-2 3,
∴点D的坐标为(2 3-2 6,4),
∵一次函数y=kx+b(k≠0)的图象经过C、D两点,
则-2 6k+b=2(2 3-2 6)k+b=4,
解得k= 33b=2( 2+1).
故选:B.
过点C作CE⊥y轴于点E,延长BD交CE于点F,可证明△COE≌△ABD(AAS),则OE=BD=2,由S△BCD=12⋅BD⋅CF=2 3可得CF=2 3,由∠BDC=120°,可知∠CDF=60°,所以DF=2,所以点D的纵坐标为4,再求出AH=CF,利用勾股定理求出AO的长,再利用勾股定理求出CE的长,从而求出C、D的坐标,利用待定系数法求出k,b的值即可.
本题主要考查一次函数函数与几何的综合问题,涉及到菱形的性质,三角形全等的判定与性质,勾股定理等知识点,求出关键点C、D的坐标是解题的关键.
9.【答案】8
【解析】解:如图所示,
∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE,
∵DE=4,
∴BC=2DE=2×4=8.
故答案为:8.
先根据题意画出图形,由D、E分别是AB、AC的中点可知,DE是△ABC的中位线,根据三角形中位线定理解答即可.
此题考查的是三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.
10.【答案】5
【解析】解:∵A点的坐标为(4,4),B点的坐标为(1,0),
∴AB= (4-1)2+(4-0)2=5.
故答案为:5.
根据勾股定理计算即可.
本题考查了点的坐标以及勾股定理,掌握勾股定理是解答本题的关键.
11.【答案】x≥-2且x≠1
【解析】
【分析】
本题考查了函数自变量的取值范围,分式有意义,分母不为0;二次根式的被开方数是非负数.
根据二次根式有意义的条件是:被开方数是非负数,以及分母不等于0,据此即可求解.
【解答】
解:根据题意得:x+2≥0x-1≠0,
解得x≥-2且x≠1.
故答案为x≥-2且x≠1.
12.【答案】OE=12BD
【解析】解:OE=12BD,
理由:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵AE=CF,
∴AO-AE=CO-CE.
即EO=FO.
∴四边形BEDF为平行四边形,
∴OE=OF,OB=OD,
∵OE=12BD,
∴BD=EF,
∴四边形BEDF是矩形.
故答案为:OE=12BD.
根据平行四边形的判定和性质定理以及矩形的判定定理即可得到结论.
此题主要考查了矩形 的判定和性质,平行四边形的判定和性质,熟练掌握平行四边形的判定和性质定理是解题的关键.
13.【答案】<
【解析】解:当x=2 3时,y1=2×2 3-1=4 3-1;
当x=3 2时,y2=2×3 2-1=6 2-1.
∵ 48-1< 72-1,
∴y1
利用一次函数图象上点的坐标特征可求出y1,y2的值,比较后即可得出结论(利用一次函数的性质解决问题亦可).
本题考查了一次函数图象上点的坐标特征,利用一次函数图象上点的坐标特征,求出y1,y2的值是解题的关键.
14.【答案】x≤1
【解析】解:不等式(3+b)x≤5-a变形为3x+a≤-bx+5,
∵直线y1=3x+a,直线y2=-bx+5相交于点A(1,2),
∴当x<1时,函数y1=3x+a的图象都在y2=-bx+5的图象下方,
∴不等式(3+b)x≤5-a的解集为x≤1;
故答案为:x≤1.
不等式(3+b)x≤5-a变形为3x+a≤-bx+5,观察函数图象得到当x<1时,函数y1=3x+a的图象都在y2=-bx+5的图象下方,所以不等式(3+b)x≤5-a的解集为x<1.
本题考查了一次函数与一元一次不等式,正确记忆从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合是解题关键.
15.【答案】10
【解析】解:由题意得:∠AED=90°,
在Rt△AED中,由勾股定理得:AE2+ED2=AD2,
设绳索AD的长度为xm,则AE=(x-2)m,
∴x2=62+(x-2)2,
解得:x=10,
答:绳索AD的长度是10m.
故答案为:10.
设绳索AD的长度为xm,则AE=(x-2)m,在Rt△AED中,由勾股定理得出方程,解方程即可.
本题考查了勾股定理的应用,由勾股定理得出方程是解题的关键.
16.【答案】3 m
所以方程x2(x+3)=x+3的解的个数为3;
作直线y=5,
如图,函数y=x2(x+3)的图象与直线y=5,
y=x+3的图象与直线y=5的交点(2,5),
则m
本题考查了抛物线与x轴的交点:把方程解的问题转化为两函数图象的交点问题.利用数形结合的思想是解决此类问题的关键.
17.【答案】解:原式=2 3+2- 3+3-1
= 3+4.
【解析】直接利用二次根式的性质以及绝对值的性质、零指数幂的性质分别化简,进而得出答案.
此题主要考查了实数的运算,正确化简各数是解题关键.
18.【答案】证明:∵四边形ABCD是平行四边形,
∴AD//BC,AD=BC,
∴∠ADB=∠DBC,
∵∠ADF+∠ADB=180°,∠CBE+∠DBC=180°,
∴∠ADF=∠CBE,
∵AF//CE,
∴∠F=∠E,
在△ADF和△CBE中,
∠F=∠E∠ADF=∠CBEAD=CB,
∴△ADF≌△CBE(AAS),
∴DF=BE.
【解析】证明△ADF≌△CBE(AAS),由全等三角形的性质即可解决问题.
此题考查的是平行四边形的性质、全等三角形的判定与性质,掌握其性质定理是解决此题的关键.
19.【答案】解:∵a=12+ 12=12+12 2,
∴(a+ 3)(a- 3)-a(a-6),
=a2-3-a2+6a,
=6a-3,
=6×(12+12 2)-3,
=3 2.
【解析】求出a的值,根据平方差公式得出a2-3-a2+6a,推出6a-3,把a的值代入求出即可.
本题考查了平方差公式和二次根式的化简求值的应用,关键是根据性质进行化简,题目比较好,但是一道比较容易出错的题目.
20.【答案】解:(1)把(2,-3),(-4,0)代入y=kx+b得:
2k+b=-3-4k+b=0,
解得k=-12b=-2,
∴函数的解析式为y=-12x-2;
(2)根据题意,由(1)可得:-x+m<-12x-2,
解得x>2m+4,
∵当x>-2,对于x的每一个值,函数y=-x+m的值都小于函数y=-12x-2的值,
∴2m+4≤-2,
解得:m≤-3.
【解析】(1)通过待定系数法将点(2,-3),(-4,0)代入解析式求出k,b的值,进而可得函数的解析式;
(2)根据题意得出-x+m<-12x-4,求出x得取值范围,结合x>-2即可得出m的取值范围.
本题考查了待定系数法求一次函数的解析式,熟练掌握待定系数法求函数解析式及函数的性质是解题的关键.
21.【答案】(1)证明:AD//BE,且AD=BC,
∴四边形ABCD是平行四边形,
∵点C是BE边的中点,∠BDE=90°,
∴BC=CE=DC,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴AB=AD=CD=BC,
在△ABD和△CDB中,
AB=CDAD=CBBD=DB,
∴△ABD≌△CDB(SSS),
∴S△ABD=SCDB,
∵BC=CE,
∴S△BCD=S△CDE=12S菱形ABCD=12S△BDE,
∴12×8⋅DE=40,
∴DE=10,
∴BE= BD2+DE2= 82+102=2 41.
【解析】(1)由直角三角形斜边中线的性质得到BC=CE=DC,通过证明四边形ABCD是平行四边形,可得结论;
(2)由BC=CE得到S△BCD=S△CDE=12S菱形ABCD=12S△BDE,由三角形的面积公式可求解.
本题考查了菱形的判定和性质,掌握菱形的判定和性质、全等三角形的性质和判定直角三角形斜边中线的性质是解题的关键.
22.【答案】解:(1)设普通练习本的销售单价为m元,精装练习本的销售单价为n元,
由题意可得:150m+100n=1450200m+50n=1100,
解得m=3n=10,
答:普通练习本的销售单价为3元,精装练习本的销售单价为10元;
(2)①购买普通练习本x个,则购买精装练习本(500-x)个,
由题意可得:W=(3-2)x+(10-7)(500-x)=-2x+1500,
∵普通练习本的数量不低于精装练习本数量的3倍,
∴x≥3(500-x),
解得x≥375,
即W关于x的函数关系式是;W=-2x+1500(375≤x≤500);
②∵W=-2x+1500,
∴W随x的增大而减小,
∵375≤x≤500,
∴当x=375时,W取得最大值,此时W=750,500-x=125,
答:当购买375个普通练习本,125个精装练习,销售总利润最大,最大总利润为750元.
【解析】(1)设普通练习本的销售单价为m元,精装练习本的销售单价为n元,根据等量关系式:150本普通练习本销售总额+100精装练习本销售额=1450元;200本普通练习本销售额+50精装练习本销售额=1100元,列出方程组,求出即可;
(2)①购买普通练习本x个,则购买精装练习本(500-x)个,根据总利润=普通练习本获得的利润+精装练习本获得的利润,列出关系式,然后再求出自变量x的取值范围即可;
②根据一次函数的性质和x的取值范围,可以得到商店应如何进货才能使销售总利润最大,并求出最大利润.
本题主要考查二元一次方程组、一次函数的应用、一元一次不等式组的应用,解题的关键是找出题目中的等量关系和不等关系列出方程和不等式.
23.【答案】x≥-2且x≠0 -1 在每个象限内,函数y随x增大而减小,(答案不唯一) 1
【解析】解:(1)由题意得:x+2≥0且x≠0,解得x≥-2且x≠0,
故答案为x≥-2且x≠0;
(2)当x=-1时,y= x+2x= 2-1-1=-1=m,
故答案为-1;
(3)描点连线绘出如下函数图象:
(4)从图象看,在每个象限内,函数y随x增大而减小,
故答案为在每个象限内,函数y随x增大而减小(答案不唯一);
(5)在(3)的基础上,画出y=x+4的图象,
从图象看,两个函数有1个交点,
故答案为1.
(1)由题意得:x+2≥0且x≠0,即可求解;
(2)当x=-1时,y= x+2x= 2-1-1=-1=m;
(3)描点连线绘出函数图象即可;
(4)从图象看,函数y随x增大而减小,进而求解;
(5)在(3)的基础上,画出y=x+4的图象,从图象看,两个函数有1个交点,即可求解.
本题考查了反比例函数的性质,函数图象的画法,画出函数图象是解本题的关键.
24.【答案】(1)证明:∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形.
∴AD//BC,AB//CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形.
(2)解:如图,连接BD、BM,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
∴∠BCD=90°,AB=CD,
∴∠ECF=180°-∠BCD=90°,
又由(1)可知四边形ECFG为菱形,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,四边形ECFG为正方形.
∴∠CEM=∠ECM=45°,∠CEG=90°,∠BEG=180°-∠CEG=90°,
∴∠BEM=∠DCM=135°,CM=EM,∠CME=180°-45°-45°=90°,
∴△BME≌△DMC(SAS),
∴MB=MD,∠DMC=∠BME,
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=3,BC=5,
∴BD2=32+52=34,
∵BD2=BM2+DM2,
∴DM= 17.
(3)解:如图,连接GM,DG,
∵四边形ABCD是平行四边形,
∴AB//DC,AB=DC=4,AD//BC,
∴∠BAE=∠DAE=∠BEA,
∴BE=AE=4,
∴CE=BC-BE=8-4=4,
∵∠ABC=120°,AB//DC,AD//BC,
∴∠BCD=60°,∠BCF=120°,
由(1)知四边形CEGF是菱形,
∴CE=GE,EG//DF,CE=GE=GF=CF,∠CFG=∠CEG,∠GCF=12∠BCF=60°,CM=GM.
∴∠CEG=∠BCD=60°,
∴△CEG是等边三角形,
∴CG=GE=CE=GF=CD=4,∠CFG=∠CEG=60°,
∴∠FDG=∠DGC=12×60°=30°,
∴∠DGF=180°-∠CFG-∠FDG=90°,
∴DG⊥GF,
∴当D、H、M三点共线时,CM+DM最小,最小值为DG的长,
∵DF=CD+CF=8,GF=4,
∴CM+DM的最小值DG= 82-42=4 3,如图,
当CM+DM取最小值时,
∵四边形CEGF是菱形,
∴OA=OC,BC//GF,
∴∠DNC=∠DGF=90°,
∴DG⊥CE,
∵EG=CG,
∴EN=CN,
∴点M是△EGC的重心,
∴EM=2OM,
∴EMOM=2.
【解析】(1)根据平行四边形的性质可得AD//BC,AB//CD,再根据平行线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再由条件四边形ECFG是平行四边形,可得四边形ECFG为菱形,即可解决问题;
(2)首先证明四边形ECFG为正方形,再证明△BME≌△DMC,可得DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到△BDM是等腰直角三角形,由等腰直角三角形的性质即可得到结论.
(3)如图3,连接GH,DG,先证明△CEG是等边三角形,从而得CG=GE=CE=GF=CD=4∠CFG=∠CEG=60°,进而证DG⊥GF,得当D、H、M三点共线时,CM+DM最小,最小值为DG的长,利用勾股定理求得最小值,再证明点M是△EGC的重心,即可求得EMOM=2.
本题考查相似型综合应用,主要考查平行四边形的判定方法,全等三角形的判定与性质,等边三角形的判定与性质,菱形的判定与性质,三角形的重心等知识点,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法是解题的关键.
25.【答案】P2,P3
【解析】解:(1)如图:
设直线P1B的解析式为y1=kx+b,
将P(-4,-2),B(2,1)代入得-4k+b=-22k+b=1,
解得:k=12b=0,
∴直线P1B的解析式为y1=12x,
故直线P1B经过原点,
∴由函数图象可知,线段AB上不存在一点使得其与P1所在的直线经过第四象限;
∵P2(-1,-2),B(2,1),
∴直线P2B的解析式为y2=x-1,
∵直线y=x-1经过第四象限,
∴P2是线段AB的四象点;
∵P3(1,-2)在第四象限,
∴P3是线段AB的四象点;
故答案为:P2,P3;
(2)如图:
∵C(t,0),D(t+4,0),△CDE是等边三角形(C,D,E顺时针排列),
∴点E一定在x轴下方,
又∵等边△CDE(C,D,E顺时针排列)上的点均不是线段AB的四象点,
∴点E在第三象限,
如图所示,过点E作EF⊥CD于F
∵C(t,0),D(t+4,0),
∴CD=4,则F(t+2,0)
∴CF=DF=2,
∵△CDE是等边三角形,
∴DE=CD=4,
∴EF= DE2-DF2=2 3,
∴点E的纵坐标为-2 3,
由(1)得直线OB的解析式为y=12x,
当y=-2 3时,x=2y=-4 3,
当直线OB恰好经过点E时,点E的坐标为(-4 3,-2 3),
∴此时t=-4 3-2,
结合函数图象可知,当点E继续向左移动的时候,等边△CDE(C,D,E顺时针排列)上的点均不是线段AB的四象点,向右移动的时候,等边△CDE(C,D,E顺时针排列)上存在一点是线段AB的四象点,
∴当等边△CDE(C,D,E顺时针排列)上的点均不是线段AB的四象点时,t≤-4 3-2;
(3)如图:
∵A(-2,4),B(2,1),
∴直线AB的解析式为Y=-34x+52,
∵G(-12,-2),
∴直线OG的解析式为y=4x,
令-34x+52=4x,
解得:x=1019,
∴P(1019,4019),
结合函数图象可知,当点P右移动的时候,直线PG经过第四象限,即点P是正方形EFGH的“四象点”,
∴若线段AB上的点P是正方形EFGH的“四象点”,则点P的横坐标xP的取值范围为1019
(2)根据题意可知点E一定在x轴下方,进而得到点E一定要在第三象限,如图所示,过点E作EF⊥CD于F,先求出CD=4,F(t+2,0),则CF=DF=2,利用勾股定理求出EF=2 3,则点E的纵坐标为-2 3,当直线OB恰好经过点E时,点E的坐标为(-4 3,-2 3),此时t=-4 3-2,结合函数图象可知,当点E继续向左移动的时候,等边△CDE(C,D,E顺时针排列)上的点均不是线段AB的四象点,向右移动的时候,等边△CDE(C,D,E顺时针排列)上存在一点是线段AB的四象点,故当等边△CDE(C,D,E顺时针排列)上的点均不是线段AB的四象点时,t≤-4 3-2;
(3)待定系数法求得直线AB的解析式为y=-34x+52,直线OG的解析式为y=4x,求得直线OG与直线AB交点的坐标为P(1019,4019),结合函数图象可知,当点P右移动的时候,直线PG经过第四象限,即点P是正方形EFGH的“四象点”,即可求得点P的横坐标xP的取值范围为1019
26.【答案】2
【解析】解:4+2 3=12+2 3+( 3)2=(1+ 3)2,
∵a,b为有理数,且a+ 3b= 4+2 3,
∴a+ 3b=1+ 3,
∴a=1,b=1,
∴a+b=1+1=2.
故答案为:2.
先根据完全平方公式进行变形,再根据二次根式的性质进行计算,求出a、b的值,最后求出a+b即可.
本题考查了二次根式的性质与化简,能正确根据二次根式的性质进行计算是解此题的关键.
27.【答案】5或1-3 6
【解析】解:①当k>0时,y随x的增大而增大,
∴x=3时,y=kx+1=7,
∴3k+1=7,解得k=2,
∴一次函数为y=2x+1,
x=2时,y=2×2+1=5;
②当k<0时,y随x的增大而减小,
∴x=3时,y=3k+1=a,
x=k时,y=k2+1=7,
∴k=- 6或 6(舍去),
a=1-3 6,
综上,a=5或1-3 6.
故答案为:5或1-3 6.
分两种情况:①当k>0时,②当k<0时,根据一次函数的性质求解即可.
本题考查了一次函数的性质,一次函数图象上点的坐标特征,解题关键是分类讨论.
28.【答案】2 10
【解析】解:矩形ABCD中,AB=DC=9,BC=AD=6,∠A=∠B=∠C=∠D=90°,
∵E是AD的中点,
∴AE=DE=12AD=3,
设折叠后点C对应的点为F,由折叠可知:EM=BM,FN=CN,∠F=∠C=90°,EF=BC=6,
在Rt△AME中,AM=AB-BM=9-BM,
由勾股定理得:AE2+AM2=EM2,
∴32+(9-BM)2=BM2,
解得:BM=5,
连接EN,作NH⊥AB于点H,如图:
则∠NHA=∠NHB=90°=∠B=∠C,
∴四边形BCNH是矩形,
∴NH=BC=6,BH=CN,
在Rt△EFN中,EN2=EF2+FN2=62+CN2,
在Rt△EDN中,EN2=DE2+DN2=32+(9-CN)2
∴62+CN2=32+(9-CN)2,
解得:CN=3,
∴BH=CN=3,
在Rt△MNH中,
MH=BM-BH=5-3=2,由勾股定理,得:MN= MH2+NH2= 22+62=2 10,
即折痕MN的长度为2 10.
故答案为:2 10.
在Rt△AME中,AM=AB-BM=9-BM,由勾股定理可以求出:BM=5,连接EN,作NH⊥AB于点H,则四边形BCNH是矩形,从而得出:NH=BC=6、BH=CN,设折叠后点C对应的点为F,在Rt△EFN中,由勾股定理得到:EN2=62+CN2,在Rt△EDN中,由勾股定理得到:EN2=DE2+DN2=32+(9-CN)2,从而求出:CN=3,在Rt△MNH中,由勾股定理可以求出折痕MN的长度.
本题主要考查了翻折变换(折叠问题),矩形的性质,勾股定理,解答本题的关键是掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
29.【答案】12
【解析】解:过A作AQ//BC,延长DE交AQ于Q,延长NG交AQ于P,延长MG交QE于L,
∵D,E,F分别是BC,AC,AB的中点,
∴DE,EF是△ABC的中位线,
∴EQ//FA,EF//BC,
∴EF//AQ,
∴四边形AFEQ是平行四边形,
∵ML//BC,NG//AB,
∴四边形AMGP,四边形GKEL是平行四边形,
∴△AFE的面积=△AQE的面积,△AMG的面积=△APG的面积,△KGE的面积=△LGE的面积,
∴平行四边形MFKG的面积=平行四边形QPGL的面积=2,
∵NK=BF,PK=AF,
∵AF=BF,
∴NK=PK,
∴平行四边形PKEQ的面积=平行四边形NDEK的面积=3,
∴平行四边形GKEL的面积=3-2=1,
∴△GKE的面积=12.
故答案为:12.
过A作AQ//BC,延长DE交AQ于Q,延长NG交AQ于P,延长MG交QE于L,由平行四边形的性质推出平行四边形MFKG的面积=平行四边形QPGL的面积=2,平行四边形PKEQ的面积=平行四边形NDEK的面积=3,得到平行四边形的GKEL的面积=1,即可求出△GKE的面积.
本题考查三角形中位线定理,平行四边形的性质,三角形的面积,平行四边形的面积,关键是由平行四边形的性质证明:平行四边形PKEQ的面积=平行四边形NDEK的面积.
30.【答案】解:(1)延长DM交AB的延长线于点E,如图,
∵AB//CD,
∴∠CDM=∠BEM,∠C=∠EBM,
∵M为BC中点,
∴CM=BM,
在△CDM与△BEM中,
∠C=∠EBM∠CDM=∠BEMCM=BM,
∴△CDM≌△BEM(AAS),
∴EM=DM=3,CD=BE,
∵AM⊥DM,
∴∠AME=90°,
∴AE= AM2+EM2= 42+32=5,
∴AB+BE=5,
∴AB+CD=5;
(2)过点M作MF⊥BE,如图,
在Rt△AME中,12AE⋅MF=12AM⋅ME,
则12×5MF=12×4×3,
解得:MF=125,
∵点M是中点,
∴直线AB与直线CD的距离为:2MF=245.
【解析】(1)延长DM交AB的延长线于点E,由平行线的性质可得∠CDM=∠BEM,∠C=∠EBM,再由中点可得CM=BM,可判定△CDM≌△BEM,则有EM=DM=3,CD=BE,再由垂直可得∠AME=90°,利用勾股定理即可求AE,从而可求解;
(2)利用三角形的面积可求得点M到AB的距离,结合M是中点,即可求AB与CD的距离.
本题主要考查全等三角形的判定与性质,平行线之间的距离,解答的关键是作出适当的辅助线.
31.【答案】解:(1)如图,设正比例函数解析式为y=kx,
∵正比例函数图象直线l1过点P(2,6),
∴6=2k,即k=3,
∴直线l1的函数表达式为y=3x;
设直线l2的函数表达式为y=mx+n,
∵l1,l2与x轴围成的三角形面积为15,
∴12×AO×6=15,
解得AO=5,
即直线l2与x轴交于A(5,0)或C(-5,0),
把P(2,6),A(5,0)代入y=mx+n,可得
6=2m+n0=5m+n,解得m=-2n=10,
∴y=-2x+10,
∴B(0,10),
此时S△BOP=12BO×2=12×10×2=10(符合题意);
把P(2,6),C(-5,0)代入y=mx+n,可得
6=2m+n0=-5m+n,解得m=67n=307,
∴y=67x+307,
∴C(0,307),
此时S△DOP=12DO×2=12×307×2=307≠10(不符合题意);
∴直线l2的函数表达式y=-2x+10;
(2)如图,过O作OH⊥AB于H,
由题可得,OP= 22+62=2 10,AP= 32+62=3 5,
设PH=x,则AH=3 5-x,
根据勾股定理,可得(2 10)2-x2=52-(3 5-x)2,
解得x=2 5,
∴Rt△POH中,cos∠OPH=PHPO=2 52 10= 22,
∴∠OPH=45°,
即l1与l2相交所成的锐角的度数为45°.
【解析】(1)依据正比例函数图象直线l1过点P(2,6),即可得到直线l1的函数表达式为y=3x;依据l1,l2与x轴围成的三角形面积为15,直线l2与x轴交于A(5,0),根据待定系数法即可得到直线l2的函数表达式y=-2x+10;
(2)过O作OH⊥AB于H,设PH=x,则AH=3 5-x,根据勾股定理,可得(2 10)2-x2=52-(3 5-x)2,求得x的值即可得到cos∠OPH=PHPO=2 52 10= 22,进而得出∠OPH=45°.
本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.
2022-2023学年北京市海淀区清华附中上地学校九年级(下)开学数学试卷(含解析): 这是一份2022-2023学年北京市海淀区清华附中上地学校九年级(下)开学数学试卷(含解析),共26页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2021-2022学年北京市海淀区清华附中上地学校八年级(下)期中数学试卷: 这是一份2021-2022学年北京市海淀区清华附中上地学校八年级(下)期中数学试卷,共36页。
2022-2023学年北京市海淀区清华附中八年级(下)期中数学试卷(含解析): 这是一份2022-2023学年北京市海淀区清华附中八年级(下)期中数学试卷(含解析),共28页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












