初中数学苏科版八年级上册1.2 全等三角形精练

这是一份初中数学苏科版八年级上册1.2 全等三角形精练，文件包含专题14全等三角形综合和常见全等模型汇总-《讲亮点》2022-2023学年八年级数学上册教材同步配套讲练苏科版原卷版docx、专题14全等三角形综合和常见全等模型汇总-《讲亮点》2022-2023学年八年级数学上册教材同步配套讲练苏科版解析版docx等2份试卷配套教学资源，其中试卷共109页， 欢迎下载使用。
1、掌握全等三角形证明中的几种常见全等模型；
2、掌握全等三角形的综合运用；
【教学重难点】
1、全等三角形中的平移模型；
2、全等三角形中的轴对称模型；
3、全等三角形中的倍长中线模型；
4、全等三角形中的角平分线模型；
5、全等三角形中的手拉手模型
6、全等三角形中的动态问题。
【知识亮解】
知识点一、全等三角形的判定与性质
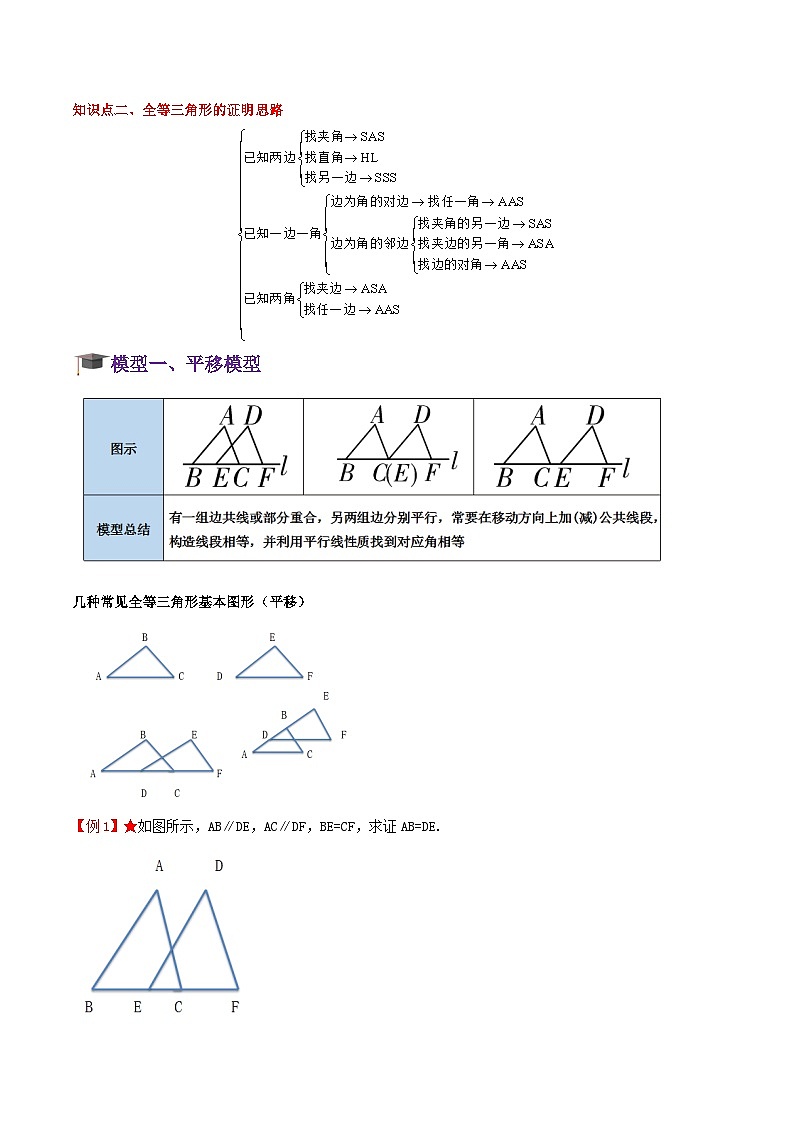
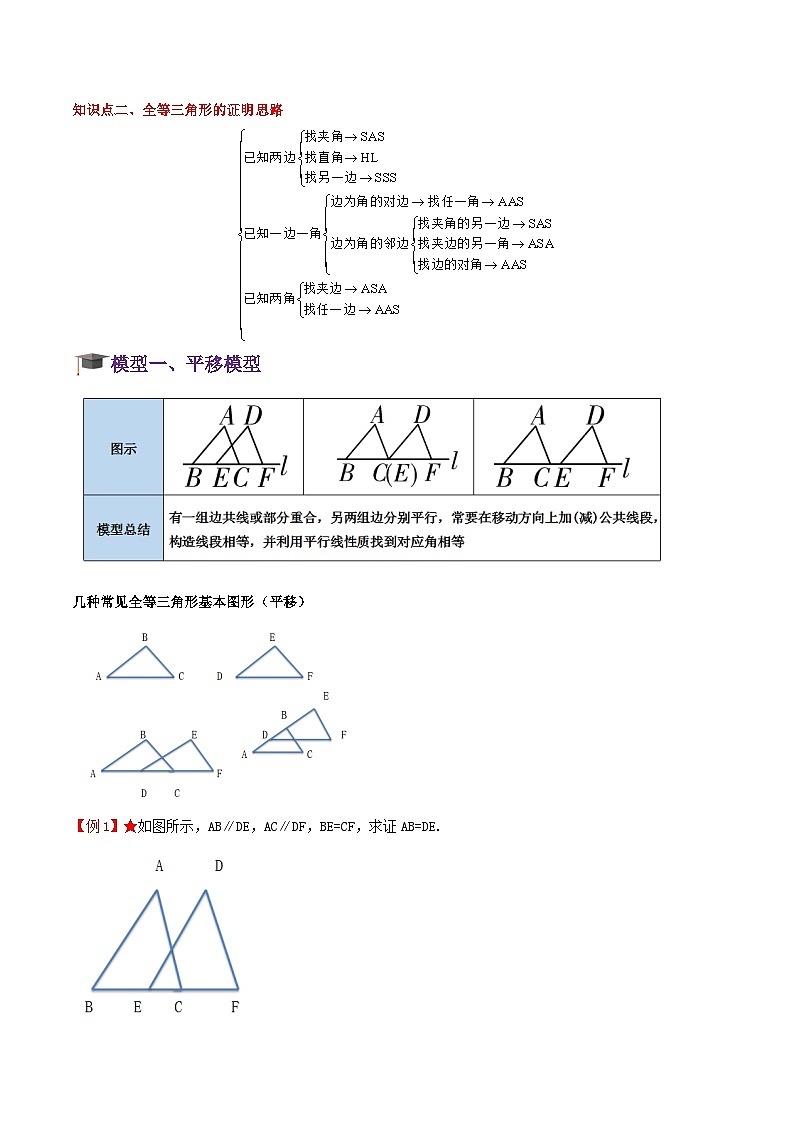
知识点二、全等三角形的证明思路
模型一、平移模型
几种常见全等三角形基本图形（平移）
【例1】★如图所示，AB∥DE，AC∥DF，BE=CF，求证AB=DE.
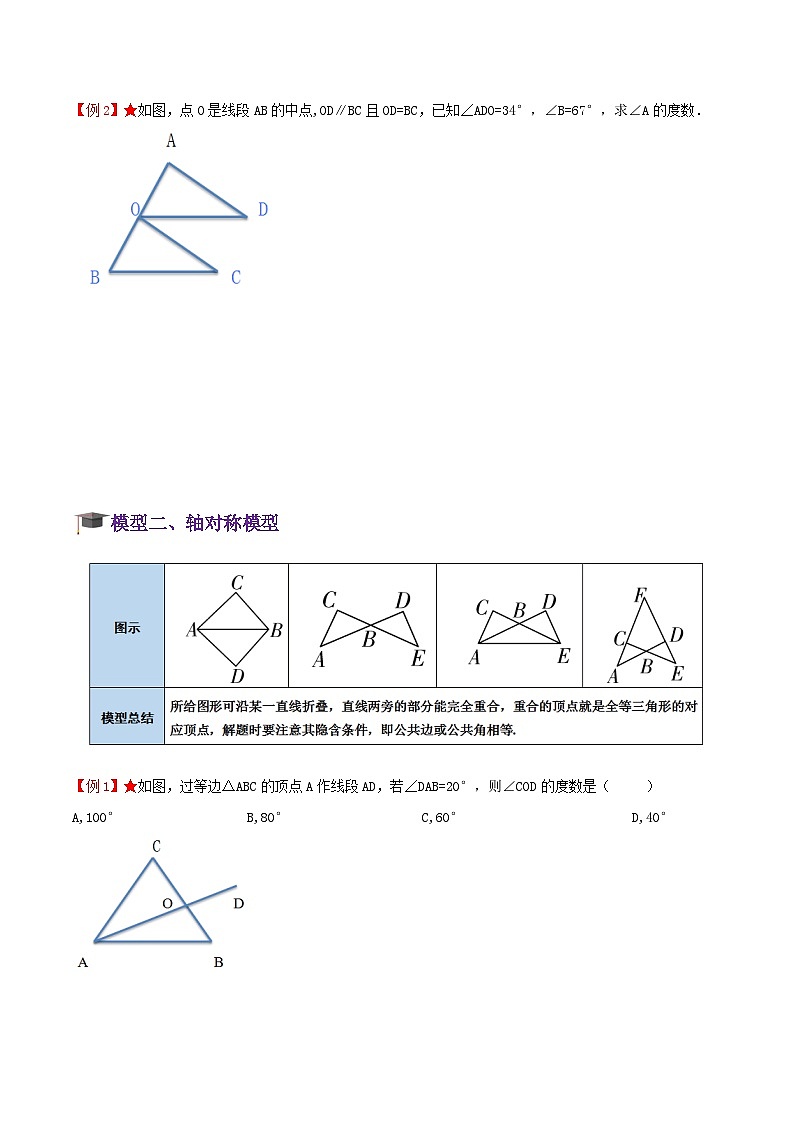
【例2】★如图，点O是线段AB的中点,OD∥BC且OD=BC，已知∠ADO=34°，∠B=67°，求∠A的度数．
模型二、轴对称模型
【例1】★如图，过等边△ABC的顶点A作线段AD，若∠DAB=20°，则∠COD的度数是（ ）
A,100° B,80° C,60° D,40°
【例2】★★在等边△ABC,点E是AB上的动点，点E与点A，B不重合，点D在CB的延长线上，且EC=ED。
如图1，当BE=AE时，求证BD=AE
当BE≠AE，BD=AE能否成立？请说明理由。
模型三、倍长中线模型
一．中点类辅助线作法
见到中线(中点)，我们可以联想的内容无非是倍长中线或者是与中点有关的一条线段，尤其是在涉及线段的等量关系时，倍长中线的应用更是较为常见，常见添加方法如下图（ 是底边的中线)．
二．截长补短类辅助线作法
截长补短法，是初中数学几何题中一种辅助线的添加方法，也是把几何题化难为易的一种思想．所谓“截长”，就是将三者中最长的那条线段一分为二，使其中的一条线段等于已知的两条较短线段中的一条，然后证明其中的另一段与已知的另一条线段相等；所谓“补短”，就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等，然后求出延长后的线段与最长的已知线段的关系．有的是采取截长补短后，使之构成某种特定的三角形进行求解。
【例1】★阅读下面的题目及分析过程，并按要求进行证明．
已知：如图，E是BC的中点，点A在DE上，且∠BAE=∠CDE．
求证：AB=CD．
分析：证明两条线段相等，常用的一般方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要证明的两条线段，它们不在同一个三角形中，且它们分别所在的两个三角形也不全等．因此，要证AB=CD，必须添加适当的辅助线，构造全等三角形或等腰三角形．
现给出如下三种添加辅助线的方法，请任意选择其中一种，对原题进行证明．
【例2】★★★八年级一班数学兴趣小组在一次活动中进行了探究试验活动，请你和他们一起活动吧．
【探究与发现】
（1）如图1，AD是△ABC的中线，延长AD至点E，使ED=AD，连接BE，写出图中全等的两个三角形______
【理解与应用】
（2）填空：如图2，EP是△DEF的中线，若EF=5，DE=3，设EP=x，则x的取值范围是______．
（3）已知：如图3，AD是△ABC的中线，∠BAC=∠ACB，点Q在BC的延长线上，QC=BC，求证：AQ=2AD．
练习：
1．（2021·甘肃兰州·模拟预测）如图，在△ABC中，AB＝4，AC＝2，点D为BC的中点，则AD的长可能是（ ）
A．1B．2C．3D．4
2．（2021·辽宁·鞍山市第五十一中学八年级阶段练习）如图，已知AD是△ABC中BC边上的中线，AB＝5，AC＝3，则AD的取值范围是（ ）
A．2＜AD＜8B．1＜AD＜4C．2＜AD＜5D．4≤AD≤8
3．（2022·上海·七年级专题练习）如图，已知AD是△ABC的中线，E是AC上的一点，BE交AD于F，AC＝BF，∠DAC＝24°，∠EBC＝32°，则∠ACB＝_____．
4．（2022·全国·八年级）在△ABC中，AB＝AC，点D是△ABC内一点，点E是CD的中点，连接AE，作EF⊥AE，若点F在BD的垂直平分线上，∠BAC＝α，则∠BFD＝_________．（用α含的式子表示）
5．（2021·河北邢台·八年级期中）某数学兴趣小组在一次活动中进行了探究试验活动，请你来加入．
【探究与发现】
如图1，延长△ABC的边BC到D，使DC＝BC，过D作DE∥AB交AC延长线于点E，求证：△ABC≌△EDC．
【理解与应用】
如图2，已知在△ABC中，点E在边BC上且∠CAE＝∠B，点E是CD的中点，若AD平分∠BAE．
（1）求证：AC＝BD；
（2）若BD＝3，AD＝5，AE＝x，求x的取值范围．
模型四、角平分线模型
1 角平分线常用的辅助线
【例1】（2022·全国·八年级）已知：如图，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA，过E作EF⊥AB，F为垂足，下列结论：①△ABD≌△EBC②∠BCE+∠BCD=180°③AD=AE=EC ④ BA+BC=2BF其中正确的是（ ）
A．①②③B．①③④C．①②④D．①②③④
【例2】（浙江杭州·八年级期末）如图，中，，的角平分线、相交于点，过作交的延长线于点，交于点，则下列结论：①；②；③；④四边形，其中正确的个数是（ ）
A．4B．3C．2D．1
【例3】（2022·全国·八年级）如图所示，的外角的平分线CP与的平分线相交于点P，若，则_______．
【例4】（2021·山东淄博·七年级期末）已知，△ABC中，∠BAC＝120°，AD平分∠BAC，∠BDC＝60°，AB＝2，AC＝3，则AD的长是________．
【例5】（2022·全国·八年级）已知：如图，AC∥BD，AE、BE分别平分∠CAB和∠ABD，点E在CD上．用等式表示线段AB、AC、BD三者之间的数量关系，并证明．
模型五、全等三角形中的手拉手模型
手拉手模型是指两个顶角相等的等腰三角形顶角顶点重合，左底角顶点互连，右底角顶点互连所组成的图形。如果把等腰三角形顶角看作“头”，左底角看作“左手”，右底角看作“右手”，则可以描述成：头对头，左手拉左手，右手拉右手，这也正是手拉手模型名称的由来。
【例1】（2022·山东·宁津县育新中学九年级阶段练习）如图，，，三点在同一直线上，，都是等边三角形，连接，，：下列结论中正确的是（ ）
①△ACD≌△BCE；
②△CPQ是等边三角形；
③平分；
④△BPO≌△EDO．
A．①②B．①②③C．①②④D．①②③④
【例2】（2021·江苏·涟水县红日中学八年级阶段练习）如图，点C是线段AE上一动点（不与A，E重合），在AE同侧分别作等边三角形ABC和等边三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ，有以下5个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°．其中一定成立的结论有（ ）个
A．1B．2C．3D．4
【例3】（2020·江苏·靖江市靖城中学八年级期中）如图，点B、C、E在同一条直线上，与都是等边三角形，下列结论：①AE=BD；②；③线段AE和BD所夹锐角为80°；④FG∥BE．其中正确的是______．（填序号）
【例4】（2020·湖南·长沙市长郡外国语实验中学八年级阶段练习）如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作等边三角形ABC和等边三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ．以下结论：①PQAE；②∠AOE＝120°；③CO平分∠BCD；④△CPQ是等边三角形，⑤OC+BO＝AO恒成立的是_____．
【例5】（2022·湖南永州·八年级期末）△ACB和△DCE是共顶点C的两个大小不一样的等边三角形．
(1)问题发现：
如图1，若点A，D，E在同一直线上，连接AE，BE．
①求证：△ACD≌△BCE；
②求∠AEB的度数．
(2)类比探究：如图2，点B、D、E在同一直线上，连接AE，AD，BE，CM为△DCE中DE边上的高，请求∠ADB的度数及线段DB，AD，DM之间的数量关系，并说明理由．
(3)拓展延伸：如图3，若设AD（或其延长线）与BE的所夹锐角为α，则你认为α为多少度，并证明．
六、全等三角形中的动态问题
【例1】★★如图，在Rt△ABC，∠C=90°，AC=12，BC=6，一条线段PQ=AB，P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动，要使△ABC和△QPA全等，则AP= ______ ．
【例2】★★★（2020·广东省绿翠现代实验学校初二期中）如图（1），AB=4，AC⊥AB，BD⊥AB，AC=BD=3．点 P 在线段 AB 上以 1的速度由点 A 向点 B 运动，同时，点 Q 在线段 BD 上由点 B 向点 D 运动．它们运动的时间为 （s）．
（1）若点 Q 的运动速度与点 P 的运动速度相等，当=1 时，△ACP 与△BPQ 是否全等，请说明理由， 并判断此时线段 PC 和线段 PQ 的位置关系；
（2）如图（2），将图（1）中的“AC⊥AB，BD⊥AB”为改“∠CAB=∠DBA=60°”，其他条件不变．设点 Q 的运动速度为，是否存在实数，使得△ACP 与△BPQ 全等？若存在，求出相应的、的值；若不存在，请说明理由．
【亮点训练】
1．（2022·辽宁·沈阳市第一三四中学七年级阶段练习）如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D，若AD=12，CD=5，则ED的长度是（ ）
A．8B．7C．6D．5
2．（2022·广东·西南中学三模）如图，在中，为边上任意一点，按以下步骤作图：①以点为圆心，以任意长为半径作弧，分别交，于点，；②以点为圆心，以长为半径作弧，交于点；③以点为圆心，以长为半径作弧，在内部交前面的弧于点；④作射线交于点若，，则（ ）．
A．B．C．D．
3．（2022·全国·八年级）如图，Rt△ABC中，∠ACB＝90°，∠B＝50°，D，F分别是BC，AC上的点，DE⊥AB，垂足为E，CF＝BE，DF＝DB，则∠ADE的度数为（ ）
A．40°B．50°C．70°D．71°
4．（2022·福建·模拟预测）如图，在正六边形ABCDEF中，点G，H分别是边BC，CD上的点，且，AG交BH于点O，则的度数为（ ）
A．B．C．D．
5．（2021·湖南永州·八年级阶段练习）如图，点在线段上，于，于．，且，，点以的速度沿向终点运动，同时点以的速度从开始，在线段上往返运动（即沿运动），当点到达终点时，，同时停止运动．过，分别作的垂线，垂足为，．设运动时间为，当以，，为顶点的三角形与全等时，的值为（ ）
A．1或3B．1或
C．1或或D．1或或5
6．（2022·山东东营·七年级期末）如图，BE交AC于点M，交CF于点D，AB交CF于点N，，给出的下列五个结论中正确结论的序号为 ．
①；②；③；④；⑤．
7．（2022·山东东营·七年级期末）如图，在中，已知AD是平分线，于点E，，则点D到AB的最短距离是_________．
8．（2022·山东聊城·八年级期末）如图，在四边形中，，，，点在线段上以的速度由点向点运动，同时，点在线段上由点向点运动，设运动时间为，当与以，，为顶点的三角形全等时，点的运动速度为______．
9．（2022·广东·深圳市高级中学八年级期末）如图，把两块大小相同的含45°的三角板ACF和三角板CFB如图所示摆放，点D在边AC上，点E在边BC上，且∠CFE＝13°，∠CFD＝32°，则∠DEC的度数为_______．
10．（2021·全国·八年级期中）如图，在四边形ABCD中，AD＝AB，DC＝BC，∠DAB＝60°，∠DCB＝120°，E在AD上，F是AB延长线上一点，且DE＝BF，若G在AB上，且∠ECG＝60°，则DE、EG、BG之间的数量关系是_____．
11．（2022·全国·八年级）如图，△ABC中，D为BC的中点，
(1)在图中作出CM⊥AD，BN⊥AD，垂足分别为M、N；
(2)求证：DM＝DN；
(3)求AD＝3，求AM＋AN的值．
12．（2022·安徽·合肥寿春中学八年级期末）如图，已知AD是△ABC的边BC上的高，点E为AD上一点，且，．
(1)证明
(2)若，，求△ABC的面积．
13．（2022·全国·八年级）如图，，，，连接，过点作于，过点作于．
(1)若，求的度数；
(2)请直接写出线段、、三者间的数量关系．
14．（2022·辽宁·沈阳市第一三四中学七年级阶段练习）回答问题
（1）【初步探索】如图1：在四边形ABCD中，AB=AD，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且EF=BE+FD，探究图中∠BAE、∠FAD、∠EAF之间的数量关系．
小王同学探究此问题的方法是：延长FD到点G，使DG=BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是_______________；
（2）【灵活运用】如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°．E、F分别是BC、CD上的点，且EF=BE+FD，上述结论是否仍然成立，并说明理由；
（3）【拓展延伸】知在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF=BE+FD，请直接写出∠EAF与∠DAB的数量关系．
15．（2022·云南·景谷傣族彝族自治县教育体育局教研室八年级期末）如图1，点P，Q分别是等边边AB，BC上的动点，点P从顶点A向点B运动，点Q从顶点B向点C运动，两点同时出发，且它们的速度都相同．
(1)连接AQ，CP交于点M则在P、Q运动的过程中，的大小发生变化吗？若变化，则说明理由，若不变，则求出它的度数；
(2)如图2，若点P、Q在运动到终点后继续在射线AB，BC上运动，直线AQ、CP交点为M，则的大小发生变化吗？若变化，则说明理由，若不变，则求出它的度数．
【培优检测】
1．（2021·上海市徐汇中学八年级期中）如图，若 AC、BD、EF两两互相平分于点O，那么图中的全等三角形共有（ ）
A．3对B．4对C．5对D．6对
2．（2022·全国·八年级）如图，AE⊥AB且，BC⊥CD且，请按照图中所标注的数据，计算图中实线所围成的图形的面积是（ ）
A．30B．32C．35D．38
3．（2021·重庆·八年级期中）罗同学学习了全等三角形后，利用全等三角形绘制出了下面系列图案，第（1）个图案由2个全等三角形组成，第（2）个图案由4个全等三角形组成，第（3）个图案由7个全等三角形组成，第（4）个图案由12个全等三角形组成，则第（6）个图案中全等三角形的个数为（ ）
A．25B．38C．70D．135
4．（2021·山东烟台·七年级期中）如图，在四边形ABCD中，AB∥CD，∠B＝90°，∠DAB与∠ADC的平分线相交于BC边上的M点，则下列结论：①∠AMD＝90°；②点M为BC的中点；③AB+CD＝AD；④△ADM的面积是梯形ABCD面积的一半．其中正确的个数有（ ）
A．1个B．2个C．3个D．4个
5．（2020·北京市京源学校八年级期中）如图所示,在中，，AD平分，于点E，则下列结论：①DA平分；②∠=∠；③DE平分∠；④．其中正确的有（ ）
A．①②B．①④C．③④D．①②④
6．（2022·山东烟台·七年级期末）如图，，，F为AB上一点，连接CF，，，垂足分别是点E，D．若，，则DE的长为______cm．

7．（2022·辽宁抚顺·八年级期末）如图，在△AOB和△COD中，OA＝OB，OC＝OD，OA＜OC，∠AOB＝∠COD＝50°，连接AC、BD交于点M，连接OM．下列结论：①AC＝BD，②∠AMB＝50°；③OM平分∠AOD；④MO平分∠AMD．其中正确的结论是 _____．（填序号）
8．（2021·安徽合肥·八年级阶段练习）如图，AE与BD相交于点C，AC＝EC，BC＝DC，AB＝5cm，点P从点A出发，沿A→B方向以2cm/s的速度运动，点Q从点D出发，沿D→E方向以1cm/s的速度运动，P、Q两点同时出发．当点P到达点B时，P、Q两点同时停止运动．设点P的运动时间为t（s）．
（1）AP的长为 ___cm．（用含t的代数式表示）
（2）连接PQ，当线段PQ经过点C时，t＝___s．
9．（2021·全国·八年级单元测试）如图，Rt△ACB中，∠ACB＝90°，△ABC的角平分线AD，BE相交于点P，过点P作PF⊥AD交BC的延长线于点F，交AC于点H，则下列结论：①∠APB＝135°；②BF＝BA；③PH＝PD；④连接CP，CP平分∠ACB．其中正确结论的序号是______．
10．（广东·深圳市高级中学七年级期中）如图，在中，，，，为边上的高，点从点出发在直线上以的速度移动，过点作的垂线交直线于点，当点运动_________时，．
11．（2022·上海·八年级期末）在等腰△OAB和等腰△OCD中，OA＝OB，OC＝OD，连接AC、BD交于点M．
(1)如图1，若∠AOB＝∠COD＝40°：
①AC与BD的数量关系为 ；
②∠AMB的度数为 ．
(2)如图2，若∠AOB＝∠COD＝90°：
①判断AC与BD之间存在怎样的数量关系？并说明理由；
②求∠AMB的度数．
12．（2022·上海·七年级专题练习）阅读：
如图，已知在△ABC和△A′B′C′中，AB＝A′B′，∠A＝∠A′，AC＝A′C′．那么△ABC≌△A′B′C′．
说明过程如下：
把△ABC放到△A′B′C′上，使∠A的顶点与∠A′的顶点重合；由于∠A＝∠A′，因此可以使射线AB、AC分别落在射线A′B′、A′C′上．因为AB＝A′B′，AC＝A′C′，所以点B、C分别与点B′、C′重合，这样△ABC和△A′B′C′重合，即△ABC≌△A′B′C′．
于是，得全等三角形判定方法1：在两个三角形中，如果有两条边及它们的夹角对应相等，那么这两个三角形全等（简记为SAS）．
请完成下面问题的填空：
如图，已知在△ABC和△A′B′C′中，∠A＝∠A′，AB＝A′B′，∠B＝∠B′．
那么△ABC≌△A′B′C′．
说明过程如下：
把△ABC放到△A′B′C′上，因为AB＝A′B′，可以使 与 重合，并使点C与C′在AB（A′B′）的同一侧，这时点A与点A′重合，点 与点 重合．由于∠A＝∠A′，因此射线 与射线 叠合；由于
∠B＝∠B′，因此射线 与射线 叠合．于是点C（射线AC与BC的交点）与点C′（射线A′C′与B′C′的交点）重合．这样 与 重合，即△ABC≌△A′B′C′．
于是，得全等三角形判定方法2：在两个三角形中， ．
13．（2022·甘肃兰州·一模）如图，BD平分∠ABC，点E在BD上．从下面①②③中选取两个作为已知条件，另一个作为结论，构成一个命题，判断该命题真假并说明理由．
①；②；③．
你选择的已知条件是______，结论是______（填写序号）；该命题为______（填“真”或“假”）命题．
注：若选择不同的组合分别解答，则按第一个解答计分．
14．（2021·山西阳泉·八年级期中）通过对下面数学模型的研究学习，解决下列问题：
（1）如图1，∠BAD＝90°，AB＝AD，过点B作BC⊥AC于点C，过点D作DE⊥AC于点E．由∠1+∠2＝∠2+∠D＝90°，得∠1＝∠D．又∠ACB＝∠AED＝90°，可以推理得到△ABC≌△DAE．进而得到AC＝ ，BC＝AE．我们把这个数学模型称为“K字”模型或“一线三等角”模型；
（2）如图2，∠BAD＝∠CAE＝90°，AB＝AD，AC＝AE，连接BC，DE，且BC⊥AF于点F，DE与直线AF交于点G．求证：点G是DE的中点；
（深入探究）
（3）如图，已知四边形ABCD和DEGF为正方形，△AFD的面积为S1，△DCE的面积为S2，则有S1 S2（填“＞、＝、＜”）
15．（2021·河北·廊坊市第四中学八年级阶段练习）如图1，在△ABC中，AE⊥BC于E，AE＝BE，D是AE上一点，且DE＝CE，连接BD，CD．
（1）判断与的位置关系和数量关系，并证明；
（2）如图2，若将△DCE绕点E旋转一定的角度后，BD与AC的位置关系和数量关系是否发生变化？并证明；
（3）如图3，将（2）中的等腰直角三角形都换成等边三角形，其他条件不变，求BD与AC夹角的度数．
一般三角形
直角三角形
判定
边角边（SAS）
角边角（ASA）
角角边（AAS）
边边边（SSS）
两直角边对应相等
一边一锐角对应相等
斜边、直角边定理（HL）
性质
对应边相等，对应角相等（其他对应元素也相等，如对应边上的高相等）
备注
判定三角形全等必须有一组对应边相等
倍长中线
已知：是底边的中线
截长
（将最长线段
一分为二）
四边形ABCD中，BC＞BA，AD=CD，BD平分∠ABC，求证：∠A+∠C=180°
证：在BC上截取AB=A’B，则可证
补短
（将较短线段延长，使其与最长线段相等）
△ABC中，∠C=2∠B，∠1=∠2，求证：AB =AC+CD
证：延长AC至点E，使CE=CD，则可证