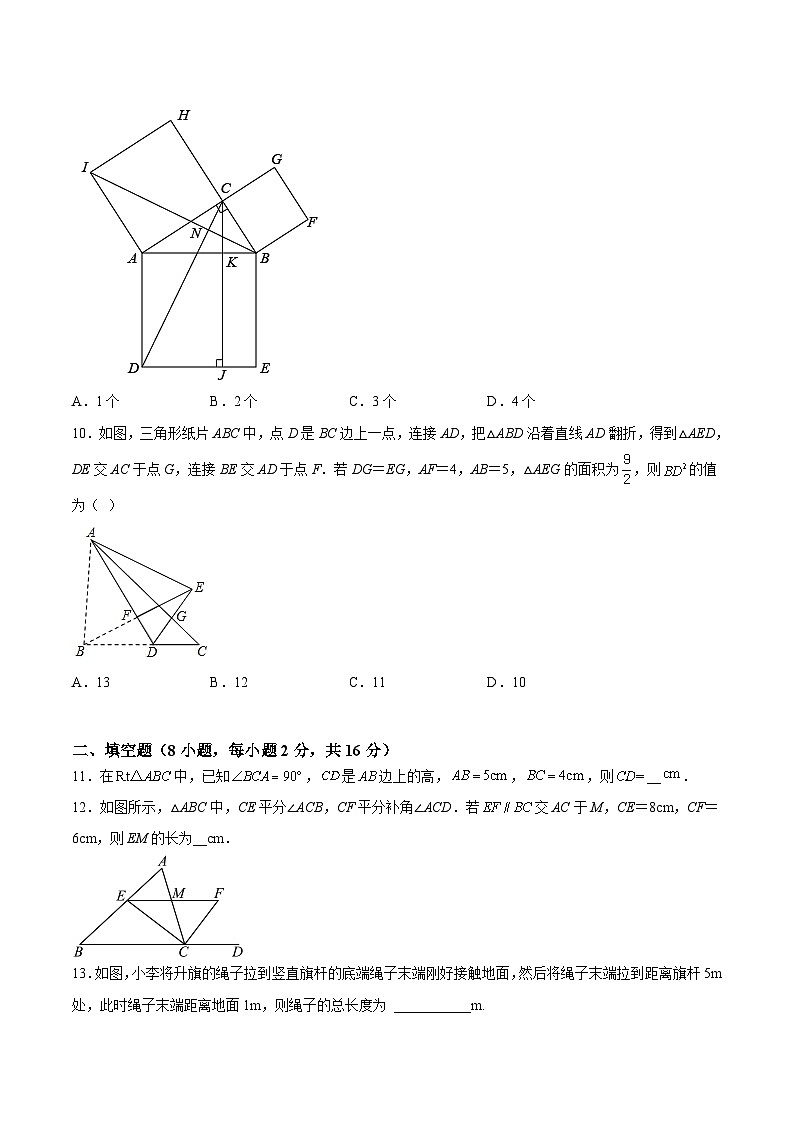
第3章 勾股定理章末复习培优卷-《讲亮点》2022-2023学年八年级数学上册教材同步配套讲练（苏科版）

这是一份第3章 勾股定理章末复习培优卷-《讲亮点》2022-2023学年八年级数学上册教材同步配套讲练（苏科版），文件包含第3章勾股定理章末复习培优卷原卷版docx、第3章勾股定理章末复习培优卷解析版docx等2份试卷配套教学资源，其中试卷共47页， 欢迎下载使用。

第3章 勾股定理章末复习培优卷注意事项：本试卷满分100分，考试时间120分钟，试题共28题。答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置选择题（10小题，每小题2分，共20分）1．下列条件中，一定能判定是直角三角形的是（　　）A． B． C． D．【答案】C【分析】根据三角形的内角和和勾股定理的逆定理判断即可．【详解】A． 当时，，此时，无法求解，故A不是直角三角形；B．当时，设，则，由勾股定理的逆定理可知B不是直角三角形；C． 由勾股定理的逆定理可知C是直角三角形；D．当时，，故D不是直角三角形；故选C．【点睛】本题考查了三角形的内角和和勾股定理的逆定理，熟练掌握直角三角形各边的关系及各角的关系是解题的关键．2．下列各组数中，不是勾股数的是（　　）A． B． C． D．【答案】A【分析】判断是否为勾股数，必须根据勾股数是正整数，同时还需验证两小边的平方和是否等于最长边的平方．【详解】A、，不能构成直角三角形，符合题意；B、，能构成直角三角形，是整数，不符合题意；C、，能构成直角三角形，是整数，不符合题意；D、，能构成直角三角形，是正整数，不符合题意．故选：A．【点睛】本题主要考查了勾股数的定义以及勾股定理的逆定理：已知的三边满足，则是直角三角形．3．如图，ABC中，AB=AC，AD是∠BAC的平分线．已知AB=5，AD=3，则BC的长为（    ）A．8 B．6 C．5 D．4【答案】A【分析】根据等腰三角形的性质得到AD⊥BC，BD=CD，根据勾股定理即可得到结论．【详解】解：∵AB=AC，AD是∠BAC的平分线，∴AD⊥BC，BD=CD，∵AB=5，AD=3，∴，∴BC=2BD=8，故选：A．【点睛】本题考查了勾股定理，等腰三角形的性质，熟练掌握等腰三角形的性质是解题的关键．4．如图，△DEF为等腰三角形，EF=ED，FH⊥ED，DH=2，FH=4，则EF=（    ）A．5 B．6 C．5.5 D．4.5【答案】A【分析】利用等腰三角形的性质结合题干数据表示出EH和EF的关系，再利用勾股定理可以解出EF的长．【详解】解：∵△DEF为等腰三角形，∴EF=ED，∴EH=ED-DH=EF-DH=EF-2，∵FH⊥ED，∴在Rt△EFH中，，又∵FH=4，∴，解得EF=5．故选：A．【点睛】本题考查了等腰三角形和勾股定理，熟练掌握勾股定理和等腰三角形的相关知识是解题的关键．5．我国三国时期数学家赵爽为了证明勾股定理，创造了一幅“弦图”，后人称其为“赵爽弦图”，如图①所示．在图②中，若正方形ABCD的边长为14，正方形IJKL的边长为2，且IJ∥AB，则正方形EFGH的边长为（    ）A．8 B．9 C．10 D．11【答案】C【分析】根据正方形面积公式，由面积的和差关系可得8个直角三角形的面积，进一步得到1个直角三角形的面积，再由面积的和差关系可得正方形EFGH的面积，进一步求出正方形EFGH的边长．【详解】解：一个直角三角形的面积：（14×14−2×2）÷8＝（196−4）÷8＝192÷8＝24，正方形EFGH的面积为：24×4＋2×2＝96＋4＝100，∴正方形EFGH的边长为10．故选：C．【点睛】本题考查了勾股定理的证明，关键是熟练掌握正方形面积公式，以及面积的和差关系，难点是得到正方形EFGH的面积．6．如图，△ABC中，，，O为内一点，且，，则的面积为（    ）A．6 B．4 C．3 D．2【答案】A【分析】延长交于点D，先证出，然后求出，再利用勾股定理得，进而求出，即可求得的面积．【详解】解：延长交于点D，过点O作于点M，作于点N，∵，AO为与公共的底∴与的高相等，即∵，∴是的角平分线∵∴为底边上的高线，即∴在中，利用勾股定理得∴∴的面积：故选A．【点睛】本题考查了等腰三角形和勾股定理的性质，能发现三线合一是解答此题的关键．7．如图，是的角平分线，，，P，D分别是和上的任意一点，连接，，，．给出下列结论：①；②；③的最小值是；④若平分，则的面积为12．其中正确的是（    ）A．①②③ B．①②④ C．②③④ D．①②③④【答案】A【分析】①正确，根据线段的垂直平分线的性质证明即可；②正确，根据两点之间线段最短判断即可；③正确，当CD⊥AB时，PA＋PD的值最小，求出CD的值，即可判断；④错误，△PAH的面积为9．【详解】解：∵BA＝BC，BH是角平分线，∴BH⊥AC，AH＝CH，∴PA＝PC，故①正确， ∴PA＋PD＝PD＋PC≥CD，故②正确，根据垂线段最短可知，当CD⊥AB时，C，P，D共线时，PA＋PD的值最小，最小值为CD，在Rt△ABH中，AB＝10，AH＝AC＝6，，∵，∴CD＝＝，∴PA＋PD的最小值为，故③正确，如图，过点P作PT⊥AB于T，在△PAT和△PAH中，，∴△PAT≌△PAH（AAS），∴AT＝AH＝6，PT＝PH，设PT＝PH＝x,在Rt△PTB中，则有，∴x＝3，∴，故④错误，故选：A．【点睛】本题考查轴对称最短问题，等腰三角形的性质，勾股定理，线段的垂直平分线的性质等知识，解题的关键是证明BH垂直平分线段AC，学会利用参数构建方程解决问题，属于中考常考题型．8．如图，△ABC中，CA＝CB＝15，AB＝18，且则，的值为（    ）A．192 B．291 C．225 D．258【答案】D【分析】延长CO交AB于点M，过点O作OE⊥AC于E，过点O作OF⊥BC于F，利用HL证明△COE≌△COF得∠OCE=∠OCF，从而得出M是AB中点，且CM⊥AB，再根据三角形面积公式以及勾股定理分别求出的长即可求解．【详解】解：如图，延长CO交AB于点M，过点O作OE⊥AC于E，过点O作OF⊥BC于F，∵，AC＝BC，∴OE＝OF，在Rt△COE和Rt△COF中，∴Rt△COE≌Rt△COF（HL），∴∠OCE＝∠OCF，又∵AC＝BC，∴AM＝BM＝9，MC⊥AB，∴＝＝，∴OM＝OC，在Rt△ACM中，AC＝15，AM＝9，∴，即CM＝12（负值舍去），∴OC＝8，OM＝4，  ∴，∴，∴的值为258．故本题选：D．【点睛】本题考查了全等三角形的判定和性质，勾股定理，等腰三角形的性质，熟练掌握勾股定理以及等腰三角形三线合一的性质是解题的关键．9．勾股定理是人类早期发现并证明的重要数学定理之一，是数形结合的重要纽带．数学家欧几里得利用下图验证了勾股定理．以直角三角形ABC的三条边为边长向外作正方形ACHI，正方形ABED，正方形BCGF，连接BI，CD，过点C作CJ⊥DE于点J，交AB于点K．设正方形ACHI的面积为S1，正方形BCGF的面积为S2，矩形AKJD的面积为S3，矩形KJEB的面积为S4，下列结论中：①BI⊥CD；②S1∶S△ACD＝2∶1；③S1－S4＝S3－S2； ④S1S4＝S3S2，正确的结论有（    ）A．1个 B．2个 C．3个 D．4个【答案】D【分析】利用正方形的性质证明△ABI≌△ADC，得出∠AIB=∠ACD，即可得出∠CNI=∠NAI，即可判断①，利用△ABI≌△ADC，即可求出△ABI的面积，即可判断②，由勾股定理和S3+S4=S▱ABED，即可判断③，由③S1-S4=S3-S2，两边平方，根据勾股定理可得，然后计算，即可判断④．【详解】解：∵四边形ACHI和四边形ABED为正方形，∴AI=AC，AD=AB，∠CAI=∠BAD=90°，∵∠BAI=∠BAC+∠CAI，∠DAC=∠BAC+∠BAD，∴∠BAI=∠DAC，∴△ABI≌△ADC（SAS），∴∠AIB=∠ACD，∵∠CNI=∠CAI=90°，∴BI⊥CD，故①正确；∵S△ACD=S△AIB=×AI×AC，S正方形ACHI=S1=AI×AC，∴S1：S△ACD=2：1，故②正确；∵S1=AC2，S2=BC2，S3+S4=S正方形ADEB=AB2，AC2+BC2=AB2，∴S1+S2=S3+S4，∴S1-S4=S3-S2，故③正确； S1-S4=S3-S2，，∵S1=AC2，S2=BC2，S3=AK•KJ= AK•AB，S4=BK•KJ=BK•AB，，，∵AB2=AC2+ BC2，，，即，，∴S1•S4=S2•S3，故④正确，故选D．【点睛】本题考查勾股定理的证明，解题的关键是熟练掌握证明三角形全等的条件，勾股定理的运用，完全平方公式的变形．10．如图，三角形纸片ABC中，点D是BC边上一点，连接AD，把△ABD沿着直线AD翻折，得到△AED，DE交AC于点G，连接BE交AD于点F．若DG＝EG，AF＝4，AB＝5，△AEG的面积为，则的值为（  ）A．13 B．12 C．11 D．10【答案】A【分析】首先根据SAS证明△BAF≌△EAF可得AF⊥BE，根据三角形的面积公式求出AD，根据勾股定理求出BD即可．【详解】解：由折叠得，，∠BAF=∠EAF，在△BAF和△EAF中，，∴△BAF≌△EAF(SAS)，∴BF=EF，∴AF⊥BE，又∵AF＝4，AB＝5，∴，在△ADE中，EF⊥AD，DG＝EG，设DE边上的高线长为h，∴，即，∵，，∴，∴，∴，∴，在Rt△BDF中，，，∴，故选：A．【点睛】本题考查翻折变换、三角形的面积、勾股定理、全等三角形的判定与性质等知识，运用三角形的面积求出AD的长度是解答本题的关键．二、填空题（8小题，每小题2分，共16分）11．在中，已知，是边上的高，，，则__．【答案】【分析】根据勾股定理求出的长，再根据三角形的面积，即可求出的长．【详解】∵是直角三角形∴∴∴∵∴∴．故答案为：．【点睛】本题考查三角形的知识，解题的关键是掌握勾股定理的运用，三角形的面积公式．12．如图所示，△ABC中，CE平分∠ACB，CF平分补角∠ACD．若交AC于M，CE＝8cm，CF＝6cm，则EM的长为__cm．【答案】5【分析】先根据角平分线的定义求出∠ECF=90°，根据勾股定理求出EF的长度，再根据平行线的性质和角平分线的定义可得∠MEC=∠MCE，∠MFC=∠MCF，最后根据等角对等边，即可得EM=CM=FM，即可求解．【详解】解：∵CE平分∠ACB，CF平分补角∠ACD，∴∠MCE=∠BCE=∠ACB，∠FCM=∠FCD=∠ACD，∴∠ECF=∠ACB+∠ACD=(∠ACD+∠ACD)=90°，根据勾股定理可得：cm，∵，∴∠MEC=∠BCE，∠MFC=∠FCD，∴∠MEC=∠MCE，∠MFC=∠MCF，∴EM=CM=FM，∴EM=EF=5cm，故答案为：5．【点睛】本题主要考查了角平分线的定义，平行线的性质以及等腰三角三角形的判定，熟练掌握相关内容是解题的关键．13．如图，小李将升旗的绳子拉到竖直旗杆的底端绳子末端刚好接触地面，然后将绳子末端拉到距离旗杆5m处，此时绳子末端距离地面1m，则绳子的总长度为 ___________m.【答案】13【分析】设旗杆高为，则，过点E作，则四边形是矩形，得到，，在直角三角形中，根据勾股定理计算即可．【详解】如图，设旗杆高为，则，过点E作，则四边形是矩形，所以，，在直角三角形中，，解得，故绳子长为13m，故答案为：13．【点睛】本题考查了勾股定理，矩形的判定和性质，熟练掌握矩形的判定，勾股定理是解题的关键．14．如图：已知在中，，，分别以、为直径作半圆，面积分别记为、，则的值等于__________（结果保留）．【答案】【分析】先由勾股定理可得： 再利用，然后整体代入求解即可.【详解】解：∵，，∴，∵，∴即： 故答案为：【点睛】本题考查的是半圆的面积的计算，勾股定理的应用，掌握利用勾股定理是解题的关键.15．如图，，，，是四根长度均为的火柴棒，点A，C，E共线．，若，则线段的长度是___________．【答案】##8厘米【分析】作BG⊥AC，DH⊥CE，垂足分别为G、H，利用AAS证明△BCG≌△CDH得到BG=CH，利用勾股定理及等腰三角形的性质求出BG=4，再根据等腰三角形的性质即可得出答案．【详解】解：作BG⊥AC，DH⊥CE，垂足分别为G、H，∴∠BGC=∠DHC=90°，∴∠BCG+∠CBG=90°，∵CD⊥BC，∴∠BCD=90°，∴∠BCG+∠DCH=90°，∴∠CBG=∠DCH，在△BCG和△CDH中，，∴△BCG≌△CDH（AAS），∴BG=CH，∵AB=BC，BG⊥AC，AC=6，∴CG=AC=3，∴BM=CN，在Rt△BCG中，由勾股定理得：BG=，∴CH=4，∵CD=DE，DH⊥CE，∴CH=EH，∴CE=CH+EH=8，故答案为：8cm．【点睛】本题主要考查了等腰三角形的性质，勾股定理，正确作出辅助线，证得△BCM≌△CDN是解决问题的关键．16．如图，在四边形ABCD中，∠DAB＝∠BCD＝90°，对角线AC与BD相交于点E，点F，G分别是AC，BD的中点，当∠CBD＝15°，EG＝EC，FG2＝3时，则线段AC的长为________．【答案】6【分析】先连接AG，CG，根据直角三角形的中线性质得AG=CG=BG，再根据等腰三角形的性质和三角形外角的性质得∠EGC，进而求出∠ECG，然后根据含30°角的直角三角形的性质求出，再根据勾股定理求出CF，即可得出答案．【详解】解：如图，连接AG，CG，∵△ABD与△BCD均是BD为斜边的直角三角形，∴AG＝BD，CG＝BD，即AG＝CG=BG，∴△ACG为等腰三角形．∵∠CBD＝15°，CG＝BG，∴∠CGE＝2∠CBD＝30°．∵EC＝EG，∴∠ECG＝∠CGE＝30°．又∵F为AC的中点，∴GF为△ACG的中线，即AF＝CF，∴由“三线合一”知，即∠GFC＝90°，∴CG＝2FG．∵，∴，由勾股定理得：，即CF＝3，∴AC＝2FC＝6．故答案为：6．【点睛】本题主要考查了直角三角形的性质，等腰三角形的性质和判定，勾股定理，三角形的外角性质等，作辅助线构造等腰三角形是解题的关键．17．如图，中，，，，利用尺规在，上分别截取，．使，分别以D，E为圆心，以大于为长的半径作弧，两弧在内交于点F，作射线交边于点G，点P为边上的一动点，则的最小值为______．【答案】##【分析】根据基本作图得到AG平分∠BAC，过G点作GH⊥AB于H，如图，则根据角平分线的性质得到GH＝GC，利用勾股定理计算出AB＝5，再利用面积法求出GH，然后根据垂线段最短解决问题．【详解】解：由作法得AG平分∠BAC，过G点作GH⊥AB于H，如图，∵∠C=90°，即GC⊥AC，∴∠C=90°=∠AHG，∴GH＝GC，∵∠C＝90°，AC＝4，BC＝3，∴，∵，∴，∴GH＝GC，∴5GH+4GH＝12，∴，∵点P为边AB上的一动点，当GP⊥AB时，G点到AB的距离最短，即GP最小，即为，∴GP的最小值为．故答案为：．【点睛】本题考查了作图—角平分线，角平分线的性质，勾股定理，垂线段最短等等，解题的关键在于能够根据题意得到AG平分∠BAC．18．如图，，，，和交于点，点，为边上的两点，且，连接，，则下列结论：①；②；③；④只有当时，，其中正确的有____．（填序号）【答案】①②④【分析】先由，得出，再利用证明，故①正确；由“”可证，得出，进而得出，由勾股定理得出②正确；利用特殊位置可判断，故③错误；由“”可证，可得，故④正确，即可求解．【详解】解：①，，，，在和中，，，故①正确；②由①知，，，，．，，．在与中，，，，在中，由勾股定理得：，，，，故②正确；当点是的中点时，即点与点重合，在中，，，，故③错误；当时，则，又，，，，故④正确；故答案为：①②④．【点睛】本题是三角形综合题，考查了全等三角形的判定和性质，等腰直角三角形的性质，三角形的三边关系，勾股定理等知识，证明三角形全等是解题的关键．三、解答题（10小题，共64分）19．如图，在中，∠BAC=，AB=3，AC=4，AD⊥BC，垂足为D，(1)求BC的长；(2)求AD的长．【答案】(1)5(2)【分析】（1）利用勾股定理列式计算即可得解；（2）利用的面积列式计算即可得解．（1）解：在中，∠BAC=，AB=3，AC=4，∴BC=；（2）解：∵AD⊥BC，∠BAC=，AB=3，AC=4，BC=5，∴，即，∴．【点睛】本题考查了勾股定理，三角形的面积，是基础题，难点在于（2）利用同一个三角形的面积的两种不同表示列出方程．20．等腰三角形有“三线合一”的重要性质，勾股定理是古今中外著名的定理，试用这两个定理或其中的一个定理解答：如图，中，，，                                (1)求的面积；(2)若D是的中点，于E，求出DE的长．【答案】(1)的面积为12；(2)．【分析】（1）过A作于F，由勾股定理易求得此垂线的长，即可求出的面积；（2）连接，由于AD=BD，则、等底同高，它们的面积相等，由此可得到的面积；进而可根据的面积求出的长．（1）解：过A作于F，中，，，，则；中，；由勾股定理，得；∴；（2）解：连接，∵D是的中点，∴；∵，即．【点睛】此题主要考查了等腰三角形的性质、勾股定理、三角形面积的求法等知识的综合应用能力．21．如图，一只蚂蚁在圆柱形玻璃杯的外壁，距高底端2厘米A处发现在自己左上方距离顶端2厘米B处内壁有一滴蜂蜜，已知玻璃杯底面的周长为12厘米，高为8厘米，求蚂蚁吃到蜂蜜的最短距离．【答案】蚂蚁吃到蜂蜜的最短距离为10厘米．【分析】将圆柱体展开，作点B关于圆柱顶的对称点，连接，与圆柱顶交于点D，然后根据勾股定理求解即可．【详解】将圆柱体展开，作点B关于圆柱顶的对称点，连接，与圆柱顶交于点D，根据题意可得，∵玻璃杯底面的周长为12厘米，高为8厘米，∴厘米，厘米，∵厘米，厘米，∴厘米，∵，∴厘米．∴蚂蚁吃到蜂蜜的最短距离为10厘米．【点睛】此题考查了勾股定理的实际应用，解题的关键是根据题意正确画出图形，利用勾股定理求解．22．若的三条边长分别为a，b，c，满足，试说明为直角三角形．【答案】见解析【分析】将原式因式分解可得到 ，进而得出 ，再利用勾股定理的逆定理即可证明出是直角三角形．【详解】证明： 移项得： ，变形得： ，因式分解得： ， ， 解得： ． 是 的三条边，且满足 ，即 ， 是直角三角形．【点睛】本题考查了配方法的应用、勾股定理的逆定理、非负数的性质，解决本题的关键是熟练运用勾股定理的逆定理作出证明．23．如图，小区A与公路l的距离AC＝200米，小区B与公路l的距离BD＝400米，已知CD＝800米，(1)政府准备在公路边建造一座公交站台Q，使Q到A、B两小区的路程相等，求CQ的长；(2)现要在公路旁建造一利民超市P，使P到A、B两小区的路程之和最短，求PA+PB的最小值，并求CP的长度．【答案】(1)475米(2)1000米，米【分析】（1）根据勾股定理列出方程，解方程即可；（2）如图，作点A关于直线l的对称点，连接，交直线l于点P．则AP＝P，AP+BP＝P+BP，PA+PB的最小值为B．（1）解：如图1，此时AQ＝BQ．设CQ＝x，则DQ＝800﹣x，∴，解得x＝475，即CQ的长为475米；（2）解：如图2，作点A关于直线l的对称点，连接，交直线l于点P．则AP＝P，AP+BP＝P+BP，PA+PB的最小值为=1000米．∵，∴，∴，∴CP＝＝＝（米），即CP的长度为米．【点睛】本题考查了轴对称﹣最短路线问题，作图﹣应用与设计作图，坐标与图形的性质，确定出Q、P的位置是本题的关键．24．如图，小颖和她的同学荡秋千，秋千AB在静止位置时，下端离地面0.6m，当秋千荡到AB的位置时（AB=AB/)，下端B距静止位置的水平距离EB等于2.4m，距地面1.4m，求秋千AB的长．（秋千静止时与地面垂直）【答案】4m【分析】设秋千AB的长为x，，可得，根据勾股定理列出方程求解即可．【详解】解：设秋千AB的长为x，离地面0.6m，当秋千荡到AB的位置时距地面1.4m，，，根据勾股定理得：即，解得：， 答：秋千AB的长为4m．【点睛】本题考查了勾股定理的实际应用，根据勾股定理得出相应的方程是解本题的关键．25．如图BE⊥CD，AB＝AD，AC＝AE，过A点作AG⊥DE于G，延长GA交BC于F，(1)求证：F为BC中点；(2)若AF＝12.5，AE＝15，求△ADE的面积．【答案】(1)见解析；(2)150．【分析】（1）证明△ADE≌△ABC （SAS），可得∠DEA＝∠BCA，再证明FC＝FA，然后根据直角三角形两个锐角互余证明FB＝FA，进而可以解决问题；（2）由△ABC≌△ADE知：DE＝BC＝25，利用勾股定理可得AD＝20，进而可以解决问题．（1）证明：∵BE⊥CD，∴∠DAE＝∠DAB＝∠BAC＝∠CAE＝90°，在△ADE和△ABC中，，∴△ADE≌△ABC （SAS），∴∠DEA＝∠BCA，∵AG⊥DE，∴∠AGD＝90°，∴∠AED＋∠ADE＝∠DAG＋∠ADE＝90°，∴∠AED＝∠DAG，∵∠DAG＝∠CAF，∴∠CAF＝∠FCA，∴FC＝FA，∵∠BAC＝90°，∴∠FAC＋∠BAF＝∠FCA＋∠FBA＝90°，∴∠BAF＝∠FBA，∴FB＝FA，∴FB＝FC，∴F是BC的中点；（2）解：∵F为BC的中点，∠BAC＝90°，∴AF＝BC，∴BC＝2AF＝25，由△ABC≌△ADE知：DE＝BC＝25，∵AE＝15，∠DAE＝90°，∴，∴＝×AD•AE＝×20×15＝150．【点睛】本题考查了全等三角形的判定和性质，勾股定理，等腰直角三角形的性质，熟练掌握全等三角形的判定和性质是解题的关键．26．已知，在中，，，点是边上的一点（不与点，重合），连接．(1)如图1，将线段绕点逆时针方向旋转得到线段，连接．求证：，；(2)如图2，点，都在线段上，且．试猜想线段，，之间满足的数量关系，并证明结论．【答案】(1)证明见解析(2)，证明见解析【分析】（1）根据题意，结合，证明，根据全等三角形的性质，得出，，再根据直角三角形两锐角互余，得出，再根据等量代换，得出，进而即可得出结论；（2）根据题意，结合，证明，根据全等三角形的性质，得出，再根据勾股定理，得出，再根据等量代换，即可得出结果．（1）证明：∵，将线段绕点逆时针方向旋转得到线段，∴ ，，∴，在和中，，∴，∴，，∵，∴，∴，∴；（2）解：，理由如下：∵将线段绕点逆时针方向旋转得到线段，，∴，，又∵，∴，∴，∵，∴，由勾股定理得，又∵，∴．【点睛】本题考查了全等三角形的性质与判定、直角三角形两锐角互余、勾股定理，解本题的关键在熟练掌握相关的性质、定理．27．在中，，，P为线段上一动点．(1)如图1，点D、E分别在、上（点D不与点A重合），若P运动到的中点，且．①求证：．②若，，求的长．(2)如图2，点F在上，且，过点F作，垂足为H，若，在点P运动的过程中，线段的长度是否发生变化？若不变，请求出的长度；若变化，请说明理由．【答案】(1)①证明见解析；②(2)的值不变，【分析】（1）①如图1中，连接，根据等腰直角三角形的判定与性质证明，即可证明；②利用全等三角形的性质以及勾股定理可得结论；（2）的值不变，．如图2中，作，垂足为Q，证明，推出，可得结论．（1）①证明：如图1中，连接，∵，，∴为等腰直角三角形，∵P为中点，∴，，，∵，∴，∴，在和中，，∴，∴；②解：如图1中，连接，∵，∴，，∵，∴，∵，，∴，，∴，∵，∴，∵，∴．（2）解：PH的值不变，PH=4．理由：如图2中，作，垂足为Q，∵，∴，∴，∵，，∴，∵，∴，∴，在和中，，∴，∴，∵，，，∴，∴是定值．【点睛】本题属于三角形综合题，考查了等腰直角三角形的性质，全等三角形的判定和性质．直角三角形斜边中线的性质等知识，解题的关键是正确寻找全等三角形解决问题．28．我们定义：在一个图形上画一条直线，若这条直线既平分该图形的面积，又平分该图形的周长，我们称这条直线为这个图形的“等分积周线”．(1)如图，在中，，且，请你在图中用尺规作图作出的一条“等分积周线”；(2)在图中，过点能否画出一条“等分积周线”？若能，说出确定的方法若不能，请说明理由．(3)如图，四边形中，，垂直平分，垂足为，交于点，已知，，求证：直线为四边形的“等分积周线”；(4)如图，在中，cm，cm，请你不过的顶点，画出的一条“等分积周线”，并说明理由．【答案】(1)见解析(2)不能，理由见解析(3)见解析(4)图及理由见解析【分析】（1）作线段的中垂线即可得出答案；（2）若直线平分的面积，那么，得出，进而得出答案；（3）根据勾股定理可得出：，进而得出，，进而得出周长与面积分别相等得出答案即可；（4）在上取一点，使得，在上取一点，使得，作直线，则是的等分积周线，结合全等三角形的判定与性质得出答案．（1）解：如图所示：作线段的中垂线，∵，∴AD=CD， ∴AB+AD=BC+CD，∵，∴，∴直线BD是的一条“等分积周线”；（2）不能，理由：如图，若直线平分的面积，那么，，，，过点不能画出一条“等分积周线”（3）如图3，连接、，设，垂直平分，，，，，，，，和中，根据勾股定理可得出： ，即，解得：，所以，，，∴，∵∴，，，，直线为四边形的“等分积周线”；（4）如图，在上取一点，使得cm，在上取一点，使得cm，作直线，则是的“等分积周线”，理由：由作图可得：cm，在上取一点，使得cm，则有，，， 在和中 ≌（SAS），，∵EG=6-2-2=2cm，∴cm，，，cm，是的“等分积周线”，若如图，当cm，cm时，直线也是的“等分积周线”．其实是同一条，【点睛】此题主要考查了应用与设计作图，全等三角形的判定与性质和勾股定理等知识，根据题意正确分割图形是解题关键．