人教版七年级上册3.1.2 等式的性质教学课件ppt

这是一份人教版七年级上册3.1.2 等式的性质教学课件ppt，共23页。PPT课件主要包含了什么是等式，等式的左边，等式的右边，除以-4，加2n，-2b，除以2，减2x+2，除以3，化简得等内容，欢迎下载使用。
1. 理解、掌握等式的性质. (重点)2. 能正确应用等式的性质解简单的一元一次方程. (难点)
2.下列各式中哪些是等式？
用等号表示相等关系的式子叫做等式. 我们可以用a=b表示一般的等式.
上图是一架天平，现在我把“天平”做为谜面，请你们猜一数学术语.
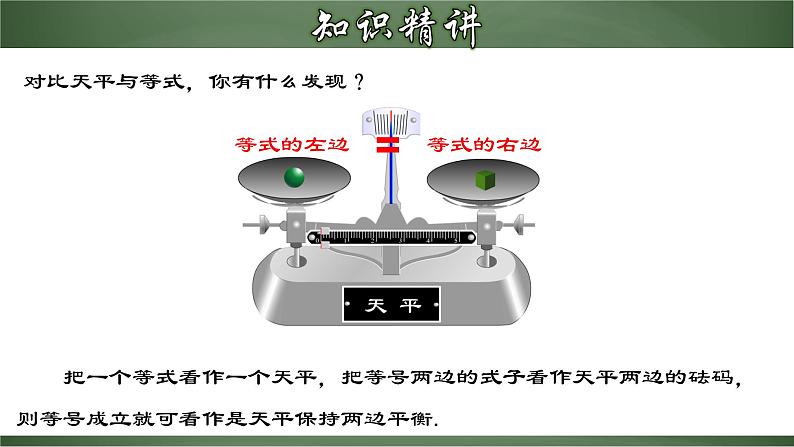
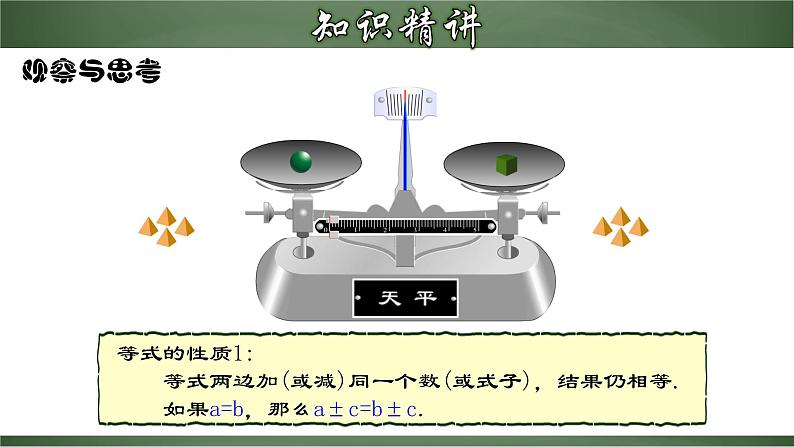
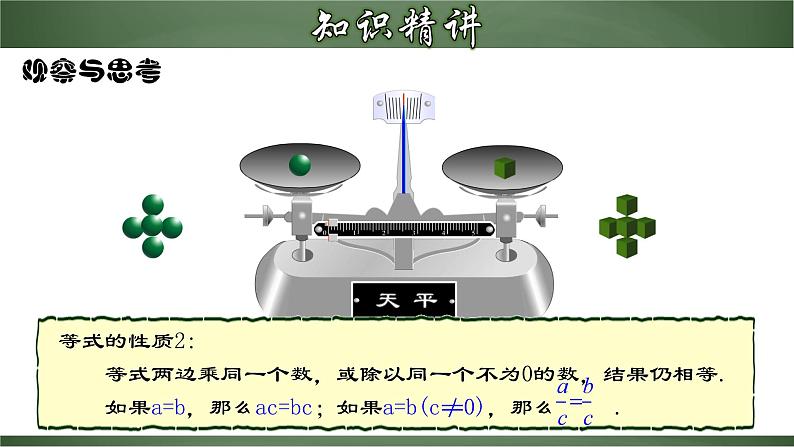
对比天平与等式，你有什么发现？
把一个等式看作一个天平，把等号两边的式子看作天平两边的砝码，则等号成立就可看作是天平保持两边平衡.
例1.用适当的数或式子填空，使所得结果仍是等式，并说明是根据等式的哪一条性质及怎样变形的.(1)若3x+5=8，则3x=8-___，根据等式的性质____，等式的两边_______;(2)若-4x=24，则x=____,根据等式的性质____，等式的两边_________;(3)若m-2n=d-2n，那么m=____,根据等式的性质_____，等式的两边______;(4)若2a=-4b，那么a=_____,根据等式的性质_____，等式的两边________;(5)如果5x+2=2x-4，则3x=____(第一步）,x=_____(第二步),第一步:根据等式的性质___，等式的两边__________,第二步:根据等式的性质_____，等式的两边________.
例2.已知mx=my，下列结论错误的是 （ ）A. x=y B. a+mx=a+my C. mx－y=my－y D. amx=amy
【分析】根据等式的性质1，可知B、C正确；根据等式的性质2，可知D正确；根据等式的性质2，A选项只有m≠0时才成立，故A错误，故选A．
【点睛】此类判断等式变形是否正确的题型中，尤其注意利用等式的性质2等式两边同除某个字母时，只有这个字母确定不为0时，等式才成立.
例3.利用等式的性质解下列方程： (1)x+7=26 (2)－5x=20 (3)
解：方程两边同时减去7，得
x+7-7=26-7
于是 x=19
解：方程两边同时除以－5，得
于是 x=－4
-5x÷(－5)=20÷(－5)
【分析】解以x为未知数的方程，就是把方程逐步转化为x=a(常数)的形式，等式的性质是转化的重要依据.
要使方程x+7=26转化为x=a(常数)的形式，需去掉方程左边的7，利用等式的性质1，方程两边减7就得出x的值. 你可以类似地考虑另两个方程如何转化为x=a的形式.
解：方程两边同时加上5，得
方程两边同时乘-3，得
一般地，从方程解出未知数的值以后，可以代入原方程检验，看这个值能否使方程的两边相等.
方程的左右两边相等，所以x=－27是原方程的解.
例如，将x=－27代入方程的左边，
7.设“ ”“ ”“ ”表示三种不同的物体，现用天平称了两次，情况如图所示，则下列图形不正确的是( )
9.下列结论正确的是( )A.等式3a-6=3b+5两边都除以3，可得等式a-2=b+5B.等式7x=5x+3两边都减去(x-3)，可得等式6x-3=4x+6C.等式-5=0.1x，可得x=-0.5D.等式18+x=0，可得x=-18
15.在解方程3x-3=2x-3时，小华同学是这样解的: 方程两边同加3，得3x-3+3=2x-3+3，(1)，于是3x=2x. 方程两边同除以x，得3=2，(2)所以此方程无解. 小华同学的解题过程是否正确?如果正确，指出每一步的理由;如果不正确，指出错在哪里，并加以改正.
答:小华同学的解题过程第(1)步是正确的，应用了等式的性质1;第(2)步错误，等式的两边只有除以一个不为0的数时，等式才能成立，这里在不确定x是否为0的情况下，方程两边除以x就会导致出错．应改正为:方程两边减2x，得x=0.