初中数学苏科版八年级上册2.5 等腰三角形的轴对称性导学案

这是一份初中数学苏科版八年级上册2.5 等腰三角形的轴对称性导学案，文件包含专题23等腰三角形的性质与判定-《讲亮点》2022-2023学年八年级数学上册教材同步配套讲练苏科版原卷版docx、专题23等腰三角形的性质与判定-《讲亮点》2022-2023学年八年级数学上册教材同步配套讲练苏科版解析版docx等2份学案配套教学资源，其中学案共101页， 欢迎下载使用。

《讲亮点》2022-2023学年八年级数学上册教材同步配套讲练《苏科版》
专题2.3 等腰三角形的性质与判定
【教学目标】
1、理解并掌握等腰三角形的定义，探索等腰三角形的性质和判定方法；
2、利用等腰三角形的性质解决相应数学问题

【教学重难点】
1、理解并掌握等腰三角形的定义，探索等腰三角形的性质和判定方法；
2、利用等腰三角形的性质解决相应数学问题
3、等腰三角形的性质和判定的探索和运用

【知识亮解】
知识点一 等腰三角形的性质
1、等腰三角形
（1）定义：有两条边相等的三角形叫做等腰三角形，相等的两边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。
（2）性质
①两腰相等
②两底角相等（简称等边对等角）
③等腰三角形顶角平分线、底边上的中线、底边上的高线互相重合（简称为“三线合一”）
④等腰三角形是轴对称图形，其顶角平分线、底边上的中线、底边上的高线所在的直线式对称轴。
证明题目中的写法：
①已知高线：∵AB=AC，AD⊥BC，∴BD=CD，∠BAD=∠CAD
②已知中线：∵AB=AC，BD=CD，∴AD⊥BC，∠BAD=∠CAD
③已知角平分线：∵AB=AC，∠BAD=∠CAD，∴AD⊥BC，BD=CD
（3）等腰三角形的构造
（1） “角平分线+平行线”构造等腰三角形
①如下左图所示，OP评分∠AOB，CD∥OA，则△OCD是等腰三角形
②如下右图所示，OP评分∠AOB，CD∥OB，则△OCD是等腰三角形

（2） “角平分线+垂线”构造等腰三角形
如下左图所示，已知AD是∠BAC的平分线，AD⊥BC，得出等腰三角形
（3） “角平分线+中线”构造等腰三角形
如下中图所示，已知AD是∠BAC的平分线，D是BC中点，则△ABC是等腰三角形
（4） “中点+垂直”构造等腰三角形（垂直平分线）如下右图所示

(5)“平行+等腰”构造等腰三角形
已知等腰△ABC，过腰或底上作腰或底的平行线


亮题一 等腰三角形的性质
1．（2022·福建·漳州三中八年级期中）在等腰三角形中，是的高，若，则的底角的度数为（       ）
A．或 B．或 C．或或 D．或或
【答案】B
【解析】
【分析】
根据等腰三角形三线合一的性质可得，从而得到，再利用等边对等角的性质可得，然后利用直角三角形两锐角互余求解即可．
【详解】
解：如图，，，
，
∵，
，
．


如图，当，垂直于延长线，

∵，
∴，
∴，底角为；
当，垂直于，；底角为，
故选：D．
【点睛】
本题考查了等腰三角形三线合一的性质，等边对等角的性质，含30度直角三角形的性质，得出是解题的关键．
2．（2022·黑龙江大庆·中考真题）下列说法不正确的是(     )
A．有两个角是锐角的三角形是直角或钝角三角形
B．有两条边上的高相等的三角形是等腰三角形
C．有两个角互余的三角形是直角三角形
D．底和腰相等的等腰三角形是等边三角形
【答案】A
【解析】
【分析】
利用等腰三角形的性质与判定、等边三角形的性质与判定、直角三角形的判定，对各选项逐项分析可得出正确答案．
【详解】
解：A、设∠1、∠2为锐角，
因为：∠1+∠2+∠3=180°，
所以：∠3可以为锐角、直角、钝角，所以该三角形可以是锐角三角形，也可以是直角或钝角三角形，
故A选项不正确，符合题意；
B、如图，在△ABC中，BE⊥AC，CD⊥AB，且BE=CD．

∵BE⊥AC，CD⊥AB，
∴∠CDB=∠BEC=90°，
在Rt△BCD与Rt△CBE中，
，
∴Rt△BCD≌Rt△CBE（HL），
∴∠ABC=∠ACB，
∴AB=AC，即△ABC是等腰三角形．，
故B选项正确，不符合题意；
C、根据直角三角形的判定：有两个角互余的三角形是直角三角形，，
故C选项正确，不符合题意；
D、底和腰相等的等腰三角形是等边三角形，
故D选项正确，不符合题意；
故选：A．
【点睛】
本题综合考查了等腰三角形的性质与判定、等边三角形的性质与判定、直角三角形的判定，要求学生在学习过程中掌握三角形的各种性质及推论，不断提升数学学习的能力．
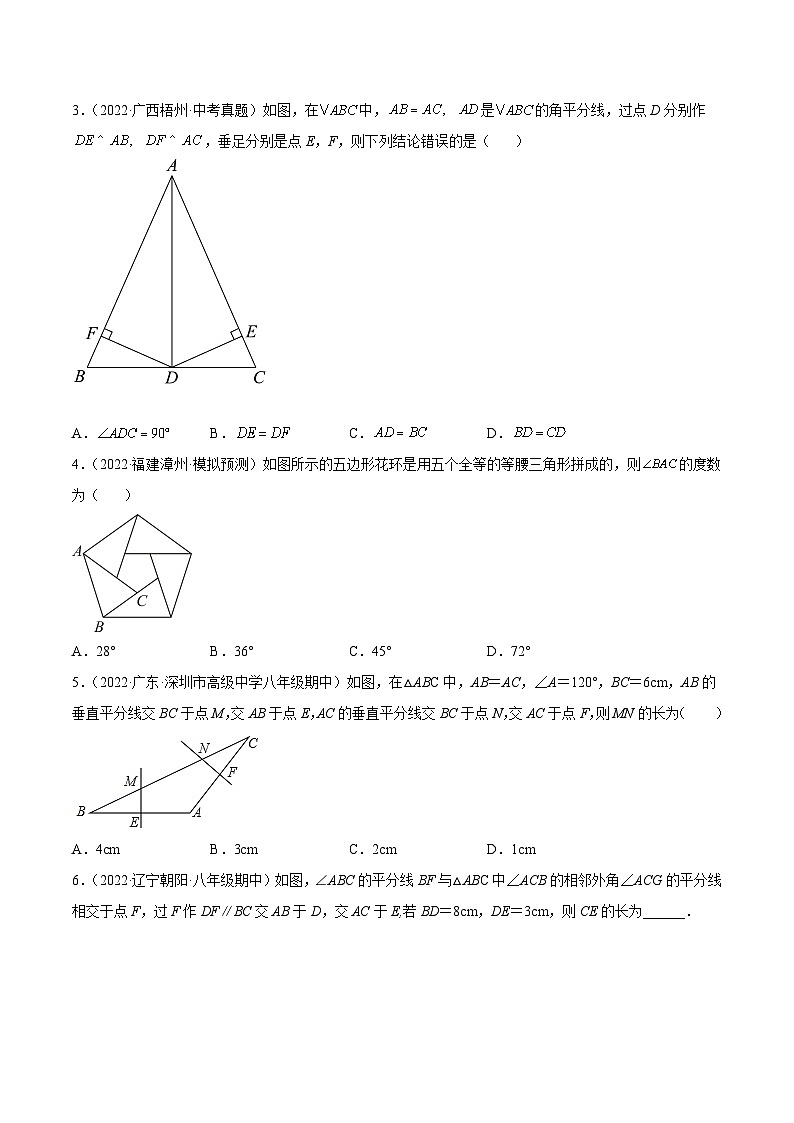
3．（2022·广西梧州·中考真题）如图，在中，是的角平分线，过点D分别作，垂足分别是点E，F，则下列结论错误的是（       ）


A． B． C． D．
【答案】C
【解析】
【分析】
根据等腰三角形底边上的高线、顶角的角平分线、底边上的中线这三线合一及角平分线的性质即可判断求解．
【详解】
解：∵是的角平分线，
∴，
∴，故选项A、D结论正确，不符合题意；
又是的角平分线，，
∴，故选项B结论正确，不符合题意；
由已知条件推不出，故选项C结论错误，符合题意；
故选：C．
【点睛】
本题考察了等腰三角形的性质及角平分线的性质，属于基础题，熟练掌握其性质即可．
4．（2022·福建漳州·模拟预测）如图所示的五边形花环是用五个全等的等腰三角形拼成的，则的度数为（       ）


A．28° B．36° C．45° D．72°
【答案】B
【解析】
【分析】
根据题意可得五个全等的等腰三角形拼成内外两个正五边形，利用正多边形内角和可得∠EAB=∠ACD=，再由邻补角得出∠ACB=∠EAC=，结合图形代入求解即可．
【详解】
解：如图所示，五个全等的等腰三角形拼成内外两个正五边形，


∴∠EAB=∠ACD=，
∴∠ACB=∠EAC=180°，
∴∠BAC=∠EAB-∠EAC =108°，
故选：B．
【点睛】
题目主要考查正多边形内角和及等腰三角形的性质，邻补角等，理解题意，熟练掌握运用正多边形内角和的计算公式是解题关键．
5．（2022·广东·深圳市高级中学八年级期中）如图，在△ABC中，AB＝AC，∠A＝120°，BC＝6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为（　　）

A．4cm B．3cm C．2cm D．1cm
【答案】C
【解析】
【分析】
此类题要通过作辅助线来沟通各角之间的关系，首先求出△BMA与△CNA是等腰三角形，再证明△MAN为等边三角形即可．
【详解】
连接AM，AN，

∵AB的垂直平分线交BC于M，交AB于E，AC的垂直平分线交BC于N，交AC于F，
∴BM=AM，CN=AN，
∴∠MAB=∠B，∠CAN=∠C，
∵∠BAC=120°，AB=AC，
∴∠B=∠C=30°，
∴∠BAM+∠CAN=60°，∠AMN=∠ANM=60°，
∴△AMN是等边三角形，
∴AM=AN=MN，
∴BM=MN=NC，
∵BC=6，
∴MN=2．
故选：C．
【点睛】
本题考查的知识点为线段的垂直平分线性质以及等腰三角形的性质；正确作出辅助线是解答本题的关键．
6．（2022·辽宁朝阳·八年级期中）如图，∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线相交于点F，过F作DF∥BC交AB于D，交AC于E,若BD＝8cm，DE＝3cm，则CE的长为______．

【答案】5cm
【解析】
【分析】
只要证明△BDF和△CEF为等腰三角形，即可解决问题．
【详解】
证明：∵BF、CF分别平分∠ABC、∠ACG，
∴∠DBF＝∠CBF，∠FCE＝∠FCG，
∵DEBC，
∴∠DFB＝∠CBF，∠EFC＝∠FCG，
∴∠DBF＝∠DFB，∠FCE＝∠EFC，
∴BD＝FD，EF＝CE，
∴△BDF和△CEF为等腰三角形；
∴EF＝DF﹣DE＝BD﹣DE＝8﹣3＝5（cm），
∴EC＝5cm．
故答案为：5 cm
【点睛】
本题考查等腰三角形的判定和性质、平行线的性质等知识，解题的关键是证明等腰三角形，属于基础题．
7．（2022·广西·富川瑶族自治县教学研究室模拟预测）如图，在△ABC中，∠ABC=∠ACB，AB的垂直平分线分别交AB、AC于点D、E，连接BE．若AB=5，BC=3，则△BCE的周长是_______．

【答案】8
【解析】
【分析】
根据等角对等边得出，根据线段垂直平分线性质得出AE=BE，然后利用线段的和差转换计算即可．
【详解】
解：∵∠ABC=∠ACB，
∴，
∵DE垂直平分线段AB，
∴AE=BE，
∵BC=3，
∴BC+CE+BE=BC+CE+AE=BC+AC=3+5=8．
故答案为8．
【点睛】
本题主要考查等腰三角形判定与性质，线段垂直平分线的性质，熟练掌握线段垂直平分线的性质定理是解题的关键．
8．（2022·湖南·常德市第七中学八年级期末）等腰三角形的一个外角是100°，则其底角是___________ .
【答案】80°或50°
【解析】
【分析】
等腰三角形的一个外角等于100°，则等腰三角形的一个内角为80°，但已知没有明确此角是顶角还是底角，所以应分两种情况进行分类讨论．
【详解】
解：∵等腰三角形的一个外角等于100°，
∴等腰三角形的一个内角为80°，
①当80°为顶角时，其他两角都为50°、50°，
②当80°为底角时，其他两角为80°、20°，
所以等腰三角形的底角可以是80°或50°，
故答案为：80°或50°．
【点睛】
本题考查了等腰三角形的性质和三角形的内角和定理；在解决与等腰三角形有关的问题时，由于等腰三角形所具有的特殊性质，很多题目在已知不明确的情况下，要进行分类讨论，才能正确解题，因此，解决和等腰三角形有关的边角问题时，要仔细认真，避免出错．
9．（2022·云南文山·二模）如图，在中，，、、分别是边、、上的点，，且，，，则边的长是______．

【答案】13
【解析】
【分析】
根据等腰三角形的性质，可求得∠B=∠C．再证明∠BDE=∠CFD，从而证△EBD≌△DCF，最后求出BC的长即可．
【详解】
解：∵，
∴∠B=∠C，
∵∠CDF+∠EDF+∠BDE=180°，∠CDF+∠C+∠CFD=180°，，
∴∠BDE=∠CFD，
在△EBD和△DCF中
，
∴△EBD≌△DCF（AAS），
∴CD=BE=8，BD=CF=5，
∴BC=BD+CD=5+8=13，
故答案为：13．
【点睛】
此题考查了等腰三角形的性质，全等三角形的判定及性质，此题难度不大，解题的关键是能证明△EBD≌△DCF．
10．（2022·河北·高阳县教育局教研室八年级期末）如图，直线a∥b，点M、N分别为直线a和直线b上的点，连接MN，∠DMN=70°，点P是线段MN上一动点，直线DE始终经过点P，且与直线a、b分别交与点D、E，

（1）当△MPD与△NPE全等时，直接写出点P的位置：___________________；
（2）当△NPE是等腰三角形时，则∠NPE的度数为___________________．
【答案】     MN中点处     70°或40°或55°
【解析】
【分析】
（1）根据全等三角形对应边相等得到MP=NP，即点P是MN的中点；
（2）需要分类讨论：PN=PE、PE=NE、PN=NE．
【详解】
（1）∵a//b
∴∠DMN=∠PNE，∠MDE=∠DEN，
∴当△MPD与△NPE全等时，即△MPD≌△NPE时MP=NP，
即点P是MN的中点．
故答案为：MN中点处
（2）①若PN=PE时，
∵∠DMN=∠PNE=70°，
∴∠DMN =∠PNE=∠PEN=70°．
∴∠NPE=180°-∠PNE-∠PEN=180°-70°-70°=40°．
∴∠NPE =40°；
②若EP=EN时，则∠NPE =∠PNE=∠DMN =70°；
③若NP=NE时，则∠PEN=∠NPE，此时2∠NPE=180°-∠PNE=180°-∠DMN =180°-70°=110°
∴∠NPE =55°；
综上所述，∠NPE的值是40°或70°或55°．
故答案为：40°或70°或55°．
【点睛】
本题考查了等腰三角形的分类讨论，解题关键是理解等腰三角形在没有指明底与腰时需要分类讨论．
11．（2022·全国·八年级）如图在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在边BC上，且∠1＝∠2

(1)说明△ADE≌△BFE的理由；
(2)联结EG，那么EG与DF的位置关系是 　 　，请说明理由．
【答案】(1)见解析
(2)EG⊥DF，见解析
【解析】
【分析】
（1）根据平行线的性质及中点的性质，利用ASA即可求解．
（2）根据角的等量关系可得DG=FG，可得三角形DGF是等腰三角形，由根据全等三角形的性质可得DE=EF，进而可求解．
(1)
解：∵AD∥BC，
∴∠1＝∠F，
∵E是AB的中点，
∴AE＝BE，
在△ADE和△BFE中，
，
∴△ADE≌△BFE（ASA）．
(2)
EG⊥DF，理由如下：

∵∠1＝∠F，∠1＝∠2，
∴∠2＝∠F，
∴DG＝FG，
∴△DGF是等腰三角形，
由（1）知：△ADE≌△BFE，
∴DE＝EF，
∴EG⊥DF，
故答案为：EG⊥DF．
【点睛】
本题主要考查了全等三角形的判定与性质，以及等腰三角形的三线合一等知识，找出全等所需的条件是解题的关键．
12．（2022·广东·佛山市惠景中学三模）如图，在△ABC中，BD⊥AC，垂足为D．

(1)请用直尺和圆规按下列要求作图：过点C作AB的垂线CM，交AB边于点F：（不写作法，保留作图痕迹）
(2)在（1）问图中，若BD=CF，求证：△ABC为等腰三角形．
【答案】(1)见解析
(2)见解析
【解析】
【分析】
（1）按照尺规作图作垂线的方法作答即可；
（2）证明Rt△BFC≌Rt△CDB即可．
(1)
作图如下：

作图方法：以C为圆心、BC为半径作弧交AB于点N，再分别与B、N为圆心，以大于BN一半的长度画弧，两弧交于点M，连接CM，交AB于点F，即CM即为所求．
∵CM是线段BN的垂直平分线，
∴CM⊥AB；
即CM即为所求；
(2)
证明∵BD⊥AC，CF⊥AB，
∴∠BFC=∠BDC=90°，
则在Rt△BFC和Rt△CDB中，有BC=BC，BD=CF，
∴Rt△BFC≌Rt△CDB，
∴∠B=∠C，
∴AB=AC，
∴△ABC是等腰三角形．
【点睛】
本题考查了尺规作图---作垂线，还考查了全等三角形的判定与性质，掌握尺规作图做垂线的方法是解答本题的关键．
13．（2022·辽宁朝阳·八年级期中）已知：如图，在△ABC中，∠C＝90°，AE是△ABC的角平分线；ED平分∠AEB，交AB于点D；∠CAE＝∠B．

(1)求∠B的度数．
(2)如果AC＝3cm，求AB的长度．
(3)猜想：ED与AB的位置关系，并证明你的猜想．
【答案】(1)30°
(2)6cm
(3)ED⊥AB，理由见解析
【解析】
【分析】
（1）先由角平分线的定义及已知条件得出∠CAE＝∠EAB＝∠B，再根据直角三角形两锐角互余得出∠CAE＋∠EAB＋∠B＝3∠B＝90°，那么∠B＝30°；
（2）根据30°角所对的直角边等于斜边的一半得出AB＝2AC＝6cm；
（3）先由∠EAB＝∠B，根据等角对等边得出EB＝EA，又ED平分∠AEB，根据等腰三角形三线合一的性质得到ED⊥AB．
(1)
∵AE是△ABC的角平分线，
∴∠CAE＝∠EAB，
∵∠CAE＝∠B，
∴∠CAE＝∠EAB＝∠B．
∵在△ABC中，∠C＝90°，
∴∠CAE＋∠EAB＋∠B＝3∠B＝90°，
∴∠B＝30°；
(2)
∵在△ABC中，∠C＝90°，∠B＝30°，AC＝3cm，
∴AB＝2AC＝6cm；
(3)
猜想：ED⊥AB．理由如下：
∵∠EAB＝∠B，
∴EB＝EA，
∵ED平分∠AEB，
∴ED⊥AB．
【点睛】
本题考查了含30度角的直角三角形的性质：在直角三角形中，30°角所对的直角边等于斜边的一半．直角三角形两锐角互余的性质，等腰三角形三线合一的性质，等腰三角形的判定，熟记性质与判定定理是解题的关键．
14．（2020·湖南·常德市第七中学八年级期中）如图，△ABC中，AD⊥BC，点E在AC的垂直平分线上，且BD=DE．

(1)如果∠BAD = 20°，求∠B的度数，求∠C 的度数；
(2)如果△ABC的周长为13 cm，AC = 6 cm，求△ABE的周长；
【答案】(1)∠B＝70°，∠C＝35°；
(2)△ABE的周长为7cm；
【解析】
【分析】
（1）根据线段垂直平分线的性质求出AB=AE，根据等腰三角形的性质可求∠B＝∠AEB，再根据三角外角的性质求出∠C即可；
（2）通过线段的等量代换即可求解．
(1)
解：∵AD⊥BC，BD=DE，
∴AD垂直平分BE，
∴AB＝AE，
∴∠BAD＝∠EAD＝20°，
∴∠BAE＝40°，
∴∠AEB＝∠B＝，
∵点E在AC的垂直平分线上，
∴AE=EC，
∴∠C=∠EAC=∠AEB=35°；
(2)
解：∵△ABC的周长为13cm，AC=6cm，
∴AB+BC=13-6=7(cm)，
∴△ABE的周长=AB+BE+AE= AB+BE+EC=AB+BC=7(cm)．
【点睛】
本题考查了等腰三角形的性质，线段垂直平分线的性质，三角形外角性质的应用，主要考查学生综合运行性质进行推理和计算的能力．
15．（2022·浙江温州·中考真题）如图，是的角平分线，，交于点E．


(1)求证：．
(2)当时，请判断与的大小关系，并说明理由．
【答案】(1)见解析
(2)相等，见解析
【解析】
【分析】
（1）利用角平分线的定义和平行线的性质可得结论；
 （2）利用平行线的性质可得， 则AD= AE，从而有CD = BE，由(1) 得，，可知BE = DE，等量代换即可．
(1)
证明：∵是的角平分线，
∴．
∵，
∴，
∴．
(2)
．理由如下：
∵，
∴．
∵，
∴，
∴，
∴，
∴，即．
由（1）得，
∴，
∴．
【点睛】
本题主要考查了平行线的性质，等腰三角形的判定与性质，角平分线的定义等知识，熟练掌握平行与角平分线可推出等腰三角形是解题的关键．



知识点二 等腰三角形的判定
等腰三角形的判定
等腰三角形的判定
①有两条边相等的三角形是等腰三角形。
②有两个角相等的三角形是等腰三角形。（简称“等角对等边”）
总结：

亮题二 等腰三角形的性质
1．（2022·陕西延安·八年级期末）如图，在中，，直线DE，FG分别是AB，AC的垂直平分线，则的度数为（       ）

A．80° B．70° C．65° D．60°
【答案】A
【解析】
【分析】
根据线段垂直平分线的性质证明∠EAB=∠B，∠FAC=∠C，由三角形内角和定理求出∠B+∠C=180°-∠BAC=50°，则∠EAB+∠FAC=50°，再由∠BAC=∠EAF+∠EAB+∠FAC，即可得到∠EAF=80°．
【详解】
解：∵DE，FG分别是AB，AC的垂直平分线，
∴EB=EA，FA=FC，
∴∠EAB=∠B，∠FAC=∠C，
∵∠BAC=130°，
∴∠B+∠C=180°-∠BAC=50°，
∴∠EAB+∠FAC=50°，
又∵∠BAC=∠EAF+∠EAB+∠FAC，
∴∠EAF=80°，
故选A．
【点睛】
本题主要考查了线段垂直平分线的性质，等边三角形的性质与判定，三角形内角和定理，熟知线段垂直平分线的性质是解题的关键．
2．（2022·河北秦皇岛·八年级期末）如图，已知在△ABC中，∠ACB＝90°，∠A＝60°，AC＝4，点M，N在边AB上，CM＝CN．若MN＝2，则AM＝(          )

A．1 B．2 C．3 D．4
【答案】A
【解析】
【分析】
过点C作CD⊥AB于点D，根据∠A=60°，得到∠ACD=30°，则有AD=AC，在等腰△CMN中，CD⊥MN，CM=CN，则有MD=ND，即可求出AM．
【详解】
过点C作CD⊥AB于点D，如图，

∵CD⊥AB，∠A=60°，
∴在Rt△ACD中，有∠ACD=30°，
∴ AD=AC，
又∵AC=4，
∴ AD=2，
∵△MCN中，CM=CN，CD⊥AB，
∴CD是等腰△CMN底边的中线，
∴MD=ND=MN，
又∵MN=2，
∴MD=1，
∴AM=AD-MD=2-1=1，
故选：A．
【点睛】
本题考查了含特殊角的直角三角形的性质和等腰三角形的判定和性质．过C点作AB的垂线是解答本题的关键．
3．（2022·湖南邵阳·八年级期末）如图，中，DE是线段AC的垂直平分线，且分别交BC，AC于点D，E，，，则（       ）

A．40° B．45° C．50° D．55°
【答案】B
【解析】
【分析】
根据线段垂直平分线的性质得出AD=CD，求出∠DAC的度数，根据三角形内角和定理求出∠BAC，即可得出答案．
【详解】
∵DE是AC的垂直平分线且分别交BC， AC于点D和E，
∴AD= CD，
∴∠C=∠DAC，
∵∠C= 40°，
∴∠DAC= 40°，
在△ABC中，∠B= 55°，∠C= 40°，
∴∠BAC= 180°-∠B-∠C= 85° ，
∴∠BAD=∠BAC-∠DAC= 85°- 40°=45°
故选：B．
【点睛】
本题考查了线段垂直平分线的性质、等腰三角形的性质和三角形内角和定理等知识点，能求出AD = CD是解此题的关键．
4．（2022·辽宁本溪·八年级期中）如图，已知，平分，点，，分别是射线，，上的动点（，不与点重合）连接，连交射线于点，且，当是等腰三角形时，则的度数为（       ）

A．或或 B．或 C．或 D．或
【答案】C
【解析】
【分析】
分两种情况：①当，即时，②当，即时，运用平行线的性质以及角平分线的定义，可得的度数，根据、的度数以及的内角和即可求解．
【详解】
解：∵，OE平分，
∴．
∵，
∴，
当，即时，
∵，
∴．
∵，
∴，
∴；
当，即时，
∵，，
∴．
∵，
∴．
综上所述，的度数为或．
故选：C．
【点睛】
本题考查了等腰三角形的性质，三角形的内角和定理和平行线的性质的应用，利用平行线以及角平分线的性质求出的度数是关键，注意分类讨论思想的运用．
5．（2022·甘肃武威·八年级期中）如图，在四边形ABCD中，，，，E是AC的中点，连接BE，BD，则的度数为（        ）

A．15° B．14° C．12° D．10°
【答案】A
【解析】
【分析】
连接，根据直角三角形的性质可得，，，从而得到为等边三角形，，由等腰三角形的性质可得，，得到，即可求解．
【详解】
解：连接，如下图：

∵，E是AC的中点，
∴，
又∵，，
∴，
∴，为等边三角形，
∴，，
∴，
又∵，
∴，
故选：A
【点睛】
此题考查了直角三角形的性质，等边三角形的判定与性质，等腰三角形的性质，熟练掌握相关性质是解题的关键．
6．（2022·浙江绍兴·中考真题）如图，在中，，，以点为圆心，长为半径作弧，交射线于点，连接，则的度数是______．

【答案】10°或100°
【解析】
【分析】
分两种情况画图，由作图可知得，根据等腰三角形的性质和三角形内角和定理解答即可．
【详解】
解：如图，点即为所求；

在中，，，
，
由作图可知：，
，
；
由作图可知：，
，
，
，
．
综上所述：的度数是或．
故答案为：或．
【点睛】
本题考查了作图复杂作图，三角形内角和定理，等腰三角形的判定与性质，解题的关键是掌握基本作图方法．
7．（2022·河北保定·一模）将一副三角尺如图所示叠放在一起，若，则

（1）________；
（2）阴影部分的面积是________．
【答案】     4     8
【解析】
【分析】
（1）利用含30°角的直角三角形的性质，就可以得出结果；
（2）证得阴影部分是等腰直角三角形就可以求出其面积．
【详解】
解：（1）由图可知：在中，，
∴．
∵cm，
∴cm．
故答案为：4．
（2）由图可知：，
∴，
∴．
又∵，
∴是等腰直角三角形，
∴ ．
由（1）知：cm，
∴cm．
∴阴影部分的面积为：．
故答案为：8．
【点睛】
本题考查了含30°角的直角三角形中30°角所对的直角边是斜边的一半、等腰直角三角形，平行线的性质与判定、直角三角形的面积公式等知识．正确运用含30°的直角三角形的性质和判断出阴影部分是等腰直角三角形是解决本题的关键．
8．（2022·贵州毕节·一模）如图，P为△ABC边BC上的一点，且PC＝2PB，已知∠ABC＝45°，∠APC＝60°，则∠ACB的度数是 _____°．

【答案】75
【解析】
【分析】
过C作AP的垂线CD，垂足为点D．连接BD，根据三角形内角和定理求出∠DCP＝30°，求证PB＝PD；再根据三角形外角性质求证BD＝AD，再利用△BPD是等腰三角形，然后可得AD＝DC，∠ACD＝45°从而求出∠ACB的度数．
【详解】
解：过C作AP的垂线CD，垂足为点D．连接BD，


∵△PCD中，∠CDP＝90°，∠APC＝60°，
∴∠DCP＝90°－∠APC＝30°，
∴PC＝2PD，
∵PC＝2PB，
∴BP＝PD，
∴△BPD是等腰三角形，
∴∠BDP＝∠DBP，
∵∠BDP＋∠DBP＝∠APC＝60°，
∴∠BDP＝∠DBP＝30°，
∵∠ABP＝45°，
∴∠ABD＝∠ABP－∠DBP＝15°，
∵∠BAP＝∠APC﹣∠ABC＝60°﹣45°＝15°，


∴∠ABD＝∠BAD＝15°，
∴BD＝AD，
∵∠DBP＝30°，∠DCP＝30°，
∴BD＝DC，
∴△BDC是等腰三角形，
∵BD＝AD，
∴AD＝DC，
∵∠CDA＝90°，
∴△ADC是等腰直角三角形，
∴∠ACD＝45°，
∴∠ACB＝∠DCP+∠ACD＝75°，
故答案为：75．
【点睛】
此题主要考查三角形内角和定理，等腰三角形的判定与性质，三角形外角的性质等知识点，添加适当的辅助线是解解决此题的关键．
9．（2022·江苏南京·一模）如图，在正五边形ABCDE中，M是AB的中点，连接AC，DM交于点N，则∠CND的度数是 _____．

【答案】
【解析】
【分析】
连接BD，AD，根据正五边形的性质得到AB＝BC＝CD＝AE＝DE，∠BCD＝∠E，∠ABC＝108°，证明△BCD≌△AED，根据全等三角形的性质得到BD＝AD，根据等腰三角形的性质得到DM⊥AB，求得∠AMN＝90°，于是得到结论．
【详解】
解：连接BD，AD，
在正五边形ABCDE中，AB＝BC＝CD＝AE＝DE，∠BCD＝∠E，∠ABC＝＝108°，
∴＝36°，
在△BCD与△AED中，，
∴△BCD≌△AED（SAS），
∴BD＝AD，
∵M是AB的中点，
∴BM＝AM，
∴DM⊥AB，
∴∠AMN＝90°，
∴∠CND＝∠ANM＝90°﹣36°＝54°，
故答案为：54°．

【点睛】
本题考查了正多边形，全等三角形的判定和性质，等腰三角形的性质，正确地作出辅助线是解题的关键．
10．（2022·上海·七年级单元测试）如图，在△ABC中，∠ABC和∠ACB的角平分线相交于点D，过点D作DE∥AB交BC于点E，DF∥AC交BC于点F，若BC＝a，AB＝c，AC＝b，则△DEF的周长为_____．

【答案】a
【解析】
【分析】
根据角平分线的定义可得∠ABD＝∠EBD，再根据两直线平行，内错角相等可得∠ABD＝∠EDB，然后求出∠EBD＝∠EDB，根据等角对等边的性质可得BE＝DE，同理可得CF＝DF，然后求出△DEF的周长＝BC，代入数据即可得解．
【详解】
解：∵BD平分∠ABC，
∴∠ABD＝∠EBD，
∵DE∥AB，
∴∠ABD＝∠EDB，
∴∠EBD＝∠EDB，
∴BE＝DE，
同理可得：CF＝DF，
∴△DEF的周长＝DE+EF+DF＝BE+EF+CF＝BC，
∵BC＝a，
∴△DEF的周长＝a．
故答案为：a．
【点睛】
本题考查了等腰三角形的性质与判定，主要利用了角平分线的定义，平行线的性质，等角对等边的性质，是基础题，熟记性质是解题的关键．
11．（2022·浙江·金华市第九中学九年级阶段练习）如图，在四边形ABCD中，AB＝DC，∠B＝∠C，E，F是边BC上的两点，且BE＝CF．


(1)求证：△ABF≌△DCE．
(2)若∠APE＝70°，求∠ADP的度数．
【答案】(1)见解析
(2)35°
【解析】
(1)
证明：∵BE=CF，
∴BE+EF=CF+EF，
即BF=CE，
在△ABF和△DCE中，

∴△ABF≌△DCE；
(2)
∵△ABF≌△DCE，
∴AF=DE，∠AFB=∠DEC，
∴PE=PF，
∴AF-PF=DE-PE，
即PA=PD，
∴∠PAD=∠PDA，
又∵∠APE=∠PAD+∠PDA，
∴∠PDA=∠APE=35°．
【点睛】
本题考查全等三角形的判定和性质以及等腰三角形的判定和性质，利用全等三角形的性质得到∠PAD=∠PDA是解决问题的关键．
12．（2022·河北唐山·八年级期末）已知：如图，在中，，，，垂足分别为D、E，与交于点O．

发现：与有何数量关系？并说明理由；
探索：判断的形状，并说明理由；
拓展：连接并延长，交于点F，请你直接写出一条关于的结论．
【答案】发现：BD=CE，理由见详解；
探索：△BOC是等腰三角形，理由见详解；
拓展：AF⊥BC，理由见详解（或者AF平分∠BAC，证明过程同AF⊥BC的证明过程）
【解析】
【分析】
（1）利用AAS定理证明，即可得BD=CE；
（2）结合“发现”中已经证得，可知∠DBC=∠ECB，即有有OC=OB，即△BOC是等腰三角形；
（3）在“探索”中已经证得BO=CO，即根据AB=AC，AO=AO，得，则有∠EAO=∠DAO，再结合AB=AC，AF=AF，得，即有∠AFB=∠AFC=90°，即可得AF⊥BC．
【详解】
发现：BD=CE，理由如下：
∵AB=AC，
∴∠ABC=∠ACB，
又∵BD⊥AC，CE⊥AB，
∴∠CEB=∠BDC=90°，
又有BC=CB，
∴，
∴BD=CE，
得证；
探索：△BOC是等腰三角形，理由如下：
在“发现”中已经证得，
∴∠DBC=∠ECB，
∴有OC=OB，即△BOC是等腰三角形，
得证；
拓展：AF⊥BC，
理由如下：
如图：

在“探索”中已经证得BO=CO，
又∵AB=AC，AO=AO，
∴，
∴∠EAO=∠DAO，
∴AF平分∠BAC，
又∵AB=AC，AF=AF，
∴，
∴∠AFB=∠AFC=90°，
∴AF⊥BC．
【点睛】
本题主要考查了全等三角形的判定和性质、等腰三角形的判定和性质、角平分线的判定等知识，掌握全等三角形的判定和性质是解答本题的关键．
13．（2021·浙江温州·一模）我们把端点都在格点上的线段叫做格点线段，如图，在6×6的方格纸中，有一格点线段AB，请按要求画图．

(1)在图1中画格点线段AC，BC，使得AC⊥BC．
(2)在图2中画一格点线段EF，使得EF将AB平分，并且与AB的夹角是45°．
【答案】(1)见解析
(2)见解析
【解析】
【分析】
（1）根据题意画出图形即可（答案不唯一）；
（2）利用等腰直角三角形的性质，构建图形即可；
(1)
解：如图1中，点C，点C′，点C″即为所求（答案不唯一）．
；
(2)
解：如图2中，线段EF即为所求．
．
【点睛】
本题考查作图-应用与设计作图，等腰三角形的判定和性质，解题的关键是学会利用数形结合的思想解决问题．
14．（2022·辽宁辽宁·二模）综合与实践：


(1)问题发现如图1，和均为等边三角形，点A，D，E在同一直线上，连接BE．请写出的度数及线段之间的数量关系，并说明理由．
(2)类比探究：如图2，和均为等腰直角三角形，，点A，D，E在同一直线上，CM为中DE边上的高，连接BE．
填空：①的度数为_______；
②线段之间的数量关系为_________，并说明理由．
(3)拓展延伸；在（2）的条件下，若，求四边形ABEC的面积．
【答案】(1)∠AEB=60°，AD=BE，理由见解析
(2)①90°，②AE=BE+2CM，理由见解析
(3)35
【解析】
【分析】
（1）先得出∠ACD=∠BCE，进而用SAS判断出△ACD≌△BCE，即可得出结论；
（2）①同（1）的方法，即可得出结论；
②由△ACD≌△BCE得出AD=BE，再判断出DM=CM，即可得出结论．
（3）根据（2）的结论求得AE＝10，再根据四边形ABEC的面积＝△ACE的面积+△ABE的面积，通过计算即可求解．
(1)
解：∵△ACB和△DCE是等边三角形，
∴CA=CB，CD=CE，∠ACB=∠DCE=60°，
∴∠ACD=∠BCE，
在△ACD和△BCE中，
，
∴△ACD≌△BCE（SAS），
∴∠ADC=∠BEC，AD=BE，
∵△CDE是等边三角形，
∴∠CDE=∠CED=60°，
∴∠ADC=180°-∠CDE=120°，
∴∠BEC=120°，
∴∠AEB=∠BEC-∠CED=120°-60°=60°；
(2)
解：同（1）的方法得，△ACD≌△BCE（SAS），
∴∠ADC=∠BEC，
∵△DCE是等腰直角三角形，
∴∠CDE=∠CED=45°，
∴∠ADC=180°-∠CDE=135°，
∴∠BEC=135°，
∴∠AEB=∠BEC-∠CED=135°-45°=90°；
②∵△ACD≌△BCE，
∴AD=BE，
∵CD=CE，CM⊥DE，
∴DM=ME，
在Rt△DCE中，CM⊥DE，∠CDM=45°，
∴∠DCM=∠CDM=45°，
∴DM=CM，
∴DM=ME=CM，
∴AE=AD+DE=BE+2CM．
(3)
解：由（2）得：∠AEB=90°，AD=BE=4，
∵△DCE均为等腰直角三角形，CM为△DCE中DE边上的高，
∴CM⊥AE，∠CDE=∠CED=45°，
∴∠CDE=∠CED=∠DCM=∠ECM=45°，
∴CM=DM=ME，
∴DE＝2CM＝6，
∴AE＝AD+DE＝4+6＝10，
∴四边形ABEC的面积＝△ACE的面积+△ABE的面积
＝AE×CM+AE×BE
＝×10×3+×10×4
＝35；
故答案为：35．
【点睛】
本题主要考查了等边三角形的性质，全等三角形的判定和性质，直角三角形的性质，等腰直角三角形的性质，判断出△ACD≌△BCE是解本题的关键．
15．（2022·广东·江门市第二中学八年级开学考试）已知，在△ABC中，∠BAC＝2∠B，E是AB上一点，AE＝AC，AD⊥CE，垂足为D，交BC于点F．

(1)如图1，若∠BCE＝30°，试判断△ABC的形状，并说明理由；
(2)如图2，若AD＝4，求BC的长．
【答案】(1)△ABC为直角三角形，理由见解析
(2)8
【解析】
【分析】
（1）根据已知求得∠BAD＝∠CAD＝∠B，由∠BCE＝30°，∠CDF＝90°，求得∠AFC＝∠B+∠BAF＝60°，即可求出∠ACD＝60°，得到△ABC为直角三角形；
（2）过C作CG∥AB交AD的延长线于点G．于是得到∠B＝∠BCG，∠BAF＝∠CAF＝∠G，求得∠BCG＝∠G，根据等式的性质得到AG＝BC，根据直角三角形的性质即可得到结论．
(1)
解：△ABC为直角三角形，理由如下：
∵AE＝AC，AD⊥CE，
∴∠ADC＝∠CDF＝90°，
∴∠BAC＝2∠EAD＝2∠CAD，
又∵∠BAC＝2∠B，
∴∠BAD＝∠CAD＝∠B，
∵∠BCE＝30°，∠CDF＝90°，
∴∠AFC＝∠B+∠BAF＝60°，
∴∠BAF＝∠B＝∠CAD＝30°，
∵∠ADC＝90°，
∴∠ACD＝60°，
∴∠BCA＝90°，
即△ABC为直角三角形；
(2)
如图2，过C作CG∥AB交AD的延长线于点G．

则：∠B＝∠BCG，∠BAF＝∠CAF＝∠G，
又∵∠BAF＝∠B，
∴∠BCG＝∠G，
∴CA＝CG，FA＝FB，FC＝FG，
∴AG＝BC，
在△ACG中，CA＝CG，AG⊥CD，
∴AG＝2AD＝2DG，
∴BC＝2AD，
∵AD＝4，
∴BC＝2AD＝8．
【点睛】
此题考查了等腰三角形的判定和性质，直角三角形的判定和性质，正确作出辅助线是解题的关键．



【亮点训练】
1．（2022·云南临沧·八年级期末）如图，在Rt△ABC中，斜边AB的垂直平分线交边AB于点E，交边BC于点D，如果∠ABC=26°，那么∠CAD的度数为（     ）

A．26° B．38° C．64° D．32°
【答案】B
【解析】
【分析】
根据线段垂直平分线的性质可得，再利用等腰三角形的性质和直角三角形两锐角互余即可求解．
【详解】
解：∵斜边AB的垂直平分线交边AB于点E，交边BC于点D，
∴，
∴，
∴，
故选：B．
【点睛】
本题考查线段垂直平分线的性质，线段垂直平分线上的点到线段两个端点的距离相等．
2．（2022·山东临沂·八年级期末）如图，E为△ABC内一点，BE平分∠ABC，CD⊥BE，垂足为E，交AB于点D，∠A=∠ACD，CE=1，BC=3，则AB的长为（        ）

A．4 B．5 C．5.5 D．6
【答案】B
【解析】
【分析】
根据角平分线的定义得到，根据垂直的定义得到，根据全等三角形的性质得到，，求得，根据等腰三角形的性质得到，于是得到结论．
【详解】
解：平分，
，
，
，
在与中，
，
，
，，
，
，
，
，
故选：B．
【点睛】
本题考查了全等三角形的判定和性质，角平分线的定义，等腰三角形的性质，熟练掌握全等三角形的判定和性质定理是解题的关键．
3．（2022·山东潍坊·八年级期末）如图，在△ABC中，点D，E在边BC上，BD＝CE，则添加下列条件后，仍不能证明△ABD≌△ACE的是（       ）

A．AB＝AC B．∠B＝∠C C．AD＝AE D．∠BAD＝∠CAE
【答案】D
【解析】
【分析】
根据全等三角形的判定定理SAS，ASA，AAS，SSS，对每一个选项进行判断即可．
【详解】
解：A、∵AB=AC，
∴∠B=∠C，
∵在△ABD和△ACE中
，
∴△ABD≌△ACE（SAS），
故A选项不符合题意；
B、∵∠B=∠C，
∴AB=AC，
∵在△ABD和△ACE中
，
∴△ABD≌△ACE（SAS），
故B选项不符合题意；
C、∵AD=AE，
∴∠ADE=∠AED，
∴∠ADB=∠AEC，
∵在△ABD和△ACE中
，
∴△ABD≌△ACE（SAS），
故C选项不符合题意；
D、∠BAD＝∠CAE不能得到△ABD≌△ACE，
故D选项符合题意；
故选 D．
【点睛】
本题考查了全等三角形的判定和等腰三角形的性质，全等三角形的判定定理有SAS，ASA，AAS，SSS，等腰三角形的性质：①等边对等角，②等腰三角形底边上的高，底边上的中线，顶角的平分线三线重合．
4．（2022·河北石家庄·八年级期末）如图，在中，，垂足为D，EF垂直平分AC，交AC于点F，交BC于点E，，若的周长为26cm，，则DC的长为（       ）

A．4 B．8 C．6 D．7
【答案】B
【解析】
【分析】
根据线段垂直平分线和等腰三角形性质得出AB＝AE＝CE，能推出2DE+2EC＝16（cm），即可得出答案．
【详解】
∵AD⊥BC，BD＝DE，EF垂直平分AC，
∴AB＝AE＝EC，
∵△ABC周长26cm，AF＝5cm，
∴AC＝10（cm），
∴AB+BC＝16（cm），
∴AB+BE+EC＝16（cm），
即2DE+2EC＝16（cm），
∴DE+EC＝8（cm），
∴DC＝DE+EC＝8（cm），
故选：B
【点睛】
本题主要考查三角形的线段长度，解题的关键是熟知等腰三角形的性质及垂直平分线的性质．
5．（2022·云南德宏·八年级期末）以下说法中，正确的命题的个数为（       ）
①三角形的中线、高、角平分线都是直线；
②三角形的一个外角等于两个内角的和；
③有两条边和一角对应相等的两个三角形全等；
④三角形具有稳定性；
⑤如果三角形的一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形
A．2 B．3 C．4 D．5
【答案】A
【解析】
【分析】
根据等腰三角形的性质、三角形的全等以及三角形的外角的性质对各选项分析判断即可得解．
【详解】
解：三角形的中线、高、角平分线都是线段，故①选项错误，不符合题意；
三角形的一个外角等于它不相邻的两个内角之和，故②选项错误，不符合题意；
有两边及一角对应相等的两个三角形不一定全等，必须是夹角，故③选项错误，不符合题意；
三角形具有稳定性正确，故④选项正确，符合题意；
如果三角形的一个外角平分线平行三角形的一边，那么这个三角形是等腰三角形正确，故⑤选项正确，符合题意；
故选：A．
【点睛】
本题考查三角形的判定和性质、等腰三角形的判定和性质以及三角形的外角的性质，解题的关键是熟练掌握基本知识，属于中考常考题型．
6．（2022·陕西渭南·一模）如图，在△ABC中，AB＝AC＝4，∠BAC＝120°，AD是△ABC的中线，AE是∠BAD的平分线，过点D作DF∥AB交AE的延长线于点F，则DF的长为_____．

【答案】2
【解析】
【分析】
根据已知条件，△ABC是等腰三角形，D为底边的中点，可得AD⊥BC，∠BAD＝∠CAD，根据AE是∠BAD的角平分线，进而可得∠DAF＝∠F，AD＝DF，根据含30度角的直角三角形的性质求得AD的长，即可求得的长．
【详解】
解：∵△ABC是等腰三角形，D为底边的中点，
∴AD⊥BC，∠BAD＝∠CAD，
∵∠BAC＝120°，
∴∠BAD＝60°，∠ADB＝90°，
∵AE是∠BAD的角平分线，
∴∠DAE＝∠EAB＝30°，
∵DF∥AB，
∴∠F＝∠BAE＝30°，
∴∠DAF＝∠F＝30°，
∴AD＝DF，
∵AB＝6，∠B＝30°，
∴ADAB＝2，
∴DF＝2，
故答案为：2．
【点睛】
本题考查了等腰三角形的性质与判定，含30度角的直角三角形的性质，掌握含30度角的直角三角形的性质是解题的关键．
7．（2022·河北唐山·八年级期末）已知：如图，D为的边BC延长线上一点，和的角平分线交于点O，过点О作BC的平行线，分别交AB，AC于点E，F，若，，则__________．

【答案】2
【解析】
【分析】
根据已知角平分线和平行线可证明等腰三角形，所以根据已知易证△BEO与△CFO是等腰三角形，即可解答．
【详解】
解：∵BO平分∠ABC，
∴∠ABO＝∠OBC，
∵OEBC，
∴∠OBC＝∠EOB，
∴∠ABO＝∠EOB，
∴EB＝EO＝5，
∵CO平分∠ACD，
∴∠ACO＝∠OCD，
∵OEBC，
∴∠EOC＝∠OCD，
∴∠ACO＝∠EOC，
∴FO＝FC＝3，
∴EF＝EO﹣FO＝5﹣3＝2，
故答案为：2．
【点睛】
本题考查了平行线的性质，等腰三角形的判定与性质，熟练掌握已知角平分线和平行线可证明等腰三角形，是解题的关键．
8．（2022·云南曲靖·八年级期末）已知a、b为等腰三角形的两边长，且满足，则等腰三角形的周长是______．
【答案】18或15
【解析】
【分析】
直接利用非负数的性质得出a，b的值，再利用等腰三角形的性质得出答案．
【详解】
解∶∵（a-7）2+|b-4|=0，
∴a-7=0，b-4=0，
解得：a=7，b=4，
∵等腰三角形的两边长分别为a，b，
∴当a为腰长时，
∴等腰三角形的周长为：7+7+4=18，
当b为腰长时，
等腰三角形的周长为：7+4+4=15，
故此等腰三角形的周长为18或15．
故答案为：18或15．
【点睛】
此题主要考查了等腰三角形的性质以及非负数的性质，正确分情况讨论是解题关键．
9．（2022·天津西青·八年级期末）如图，在一个三角形纸片ABC中，，，点D在边BC上，将沿直线AD折叠，点B恰好落在AC边上的点E处．若，则AC的长是______．

【答案】6
【解析】
【分析】
由折叠性质可知，，由，可得是等腰三角形，根据等腰三角形的性质可求的长，进而可求的长．
【详解】
解：由折叠性质可知，
∵
∴是等腰三角形
∵
∴
∴
故答案为：6．
【点睛】
本题考查了折叠的性质，等腰三角形的判定与性质．解题的关键在于熟练掌握等腰三角形的性质．
10．（2022·湖北荆州·八年级期末）如图，△ABC中，BO平分∠ABC，CO平分∠ACB，MN经过点O，与AB，AC相交于点M，N，且MN∥BC，若AB＝5cm，AC＝6cm，则△AMN的周长为_______．

【答案】11cm
【解析】
【分析】
由题意易得，然后由平行线的性质可得，则有，进而可得，最后问题可求解．
【详解】
解：∵BO平分∠ABC，CO平分∠ACB，
∴，
∵MN∥BC，
∴，
∴，
∴，
∵AB＝5cm，AC＝6cm，
∴；
故答案为11cm．
【点睛】
本题主要考查平行线的性质、角平分线的定义及等腰三角形的判定，熟练掌握平行线的性质、角平分线的定义及等腰三角形的判定是解题的关键．
11．（2022·江苏盐城·二模）已知：如图，，，AC和BD相交于点O．点M是BC的中点，连接OM．


(1)求证：；
(2)求的度数．
【答案】(1)见解析
(2)
【解析】
【分析】
（1）根据边边边直接证明两三角形全等即可；
（2）根据全等三角形的性质可得，进而证明是等腰三角形，根据三线合一可得，即可求得．
(1)
证明：在和中，
，
∴（SSS）．
(2)
解：由（1）得：，
∴OB=OC
∴是等腰三角形．
∵点M是BC的中点，
∴，
∴．
【点睛】
本题考查了全等三角形的性质与判定，等腰三角形的性质与判定，掌握以上知识是解题的关键．
12．（2022·广西百色·八年级期末）如图，已知AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，AD与EF相交于点M．

(1)求证：△ADE≌△ADF；
(2)求证：AD垂直平分EF．
【答案】(1)见解析
(2)见解析
【解析】
【分析】
（1）由角平分线的性质定理可得DE＝DF，然后根据“HL”可进行求证；
（2）由（1）可得AE＝AF，然后根据等腰三角形的性质可求证．
(1)
证明：∵AD平分∠BAC，DE⊥AB，DF⊥AC，
∴DE＝DF．
∵DE⊥AB，DF⊥AC，
∴∠AED＝∠AFD＝90°，
∴在Rt△ADE和Rt△ADF中，，
∴Rt△ADE≌Rt△ADF（HL）；
(2)
证明：∵Rt△ADE≌Rt△ADF
∴AE＝AF
又∵AD是△ABC的角平分线
∴AD是线段EF的垂直平分线．
【点睛】
本题主要考查角平分线的性质定理、“HL”及等腰三角形的性质，熟练掌握角平分线的性质定理、“HL”及等腰三角形的性质是解题的关键．
13．（2022·湖南岳阳·八年级期末）已知：如图所示，Rt△ABC中，，，O为BC的中点．


(1)写出点O到△ABC的三个顶点A、B、C的距离的关系（不要求证明）
(2)如果点M、N分别在线段AC、AB上移动，且在移动中保持．试判断△OMN的形状，并证明你的结论．
(3)如果点M、N分别在线段CA、AB的延长线上移动，且在移动中保持，试判断（2）中结论是否依然成立，如果是请给出证明．
【答案】(1)
(2)△OMN是等腰直角三角形；见解析
(3)成立；见解析
【解析】
【分析】
（1）根据直角三角形斜边中线的性质即可解答；
（2）连接OA，证明，利用全等三角形的性质推出，通过角度等量代换推出即可解答；
（3）连接OA，与（2）同理，证明，利用全等三角形的性质、等腰直角三角形的性质可以解答．
(1)
解：如图1，连接OA，


Rt△ABC中， ，O为BC的中点，
AO为Rt△ABC斜边的中线，
，
；
(2)
△OMN是等腰直角三角形，证明如下：
Rt△ABC中，，，，
，，
，，
，
在和中，
，
，
，，
，
，
△OMN是等腰直角三角形；
(3)
结论成立，证明如下：
如图2，连接OA，


，，
，，
，
，，
，
在和中，
，
，
，，
，
，
△OMN是等腰直角三角形；
【点睛】
本题考查直角三角形斜边中线的性质、全等三角形的判定与性质、等腰三角形的性质、等腰直角三角形的性质等，根据题意综合运用上述知识是解题的关键．
14．（2022·浙江温州·模拟预测）如图，在 6×4 的方格纸 ABCD 中，请按要求画格点三角形（端点在格点上），且三角形的各个顶点均不与点 A，B，C，D 重合，各边不落在格线上．

(1)在图 1 中画格点△EFG，使三角形的各顶点落在四边形 ABCD 的边上，且使它为等腰三角形．
(2)在图 2 中画格点△EFG 和△MNH，且使得它们全等，每条对应边都相互垂直．
【答案】(1)见解析（答案不唯一，只要符合要求即可）
(2)见解析（答案不唯一，只要符合题目要求即可）
【解析】
【分析】
（1）根据题目要求画△EFG即可；
（2）根据题意要求画出两个格点三角形即可．
(1)
这样的等腰三角形的顶点一定在四边形某条边的中点上，如图所示：


(2)
根据题意可以画出如图所示的图形：


【点睛】
本题主要考查了作图——应用于设计作图，解题的关键是理解题意，学会利用数形结合的思想解决问题．
15．（2022·海南华侨中学八年级期末）如图，在中，，，AD是BC的中线，．


(1)求证：
(2)是什么形状的三角形？请说明理由．
【答案】(1)见解析
(2)为等腰直角三角形，理由见解析
【解析】
【分析】
（1）根据条件证明即可得到结论；
（2）由得到边、角之间的关系，即可证得为等腰直角三角形．
(1)
∵中，，，
∴ ， ，
∴，
∴，
在和中，

∴
∴
(2)
为等腰直角三角形．理由如下
由（1）得
∴，，
∵，
∴．
∴为等腰直角三角形．
【点睛】
本题主要考查了全等三角形的判定和性质，等腰三角形的判定、中线的性质，掌握并能综合运用上述知识点是解题的关键．




【培优检测】
1．（2022·广东深圳·二模）如图，在中，按以下步骤作图：①分别以点，为圆心，大于长为半径作弧，两弧交于，两点；②作直线交于点，连接．若，，则的度数为（       ）

A．72 B．68 C．75 D．80
【答案】A
【解析】
【分析】
由作图法可得MN是AB的垂直平分线；利用等腰三角形等边对等角的性质，可得∠A=∠DBA=36°，进而求得∠BDC，最后由三角形内角和为180°便可解答．
【详解】
解：由作法得垂直平分，
∴，
∴，
∴，
∵，
∴，
故选：A．
【点睛】
本题考查了垂直平分线的作法和性质，等腰三角形的性质，外角的性质，三角形的内角和定理；解题的关键是掌握等腰三角形的性质．
2．（2022·湖南长沙·八年级期末）如图，中，，于点D，于点E，于点F，，则BF的长为（       ）

A．5 B．6 C．7 D．8
【答案】D
【解析】
【分析】
过点D作DH⊥AC于点H，由题意易得AD平分∠CAB，则有DE=DH，然后根据等积法可进行求解．
【详解】
解：过点D作DH⊥AC于点H，如图所示：

∵AB＝AC，AD⊥BC，
∴AD平分∠CAB，
∵DE⊥AB，DE＝4，
∴DE=DH=4，
∵，
∴，
∴；
故选D．
【点睛】
本题主要考查等腰三角形的性质及角平分线的性质定理，熟练掌握等腰三角形的性质及角平分线的性质定理是解题的关键．
3．（2022·山东济宁·八年级期末）在△ABC中，已知AB=AC，∠A=36°，AB的垂直平分线MN交AC于D．下列结论中：①∠C=72°；②BD是△ABC的中线；③∠BDC=100°；④△ABD是等腰三角形；⑤AD=BD=BC．正确的序号有（        ）
A．①③④ B．①④⑤ C．①②⑤ D．②④⑤
【答案】B
【解析】
【分析】
根据题意画出图形，再根据在中，已知，求出的度数；由线段垂直平分线的性质求出的度数，故可得出的度数，进而得出是的平分线；由三角形内角和定理可求出的度数；由线段垂直平分线的性质，易证得是等腰三角形．
【详解】
解：中，，，
，
故①正确；
是的垂直平分线，
，
，
，
是的平分线，
故②错误；
在中，，，
．
故③错误；
是的垂直平分线，

是等腰三角形；
故④正确；
是线段的垂直平分线，
，
，
，
，
，故⑤正确，
故正确的有：①④⑤．
故选：B．
【点睛】
本题考查的是线段垂直平分线的性质及等腰三角形的判定与性质，解题的关键是熟知垂直平分线上任意一点，到线段两端点的距离相等．
4．（2022年浙江省温州市中学自主招生模拟数学试题）如图，将△ABC沿DE折叠，使点A与BC边的中点F重合，下列结论中：①EF∥AB且2EF＝AB；②∠BAF＝∠CAF；③S四边形ADEF＝AF·DE；④∠BDF＋∠FEC＝2∠BAC，正确的个数是（       ）

A．1 B．2 C．3 D．4
【答案】B
【解析】
【分析】
根据翻折变换的性质可得AD＝DF，AE＝EF，进而得出AF⊥DE，∠BAF＝∠DFA，∠CAF＝∠AFE，根据平行线的判定和等腰三角形三线合一的性质判断只有AB＝AC时①②正确；根据S四边形ADFE＝S△ADF＋S△AEF判断出③正确；根据翻折的性质和平角的定义表示出∠ADE和∠AED，然后利用三角形的内角和定理列式整理即可得到∠BDF＋∠FEC＝2∠BAC，判断出④正确．
【详解】
解：∵△ABC沿DE折叠，点A与BC边的中点F重合，
∴AD＝DF，AE＝EF，
∴AF⊥DE，∠BAF＝∠DFA，∠CAF＝∠AFE，
只有AB＝AC时，∠BAF＝∠CAF＝∠AFE，此时EF∥AB，2EF＝AB，
故①②错误；
如图，∵AF⊥DE，
∴S四边形ADFE＝S△ADF＋S△AEF＝AF•DO＋AF•OE＝AF•（DO＋OE）＝AF•DE，
故③正确；
由翻折的性质得，∠ADE＝（180°−∠BDF），∠AED＝（180°−∠FEC），
在△ADE中，∠ADE＋∠AED＋∠BAC＝180°，
∴（180°−∠BDF）＋（180°−∠FEC）＋∠BAC＝180°，
整理得，∠BDF＋∠FEC＝2∠BAC，故④正确．
综上所述，正确的是③④，共2个．
故选：B．

【点睛】
本题考查了翻折变换的性质，平行线的判定，等腰三角形三线合一的性质，三角形的内角和定理，熟记各性质并准确识图是解题的关键．
5．（2022·山东临沂·八年级期末）如图，在四边形ABCD中，AC平分∠BAD，AD=AC，在AC上截取AE=AB，连接DE，BE，并延长BE交CD于点F，以下结论：①△BAC≌△EAD；②∠CBE=∠CDE；③CF=EF；其中正确的有（        ）个．

A．0 B．1 C．2 D．3
【答案】D
【解析】
【分析】
根据角平分线的定义得出，根据等腰三角形的性质得出，，根据三角形内角和定理得出，，求出，根据全等三角形的判定定理即可判断①，求出，即可判断③，求出，，求出，即可判断②．
【详解】
解：平分，
，
，，
，，
，，
，
在和中，
，
，故①正确；
，
，，
，
，故③正确；
，，，
，
，
，故②正确；
即正确的个数是3，
故选：D．
【点睛】
本题考查了等腰三角形的性质，三角形内角和定理，三角形外角性质，全等三角形的判定定理和性质定理等知识点，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理有，，，，两直角三角形全等还有等．
6．（2022·黑龙江牡丹江·八年级期末）在△ABC中，AB=AC，AB的垂直平分线交AB于点D，交直线AC于点E，∠AEB=80°，那么∠BAC等于________．
【答案】50° 或130°
【解析】
【分析】
分两种情况：∠BAC为锐角，∠BAC为钝角，根据线段垂直平分线的性质可求出AE=BE，然后根据三角形内角和定理即可解答．
【详解】
解：如图1，∵DE 垂直平分AB，

∴AE=BE，
∴∠BAC=∠ABE，
∵∠AEB=80°，
∴∠BAC=∠ABE==50°；
如图2，∵DE 垂直平分AB，

∴AE=BE，
∴∠BAE=∠ABE，
∵∠AEB=80°，
∴∠BAE=∠EBA==50°，
∴∠BAC=180°-50°=130°；
故答案为：50°或130°．
【点睛】
此题主要考查线段的垂直平分线及等腰三角形的判定和性质．线段的垂直平分线上的点到线段的两个端点的距离相等．
7．（2022·山东·武城县教育教学研究中心一模）如图，在四边形ABCD中，，，其中，那么______．

【答案】75°##75度
【解析】
【分析】
由等腰三角形的性质，设，则，结合题意及三角形内角和180°列方程，解方程即可．
【详解】
解：





设，则
由题意得









故答案为：75°．

【点睛】
本题考查等腰三角形的性质、三角形的内角和等知识，是基础考点，掌握相关知识是解题关键．
8．（2022·陕西延安·八年级期末）如图，在中，直线垂直平分BC交AC于点Q，BP平分交直线于点P.若，，则___________.

【答案】34°##34度
【解析】
【分析】
先证明∠ABP=∠PBC，∠ABP=∠PCB，再由三角形内角和定理求出∠ABP=32°，据此求解即可．
【详解】
解：∵直线l是线段BC的垂直平分线，
∴PB=PC，
∴∠PBC=∠PCB，∠BPD=∠CPD
∵BP平分∠ABC，
∴∠ABP=∠PBC，
∴∠ABP=∠PCB，
∵∠A+∠ACB+∠ABC=180°，∠BAC=60°，∠ACP=24°，
∴3∠ABP+60°+24°=180°，
∴∠ABP=32°，
∴∠PBC=∠PCB=32°，
∴，
故答案为：34°．

【点睛】
本题主要考查了线段垂直平分线的性质，等腰三角形的性质与判定，三角形内角和定理，三角形外角的性质，熟知线段垂直平分线的性质是解题的关键．
9．（2022·安徽宿州·八年级期中）如图，，点A是BO延长线上的一点，OA＝10cm，动点P从点A出发沿AB以2cm/s的速度移动，动点Q从点O出发沿OC以1cm/s的速度移动，如果点P，Q同时出发，用t（s）表示移动的时间，当t＝________时，△POQ是等腰三角形．

【答案】或10s
【解析】
【分析】
根据是等腰三角形，分两种情况进行讨论：点在上，或点在上．
【详解】
解：当时，是等腰三角形；
如图1所示：
，
当时，

解得；
当时，是等腰三角形；
如图2所示：
，；
当时，；
解得；
故答案为：或10s．


【点睛】
本题主要考查了等腰三角形的性质，解题的关键是掌握等腰三角形的性质得出方程进行求解，注意分类讨论．
10．（2022·青海·西宁市教育科学研究院八年级期末）如图，在△ABC中，∠ABC＝90°，AB＝BC＝8cm，BD是△ABC的高，动点P在线段AB上由A向B运动，速度为1cm/s；动点Q在线段BC上由B向C运动，速度为2cm/s．动点P，Q同时出发，当一个点停止运动时，另一个点也随之停止．连接AQ，交BD于点E．设点P的运动时间为t秒，当∠BPE＝∠BQE时，______秒．

【答案】
【解析】
【分析】
∠BPE和∠BQE相等，加上BE为公共边，∠PBE=∠QBE，即有三角形全等，利用对应边相等列方程即求出t的值．
【详解】
∵BD平分∠ABC
∴∠PBE=∠QBE
在△BPE与△BQE中

∴△BPE≌△BQE（AAS）
∴BP=BQ
∵BP=AB-AP=8-t
∴8-t=2t
解得：t=，
∴t=时，∠BPE和∠BQE相等
【点睛】
本题考查了等腰直角三角形，全等三角形的判定和性质．解决本题的关键是熟练掌握等腰三角形三线合一性质．
11．（2022·广东中山·三模）新定义：顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”．

(1)如图1，和互为“兄弟三角形”，点A为重合的顶角顶点．求证：．
(2)如图2，和互为“兄弟三角形”，点A为重合的顶角顶点，点D、E均在外，连接BD、CE交于点M，连接AM，求证：AM平分．
【答案】(1)证明过程见解析
(2)证明过程见解析
【解析】
【分析】
（1）根据“兄弟三角形”的定义得到∠BAC=∠DAE，进而得到∠CAE=∠BAD，再证明即可得到答案；
（2）过点A作AG⊥DM于G，AH⊥EM于H，证明△BAD≌△CAE，根据全等三角形的对应高相等得到AG=AH，根据角平分线的判定定理证明结论．
(1)
证明：∵和互为“兄弟三角形”，
∴，，，
∴，
即，
∴（SAS），
∴．
(2)
证明：如图，过点A作于G，于H，

∵和互为“兄弟三角形”，
∴，，，
∴，
即，
∴（SAS），
∴，
∵，，
∴，
∴（SAS），
∴，
∴AM平分．
【点睛】
本题考查的是“兄弟三角形”的定义、全等三角形的判定和性质、等边三角形的判定和性质，正确理解“兄弟三角形”的定义是解题的关键．
12．（2021·湖南·常德市第七中学八年级期中）如图，中，，EF垂直平分，交于点，交于点，且．

(1)若，求的度数；
(2)若周长，，求长．
【答案】(1)35°
(2)8cm
【解析】
【分析】
（1）根据等腰三角形性质和线段垂直平分线的性质易得AB=AE=CE，∠C=∠EAC，由三角形内角和定理可知∠B=∠AEB的度数，最后结合三角形的外角性质求得答案；
（2）根据已知能推出2DE+2EC=16cm，即可得出答案．
(1)
解：∵，
∴
又∵垂直平分
∴
∴．
(2)
解：∵，
∴
又∵垂直平分
∴
∴
∵cm，且cm
∴cm
∴AB+BE+CE=16cm
∴cm
∴cm
∴＝cm．
【点睛】
本题主要考查了等腰三角形的性质、线段垂直平分线的性质、三角形内角和定理、三角形外角性质等，掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键．
13．（2022·广东深圳·二模）如图，已知射线BC⊥AB，以AB为斜边作Rt△ABD，延长AD到E，使得AD＝DE，连接BE，BF平分∠CBE交AE于点F．

(1)求证：BD＝DF；
(2)若AB＝2，以AE为边向下作∠AEG＝45°，交射线BC于点G，求BG的长．
【答案】(1)见解析
(2)2
【解析】
【分析】
(1)首先可证得BD垂直平分AE，可得AB=BE，，可得，再根据BF平分∠CBE，可得，据此即可求得，即可证得结论；
(2)首先可证得，进而证得，，再根据，即可求得BG的长．
(1)
证明：

的斜边是


又
垂直平分AE





平分














(2)
解：如图：延长BF交EG于点H

，


，





【点睛】
本题考查了线段垂直平分线的判定与性质，等腰三角形的性质，三角形内角和定理及外角的性质，角平分线的定义，作出辅助线是解决本题的关键．
14．（2022·湖南·常德市第七中学八年级期末）已知：在△ABC中，∠B=60°，D、E分别为AB、BC上的点，且AE、CD交于点F．

(1)如图1，若AE、CD为△ABC的角平分线．
①求∠AFC的度数；
②若AD=5，CE=3，求AC的长
(2)如图2，若∠FAC=∠FCA=30°，求证：AD=CE
【答案】(1)①120；②8
(2)见解析
【解析】
【分析】
（1）①根据角平分线的性质可得根据已知条件与三角形内角和定理，可得，进而可得；
②在AC上截取AG=AD，连接FG，证明，，根据即可求解；
（2）在AE上截取FH=FD，连接 CH，证明，进而证明，即可得证
(1)
①分别平分，
                              
又，故，


②在AC上截取AG=AD，连接FG，

,
        

               
又



(2)
在AE上截取FH=FD,连接 CH，

∵∠FAC=∠FCA=30°
∴FA=FC
在
，
∴
∴AD=CH，∠DAF=∠HCF
∴∠CEH=∠B+∠DAF=60°+∠DAF，
∠CHE= ∠HAC+∠HCA=60°+∠HCF
∴∠CEH=∠CHE
∴CH=CE
∴AD=CE.
【点睛】
本题考查了角平分线定义，三角形内角和定理的应用，全等三角形的性质与判定，掌握全等三角形的性质与判定是解题的关键．
15．（2022·河南平顶山·八年级期中）
(1)阅读理解：我们知道，只用直尺和圆规不能解决的三个经典的希腊问题之一是三等分任意角，但是这个任务可以借助如图所示的一边上有刻度的勾尺完成，勾尺的直角顶点为，“宽臂”的宽度，（这个条件很重要哦！）勾尺的一边满足，，三点在同一直线上且．
如图所示，下面以三等分为例说明利用勾尺三等分锐角的过程：
第一步：画直线使，且这两条平行线之间的距离等于（说明：两条平行线中的一条直线上任意一点，到另一条直线的距离，就是这两条平行线之间的距离）；
第二步：移动勾尺到合适位置，使其顶点落在上，使勾尺的边经过点，同时让点落在的边上；
第三步：标记此时点和点所在位置，作射线和射线．
请完成第三步操作，图中的三等分线是射线________、________．

(2)在（1）的图中，过点做于点，根据（1）中第一步的操作可知，请你证明．
【答案】（1）；；（2）见解析
【解析】
【分析】
（1）作射线BQ和射线BP，射线BQ和射线BP就是∠ABC的三等分线；
（2）根据线段的垂直平分线的性质定理，等腰三角形的三线合一，角平分线的判定定理，即可证明．
(1)
解：作射线BQ和射线BP，如图所示：


射线BQ和射线BP就是∠ABC的三等分线．

故答案为：BQ；BP．
(2)
∵，，
∴，
∵，，
∴，
∴，
∴．
【点睛】
本题考查三角形综合题，垂直平分线性质定理，角平分线的判定定理，等腰三角形的判定和性质，解题的关键是理解题意，灵活运用所学知识解决问题，学会利用轴对称构造角相等，属于中考常考题型．