数学七年级上册4.2 直线、射线、线段教学ppt课件

这是一份数学七年级上册4.2 直线、射线、线段教学ppt课件，共31页。PPT课件主要包含了1AB＜AC，则线段AB＝2a，两点间的线段，两点之间线段最短等内容，欢迎下载使用。
1.会用尺规画一条线段等于已知线段，会比较两条线段的长短. (重点)2.理解线段等分点的意义.3.能够运用线段的和、差、倍、分关系求线段的长度. (重点、难点)4.体会文字语言、符号语言和图形语言的相互转化.5.了解两点间距离的意义，理解“两点之间，线段最短”的线段性质，并学会运用. (难点)
问题:老师手里的纸上有一条线段，你能在你的本上作出一条同样大小的线段来吗？
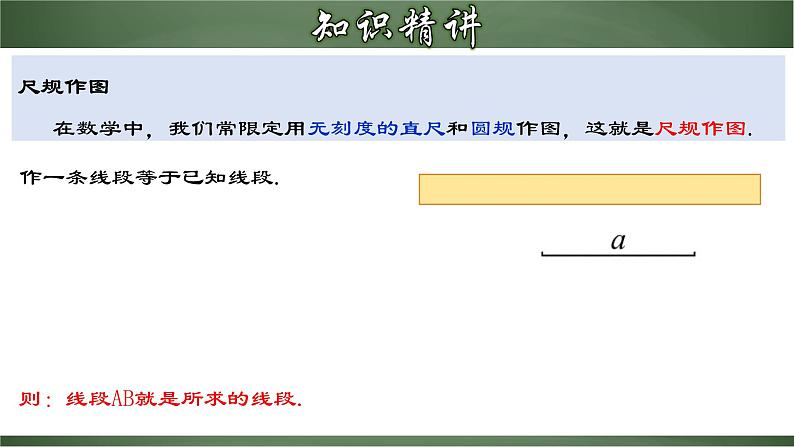
尺规作图 在数学中，我们常限定用无刻度的直尺和圆规作图，这就是尺规作图.  
作一条线段等于已知线段.
则：线段AB就是所求的线段.
如何比较两个人的身高？
怎样比较两条线段的长短呢？你能从比身高上受到一些启发吗？
判断线段AB和CD的大小.(1)如图1，线段AB和CD的大小关系是AB___CD；(2)如图2，线段AB和CD的大小关系是AB___CD；(3)如图3，线段AB和CD的大小关系是AB___CD.
如图，线段AB和AC的大小关系是怎样的？线段AC与线段AB的差是哪条线段？你还能从图中观察出其他线段间的和、差关系吗？
(2) AC－AB＝BC， AC－BC＝AB， BC＋AB＝AC.
如图，已知线段a和线段b，怎样通过作图得到a与b的和、a与b的差呢？
如图，已知线段a、b，作一条线段，使它等于2a－b.
则：线段AC=2a－b.
如图，已知线段a，求作线段AB＝2a.
如上图，点M把线段AB分成相等的两条线段AM和BM；点M叫做线段AB的中点.
类似地，还有线段的三等分点、四等分点等.
如图，从A地到B地有四条道路，除它们之外能否再修一条从A地到B地的最短道路？如果能，请联系你以前所学的知识，在图上画出最短路线.
估计下列图中线段AB与线段AC的大小关系，再用刻度尺或用圆规来检验你的估计.
AB___AC AB___AC AB___AC
例1.若AB=6cm，点C是线段AB的中点，点D是线段CB的中点，求：线段AD的长是多少?
例2.如图，B、C是线段AD上两点，且AB：BC：CD=3：2：5，E、F分别是AB、CD的中点，且EF=24，求线段AB、BC、CD的长．
解析：根据已知条件AB：BC：CD=3：2：5，不妨设AB=3x,BC =2x,CD=5x,然后运用线段的和差倍分，用含x的代数式表示EF的长，从而得到一个关于x的一元一次方程，解方程，得到x的值，即可得到所求各线段的长.
解：设AB=3x，BC=2x，CD=5x，
因为E、F分别是AB、CD的中点，
因为EF=24，所以6x=24,解得x=4.
所以AB=3x=12，BC=2x=8，CD=5x=20.
【点睛】求线段的长度时，当题目中涉及到线段长度的比例或倍分关系时，通常可以设未知数，运用方程思想求解.
解析：根据已知条件，不妨设BD=xcm，则AB=3xcm,CD=4xcm,易得AC=6xcm.在由线段中点的定义及线段的和差关系，用含x的代数式表示EF的长，从而得到一个一元一次方程，求解即可.
解：设BD=xcm,则AB=3xcm，CD=4xcm，AC =6xcm，
所以AB=3xcm=12cm，CD=4xcm=16cm.
例3.A，B，C三点在同一直线上，线段AB=5cm，BC=4cm，那么A，C两点的距离是（　　）A．1cm B．9cm C．1cm或9cm D．以上答案都不对
解析：分以下两种情况进行讨论：当点C在AB之间上，故AC=AB-BC=1cm；当点C在AB的延长线上时，AC=AB+BC=9cm．
【点睛】无图时求线段的长，应注意分类讨论，一般分以下两种情况：点在某一线段上；点在该线段的延长线.
已知A，B，C三点共线，线段AB=25cm，BC=16cm，点E，F分别是线段AB，BC的中点，则线段EF的长为（　　）A．21cm或4cm B．20.5cm C．4.5cm D．20.5cm或4.5cm
1.连接_____________的______叫做两点的距离.2.两地间一段弯曲的公路改为直路，可以缩短路程，其理由是_____________________.3.如图,以C为端点的线段有________________________.4.如图,A、B、C、D四点在同一直线上，若AB=CD， 则AC___BD.(填“>、