数学北师大版6 实数教学ppt课件

这是一份数学北师大版6 实数教学ppt课件，共22页。PPT课件主要包含了学习目标及重难点，课程导入，课程讲授，探索1实数的分类，有理数集合，无理数集合，有理数，无理数，负整数，正分数等内容，欢迎下载使用。
1.了解实数的概念和意义，能按要求对实数进行分类；（重点）2.了解实数和数轴上的点一一对应，能找出实数在数轴上的对应位置.（难点）
(1)什么是有理数？有理数怎么分类？(2)什么是无理数？无理数的常见形式有哪些？
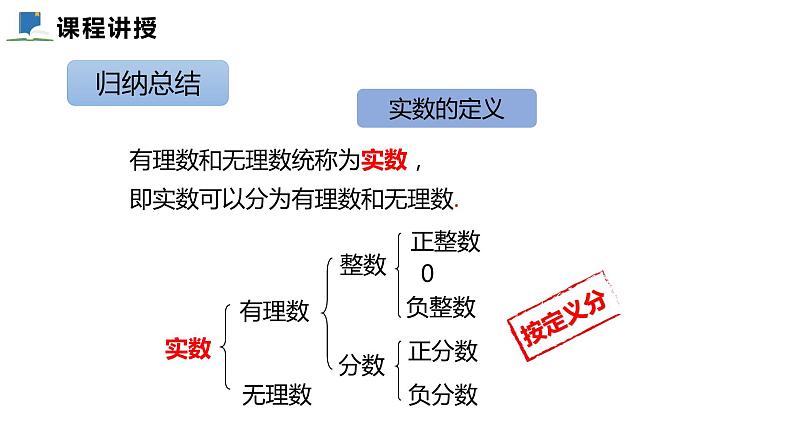
整数和分数统称为有理数.
有理数分为正有理数、0、负有理数.
无限不循环小数称为无理数.
无理数的常见形式:①一般的无限不循环小数，看似循环而实质不循环的小数；②圆周率π以及含π的数；③开方开不尽的数.
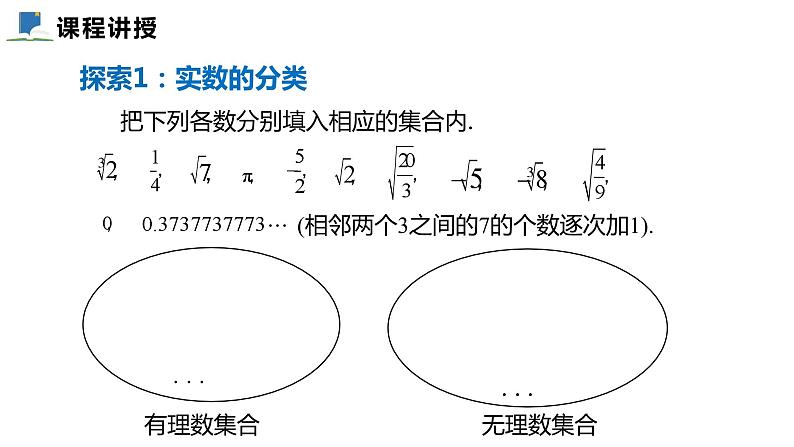
你会对已有的有理数与无理数进行归类吗？
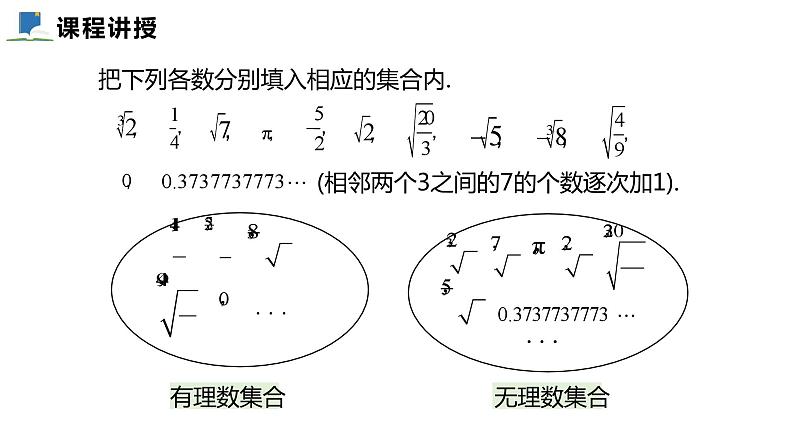
把下列各数分别填入相应的集合内.
(2) ， 是无限不循环小数， 所以这两个数也是无理数.
有理数和无理数统称为实数，即实数可以分为有理数和无理数.
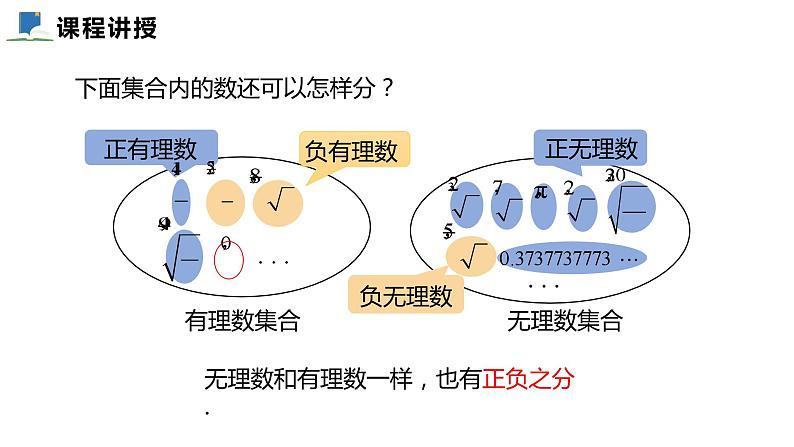
无理数和有理数一样，也有正负之分.
下面集合内的数还可以怎样分？
实数又可以分为正实数、0和负实数.
有理数范围内的一些概念是否适用于实数？
在实数范围内，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.
a是一个实数，它的相反数为____.
a是一个实数,它的绝对值为
当a≠0时，那么它的倒数为____.
与______互为相反数
(1)分别写出 的相反数； (2)求 的倒数； (3)求 的绝对值．
解：(1)若a是一个实数,它的相反数为-a； ∴ 的相反数是 ；π-3.14的相反数是3.14-π.
(2)当a≠0时，它的倒数为 ； ∴ 的倒数是 ； 的倒数是 .
(3)若a是一个小于0的实数，则其绝对值为-a， ∴ 的绝对值是4 .
实数和有理数一样，可以进行加、减、乘、除、乘方运算，而且有理数的运算法则与运算律对实数仍然适用.
观察下列式子，你发现了什么？
(1) 如下图，OA=OB，数轴上点A对应的数是什么？它介于哪两个整数之间？
解：根据勾股定理，可得OB2=12+12=2，∴OB= . 又∵OA=OB， OA= ，∴数轴上点A对应的数是 .∵ ≈1.414，∴点A介于整数1和2之间.
(2) 你能在数轴上找到 对应的点吗？与同伴进行交流.
解：在数轴上数2的对应点处作长度为1的垂线段AB,
连接原点与点B，以原点O为圆心，OB长为半径画弧交数轴于点2右侧一点C，则点C即为 的对应点.
每一个实数都可以用数轴上的一个点来表示.
反过来，数轴上的每一个点都表示一个实数.
在数轴上，右边的点表示的数比左边的点表示的数大.
实数与数轴上的点的关系
求下列各数的相反数、倒数和绝对值.
求相反数：若a是一个实数,它的相反数为 ； 求倒数：当a≠0时，那么它的倒数为 ；求绝对值：若a是一个实数，则
(3) 的相反数是 -7，倒数是 ，绝对值是7.
解： (1) 的相反数是 ，倒数是 ，绝对值是 .
(2) 的相反数是2，倒数是 ，绝对值是2.
判断下列说法是否正确：(1)带根号的数都是无理数；
分析：带根号的数有可能是能开方开得尽的数，所以这句话错误.
分析：所有实数的绝对值都是正数或0，而所有的正数都比0大，所以这句话正确.
分析：数轴上的每一个点都表示一个实数，实数还包括无理数，所以这句话错误.
(3)数轴上的每一个点都表示一个有理数.
(2)绝对值最小的实数是0；
解：在数轴上数3的对应点处作长度为1的垂线段AB，连接原点O与点B，以原点O为圆心，OB长为半径画弧交数轴于点3右侧一点C，则点C即为 的对应点.
在数轴上找到 对应的点.