人教版八年级上册12.1 全等三角形随堂练习题

这是一份人教版八年级上册12.1 全等三角形随堂练习题，文件包含八年级数学上册全等三角形综合训练五原卷版docx、八年级数学上册全等三角形综合训练五解析版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
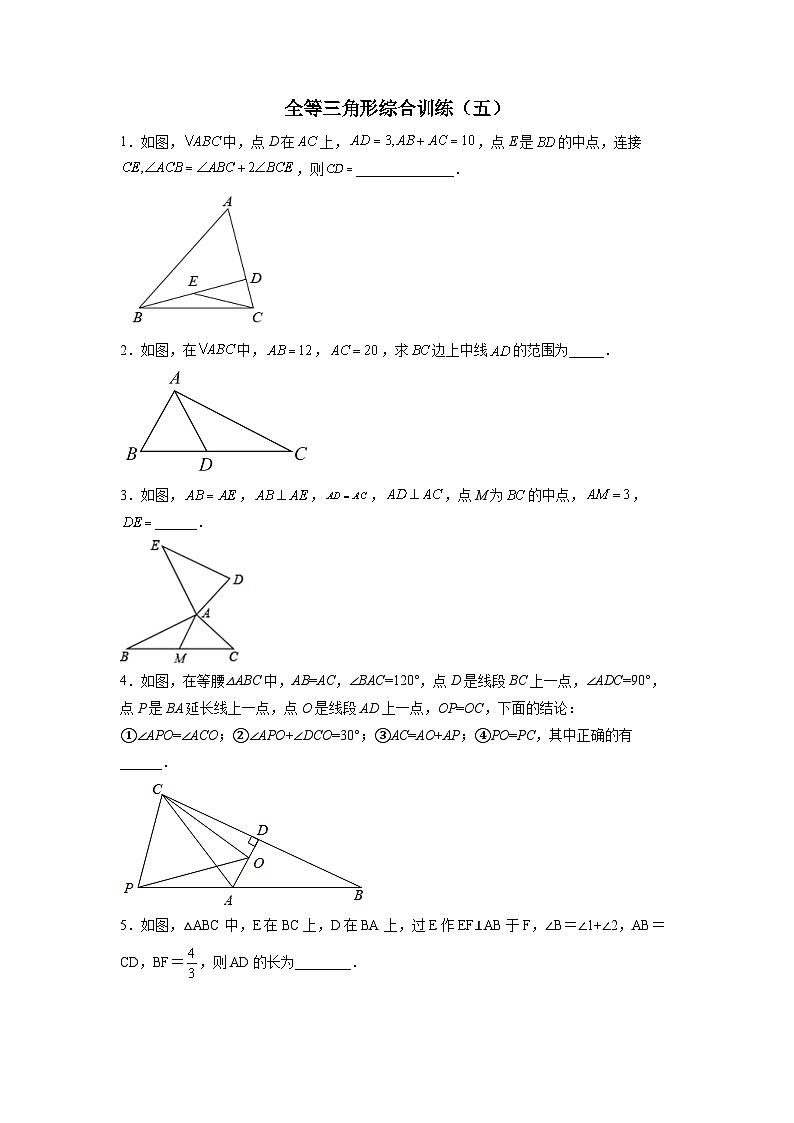
全等三角形综合训练（五）1．如图，中，点D在上，，点E是的中点，连接，则______________．【答案】【详解】解：如图，延长至F，使得，交于点G，∵点E是的中点，∴，在与中，，∴，∴，∵，∴，∵，∴，∴，∴，  设，∵，∴，解得，即．故答案为：2．如图，在中，，，求边上中线的范围为_____．【答案】【详解】解：延长到E，使得，连接，如图，在和中，，∴，∴．∵，∴，∴．故答案为：．3．如图，，，，，点M为的中点，，______．【答案】6【详解】证明：延长AM至N，使，连接，∵点M为的中点，∴，在和中，，∴，∴，，∴，∵，，∴，∴，∴，在和中，，∴，∴．故答案为：6．4．如图，在等腰△ABC中，AB=AC，∠BAC=120°，点D是线段BC上一点，∠ADC=90°，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，下面的结论：①∠APO=∠ACO；②∠APO+∠DCO=30°；③AC=AO+AP；④PO=PC，其中正确的有______．【答案】①②③④【详解】解：连接BO，如图1所示：∵AB=AC，AD⊥BC，∴BO=CO，∴∠OBC=∠OCB，又∵OP=OC，∴OP=OB，∴∠OBP=∠OPB，又∵在等腰△ABC中∠BAC=120°，∴∠ABC=∠ACB=30°，∴∠OBC+∠OBP=∠OCB+∠ACO，∴∠OBP=∠ACO，∴∠APO=∠ACO，故①正确；又∵∠ABC=∠PBO+∠CBO=30°，∴∠APO+∠DCO=30°，故②正确；∵∠PBC+∠BPC+∠BCP=180°，∠PBC=30°，∴∠BPC+∠BCP=150°，又∵∠BPC=∠APO+∠CPO，∠BCP=∠BCO+∠PCO，∠APO+∠DCO=30°，∴∠OPC+∠OCP=120°，又∵∠POC+∠OPC+∠OCP=180°，∴∠POC=60°，又∵OP=OC，∴△OPC是等边三角形，∴PC=PO，∠PCO=60°，故④正确；在线段AC上截取AE=AP，连接PE，如图2所示：∵∠BAC+∠CAP=180°，∠BAC=120°，∴∠CAP=60°，∴△APE是等边三角形，∴AP=EP，又∵△OPC是等边三角形，∴OP=CP，又∵∠APE=∠APO+∠OPE=60°，∠CPO=∠CPE+∠OPE=60°，∴∠APO=∠EPC，在△APO和△EPC中，，∴△APO≌△EPC（SAS），∴AO=EC，又∵AC=AE+EC，AE=AP，∴AO+AP=AC，故③正确；故答案为：①②③④．5．如图，△ABC中，E在BC上，D在BA上，过E作EF⊥AB于F，∠B＝∠1+∠2，AB＝CD，BF＝，则AD的长为________．【答案】【详解】在FA上取一点T，使得FT=BF，连接ET，在CB上取一点K，使得CK=ET，连接DK．∵EB=ET，∴∠B=∠ETB，∵∠ETB=∠1+∠AET，∠B=∠1+∠2，∴∠AET=∠2，∵AE=CD，ET=CK，∴△AET≌△DCK(SAS)，∴DK=AT，∠ATE=∠DKC，∴∠ETB=∠DKB，∴∠B=∠DKB，∴DB=DK，∴BD=AT，∴AD=BT，∵BT=2BF=，∴AD=，故答案为：．6．在中，，，，点是内一点，则点到三个顶点的距离和的最小值是_______．【答案】【详解】如图：以为边作等边三角形，以为边作等边，连接，作，作，交的延长线于．和是等边三角形，，在和中，，，，，当、、、四点共线时，值最小，，，．，，，最小值为．故答案为：．7．如图，△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P，若∠BPC＝50，∠CAP＝______．【答案】40°【详解】解：过点P作PF⊥AB于F，PM⊥AC于M，PN⊥CD于N，如图：设∠PCD=x，∵CP平分∠ACD，∴∠ACP=∠PCD=x，PM=PN，∴∠ACD=2x，∵BP平分∠ABC，∴∠ABP=∠PBC，PF=PM=PN，∵∠BPC＝50°，∴∠ABP=∠PBC=，∴,∴，∴，在Rt△APF和Rt△APM中，∵PF=PM，AP为公共边，∴Rt△APF≌Rt△APM（HL），∴∠FAP=∠CAP，∴；故答案为：40°；8．如图，平行四边形中，于，点为边中点，，，则_________【答案】【详解】解：延长、交于点，连接FC，∵平行四边形中，∴，,,∴，，,又∵点为边中点，得,∴≌(ASA)，，∴，∴，∴,∴,∵,,,,∴,∴,∴,∴,故答案为：.9．已知，如图1，四边形是正方形，，分别在边、上，且，我们把这种模型称为“半角模型”，在解决“半角模型”问题时，旋转是一种常用的方法．(1)在图1中，连接，为了证明结论“ ”，小亮将绕点顺时针旋转后解答了这个问题，请按小亮的思路写出证明过程；(2)如图2，当绕点旋转到图2位置时，试探究与、之间有怎样的数量关系？【答案】(1)见解析；(2)．【详解】（1）证明：如图1，由旋转可得 , , 四边形 为正方形 、 、 三点在一条直线上 在 和 中 （2）结论： ．理由：如图2，把 绕点 逆时针旋转 ，使 与 重合，点 与点 对应，同（1）可证得 ,且 10．已知为等腰三角形，，直线过点（不经过点），过点作于点，过点作于点．(1)如图1，当点位于直线的同侧时，判断与的大小关系，并说明理由；(2)如图2，若点位于直线的两侧，①（1）的结论是否还能成立，请说明理由；②设与交于点，当时，判断与是否相等，并说明理由．【答案】(1)；理由见解析(2)①成立，理由见解析；②，理由见解析【详解】（1）解：，理由如下：∵为等腰三角形，∴，∵，，∴，∵，∴，∴，在和中，，∴，∴；（2）（2）①成立，同理可得，∴；②，理由如下：∵，，∴，∵，，∴，∴，即，∵，∴，∵，∴，∴．11．课堂上，老师提出了这样一个问题：如图1，在中，平分交于点D，且，求证：，小明的方法是：如图2，在上截取，使，连接，构造全等三角形来证明．(1)小天提出，如果把小明的方法叫做“截长法”，那么还可以用“补短法”通过延长线段构造全等三角形进行证明．辅助线的画法是：延长至F，使=______，连接请补全小天提出的辅助线的画法，并在图1中画出相应的辅助线；(2)小芸通过探究，将老师所给的问题做了进一步的拓展，给同学们提出了如下的问题：如图3，点D在的内部，分别平分，且．求证：．请你解答小芸提出的这个问题（书写证明过程）；(3)小东将老师所给问题中的一个条件和结论进行交换，得到的命题如下：如果在中，，点D在边上，，那么平分小东判断这个命题也是真命题，老师说小东的判断是正确的．请你利用图4对这个命题进行证明．【答案】(1)，证明见解析；(2)见解析；(3)见解析【详解】（1）证明：（1）如图1，延长至F，使，连接，则，∴，∵平分∴，  ∵，∴，在和中，，∴，∴，∴．故答案为：．（2）证明：如图3，在上截取，使，连接∵分别平分，∴，∵，∴，在和中，，∴，∴，∴，∴，  ∴，∴，∴．（3）证明：如图4：延长至G，使，连接，则，∴，∵，∴，∵，  ∴，∴，∴，∴，在和中，，∴∴，即平分．12．在中，且．(1)如图（1），若分别平分，交于点C、B，连接．请你判断是否相等，并说明理由；(2)的位置保持不变，将（1）中的绕点A逆时针旋转至图（2）的位置，相交于O，请你判断线段与的位置关系及数量关系，并说明理由；(3)在（2）的条件下，若，试求四边形的面积．【答案】(1)，理由见解析；(2)，，理由见解析；(3)32【详解】（1）解：．理由如下：∵分别平分，∴，，∵，∴ ，在和中，∵，∴，∴；（2）解：，．理由如下：∵， ∴，即，在和中，∵，∴，∴，∴，∵，∴，∵，∴，∴；（3）解：∵，∴四边形的面积．13．在中，，点D是直线BC上一点（不与重合），以为一边在的右侧作，使，，连接．(1)如图1，当点D在线段上，如果，则为多少？说明理由；(2)设，．①如图2，当点D在线段上移动，则之间有怎样的数量关系？请说明理由；②当点D在直线上移动，则之间有怎样的数量关系？请写出你的结论，画出图形，简要证明．【答案】(1)；(2)①，②之间满足或【详解】（1）解：∵，∴，∵，∴，∴，在和中，，∴，∴，∴；（2）①，理由如下：∵，∴．即．在与中，，∴，∴．∴．∵，∴，∵，∴；②当点在的延长线上时，，理由如下：如图：∵，∴，∴，在和中，，∴，∴，∵，，∴，，∴，∴；当点D在线段的延长线上时，．理由如下：如图，∵，∴，即，在和中，，∴，∴，∴．∵，∴，∵，∴，综上：当点D在直线上移动时，之间满足或．14．如图，在中，，分别过点B，C作过点A的直线的垂线BD，CE，垂足为D，E．若，求DE的长． 【答案】7cm【详解】解：∵在中，，∴，∵，∴，∴，∴，又∵，∴，∴，∴．15．如图1，∠DAB＝90°，CD⊥AD于点D，点E是线段AD上的一点，若DE＝AB，DC＝AE．(1)判断CE与BE的关系是        ．(2)如图2，若点E在线段DA的延长线上，过点D在AD的另一侧作CD⊥AD，并保持CD＝AE，DE＝AB，连接CB，CE，BE，试说明（1）中结论是否成立，并说明理由．【答案】(1)CE＝BE且CE⊥BE；(2)成立，理由详见解析【解析】（1）解：CE＝BE且CE⊥BE，理由如下：∵CD⊥AD，∴∠CDE＝90°，∵∠DAB＝90°，∴∠CDE＝∠EAB，在△CDE和△EAB中，∴，∴CE＝BE，∠CED＝∠EBA，∵∠EBA＋∠BEA＝90°，∴∠CED＋∠BEA＝90°，∴∠CEB＝90°，∴CE⊥BE，∴CE＝BE且CE⊥BE．（2）解：（1）中结论成立，理由如下：∵CD⊥AD，∴∠CDE＝90°，∵∠DAB＝90°，∴∠CDE＝∠EAB，在△CDE和△EAB中，∴，∴CE＝BE，∠CED＝∠EBA，∵∠EBA＋∠BEA＝90°，∴∠CED＋∠BEA＝90°，∴∠CEB＝90°，∴CE⊥BE，∴CE＝BE且CE⊥BE．