福建省三明市将乐县2021-2022学年八年级上学期期中数学【试卷+答案】

这是一份福建省三明市将乐县2021-2022学年八年级上学期期中数学【试卷+答案】，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2021-2022学年福建省三明市将乐县八年级第一学期期中
数学试卷
一、选择题（本大题共10小题，每小题4分，计40分.在每小题给出的四个选项中，只有一项是符合题目要求的，请在答题卡的相应位置填涂）
1．下列各数中是无理数的是（　　）
A．2 B． C． D．
2．下列数据中不能作为直角三角形三边长的是（　　）
A．6、8、10 B．5、12、13 C．、、 D．1、1、
3．下列二次根式属于最简二次根式的是（　　）
A． B． C． D．
4．已知点P（m+3，m+1）在x轴上，则P点的坐标为（　　）
A．（0，2） B．（2，0） C．（4，0） D．（0，﹣4）
5．如图所示，已知数轴上的点A、B、C、D分别表示数﹣2、1、2、3，则表示的点P落在线段（　　）

A．AO上 B．OB上 C．BC上 D．CD上
6．下面计算正确的是（　　）
A． B． C． D．
7．在平面直角坐标系xOy中，点P（﹣3，5）关于y轴对称的点的坐标是（　　）
A．（﹣3，﹣5） B．（3，﹣5） C．（3，5） D．（5，﹣3）
8．对于函数y＝﹣x+3，下列说法错误的是（　　）
A．图象经过点（2，2）
B．y随着x的增大而减小
C．图象与y轴的交点是（6，0）
D．图象与坐标轴围成的三角形面积是9
9．已知正比例函数y＝kx（k≠0），函数值随x的增大而增大，则一次函数y＝﹣kx+k的图象大致是（　　）
A． B．
C． D．
10．一个小球从点A（3，3）出发，经过y轴上点C反弹后经过点B（1，0），则小球从A点经过点C到B点经过的最短路线长是（　　）
A．4 B．5 C．6 D．7
二、填空题：（本大题共6小题，每小题4分，计24分；请将答案填在答题卡的相应位置．）
11．9的算术平方根是　 　．
12．已知点P在第二象限，且到x轴的距离是2，到y轴的距离是5，则点P的坐标是　 　．
13．一个三角形的三边的比是3：4：5，它的周长是48，则它的面积是 　 　．
14．若一个正数的平方根是2a+1和﹣a﹣2，则这个正数是　 　．
15．如图，有一圆柱，其高为12cm，底面半径为3cm，在圆柱下底面A点处有一只蚂蚁，它想得到上底面B处的食物，则蚂蚁经过的最短距离为 　 　cm．（π取3）

16．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D．已知AB＝15，Rt△ABC的周长为15+9，则CD的长为 　 　．

三、解答题：（本大题共9小题，计86分．请将解答过程写在答题卡的相应位置.）
17．计算：
（1）；
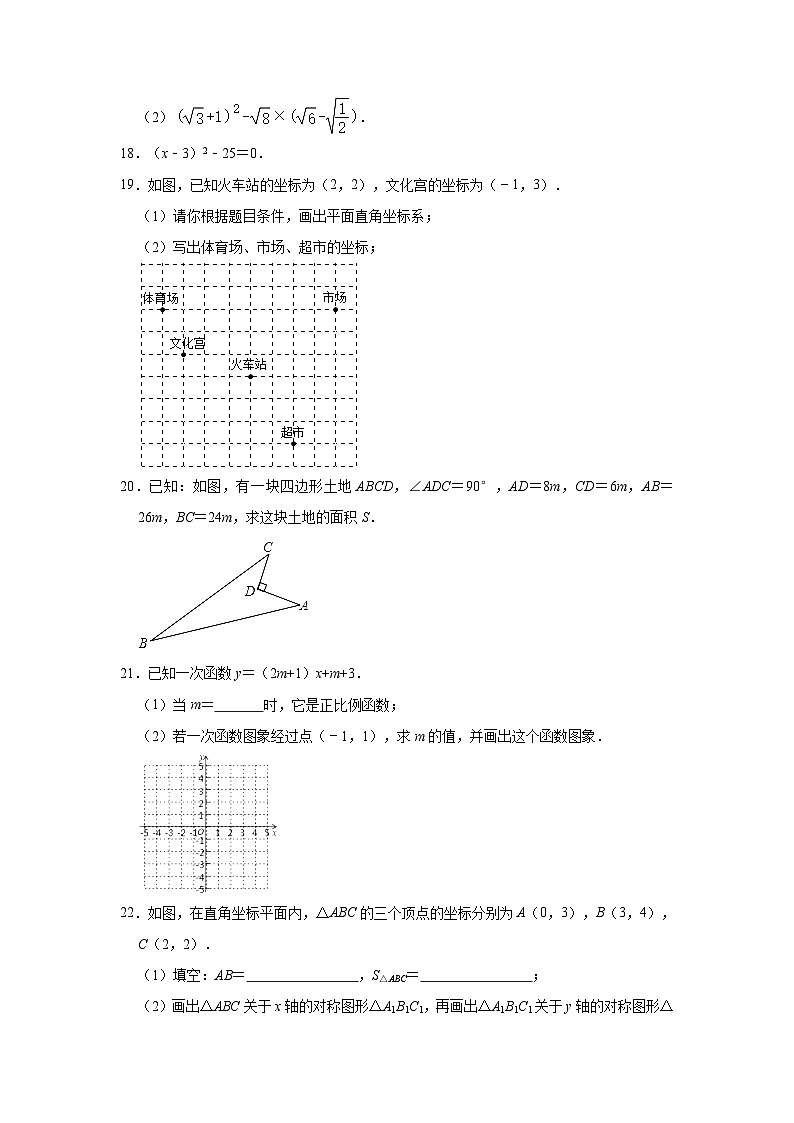
（2）．
18．（x﹣3）2﹣25＝0．
19．如图，已知火车站的坐标为（2，2），文化宫的坐标为（﹣1，3）．
（1）请你根据题目条件，画出平面直角坐标系；
（2）写出体育场、市场、超市的坐标；

20．已知：如图，有一块四边形土地ABCD，∠ADC＝90°，AD＝8m，CD＝6m，AB＝26m，BC＝24m，求这块土地的面积S．

21．已知一次函数y＝（2m+1）x+m+3．
（1）当m＝　 　时，它是正比例函数；
（2）若一次函数图象经过点（﹣1，1），求m的值，并画出这个函数图象．

22．如图，在直角坐标平面内，△ABC的三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）．
（1）填空：AB＝　 　，S△ABC＝　 　；
（2）画出△ABC关于x轴的对称图形△A1B1C1，再画出△A1B1C1关于y轴的对称图形△A2B2C2；
（3）若M是△ABC内一点，具坐标是（a，b），则△A2B2C2中，点M的对应点的坐标为　 　．

23．如图，将长方形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E．
（1）试判断△BDE的形状，并说明理由；
（2）若AB＝4，AD＝8，求△BDE的面积．

24．小明在解决问题：已知a＝，求2a2﹣8a+1的值，他是这样分析与解答的：
∵a＝，∴．
∴（a﹣2）2＝3，即a2﹣4a+4＝3．
∴a2﹣4a＝﹣1，∴2a2﹣8a+1＝2（a2﹣4a）+1＝2×（﹣1）+1＝﹣1．
请你根据小明的分析过程，解决如下问题：
（1）填空：＝　 　，＝　 　；
（2）计算：；
（3）若a＝，求2a2﹣12a﹣5的值．
25．如图，直线l1：y1＝﹣x+2与x轴，y轴分别交于A，B两点，点P（m，3）为直线l1上一点，另一直线l2：y2＝x+b过点P，与x轴交于点C．
（1）直接写出m和b的值及点A、点C的坐标；
（2）若动点Q从点C开始以每秒1个单位的速度向x轴正方向移动．设点Q的运动时间为t秒．
①当点Q在运动过程中，请直接写出△APQ的面积S与t的函数关系式；
②求出当t为多少时，△APQ的面积等于3；
③是否存在t的值，使△APQ为等腰三角形？若存在，请直接写出t的值；若不存在，请说明理由．



参考答案
一、选择题（本大题共10小题，每小题4分，计40分.在每小题给出的四个选项中，只有一项是符合题目要求的，请在答题卡的相应位置填涂）
1．下列各数中是无理数的是（　　）
A．2 B． C． D．
【分析】由于无理数就是无限不循环小数．初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及0.1010010001…，等有这样规律的数．由此即可判定选择项．
解：∵A、2是有理数，故选项错误；
B、是开方开不尽的数，是无理数，故选项正确；
C、＝﹣2，是有理数，故选项错误；
D、是整数或分数，是有理数，故选项错误．
故选：B．
2．下列数据中不能作为直角三角形三边长的是（　　）
A．6、8、10 B．5、12、13 C．、、 D．1、1、
【分析】利用勾股定理逆定理进行分析即可．
解：A、62+82＝102，能构成直角三角形，故此选项不合题意；
B、52+122＝132，能构成直角三角形，故此选项不符合题意；
C、（）2+（）2≠（）2，不能构成直角三角形，故此选项符合题意；
D、12+12＝（）2，能构成直角三角形，故此选项不合题意．
故选：C．
3．下列二次根式属于最简二次根式的是（　　）
A． B． C． D．
【分析】根据最简二次根式的定义逐个判断即可．
解：A．是最简二次根式，故本选项符合题意；
B．的被开方数中含有能开得尽方的因数，不是最简二次根式，故本选项不符合题意；
C．的被开方数中的因数不是整数，不是最简二次根式，故本选项不符合题意；
D．的被开方数中的因数不是整数，不是最简二次根式，故本选项不符合题意；
故选：A．
4．已知点P（m+3，m+1）在x轴上，则P点的坐标为（　　）
A．（0，2） B．（2，0） C．（4，0） D．（0，﹣4）
【分析】根据点P在x轴上，即y＝0，可得出m的值，从而得出点P的坐标．
解：∵点P（m+3，m+1）在x轴上，
∴y＝0，
∴m+1＝0，
解得m＝﹣1，
∴m+3＝﹣1+3＝2，
∴点P的坐标为（2，0）．
故选：B．
5．如图所示，已知数轴上的点A、B、C、D分别表示数﹣2、1、2、3，则表示的点P落在线段（　　）

A．AO上 B．OB上 C．BC上 D．CD上
【分析】估算出的大小，即可确定出结果．
解：∵4＜5＜9，
∴2＜＜3，即﹣3＜﹣2，
∴1＜2，
∴表示的点P落在线段BC上．
故选：C．
6．下面计算正确的是（　　）
A． B． C． D．
【分析】利用二次根式的加减法对A、C进行判断；根据算术平方根的定义对B进行判断；根据二次根式的除法法则对D进行判断．
解：A．3与不能合并，所以A选项不符合题意；
B． ＝2，所以B选项不符合题意；
C． 与不能合并，所以C选项不符合题意；
D． ÷＝＝3，所以D选项符合题意；
故选：D．
7．在平面直角坐标系xOy中，点P（﹣3，5）关于y轴对称的点的坐标是（　　）
A．（﹣3，﹣5） B．（3，﹣5） C．（3，5） D．（5，﹣3）
【分析】直接利用关于y轴对称点的性质得出答案．
解：点P（﹣3，5）关于y轴对称的点的坐标是：（3，5）．
故选：C．
8．对于函数y＝﹣x+3，下列说法错误的是（　　）
A．图象经过点（2，2）
B．y随着x的增大而减小
C．图象与y轴的交点是（6，0）
D．图象与坐标轴围成的三角形面积是9
【分析】根据一次函数的性质进行计算即可．
解：A、函数y＝﹣x+3经过点（2，2），故正确，不符合题意；
B、y随着x的增大而减小，故正确，不符合题意；
C、图象与y轴的交点是（0，3），故错误，符合题意；
D、图象与坐标轴围成的三角形面积是9，故正确，不符合题意；
故选：C．
9．已知正比例函数y＝kx（k≠0），函数值随x的增大而增大，则一次函数y＝﹣kx+k的图象大致是（　　）
A． B．
C． D．
【分析】由于正比例函数y＝kx（k≠0）函数值随x的增大而增大，可得k＞0，﹣k＜0，然后，判断一次函数y＝﹣kx+k的图象经过象限即可．
解：∵正比例函数y＝kx（k≠0）函数值随x的增大而增大，
∴k＞0，
∴﹣k＜0，
∴一次函数y＝﹣kx+k的图象经过一、二、四象限；
故选：A．
10．一个小球从点A（3，3）出发，经过y轴上点C反弹后经过点B（1，0），则小球从A点经过点C到B点经过的最短路线长是（　　）
A．4 B．5 C．6 D．7
【分析】如果设A点关于y轴的对称点为A′，那么C点就是A′B与y轴的交点．易知A′（﹣3，3），又B（1，0），可用待定系数法求出直线A′B的方程．再求出C点坐标，根据勾股定理分别求出AC、BC的长度．那么小球路线从A点到B点经过的路线长是AC+BC，从而得出结果．
解：如果将y轴当成平面镜，设A点关于y轴的对称点为A′，则由小球路线知识可知，A′相当于A的像点，光线从A到C到B，相当于小球路线从A′直接到B，所以C点就是A′B与y轴的交点．
∵A点关于y轴的对称点为A′，A（3，3），
∴A′（﹣3，3），
进而由两点式写出A′B的直线方程为：y＝﹣（x﹣1）．
令x＝0，求得y＝．所以C点坐标为（0，）．
那么根据勾股定理，可得：
AC＝，BC＝．
因此，AC+BC＝5．
故选：B．
二、填空题：（本大题共6小题，每小题4分，计24分；请将答案填在答题卡的相应位置．）
11．9的算术平方根是　3　．
【分析】9的平方根为±3，算术平方根为非负，从而得出结论．
解：∵（±3）2＝9，
∴9的算术平方根是3．
故答案为：3．
12．已知点P在第二象限，且到x轴的距离是2，到y轴的距离是5，则点P的坐标是　（﹣5，2）　．
【分析】由点P在第二象限可知横坐标为负，纵坐标为正，然后根据点P到两坐标轴的距离确定出点P的坐标即可．
解：∵x轴的距离为2，到y轴的距离为5，
∴点的纵坐标是±2，横坐标是±5，
又∵第二象限内的点横坐标小于0，纵坐标大于0，
∴点的横坐标是﹣5，纵坐标是2．
故此点的坐标为（﹣5，2）．
故答案为：（﹣5，2）．
13．一个三角形的三边的比是3：4：5，它的周长是48，则它的面积是 　96　．
【分析】可设三角形的三边分别为3x，4x和5x，利用周长可求得x的值，则可求得三角形的三边长．
解：∵三角形三边的比为3：4：5，
∴可设三角形的三边分别为3x，4x和5x，
由题意可知3x+4x+5x＝48，解得x＝4，
∴三角形三边的长分别为12、16、20，
∵122+162＝202，
∴三角形是直角三角形，
∴三角形的面积＝，
故答案为：96．
14．若一个正数的平方根是2a+1和﹣a﹣2，则这个正数是　9　．
【分析】根据正数的平方根有两个，且互为相反数，求出a的值，即可确定出这个正数．
解：根据题意得：2a+1﹣a﹣2＝0，
解得：a＝1，
可得正数平方根为3和﹣3，
则这个正数为9．
故答案为：9
15．如图，有一圆柱，其高为12cm，底面半径为3cm，在圆柱下底面A点处有一只蚂蚁，它想得到上底面B处的食物，则蚂蚁经过的最短距离为 　15　cm．（π取3）

【分析】本题应先把圆柱展开即得其平面展开图，则A，B所在的长方形的长为圆柱的高12cm，宽为底面圆周长的一半为πr，蚂蚁经过的最短距离为连接A，B的线段长，由勾股定理求得AB的长．
解：圆柱展开图为长方形，
则A，B所在的长方形的长为圆柱的高12cm，宽为底面圆周长的一半为πrcm，
蚂蚁经过的最短距离为连接A，B的线段长，
由勾股定理得AB＝＝＝＝15cm．
故蚂蚁经过的最短距离为15cm．

16．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D．已知AB＝15，Rt△ABC的周长为15+9，则CD的长为 　6　．

【分析】由已知条件得出AC+BC＝9，由勾股定理得出AC2+BC2＝AB2＝152＝225，求出AC×BC＝90，由三角形ABC的面积即可得出答案．
解：如图所示：

∵Rt△ABC的周长为15+9，∠ACB＝90°，AB＝15，
∴AC+BC＝9，AC2+BC2＝AB2＝152＝225，
∴（AC+BC）2＝（9）2，即AC2+2AC×BC+BC2＝405，
∴2AC×BC＝405﹣225＝180，
∴AC×BC＝90，
∵S△ABC＝AB×CD＝AC×BC，
∴CD＝＝6；
故答案为：6．
三、解答题：（本大题共9小题，计86分．请将解答过程写在答题卡的相应位置.）
17．计算：
（1）；
（2）．
【分析】（1）利用二次根式的除法法则运算；
（2）先利用完全平方公式和二次根式的乘法法则运算，然后化简后合并即可．
解：（1）原式＝﹣
＝5﹣4
＝1；
（2）原式＝3+2+1﹣+
＝4+2﹣+
＝4+2﹣4+2
＝6﹣2．
18．（x﹣3）2﹣25＝0．
【分析】根据直接开平方，可得答案．
解：移项，得
（x﹣3）2＝25，
开方，得
x﹣3＝±5，
x1＝3+5＝8，x2＝3﹣5＝﹣2．
19．如图，已知火车站的坐标为（2，2），文化宫的坐标为（﹣1，3）．
（1）请你根据题目条件，画出平面直角坐标系；
（2）写出体育场、市场、超市的坐标；

【分析】（1）首先根据火车站的坐标确定原点位置，然后再画出坐标系即可；
（2）根据坐标系确定体育场、市场、超市的坐标即可．
解：（1）如图所示：

（2）体育场（﹣2，5），市场（6，5），超市（4，﹣1）．

20．已知：如图，有一块四边形土地ABCD，∠ADC＝90°，AD＝8m，CD＝6m，AB＝26m，BC＝24m，求这块土地的面积S．

【分析】连接AC，根据解直角△ADC求AC，求证△ACB为直角三角形，根据四边形ABCD的面积＝△ABC面积﹣△ACD面积即可计算．
解：如图，连接AC．
在Rt△ACD中，由勾股定理，得AC2＝AD2+DC2＝82+62，所以AC＝10．
在△ABC中，由AB2﹣BC2＝262﹣242＝100，
即AC2+BC2＝AB2．
所以△ABC为直角三角形，∠ACB＝90°．则

所以这块地的面积为96m2．

21．已知一次函数y＝（2m+1）x+m+3．
（1）当m＝　﹣3　时，它是正比例函数；
（2）若一次函数图象经过点（﹣1，1），求m的值，并画出这个函数图象．

【分析】（1）根据正比例函数的定义求解即可．
（2）根据待定系数法即可求得．
解：（1）∵函数y＝（2m+1）x+m+3是正比例函数，
∴m+3＝0，
解得m＝﹣3，
∴当m＝﹣3时，它是正比例函数；
故答案为﹣3；
（2）一次函数y＝（2m+1）x+m+3图象经过点（﹣1，1），
∴1＝﹣2m﹣1+m+3，
∴m＝1，
∴y＝3x+4，
令x＝0，在y＝4，
画出函数的图象如图，
．
22．如图，在直角坐标平面内，△ABC的三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）．
（1）填空：AB＝　　，S△ABC＝　　；
（2）画出△ABC关于x轴的对称图形△A1B1C1，再画出△A1B1C1关于y轴的对称图形△A2B2C2；
（3）若M是△ABC内一点，具坐标是（a，b），则△A2B2C2中，点M的对应点的坐标为　（﹣a，﹣b）　．

【分析】（1）依据勾股定理以及割补法进行计算，即可得出结论；
（2）依据轴对称的性质，即可得到△ABC关于x轴的对称图形△A1B1C1，△A1B1C1关于y轴的对称图形△A2B2C2；
（3）依据关于坐标轴对称的点的坐标特征，即可得到点M的对应点的坐标．
解：（1）AB＝＝，
S△ABC＝2×3﹣×1×3﹣×1×2×2＝；
故答案为：，；
（2）如图所示，△A1B1C1，△A2B2C2即为所求；

（3）∵M是△ABC内一点，具坐标是（a，b），
∴△A2B2C2中，点M的对应点的坐标为（﹣a，﹣b）．
故答案为：（﹣a，﹣b）．
23．如图，将长方形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E．
（1）试判断△BDE的形状，并说明理由；
（2）若AB＝4，AD＝8，求△BDE的面积．

【分析】（1）由折叠可知，∠CBD＝∠EBD，再由AD∥BC，得到∠CBD＝∠EDB，即可得到∠EBD＝∠EDB，于是得到BE＝DE，等腰三角形即可证明；
（2）设DE＝x，则BE＝x，AE＝8﹣x，在Rt△ABE中，由勾股定理求出x的值，再由三角形的面积公式求出面积的值．
解：（1）△BDE是等腰三角形．
由折叠可知，∠CBD＝∠EBD，
∵AD∥BC，
∴∠CBD＝∠EDB，
∴∠EBD＝∠EDB，
∴BE＝DE，
即△BDE是等腰三角形；

（2）设DE＝x，则BE＝x，AE＝8﹣x，
在Rt△ABE中，由勾股定理得：AB2+AE2＝BE2即42+（8﹣x）2＝x2，
解得：x＝5，
所以S△BDE＝DE×AB＝×5×4＝10．
24．小明在解决问题：已知a＝，求2a2﹣8a+1的值，他是这样分析与解答的：
∵a＝，∴．
∴（a﹣2）2＝3，即a2﹣4a+4＝3．
∴a2﹣4a＝﹣1，∴2a2﹣8a+1＝2（a2﹣4a）+1＝2×（﹣1）+1＝﹣1．
请你根据小明的分析过程，解决如下问题：
（1）填空：＝　　，＝　　；
（2）计算：；
（3）若a＝，求2a2﹣12a﹣5的值．
【分析】（1）利用平方差公式进行二次根式的分母有理化计算；
（2）根据二次根式的分母有理化计算发现数字的变化规律，从而进行计算；
（3）先对字母a的值进行二次根式的分母有理化计算，然后代入求值．
解：（1）＝＝，
＝，
故答案为：，；
（2）原式＝（﹣1++...+）
＝（）（）
＝2021﹣1
＝2020；
（3）当a＝＝时，
原式＝2（）2﹣12（）﹣5
＝2（10+6+9）﹣12﹣36﹣5
＝20+12+18﹣12﹣36﹣5
＝﹣3．
25．如图，直线l1：y1＝﹣x+2与x轴，y轴分别交于A，B两点，点P（m，3）为直线l1上一点，另一直线l2：y2＝x+b过点P，与x轴交于点C．
（1）直接写出m和b的值及点A、点C的坐标；
（2）若动点Q从点C开始以每秒1个单位的速度向x轴正方向移动．设点Q的运动时间为t秒．
①当点Q在运动过程中，请直接写出△APQ的面积S与t的函数关系式；
②求出当t为多少时，△APQ的面积等于3；
③是否存在t的值，使△APQ为等腰三角形？若存在，请直接写出t的值；若不存在，请说明理由．

【分析】（1）把点P坐标代入直线l1解析式可求得m，可求得P点坐标，代入直线l2可求得b，可求得直线l2的解析式，在y1＝0可求得A点坐标，令y2＝0可求得相应x的值，可求得C点坐标；
（2）①分点Q在A、C之间和点Q在A的右边两种情况，分别用t可表示出AQ，则可表示出S；
②令S＝3可求得t的值；
③可设出Q坐标为（x，0），用x可分别表示出PQ、AQ和AP的长，分PQ＝AQ、PQ＝AP和AQ＝AP三种情况可得到关于的方程，可求得相应的x的值，则可求得Q点的坐标，则可求得CQ的长，可求得t的值．
解：
（1）∵点P在直线l1上，
∴3＝﹣m+2，解得m＝﹣1，
∴P（﹣1，3），
∵y2＝x+b过点P，
∴3＝×（﹣1）+b，解得b＝，
∴直线y2＝x+，令y2＝0可得0＝x+，解得x＝﹣7，
∴点C坐标为（﹣7，0），
在y1＝﹣x+2中，令y1＝0可得﹣x+2＝0，解得x＝2，
∴A点坐标为（2，0）；
（2）①由题意可知CQ＝t，P到x轴的距离为3，
∵A（2，0），C（﹣7，0），
∴AC＝2﹣（﹣7）＝9，
当Q在A、C之间时，则AQ＝AC﹣CQ＝9﹣t，
∴S＝×3×（9﹣t）＝﹣t+；
当Q在A的右边时，则AQ＝CQ﹣AC＝t﹣9，
∴S＝×3×（t﹣9）＝t﹣；
②令S＝3可得﹣t+＝3或t﹣＝3，解得t＝7或t＝11，
即当t的值为7秒或11秒时△APQ的面积等于3；
③设Q（x，0）（x≥﹣7），
∵A（2，0），P（﹣1，3），
∴PQ2＝（x+1）2+32＝x2+2x+10，AQ2＝（x﹣2）2＝x2﹣4x+4，AP2＝（2+1）2+32＝18，
∵△APQ为等腰三角形，
∴有PQ＝AQ、PQ＝AP和AQ＝AP三种情况，
当PQ＝AQ时，则PQ2＝AQ2，即x2+2x+10＝x2﹣4x+4，解得x＝﹣1，则Q点坐标为（﹣1，0），
∴CQ＝﹣1﹣（﹣7）＝6，即t＝6；
当PQ＝AP时，则PQ2＝AP2，即x2+2x+10＝18，解得x＝﹣4或x＝2，则Q点坐标为（﹣4，0）或（2，0）（与A点重合，舍去），
∴CQ＝﹣4﹣（﹣7）＝3，即t＝3；
当AQ＝AP时，则AQ2＝AP2，即x2﹣4x+4＝18，解得x＝2±3，则Q点坐标为（2+3，0）或（2﹣3，0），
∴CQ＝2+3﹣（﹣7）＝9+3或CQ＝2﹣3﹣（﹣7）＝9﹣3，即t＝9+3或t＝9﹣3；
综上可知存在满足条件的t，其值为6或3或t＝9+3或t＝9﹣3．