河南省邓州市2021-2022学年九年级上学期期中质量评估数学【试卷+答案】

邓州市2021∽2022学年第一学期期中质量评估九年级

                数学试卷

注意事项：1.本试卷共6页，三个大答题，满分120分，答题时间100分钟；

2. 请按答题卡上注意事项的要求直接把答案填写在答题卡上，答在试卷上的答案无效.

一、选择题（每小题3分，共30分）请将唯一正确答案的序号涂在答题卡上.

1.下列根式中，不是最简二次根式的是（　　）

A． B． C． D．

2．下列各式化简后能与合并的是（　　）.

A． B． C． D．

3．下列各式中，运算正确的是（　　）.

A．＝±9       B．×＝9   C．＝3   D．

4．用配方法解方程x2﹣2x-1＝0，则方程可变形为（　　）.

A．=1  B．=2   C．=1    D．=2

5．一元二次方程（x+1）（x-5）＝3x-18的根的情况是（　　）.

A．没有实数根 B．有两个相等的实数根 

C．有两个不相等的实数根 D．只有一个实数根

6．在△ABC中，∠ACB＝90°，用直尺和圆规在AB上确定点D，使△ACD∽△CBD，根据作图痕迹判断，正确的是（　　）.

A． B． 

C． D．

7．给出一种运算：对于函数y＝xn，规定y'＝n×xn﹣1．若函数y＝x4，则有y'＝4×x3，已知函数y＝x3，则方程y'＝6x的解是（　　）.

A．x＝0 B．x＝2 C．x1＝0，x2＝2 D．x1＝0，x2＝﹣2

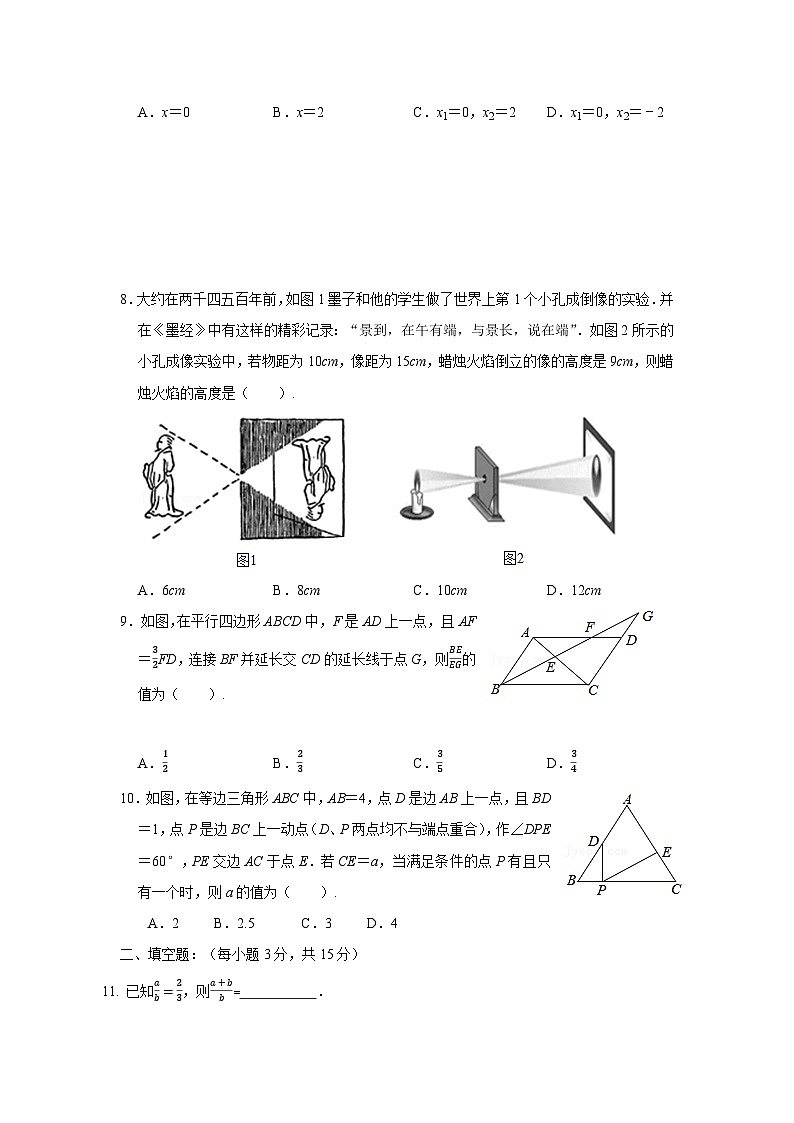
8．大约在两千四五百年前，如图1墨子和他的学生做了世界上第1个小孔成倒像的实验．并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”．如图2所示的小孔成像实验中，若物距为10cm，像距为15cm，蜡烛火焰倒立的像的高度是9cm，则蜡烛火焰的高度是（　　）.

A．6cm B．8cm C．10cm D．12cm

9．如图，在平行四边形ABCD中，F是AD上一点，且AF＝FD，连接BF并延长交CD的延长线于点G，则的值为（　　）.

A． B． C． D．

10．如图，在等边三角形ABC中，AB＝4，点D是边AB上一点，且BD＝1，点P是边BC上一动点（D、P两点均不与端点重合），作∠DPE＝60°，PE交边AC于点E．若CE＝a，当满足条件的点P有且只有一个时，则a的值为（　　）.

A．2     B．2.5     C．3     D．4

二、填空题：（每小题3分，共15分）

11. 已知，则=　         ．

12.方程+x-1=0的一个正数根是　           ．

13．“杂交水稻之父”袁隆平为提高水稻的产量奉献了自己的一生．某村种植了杂交水稻2018年的平均亩产300千克，2020年平均亩产363千克，则此水稻亩产量的平均增长率为 　    　．

14．清朝《数理精蕴》里有一首小诗《古色古香方城池》：今有一座古方城，四面正中都开门，南门直行八里止，脚下有座塔耸立．又出西门二里停，切城角恰见塔形，请问诸君能算者，方城每边长是几？如图所示，诗的意思是：有正方形的城池一座，四面城墙的正中有门，从南门口（点D）直行8里有一塔（点A），自西门（点E）直行2里至点B，切城角（点C）也可以看见塔，问这座方城每面城墙的长是　 　里．

15．如图，边长为2的正方形ABCD中，点E为AD的中点．连接BE，将△ABE沿BE折叠得到△FBE，BF交AC于点G，则AG的长为        ．

三、解答题：（本大题8个小题，共75分）

16.(每小题4分，共8分）计算或解方程

（1）（-）-（-）；

（2）2x2＝2x+1．

17．（9分）2021年7月1日是建党100周年纪念日，在本月日历表上可以用一个方框圈出4个数（如图所示），若圈出的四个数中，最小数与最大数的乘积为48，求这个最小数（请用方程知识解答）．

18．（9分）定义新运算：对于任意实数a，b，都有a⊕b＝a（a﹣b）+1，等式右边是通常的加法、减法及乘法运算，比如：2⊕5＝2×（2﹣5）+1＝2×（﹣3）+1＝﹣6+1＝﹣5．

（1）若x⊕（﹣2）＝25，求x的值；(5分）

（2）若3⊕a的值小于10，请判断方程x2+bx﹣a＝0的根的情况．（4分）

19．（9分）如图，已知△ABC，AB＝2，BC＝5，且∠ABC＝2∠C，为了求边AC的长，聪明的小亮想出了一个好办法，将边BC反向延长至点D，使DB＝AB，连接AD，从而小亮发现图中存在一对相似三角形，问题便迎刃而解了！

（1）请你找出图中存在的一对相似三角形，并进行证明.

（2）求边AC的长．

20．（9分）如图，某同学正向着教学楼（AB）走去，他发现教学楼后面有一座5G信号接收塔（DC），可过了一会抬头一看：“怎么看不到接收塔了？”心里很是纳闷．经过了解，教学楼、接收塔的高分别是21.6m和31.6m，它们之间的距离为32m，该同学的眼睛距地面高度（EF）是1.6m．当他刚发现接收塔的顶部D恰好被教学楼的顶部A挡住时，他与教学楼（AB）之间的距离为多少米？

21．（10分）某药店新进一批桶装消毒液，每桶进价35元，原计划以每桶55元的价格销售，为更好地助力疫情防控，现决定降价销售．已知这种消毒液销售量y（桶）与每桶降价x（元）（0＜x＜20）之间满足一次函数关系y＝kx+b（k），其图象如图所示：

（1）求y与x之间的函数关系式,并解释k的实际意义.

（2）在这次助力疫情防控活动中，该药店仅获利1890元．这种消毒液每桶实际售价多少元？

22．（10分）如图，已知A、B两点的坐标分别为（8，0）和（0，6），动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动、动直线EF从x轴开始以每秒1个单位的速度向上平行移动（即EF∥x轴），并且分别与y轴、线段AB交于点E、F，连接EP、FP，设动点P与动直线EF同时出发，运动时间为t秒．

（1）求t＝3时，△PEF的面积；

（2）直线EF、点P在运动过程中，是否存在这样的t值，使得△PEF的面积等于8（平方单位）？若存在，请求出此时t的值；若不存在，请说明理由．

（3）当t为何值时，△EOP与△BOA相似．

23．（11分）如图1，在△ABC中，∠ACB＝90°，AC＝BC，点D是AB边上一动点（含端点A、B），过点B作BE垂直于射线CD，垂足为E，点F在射线CD上，且EF＝BE，连接AF、BF．

（1）求证：△ABF∽△CBE；

（2）如图2，连接AE，点P、M、N分别为线段AC、AE、EF的中点，连接PM、MN、PN．求的值及∠PMN的度数；

（3）在（2）的条件下，若AB＝8，请直接写出PM的最大值．

邓州市2021∽2022学年第一学期期中质量评估九年级数学试卷

 参考答案及评分标准

一、选择题（每小题3分，共30分）

1.C  2.A   3.D  4.B  5.A    6.B   7. C  8. A  9.C    10.D

二、填空题：（每小题3分，共15分）

 11.     12.     13.10%．  14. 8    15.

三、解答题（本大题8个小题，共75分）

16.(每小题4分，共8分）

解：（1）原式＝（2﹣）﹣（-）.......................2分

＝2﹣﹣+.......................3分

＝3﹣；......................4分

（2）解：原方程可化为2x2﹣2x﹣1＝0，.......................1分

∵a＝2，b＝﹣2，c＝﹣1，

∴b2﹣4ac＝（﹣2）2﹣4×2×（﹣1）＝4+8＝12＞0，.......................2分

∴x＝＝＝，.......................3分

即x1＝，x2＝．......................4分

17．（9分）解：设这个最小数为x，则最大数为（x+8），

依题意得：x（x+8）＝48，.......................5分

整理得：x2+8x﹣48＝0，

解得：x1＝4，x2＝﹣12（不合题意，舍去）．.......................8分

答：这个最小数为4．......................9分

18.（9分）解：（1）∵a⊕b＝a（a﹣b）+1，x⊕（﹣2）＝4，

∴x（x+2）+1＝25，...........................3分

∴x2+2x﹣24＝0，

解得：x1＝4，x2＝﹣6，...........................4分

∴x的值为4或﹣6；...........................5分

（2）由题意得：3（3﹣a）+1＜10，解得：a＞0，...........................7分

∴b2﹣4×1×（﹣a）＝b2+4a＞0，...........................8分

∴方程有两个不相等的实数根．...........................9分

19.（9分）解：（1）存在的一对相似三角形是：△DBA∽△DAC.........................1分

证明：∵DB＝AB，∴∠D＝∠DAB

∴∠ABC=2∠D＝2∠DAB

∵∠ABC＝2∠C，∴∠D＝∠DAB＝∠C，.........................3分

又∵∠D＝∠D，........................4分

∴△DBA∽△DAC；.........................5分

（2）∵AB＝2，BC＝5，DB＝AB，

∴DB＝2，CD＝BC+DB＝7，.........................6分

∵△DBA∽△DAC，∴DB：DA＝DA：DC，∴2：DA＝DA：7，

解得DA＝，.........................8分

由（1）知∠D＝∠C，∴DA＝AC，

∴AC＝．.........................9分

20.（9分）解：如图，过E作EG⊥CD交AB于H，CD于G，

根据题意可得：四边形EFCG是矩形，........................2分

∴EF＝HB＝CG＝1.6m，EH＝FB，HG＝BC＝30m，

∴AH＝20m，DG＝30m，.......................3分

由AH∥DG得：△AEH∽△DEG，

∴，.......................6分

即∴．∴EH＝64．.......................8分

答：某同学与教学楼（AB）之间的距离为64米．.......................9分

21.解：（1）将点（1，110）、（3，130）代入一次函数表达式y＝kx+b得：，

解得：，

故函数的表达式为：y＝10x+100；......................3分

k的实际意义：这种消毒液每桶降价1元，销售量将增加10桶.......................4分

（2）由题意得：（10x+100）×（55﹣x﹣35）＝1890，.......................6分

整理，得x2﹣10x﹣11＝0．

解得x1＝11，x2＝﹣1（舍去）．......................9分

所以55﹣x＝44．

答：这种消毒液每桶实际售价44元．......................10分

22.(10分）解：（1）当t＝3时，OE＝BE＝3，OA＝8，OB＝6，

∵EF∥OA，∴△BEF∽△BOA，

∴，即=  ∴EF=4............................1分

∴S△PEF＝EF•OE＝（平方单位）；............................2分

（2）∵△BEF∽△BOA，

∴，即=∴EF=8t

∴............................4分

整理，得t2﹣6t+12＝0，

∵Δ＝﹣4×1×12＝﹣12＜0，

∴方程没有实数根．

∴不存在t值使得△PEF的面积等于8平方单位）.............................6分

（3）当∠EPO＝∠BAO时，△EOP∽△BOA，

∴，即=

解得t＝2.4；.............................8分

当∠EPO＝∠ABO时，△EOP∽△AOB，

∴，即=

解得t＝．

∴当t＝2.4或时，△EOP与△BOA相似．.............................10分

23.(11分）（1）证明：如图1中，

∵CA＝CB，∠ACB＝90°，EF＝EB，∠BEF＝90°，

∴∠CBA＝∠EBF＝45°，AB＝BC，BF＝BE，

∴∠CBE＝∠ABF，＝＝，

∴△ABF∽△CBE．....................................3分

（2） 解：∵△ABF∽△CBE，

∴＝＝，

∴AF＝EC，

由题意知MN是△AEF的中位线

MN=AF同理 PM=CE;

 ===....................................6分

延长PM交AF于点T.                 

∵BE⊥CF， ∴∠CEB＝90°，

∵△ABF∽△CBE，∴∠CEB＝∠AFB＝90°，

∵∠EFB＝45°，∴∠AFC＝45°，

∵MN是△AEF的中位线∴MN∥AF，同理MP∥CF∴四边形MNFT是平行四边形，

∴∠TMN＝∠AFC＝45°，

∴∠PMN＝135°....................................9分

(3)PM的最大值=2......................................11分

提示：当点E与B重合时，EC的值最大，EC的最大值为= 4，

此时PM的最大值=2.