河南省许昌市禹州市2022-2023学年八年级下学期期中考试数学试卷

这是一份河南省许昌市禹州市2022-2023学年八年级下学期期中考试数学试卷，共14页。试卷主要包含了解答题等内容，欢迎下载使用。
2022-2023学年河南省许昌市禹州市八年级（下）期中数学试卷
一、选择题（每小题3分，共30分）下列各小题均有四个答案，其中只有一个是正确的.
1．（3分）下列根式是最简二次根式的是（　　）
A． B． C． D．
2．（3分）在△ABC中，∠A，∠B，∠C的对边分别为a，b，c，且 （a+c）（a﹣c）＝b2，则（　　）
A．∠A为直角 B．∠B为直角 C．∠C为直角 D．∠A是锐角
3．（3分）已知1＜a＜2，则化简 的结果为（　　）
A．2a﹣4 B．4﹣2a C．2 D．﹣2
4．（3分）计算÷× 的结果是（　　）
A． B． C． D．
5．（3分）下列命题中，其逆命题成立的是（　　）
A．对顶角相等
B．若ac2＞bc2，则a＞b
C．直角三角形的两锐角互余
D．全等三角形的对应角相等
6．（3分）如图，长方形ABCD的顶点A，B在数轴上，点A表示﹣1，AB＝3，AD＝1．若以点A为圆心，对角线AC长为半径作弧，交数轴正半轴于点M，则点M所表示的数为（　　）

A． B． C． D．
7．（3分）依据所标数据，一定为平行四边形的是（　　）
A．
B．
C．
D．
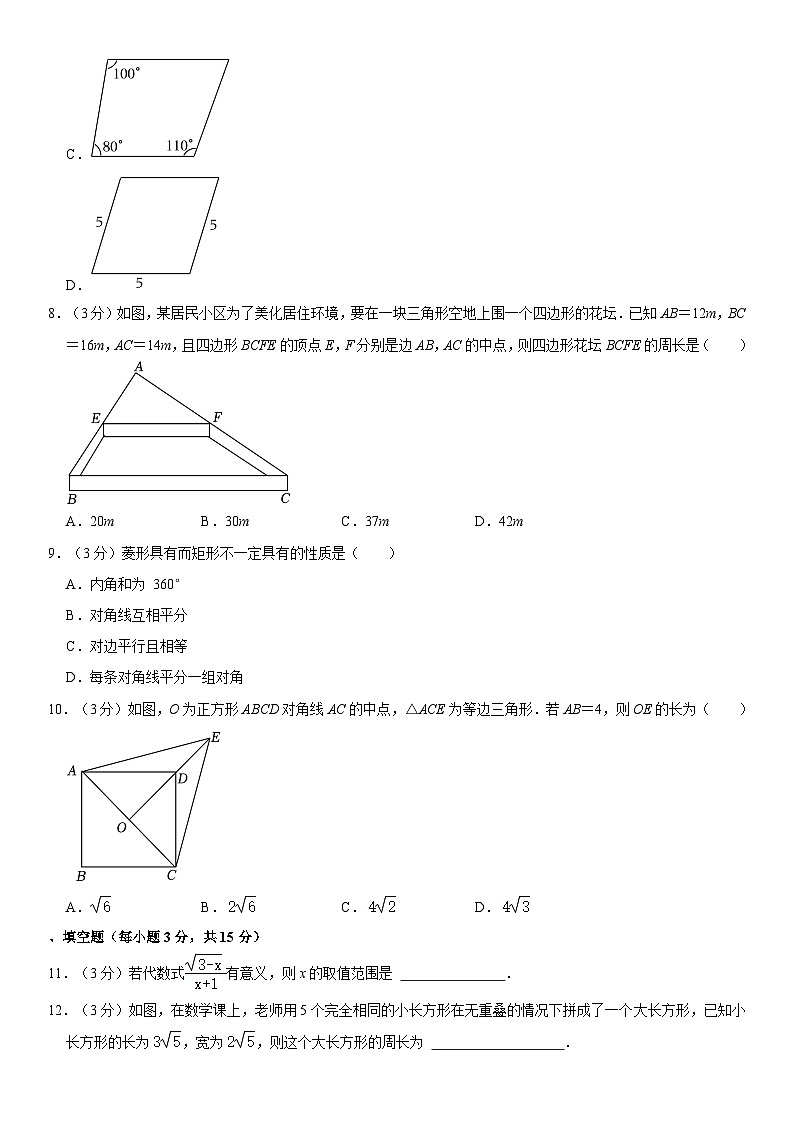
8．（3分）如图，某居民小区为了美化居住环境，要在一块三角形空地上围一个四边形的花坛．已知AB＝12m，BC＝16m，AC＝14m，且四边形BCFE的顶点E，F分别是边AB，AC的中点，则四边形花坛BCFE的周长是（　　）

A．20m B．30m C．37m D．42m
9．（3分）菱形具有而矩形不一定具有的性质是（　　）
A．内角和为 360°
B．对角线互相平分
C．对边平行且相等
D．每条对角线平分一组对角
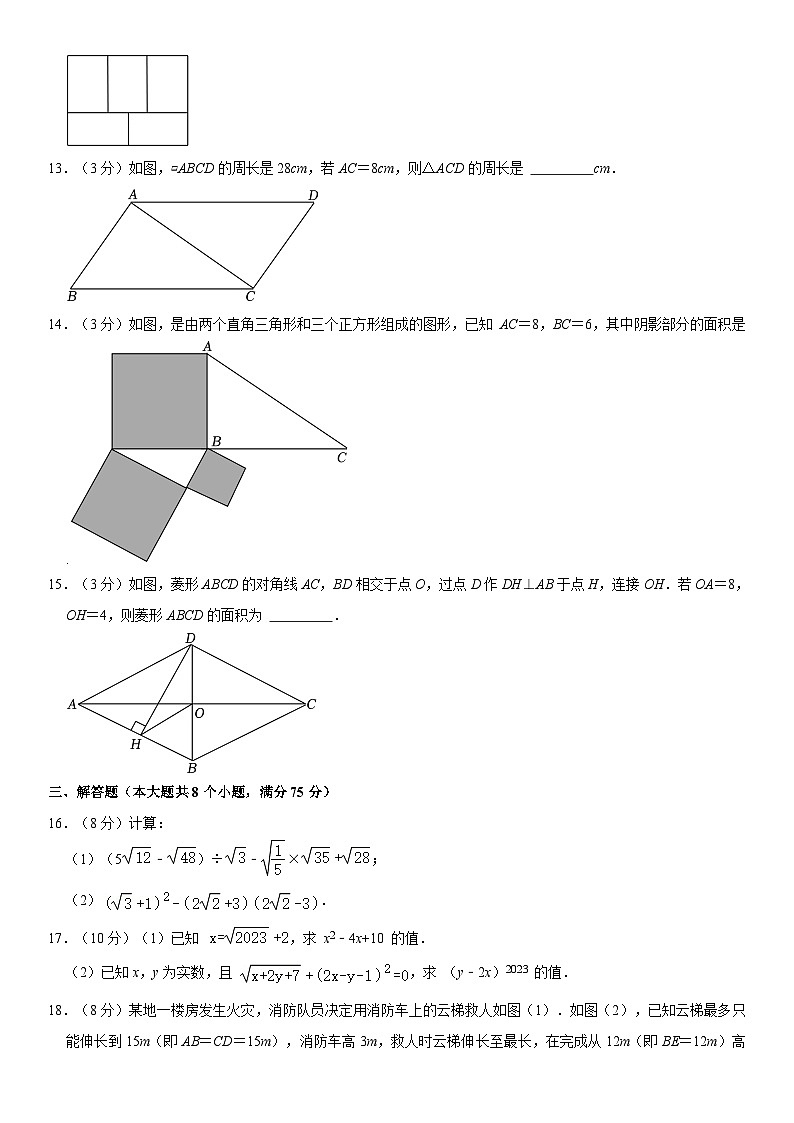
10．（3分）如图，O为正方形ABCD对角线AC的中点，△ACE为等边三角形．若AB＝4，则OE的长为（　　）

A． B． C． D．
、填空题（每小题3分，共15分）
11．（3分）若代数式有意义，则x的取值范围是 　 　．
12．（3分）如图，在数学课上，老师用5个完全相同的小长方形在无重叠的情况下拼成了一个大长方形，已知小长方形的长为，宽为，则这个大长方形的周长为 　 　．

13．（3分）如图，▱ABCD的周长是28cm，若AC＝8cm，则△ACD的周长是 　 　cm．

14．（3分）如图，是由两个直角三角形和三个正方形组成的图形，已知 AC＝8，BC＝6，其中阴影部分的面积是 　 　.
15．（3分）如图，菱形ABCD的对角线AC，BD相交于点O，过点D作DH⊥AB于点H，连接OH．若OA＝8，OH＝4，则菱形ABCD的面积为 　 　．

三、解答题（本大题共8个小题，满分75分）
16．（8分）计算：
（1）（5﹣）÷﹣×；
（2）．
17．（10分）（1）已知 ，求 x2﹣4x+10 的值．
（2）已知x，y为实数，且 ，求 （y﹣2x）2023 的值．
18．（8分）某地一楼房发生火灾，消防队员决定用消防车上的云梯救人如图（1）．如图（2），已知云梯最多只能伸长到15m（即AB＝CD＝15m），消防车高3m，救人时云梯伸长至最长，在完成从12m（即BE＝12m）高的B处救人后，还要从15m（即DE＝15m）高的D处救人，这时消防车从A处向着火的楼房靠近的距离AC为多少米？（延长AC交DE于点O，AO⊥DE，点B在DE上，OE的长即为消防车的高3m）．

19．（9分）如图，在四边形ABCD中，∠B＝90°，AB＝BC＝4，CD＝6，DA＝2．
（1）求∠DAB的度数；
（2）求四边形ABCD的面积．

20．（10分）如图，点E，A，C，F在同一直线上，ED∥BF，AE＝CF，∠EDA＝∠FBC．
求证：（1）△ADE≌△CBF；
（2）四边形ABCD是平行四边形．

21．（10分）在四边形ABCD中，AB∥CD，AC平分∠DAB，CE∥AD交AB于点E．
（1）求证：四边形AECD为菱形；
（2）若点E为AB的中点，AC＝8，AB＝3BC，求BC的长．

22．（10分）阅读下列材料，然后解决问题．
在进行二次根式的化简时，我们有时会遇到形如，，的式子，其实我们可以将其进一步化简：，＝，如上这种化简的步骤叫做“分母有理化”．
（1）化简＝　 　，＝　 　，＝　 　．
（2）化简：．
23．（10分）综合与实践：
在一次数学活动课上，老师带领学生对矩形纸片进行如下操作：
（1）探究一：
如图1，矩形纸片ABCD中，AD＞AB．如图2，点P在BC上，点Q在CD上，∠QPC＝45°，将纸片沿PQ翻折，使顶点C落在矩形ABCD内，对应点为 C'PC'的延长线交直线AD于点M，再将纸片的另一部分翻折，使顶点A落在直线 PC'上，对应点为A′，折痕为MN．猜想PQ，MN之间的位置关系为：　 　
（2）探究二：
如图3，将纸片任意翻折，折痕PQ（P在BC上，Q在CD上），使顶点C落在矩形ABCD内，对应点为 C'PC'的延长线交直线AD于点M，再将纸片的另一部分翻折，使顶点A落在直线 PC'上，对应点为 A'，折痕为MN．猜想PQ，MN之间的位置关系，并给出证明．
（3）探究三：
如图4，若∠QPC＝30°，BC＝12，当P为BC的三等分点时，直接写出C′M的值．

2022-2023学年河南省许昌市禹州市八年级（下）期中数学试卷
参考答案与试题解析
一、选择题（每小题3分，共30分）下列各小题均有四个答案，其中只有一个是正确的.
1．【分析】根据最简二次根式的定义对各选项进行判断．
【解答】解：A． 为最简二次根式，所以A选项符合题意；
B． ＝，则不是最简二次根，所以B选项不符合题意；
C． ＝，则不是最简二次根，所以C选项不符合题意；
D． ＝2，则不是最简二次根，所以D选项不符合题意；
故选：A．
2．【分析】根据勾股定理的逆定理，进行计算逐一判断即可解答．
【解答】解：∵（a+c）（a﹣c）＝b2，
∴a2﹣c2＝b2，
∴a2＝b2+c2，
∴△ABC是直角三角形，
∴∠A为直角，
故选：A．
3．【分析】直接利用二次根式的性质以及绝对值的性质分别化简，进而得出答案．
【解答】解：∵1＜a＜2，
∴
＝3﹣a+a﹣1
＝2．
故选：C．
4．【分析】根据二次根式的乘除法运算即可．
【解答】解：原式＝
＝
＝
＝
＝
＝，
故选：D．
5．【分析】分别写出各个命题的逆命题，根据对顶角相等、不等式的性质、直角三角形的概念、三角形全等的判定定理判断．
【解答】解：A、对顶角相等的逆命题是相等的角是对顶角，不成立，不符合题意；
B、若ac2＞bc2，则a＞b的逆命题是若a＞b，则ac2＞bc2，不成立，不符合题意；
C、直角三角形的两锐角互余的逆命题是有两个角互余的三角形是直角三角形，成立，符合题意；
D、全等三角形的对应角相等的逆命题是三个角对应相等的三角形全等，不成立，不符合题意；
故选：C．
6．【分析】先利用勾股定理求出AC，根据AC＝AM，求出OM，由此即可解决问题．
【解答】解：∵四边形ABCD是矩形，
∴∠ABC＝90°，
∵AB＝3，AD＝BC＝1，
∴，
∴AN＝AC＝，
∵点A表示﹣1，
∴OA＝1，
∴OM＝AM﹣OA＝﹣1，
∴点M表示点数为﹣1．
故选：A．
7．【分析】由平行四边形的判定方法分别对各个选项进行判断即可．
【解答】解：A、由数据可知，一组对边平行，另一组对边相等，不能判定为平行四边形，故选项A不符合题意；
B、由数据可知，一组对边平行且相等，能判定为平行四边形，故选项B符合题意；
C、由数据可知，只有一组对边平行，不能判定为平行四边形，故选项C不符合题意；
D、由数据可知，有三条边相等，不能判定为平行四边形，故选项D不符合题意；
故选：B．
8．【分析】根据三角形中位线定理求出EF，根据四边形的周长公式计算，得到答案．
【解答】解：∵E，F分别是边AB，AC的中点，AB＝12m，BC＝16m，AC＝14m，
∴EF是△ABC的中位线，BE＝AB＝6m，CF＝AC＝7m，
∴EF＝BC＝8m，
∴四边形花坛BCFE的周长＝BC+CF+EF+BE＝16+7+8+6＝37（m），
故选：C．
9．【分析】根据矩形，菱形的性质即可解答．
【解答】解：A、菱形和矩形的内角和都等于360°，故选项A不符合题意；
B、对角线互相平分是矩形、菱形都具有的性质，故选项B不符合题意；
C、菱形的对边平行且相等，矩形的对边平行且相等，故选项C不符合题意；
D、菱形每条对角线平分一组对角，矩形的对角线相等，不一定每条对角线平分一组对角，故选项D符合题意；
故选：D．
10．【分析】首先利用正方形的性质可以求出AC，然后利用等边三角形的性质可求出OE．
【解答】解：∵四边形ABCD为正方形，AB＝4，
∴AC＝4，
∵O为正方形ABCD对角线AC的中点，△ACE为等边三角形，
∴∠AOE＝90°，
∴AC＝AE＝4，AO＝2，
∴OE＝2×＝2．
故选：B．
、填空题（每小题3分，共15分）
11．【分析】根据二次根式中的被开方数是非负数、分母不为零列出不等式组，解不等式组得到答案．
【解答】解：由题意得：3﹣x≥0且x+1≠0，
解得：x≤3且x≠﹣1，
故答案为：x≤3且x≠﹣1．
12．【分析】大长方形的宽是小长方形的长和宽之和，大长方形的长是小长方形的长的2倍，是小长方形宽的3倍，
【解答】解：∵大长方形的宽＝3+2＝5，大长方形的长＝3×2＝6，
∴大长方形的周长＝（5+6）×2＝22，
故答案为：22．
13．【分析】由▱ABCD的周长是28cm，得出AD+AD＝14cm，再根据AC＝8cm，得出△ACD的周长是22cm．
【解答】解：∵▱ABCD的周长是28cm，
∴CD+AD＝14cm，
∵AC＝8cm，
∴△ACD的周长是14+8＝22（cm），
故答案为：22．
14．【分析】根据勾股定理求出AB2，再根据勾股定理计算即可．
【解答】解：在Rt△ABC中，AB2＝BE2＝AC2﹣BC2＝82﹣62＝28，
在Rt△BEH中，BE2＝EH2+BH2＝28，
∴阴影部分的面积＝正方形ABED的面积+正方形EHGF的面积+正方形的BHMN面积＝AB2+EH2+BH2＝2AB2＝2×28＝56．


故答案为：56．
15．【分析】由菱形的性质得OA＝OC＝8，OB＝OD，AC⊥BD，则AC＝12，再由直角三角形斜边上的中线性质求出BD的长度，然后由菱形的面积公式求解即可．
【解答】解：∵四边形ABCD是菱形，
∴OA＝OC＝8，OB＝OD，AC⊥BD，
∴AC＝16，
∵DH⊥AB，
∴∠BHD＝90°，
∴BD＝2OH＝2×4＝8，
∴菱形ABCD的面积＝AC•BD＝×16×8＝64，
故答案为：64．
三、解答题（本大题共8个小题，满分75分）
16．【分析】（1）先计算二次根式的乘除法，再算加减，即可解答；
（2）利用平方差公式，完全平方公式进行计算，即可解答．
【解答】解：（1）（5﹣）÷﹣×
＝5÷﹣÷﹣+2
＝5﹣﹣+2
＝10﹣4﹣+2
＝6+；
（2）
＝3+2+1﹣（8﹣9）
＝3+2+1+1
＝5+2．
17．【分析】（1）将 x2﹣4x+10可变为（x﹣2）2+6，再整体代入计算即可；
（2）根据算术平方根、偶次方的非负性，求出x、y的值，再代入计算即可．
【解答】解：（1）∵，即x﹣2＝，
∴x2﹣4x+10
＝（x﹣2）2+6
＝2023+6
＝2029；
（2）∵，而≥0，（2x﹣y﹣1）2≥0，
∴，
解得，
∴（y﹣2x）2023
＝（﹣3+2）2023
＝（﹣1）2023
＝﹣1．
18．【分析】在Rt△ABO中，根据勾股定理得到AO和OC，于是得到结论．
【解答】解：在Rt△ABO中，
∵AB＝15m，OB＝12﹣3＝9（m），
∴（m），
在Rt△COD中，
∵∠COD＝90°，CD＝15m，OD＝15﹣3＝12（m），
∴（m），
∴AC＝OA﹣OC＝3（m），
答：AC为3m．
19．【分析】（1）利用勾股定理可求AC，求出AC2+DA2＝CD2，由勾股定理的逆定理可证△ACD是直角三角形，再由∠DAB＝∠CAD+∠BAC即可得出结论；
（2）由三角形的面积公式即可得出结果．
【解答】解：（1）连接AC，
∵∠B＝90°，AB＝BC＝4，
∴AC＝＝＝4，
又∵CD＝6，DA＝2，
∴AC2+DA2＝CD2，
∴△ACD是直角三角形，∠CAD＝90°，
∵AB＝AC，
∴∠BAC＝45°，
∴∠DAB＝∠CAD+∠BAC＝90°+45°＝135°；
（2）四边形ABCD的面积＝△ABC的面积+△ACD的面积
＝×4×4+×2×4
＝8+4．

20．【分析】（1）由平行线的性质得∠E＝∠F，再由AAS证△ADE≌△CBF即可；
（2）由全等三角形的性质得AD＝CB，∠DAE＝∠BCF，再证AD∥CB，然后由平行四边形的判定即可得出结论．
【解答】证明：（1）∵ED∥BF，
∴∠E＝∠F，
在△ADE和△CBF中，
，
∴△ADE≌△CBF（AAS）；
（2）由（1）可知，△ADE≌△CBF，
∴AD＝CB，∠DAE＝∠BCF，
∴∠DAC＝∠BCA，
∴AD∥CB，
∴四边形ABCD是平行四边形．
21．【分析】（1）先证明四边形AECD是平行四边形，再证明AD＝CD即可；
（2）根据菱形的性质得到AE＝CE，求得CE＝，推出∠ACB＝90°，根据勾股定理即可得到结论．
【解答】（1）证明：∵AB∥CD，CE∥AD，
∴四边形AECD是平行四边形．
∵AC平分∠BAD，
∴∠DAC＝∠CAB．
∵AB∥CD，
∴∠CAB＝∠DCA，
∴∠DAC＝∠DCA，
∴AD＝CD，
∴四边形AECD是菱形；
（2）解：∵点E为AB的中点，
∴AE＝BE，
∵四边形AECD为菱形，
∴AE＝CE，
∴CE＝，
∴∠ACB＝90°，
∴AC2+BC2＝AB2，
∵AC＝8，AB＝3BC，
∴82+BC2＝（3BC）2，
∴BC＝2．
22．【分析】（1）利用例题的解题思路进行计算，即可解答；
（2）先进行分母有理化，然后再进行计算即可解答．
【解答】解：（1）＝＝，
＝＝，
＝＝＝﹣，
故答案为：；；﹣；
（2）
＝+++
＝+++
＝（﹣1+﹣+﹣+﹣）
＝．
23．【分析】（1）由矩形的性质可得AD∥BC，则∠AMP＝∠MPC，由折叠可知∠QPC＝∠QPC′＝45°，∠AMN＝∠A′MN，于是得到∠AMP＝∠MPC＝90°，进而得到∠AMN＝∠A′MN＝45°，由内错角相等，两直线平行即可证明；
（2）①由矩形的性质可得AD∥BC，则∠AMP＝∠MPC，由折叠可知∠AMN＝∠NMP＝，∠CPQ＝∠QPM＝，于是∠NMP＝∠QPM，由内错角相等，两直线平行即可证明；
②易通过ASA证明△AMN≌△CPQ，得到MN＝PQ，则可根据“对边平行且相等的四边形为平行四边形”来证明；
（3）分两种情况讨论：①当BP＝时，过点M作MG⊥BC于点G，则BP＝4，PC＝PC′＝8，MG＝AB＝6，易得∠MPG＝60°，于是可得PM＝＝12，则C′M＝PM﹣PC′；②当BP＝BC时，过点M作MG⊥BC的延长线于点G，则BP＝8，PC＝PC′＝4，MG＝AB＝，易得∠MPG＝60°，于是可得PM＝＝12，则C′M＝PM﹣PC′．
【解答】（1）解：结论：PQ∥MN．
理由：∵四边形ABCD为矩形，
∴AD∥BC，
∴∠AMP＝∠MPC，
根据折叠的性质可得，∠QPC＝∠QPC′＝45°，∠AMN＝∠A′MN，
∴∠AMP＝∠MPC＝90°，
∴∠AMN＝∠A′MN＝45°，
∴∠A′MN＝∠QPC′＝45°，
∴PQ∥MN；
故答案为：PQ∥MN；
（2）结论：PQ∥MN．
理由：∵四边形ABCD为矩形，
∴AD∥BC，
∴∠AMP＝∠MPC，
由折叠的性质可得，∠AMN＝∠NMP＝，∠CPQ＝∠QPM＝，
∴∠NMP＝∠QPM，
∴PQ∥MN；

（3）解：①当BP＝时，过点M作MG⊥BC于点G，如图，

∵AB＝6，BC＝12，
∴BP＝4，PC＝PC′＝8，MG＝AB＝6，
∵∠CPQ＝∠C′PQ＝30°，
∴∠MPG＝60°，
在Rt△PMG中，PM＝＝＝12，
∴C′M＝PM﹣PC′＝12﹣8＝4；
②当BP＝BC时，过点M作MG⊥BC的延长线于点G，如图，

∵AB＝6，BC＝12，
∴BP＝8，PC＝PC′＝4，MG＝AB＝6，
∵∠CPQ＝∠C′PQ＝30°，
∴∠MPG＝60°，
在Rt△PMG中，PM＝＝12，
∴C′M＝PM﹣PC′＝12﹣4＝8．
综上，C′M的值为8或4．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/9/2 5:31:58；用户：13776644732；邮箱：13776644732；学号：38246260