专题4.2 对数函数-2023-2024学年高一数学常考考点训练（北师大版2019必修第一册）

这是一份专题4.2 对数函数-2023-2024学年高一数学常考考点训练（北师大版2019必修第一册），文件包含专题42对数函数5类必考点北师大版2019必修第一册原卷版docx、专题42对数函数5类必考点北师大版2019必修第一册解析版docx等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。
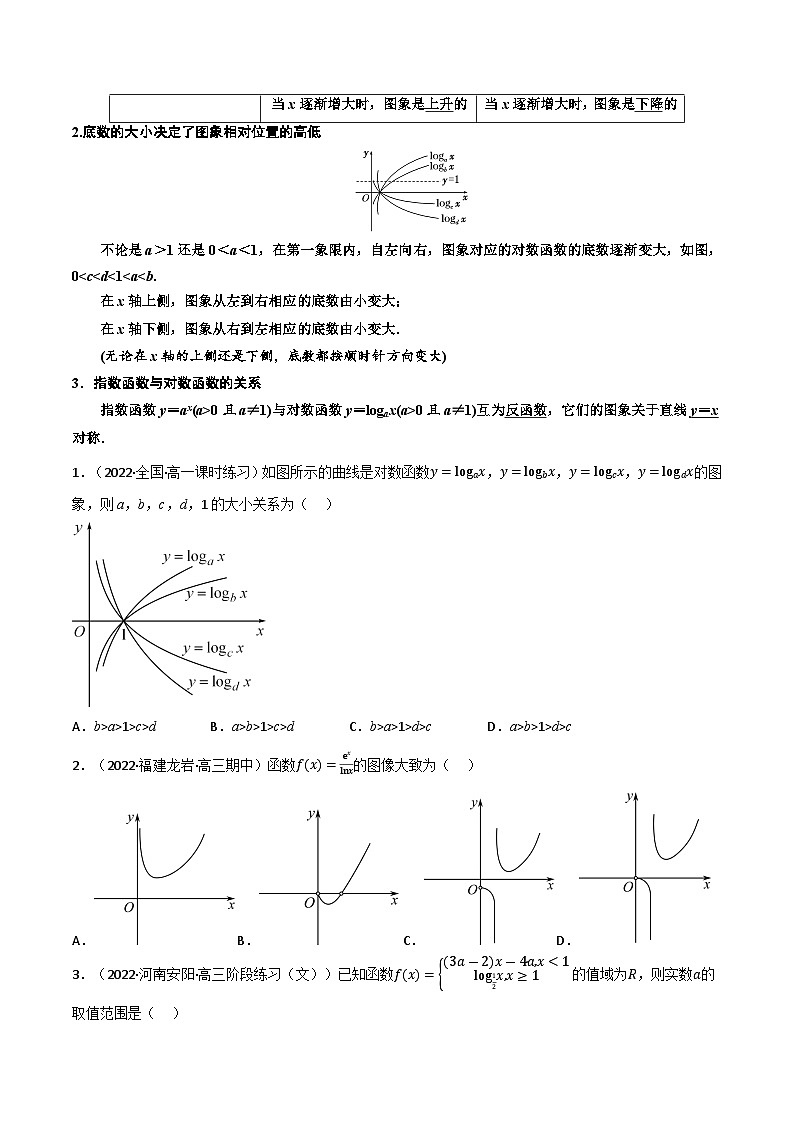
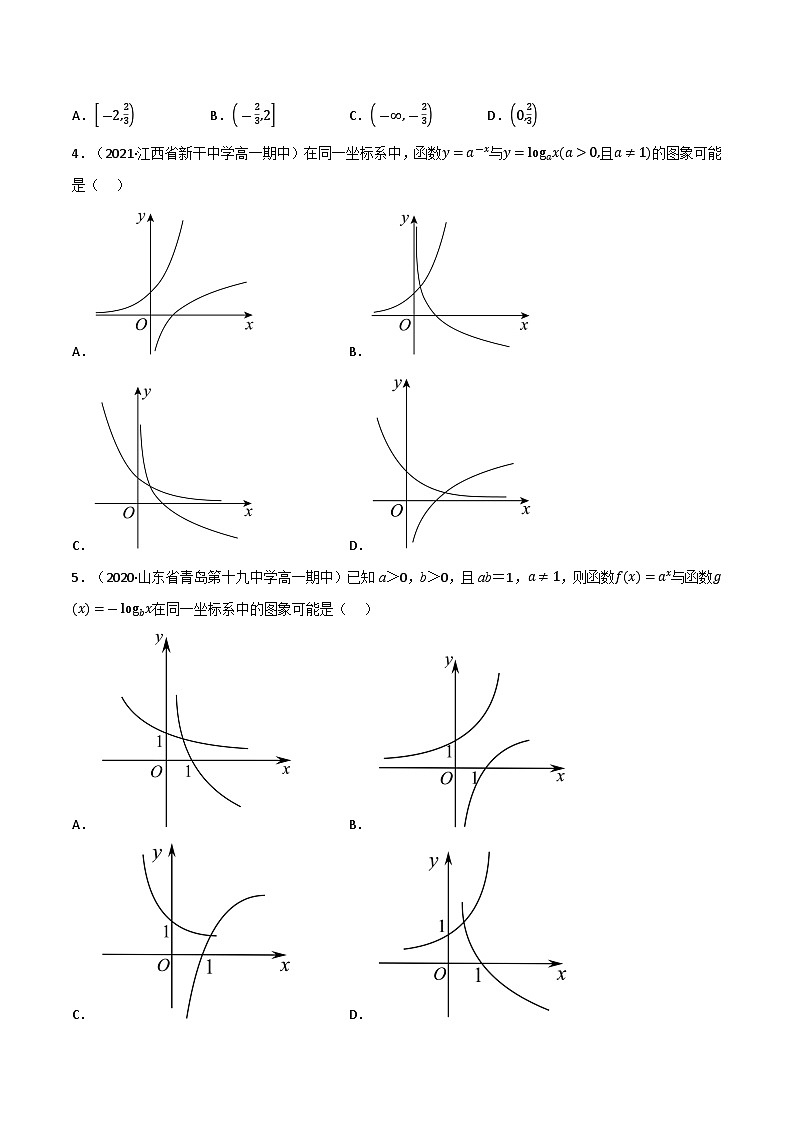
专题4.2 对数函数【考点1：对数函数的概念】【考点2：对数函数的图象】【考点3：对数函数的定义域与值域】【考点4：对数函数的单调性与最值】【考点5：对数函数的应用】【考点1：对数函数的概念】【知识点：对数函数的概念】形如y＝logax（a>0且）的函数为对数函数.1．（2022·全国·高一课时练习）下列函数是对数函数的是（    ）A． B． C． D．2．（2022·全国·高一课时练习）下列函数是对数函数的是(      )A．    B．    C．    D．3．（2023·全国·高三专题练习）若函数的图象过点，则（    ）A．3 B．1 C．-1 D．-34．（2022·全国·高一课时练习）已知为对数函数，，则______．5．（2022·北京市第十三中学高三开学考试）已知函数，且.则___________；___________. 【考点2：对数函数的图象】【知识点：对数函数的图象】1．对数函数的图象函数y＝logax，a>1y＝logax,0<a<1图象图象特征在y轴右侧，过定点(1,0)当x逐渐增大时，图象是上升的当x逐渐增大时，图象是下降的2.底数的大小决定了图象相对位置的高低不论是a＞1还是0＜a＜1，在第一象限内，自左向右，图象对应的对数函数的底数逐渐变大，如图，0<c<d<1<a<b.在x轴上侧，图象从左到右相应的底数由小变大；在x轴下侧，图象从右到左相应的底数由小变大．(无论在x轴的上侧还是下侧，底数都按顺时针方向变大)3．指数函数与对数函数的关系指数函数y＝ax(a>0且a≠1)与对数函数y＝logax(a>0且a≠1)互为反函数，它们的图象关于直线y＝x对称．1．（2022·全国·高一课时练习）如图所示的曲线是对数函数，，，的图象，则a，b，c，d，1的大小关系为（    ）A．b>a>1>c>d B．a>b>1>c>d C．b>a>1>d>c D．a>b>1>d>c2．（2022·福建龙岩·高三期中）函数的图像大致为（    ）A．B．C．D．3．（2022·河南安阳·高三阶段练习（文））已知函数的值域为，则实数的取值范围是（    ）A． B． C． D．4．（2021·江西省新干中学高一期中）在同一坐标系中，函数与且的图象可能是（    ）A． B．C． D．5．（2020·山东省青岛第十九中学高一期中）已知a＞0，b＞0，且ab＝1，，则函数与函数在同一坐标系中的图象可能是（    ）A． B．C． D．6．（2022·上海市大同中学高一期中）函数必过定点___________.7．（2021·上海海洋大学附属大团高级中学高三期中）若函数是函数（且）的反函数，则函数的图象一定经过定点________．8．（2007·全国·高考真题（文））如图，已知过原点O的直线与函数的图象交于A，B两点，分别过点A，B作y轴的平行线与函数的图象交于C，D两点．(1)证明O，C，D三点在同一条直线上；(2)当轴时，求A点的坐标．       【考点3：对数函数的定义域与值域】【知识点：对数函数的定义域与值域】函数y＝logax(a>0，且a≠1)a>10<a<1性质定义域(0，＋∞)值域R1．（2022·浙江·高一期中）函数的定义域为（    ）A． B．C． D．2．（2022·北京四中高三期中）函数的定义域是______.3．（2022·北京·高三阶段练习（文））函数的值域为______．4．（2023·全国·高三专题练习）已知函数的值域为，则实数的取值范围为________．5．（2021·天津·高一期末）若函数的值域是，则实数a的取值范围是_________．6．（2022·河南·高三阶段练习（文））已知（且），且.(1)求a的值及的定义域；(2)求在上的值域.     7．（2022·安徽省怀宁县第二中学高三阶段练习）已知函数．(1)若，求的取值范围；(2)当时， 求函数的值域．              【考点4：对数函数的单调性与最值】【知识点：对数函数的单调性与最值】函数y＝logax(a>0，且a≠1)a>10<a<1性质单调性在(0，＋∞)上是增函数在(0，＋∞)上是减函数函数值变化规律当x＝1时，y＝0当x>1时，y>0；当0<x<1时，y<0当x>1时，y<0；当0<x<1时，y>01．（2008·湖南·高考真题（文））下面不等式成立的是（    ）A． B．C． D．2．（2022·福建·宁德市民族中学高三期中）函数的单调递增区间是（    ）A． B． C． D．3．（2022·福建·厦门一中高一期中）已知函数，若实数a满足，则的取值范围是（    ）A． B． C． D．4．（2022·北京市第一六一中学高三期中）关于函数，下列说法错误的是（    ）A．定义域为 B．图象关于轴对称C．图象关于原点对称 D．在内单调递增5．（2022·湖北·宜昌英杰学校高二阶段练习）若，，，则下列a，b，c的大小关系表达正确的为（    ）A． B．C． D．6．（2022·重庆·高三阶段练习）已知且，函数有最小值，则的取值范围是___________.   7．（2022·湖北·郧阳中学高一阶段练习）已知函数，给出以下说法：①若函数的最小值为，则；②若函数的定义域为，则；③若函数的值域为，则或；④若，则函数的单调减区间为；⑤若函数在上单调递减，则．其中正确说法的个数为__________个．8．（2022·安徽·砀山中学高三阶段练习）已知函数，其中且．(1)求的定义域及其图象的对称轴方程；(2)若的最大值为2，求a的值．      9．（2022·广东·深圳中学高一期中）设且，函数的图象过点.(1)求的值及的定义域；(2)求在上的单调区间和最大值.         10．（2022·安徽·高三阶段练习）已知函数，且）．(1)若函数的图象与函数的图象关于直线对称，且点在函数的图象上，求实数的值；(2)已知函数，．若的最大值为8，求实数的值．        11．（2022·浙江大学附属中学高一期末）已知，函数(1)若函数过点，求此时函数的解析式；(2)设，若对任意，函数在区间上的最大值与最小值的差不超过1，求的取值范围.            12．（2022·河南·新密市第二高级中学高一阶段练习）已知函数(1)设函数是定义在上的奇函数，当时，，求函数的解析式；(2)已知集合①求集合；②当时，函数的最小值为，求实数的值．          【考点5：对数函数的应用】【知识点：对数函数的应用】1．（2022·广西北海·一模（理））大西洋鲑鱼每年都要逆流而上，游回到自己出生的淡水流域产卵．记鲑鱼的游速为v（单位：），鲑鱼的耗氧量的单位数为Q，研究发现．当时，鲑鱼的耗氧量的单位数为800．当时，鲑鱼的耗氧量的单位数为（    ）A．12800 B．24800 C．25600 D．512002．（2022·江苏江苏·高三阶段练习）每年3月3日是国际爱耳日，2022年的主题是“关爱听力健康，聆听精彩未来”．声强级是表示声强度相对大小，其值为（单位），定义，其中为声场中某点的声强度，其单位为m2（瓦/平方米） m2为基准值．如果飞机起飞时的声音是120，两人轻声交谈的声音是40，那么前者的声强度是后者的声强度的（    ）倍？A． B． C． D．3．（2022·北京市八一中学高三阶段练习）点声源在空间中传播时，衰减量与传播距离（单位：米）的关系式为（单位：），取，则从8米变化到40米时，衰减量的增加值约为（    ）A． B． C． D．4．（2022·浙江大学附属中学高一期中）声强级Li（单位：dB）为声强I（单位：）之间的关系是：，其中指的是人能听到的最低声强，对应的声强级称为闻阈．人能承受的最大声强为，对应的声强级为120dB，称为痛阈．某歌唱家唱歌时，声强级范围为[70，80]（单位：dB），下列选项中错误的是（    ）A．闻阈的声强级为0dBB．此歌唱家唱歌时的声强范围（单位：）C．如果声强变为原来的2倍，对应声强级也变为原来的2倍D．声强级增加10dB，则声强变为原来的10倍5．（2022·江苏常州·高一期中）声强级Li（单位：dB）与声强I（单位：）之间的关系是：，其中指的是人能听到的最低声强，对应的声强级称为闻阈．人能承受的最大声强为，对应的声强级为120dB，称为痛阈．某歌唱家唱歌时，声强级范围为（单位：dB）．下列选项中正确的是（    ）A．闻阈的声强为 B．声强级增加10dB，则声强变为原来的2倍C．此歌唱家唱歌时的声强范围（单位：dB）D．如果声强变为原来的10倍，对应声强级增加10dB6．（2022·上海市进才中学高三阶段练习）学校鼓励学生课余时间积极参加体育锻炼，现需要制定一个课余锻炼考核评分制度，建立一个每天得分y与当天锻炼时间x（单位：分钟）的函数关系，要求如下：（1）函数的图象接近图示；（2）每天运动时间为0分钟时，当天得分为0分；（3）每天运动时间为30分钟时，当天得分为3分；（4）每天最多得分不超过6分.现有以下三个函数模型供选择：①；②；③.(1)请你从中选择一个合适的函数模型并说明理由；(2)根据你对（1）的判断以及所给信息完善你的模型并给出函数的解析式；(3)已知学校要求每天的分数不少于4.5分，求每天至少运动多少分钟（结果保留整数）.    7．（2022·北京朝阳·高三阶段练习）2022年6月5日神舟十四号载人飞船在长征二号F遥十四运载火箭的托举下点火升空，成功进入预定轨道．我国在航天领域取得的巨大成就，得益于我国先进的运载火箭技术．根据火箭理想速度公式，可以计算理想状态下火箭的最大速度v（单位：），其中（单位：）是喷流相对速度，m（单位：kg）是火箭（除推进剂外）的质量，M（单位：kg）是推进剂与火箭质量的总和，应称为总质比．己知A型火箭喷流相对速度为，根据以上信息：（1）当总质比为50时，A型火箭的最大速度为___________；（2）若经过材料更新和技术改进后，A型火箭的喷流相对速度提高到原来的2倍，总质比变为原来的，若要使火箭的最大速度至少增加，则在材料更新和技术改进前总质比的最小值为___________．（所有结果保留整数，参考数据：）