2023届四川省遂宁市射洪中学校高三下学期开学考试数学（文）试题含答案

这是一份2023届四川省遂宁市射洪中学校高三下学期开学考试数学（文）试题含答案，共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
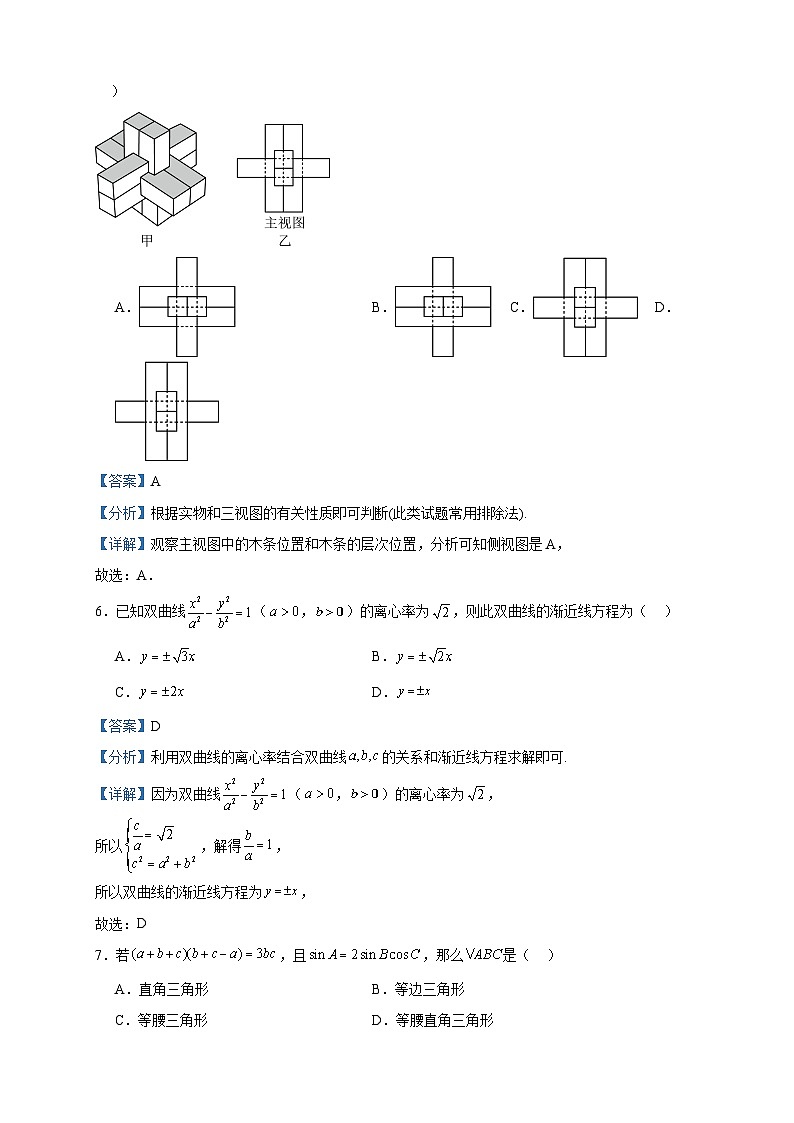
2023届四川省遂宁市射洪中学校高三下学期开学考试数学（文）试题 一、单选题1．已知集合，，若，则（    ）A．1 B．2 C．3 D．4【答案】B【分析】利用求出，进而求出.【详解】因为，所以，所以，，即，所以.故选B.2．已知等比数列，则（    ）A． B． C． D．【答案】A【分析】根据等比数列的下标性质进行求解即可.【详解】因为数列是等比数列。所以，故选：A3．若满足，则的最大值为（    ）A．1 B．3 C．5 D．9【答案】B【分析】作出不等式组所表示的可行域，利用目标函数的几何意义，找出目标函数取得最大值时的最优解，代入目标函数计算即可．【详解】出不等式组所表示的可行域如下图所示，令，联立，得，则点，平移直线，由图象可知，当直线经过可行域的顶点时，该直线在y轴上的截距最大，此时取得最大值，即．故选：B．4．已知函数，则（    ）A． B．为奇函数C．在上单调递增 D．的图象关于点对称【答案】D【分析】得，再代入求判断A;由函数定义域即可判断求B;由图象平移可判断的在区间的单调性和对称中心，从而判断C、D【详解】因为，则，故A错误；由解析式知定义域为，显然不关于原点对称，不是奇函数，故B错误；的图象可看作是由反比例函数的图象向右移动1个单位长度得到，且在上单调递减，且关于对称，故在上递减且关于对称，故C错误，D正确，故选：D5．榫卯，是一种中国传统建筑、家具及其他器械的主要结构方式，是在两个构件上采用凹凸部位相结合的一种连接方式．春秋时期著名的工匠鲁班运用榫卯结构制作出了鲁班锁，且鲁班锁可拆解，但是要将它们拼接起来则需要较高的空间思维能力和足够的耐心．如图甲，六通鲁班锁是由六块长度大小一样，中间各有着不同镂空的长条形木块组装而成．其主视图如图乙所示，则其侧视图为（    ）A． B． C． D．【答案】A【分析】根据实物和三视图的有关性质即可判断(此类试题常用排除法).【详解】观察主视图中的木条位置和木条的层次位置，分析可知侧视图是A，故选：A．6．已知双曲线（，）的离心率为，则此双曲线的渐近线方程为（    ）A． B．C． D．【答案】D【分析】利用双曲线的离心率结合双曲线的关系和渐近线方程求解即可.【详解】因为双曲线（，）的离心率为，所以，解得，所以双曲线的渐近线方程为，故选：D7．若，且，那么是（    ）A．直角三角形 B．等边三角形C．等腰三角形 D．等腰直角三角形【答案】B【分析】由给定边的关系式结合余弦定理求出角A，再由正弦定理角化边，结合边的关系式可得c=b即可推理作答. 【详解】由，得，化简得，所以，由余弦定理得，因为，所以，因为，所以，由正余弦定理角化边得，化简得，所以，即为等边三角形．故选：B8．为响应“健康中国2030”的全民健身号召，某校高一年级举办了学生篮球比赛，甲､乙两位同学在6场比赛中的得分茎叶图如图所示，下列结论正确的是（    ）A．甲得分的极差比乙得分的极差小B．甲得分的平均数比乙得分的平均数小C．甲得分的方差比乙得分的方差大D．甲得分的分位数比乙得分的分位数大【答案】C【分析】根据茎叶图求出甲，乙两位同学得分的极差，平均分，方差，百分位数即可解决.【详解】由题知，甲同学6场比赛得分分别为14,16,23,27,32,38，极差为，平均数，方差，因为，所以得分的25%分位数为16，乙同学6场比赛得分分别为13,22,24,26,28,37，极差为，平均数，方差，因为，所以得分的25%分位数为22，所以ABD错误；故选：C9．若函数在处有极大值，则实数的值为（    ）A． B．或 C． D．【答案】D【分析】由题意解得的值，再根据极大值、极小值的概念验证即可.【详解】求导得，则由题意得或，代入检验当时，，令或，，则时，取得极小值，不符合题意舍去；当时，，令或，，则时，取得极大值，符合题意.故选：D10．已知三棱柱的6个顶点都在球的球面上，若，，，，则球的表面积为（    ）A． B． C． D．【答案】B【分析】由于直三棱柱的底面是直角三角形，所以可以把此三棱柱补成直四棱柱，其体对角线就是外接球的直径，求得球的半径，利用球的表面积公式，即可求解．【详解】方法一：由于直三棱柱的底面是直角三角形，所以可以把此三棱柱补成直四棱柱，其体对角线就是外接球的直径，所以半径，由球的表面积公式得，故选：B．方法二：如图，取的中点分别为，根据题意，它们分别是的外心，因为，所以四边形是平行四边形，所以，而底面ABC，所以底面ABC，取的中点O，于是点O为该直三棱柱外接球的球心．连接OB，容易求得，则外接球半径，于是外接球的表面积为，故选：B．11．关于某校运动会米决赛前三名选手甲、乙、丙有如下命题：“甲得第一”为命题；“乙得第二”为命题；“丙得第三”为命题.若为真命题，为假命题，为假命题，则下列说法一定正确的为（    ）A．甲不是第一 B．乙不是第二C．丙不是第三 D．根据题设能确定甲、乙、丙的顺序【答案】C【分析】由为真命题，为假命题，确定，一真一假，再结合命题内容，进行辨析即可.【详解】∵为真命题，为假命题，∴命题与命题中，恰有一个为真命题，另一个为假命题；（1）若命题：“甲得第一”为真命题，命题：“乙得第二”为假命题，则甲得第一，乙未得第二，∴乙得第三，∴命题：“丙得第三”为假命题，此时为假命题满足题意，前三名的顺序为：甲得第一，丙得第二，乙得第三；（2）若命题：“甲得第一”为假命题，命题：“乙得第二”为真命题，则乙得第二，甲未得第一，∴甲得第三，∴命题：“丙得第三”为假命题，此时为假命题满足题意，前三名的顺序为：丙得第一，乙得第二，甲得第三.对于A，第（1）种情况中，甲得第一，满足题意，故选项A说法不正确；对于B，第（2）种情况中，乙得第二，满足题意，故选项B说法不正确；对于C，（1）、（2）两种情况中，丙均不是第三，故选项C说法正确；对于D，（1）、（2）两种情况中，存在两种不同顺序，故根据题设不能确定甲、乙、丙的顺序，故选项D说法不正确.故选：C.12．已知函数的最小正周期为2，且函数图像过点，若在区间内有4个零点，则的取值范围为（    ）A． B．C． D．【答案】A【分析】根据最小正周期求出，根据函数图像过点求出的值，再根据复合函数画出外层函数的图像，求出右端点的范围.【详解】的最小正周期为2又函数过点，即，又又，若在区间内有4个零点，如图，则满足所以故选：A 二、填空题13．复数（其中是虚数单位），则  ．【答案】【分析】根据复数的除法运算和共轭复数定义求解.【详解】，.故答案为: .14．已知直线与圆相切，则实数          ．【答案】【分析】通过圆心到直线的距离等于半径列方程求解即可.【详解】由题意得，圆的圆心坐标为，半径为，则圆心到直线的距离，又，所以解得，故答案为：15．在中，分别为的中点，则          .【答案】－4【分析】由向量的线性运算得，，然后计算数量积可得．【详解】由已知，，．故答案为：．16．已知抛物线的焦点为，过点的直线交于两个不同点，则下列结论正确的是      .①若点，则的最小值是3②的最小值是2③若，则直线的斜率为④过点分别作抛物线的切线，设两切线的交点为，则点的横坐标为【答案】①③④【分析】过点分别作准线的垂线，垂足分别为，进而根据抛物线的定义判断①；根据判断②；设直线的方程为，，进而联立方程，结合韦达定理，根据解方程即可得判断③；根据直线与曲线的位置关系得过点，分别与抛物线相切的直线方程为，，进而联立方程解得可判断④.【详解】由题知，，准线方程为，对于①选项，如图，过点分别作准线的垂线，垂足分别为，故，故①正确；对于②，设，故，故②错误；对于③，当直线的斜率不存在时，，不成立；故直线的斜率存在，设方程为，与抛物线方程联立，得，所以，因为，所以，即，解得，故③正确；对于④，设过点与抛物线相切的直线方程为，与抛物线方程联立得，所以，整理得，所以，故即为，整理得，同理得过点与抛物线相切的直线方程为，所以，联立方程，解方程得，因为，所以，所以，即点的横坐标为，故④正确.故选：①③④【点睛】圆锥曲线中最值或范围问题的常见解法：（1）几何法，若题目的条件和结论能明显体现几何特征和意义，则考虑利用几何法来解决；（2）代数法，若题目的条件和结论能体现某种明确的函数关系，则可首先建立目标函数，再求这个函数的最值或范围． 三、解答题17．某工厂为了检验某产品的质量，随机抽取100件产品，测量其某一质量指数，根据所得数据，按分成5组，得到如图所示的频率分布直方图.(1)估计该产品这一质量指数的中位数；(2)若采用分层抽样的方法从这一质量指数在和内的该产品中抽取6件，再从这6件产品中随机抽取2件，求这2件产品不是取自同一组的概率.【答案】(1)15.(2). 【分析】（1）根据频率分布直方图，利用中位数的含义，列式计算，可得答案;（2）确定质量指数在和内产品件数，即可确定采用分层抽样的方法，从这6件产品中随机抽取2件，每组里的抽取的件数，列出所有情况，根据古典概型的概率公式，计算可得答案.【详解】（1）因为，，所以该产品这一质量指数的中位数在内，设该产品这一质量指数的中位数为，则，解得；（2）由频率分布直方图可得，即在和的产品分别由件，采用分层抽样的方法抽取的6件产品中这一质量指数在内的有4件，记为，这一质量指数在内的有2件，记为，从这6件产品中随机抽取2件的情况有，共15种；其中符合条件的情况有，共8种，故所求概率.18．已知数列是公比为正数的等比数列，且，.(1)求数列的通项公式；(2)若，求数列的前项和.【答案】(1)(2) 【分析】（1）利用等比数列通项公式可构造方程求得公比，进而得到；（2）由（1）可得，采用错位相减法可求得.【详解】（1）设等比数列的公比为，由得：，，解得：（舍）或，.（2）由（1）得：，，，，，.19．如图，在四棱锥中，底面为直角梯形，，平面底面分别为的中点..(1)求证：直线平面；(2)求三棱锥的体积.【答案】(1)证明见解析(2) 【分析】（1）在梯形中证明是矩形，得，然后由面面垂直的性质定理得与平面垂直，从而有，由此得证线面垂直．（2）由棱锥的体积公式转化计算：．【详解】（1）因为为的中点，，所以，又因为，所以四边形为平行四边形，因为，所以平行四边形是矩形，所以，因为，所以，又因为平面平面，平面平面平面，所以平面，因为平面，所以，又因为平面，所以平面.（2）因为，所以，由平面为中点，所以点到平面的距离等于，所以.20．已知函数.(1)讨论函数的单调性；(2)若函数有两个不同的零点，求的范围.【答案】(1)答案见解析；(2). 【分析】（1）求导得，再根据分类结论即可；（2）分离参数得，令，借助的图象单调性分析即得的范围.【详解】（1）函数的定义域为，，当时，恒成立，故函数在上单调递减；当时，令，得，令，得，故函数在上单调递减，在上单调递增.（2）函数在上有两个不同的零点，等价于方程在上有两个不等实根，即有两个解，令，，则，令，得，令，得，函数在上单调递增，在上单调递减，，时，，当时，，所以函数的图象大致如下：，的范围是.21．已知椭圆的短轴顶点为，短轴长是4，离心率是，直线与椭圆C交于两点，其中.(1)求椭圆C的方程；(2)若（其中O为坐标原点），求k：(3)证明：是定值.【答案】(1)(2)(3)证明见解析 【分析】（1）由短轴长及离心率求得参数a、b即可；（2）由分析得，即，联立直线方程与椭圆方程结合韦达定理可解得k；（3）直接由斜率公式化简求值即可.【详解】（1）短轴长，离心率是，∴椭圆C的方程为.（2）直线l交y轴于，因为，则，所以，联立直线方程与椭圆方程得，由得或，由韦达定理得，把代入上式得①，②，得，解得，符合或，所以.（3）证明：由韦达定理得22．在直角坐标系xOy中，直线l的参数方程为（t为参数，）.以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为.(1)求曲线C的直角坐标方程和当时，直线l的普通力程；(2)若直线l与曲线C交于A，B两点，且与x轴交于点F，，求直线l的倾斜角.【答案】(1)，(2)或 【分析】(1)将，代入曲线C的极坐标方程化简即可得到曲线C的直角坐标方程，将代入直线l的参数方程为，消参即可求解；(2)将直线l的参数方程代入抛物线方程化为关于的方程，然后结合的几何意义和题干条件即可求解.【详解】（1）由得，，将，，代入得.当时，，消去t，得.∴曲线C的直角坐标方程为，直线l的普通方程为.（2）设A，B对应的参数分别为，，将代入得，，∴，，∴，异号，∴，∴，解得或.∵，∴或，∴直线l的倾斜角为或.23．已知函数，.(1)当时，解不等式；(2)若存在实数，使得不等式，求实数的取值范围.【答案】(1)(2) 【分析】（1）分类讨论求解不等式组即可得到答案.（2）首先将题意转化为存在实数，使得不等式有解，再利用绝对值三角不等式求解即可.【详解】（1）由题知：，，，，综上：所求不等式解集为.（2）存在实数，使得不等式，即存在实数，使得不等式有解，因为时取等号，所以，解得，即.