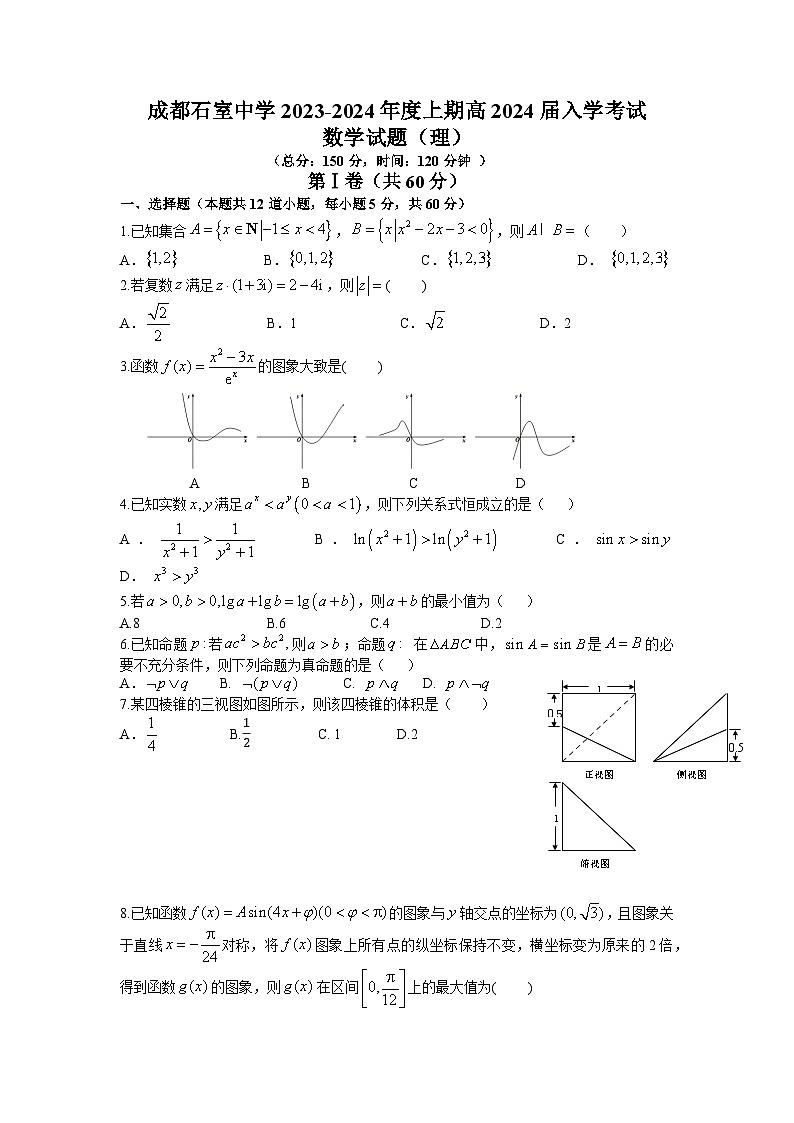
四川省成都市石室中学2023-2024学年高三上学期开学考试理科数学试题

这是一份四川省成都市石室中学2023-2024学年高三上学期开学考试理科数学试题，文件包含理科docx、理科答案docx等2份试卷配套教学资源，其中试卷共9页， 欢迎下载使用。
成都石室中学2023-2024年度上期高2024届入学考试数学试题（理 ）参考答案 一、       选择题题号123456789101112答案BCADCDACBACB二、       填空题13. ;    14. ;   15. ;  16. . 三、       解答题17．解：（1），又因为，所以是首项为2，公比为2的等比数列. ．．．．．．．．．．．．．5分（2）     满足上式.    . ．．．．．．．．．．．．．12分18．解：（1）因为平面平面，且平面平面，平面，，所以平面，所以．因为，，，所以，故． 又，所以平面．因为平面，所以，平面平面．      (6分)（2）在线段上取点，使，则，因为平面平面，且平面平面，平面，所以平面．              所以，可以建立如图所示空间直角坐标系，其中轴． 则，，，，所以，，．      设平面的法向量为，则即令得，，所以平面的一个法向量为．(9分)设平面的法向量为，则即令得，，所以平面的一个法向量为．        ，(11分)所以平面与平面所成的锐二面角的余弦值为．    (12分)19．解： （1）由 ，得，设中位数为，由 ，解得，由频率分布直方图可知众数为65. ．．．．．3分（2）从这1000人问卷调查得到的平均值为 因为由于得分服从正态分布，所以 .．．．．．．．．．．．．．7分（3）设得分不低于分的概率为，则，的取值为10，20，30，40，， ，， ，所以的分布列为：所以.．．．．．．．．．．．．．12分 20．解：（1）依题意得，则，.于是，从而. 又，解得所以椭圆的方程为. ．．．．．．．．．．．．．3分（2）如图，设直线交椭圆于另一点，直线交椭圆于另一点，由，故，由椭圆对称性，，且四边形为平行四边形. ．．．．．．．．．．．．．5分由题意直线的斜率不为0，设直线：，由，消去整理得，设，，则，，由（*）带入上式，解得：故，故的斜率为1. ．．．．．．．．．．．．．8分由，消去整理得，由得.所以，与间的距离（即点到的距离），故，令，则，所以四边形的面积的取值范围为. ．．．．．．．．．．．．．12分21．解：（1）考虑函数，易知在上单调递增，且，．因此有且只有使得，即的图象与直线有且只有一个公共点，且该公共点的横坐标为．   …………3分（2）．设是的图象上一点，则该点处的切线为，整理得．令，解得或．因此与与函数的图象相切．因此所求实数的值为或． …………7分（3）设，则．设，则．当时，；当时，．因此在上单调递增，在上单调递减．从而在上单调递增，上单调递减．注意到，故当时，当时，因此在上单调递减，在上单调递增．所以当时，．另一方面，注意到，故必然存在，使得，且当时，当时．因此在上单调递减，在上单调递增．显然，而．因此当时，．综上可知当时，即，当且仅当时等号成立．由于，故当，即时，，当且仅当，即时等号成立．因此，当且仅当时等号成立．因此的最大值为． …………12分 22．解：（1），故，；               ……5分（2）曲线，直线，分别代入，得，，由知，即，即，故即.                                              ……10分