2022-2023学年四川省成都市简阳市阳安中学高二下学期5月月考数学（文）试题含答案

这是一份2022-2023学年四川省成都市简阳市阳安中学高二下学期5月月考数学（文）试题含答案，共16页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
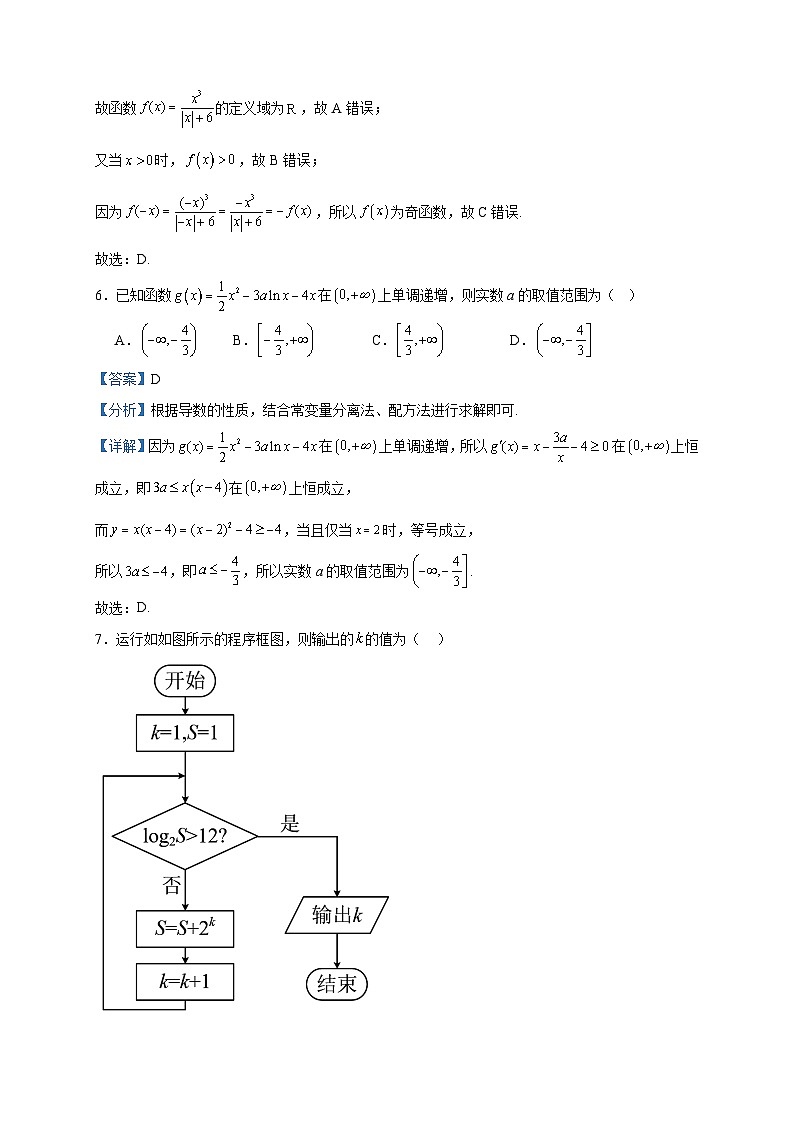
2022-2023学年四川省成都市简阳市阳安中学高二下学期5月月考数学（文）试题 一、单选题1．已知集合，则（    ）A． B． C． D．【答案】C【分析】根据交集的概念可求出结果.【详解】由已知得，所以.故选：C .2．若，则复数在复平面内对应的点在（    ）A．第一象限 B．第二象限 C．第三象限 D．第四象限【答案】A【分析】由复数除法运算法则，求出，即可求解.【详解】， 所以复数在复平面内对应的点在第一象限.故选：A.3．某市教体局对全市高一年级的学生身高进行抽样调查，随机抽取了100名学生，他们的身高都处在A，B，C，D，E五个层次内，根据抽样结果得到统计图表，则样本中B层人数是（    ）A．12 B．24 C．32 D．36【答案】D【分析】分别通过条形图和扇形图得出女生和男生的人数，最后相加即可.【详解】女生在B层次人数为24，而女生总人数为：9+24++15+9+3=60人，故男生人数为100-60=40人，在B层次人数为40×30%=12，所以在B层一共36人.故选：D.4．已知圆：，求的最小值（    ）．A． B． C． D．【答案】B【分析】设，问题转化为直线与圆有公共点，利用圆心到直线距离求解即可.【详解】设，则，则圆心到直线的距离，解得，即的最小值为，故选：B5．函数的大致图象为（    ）A． B．C． D．【答案】D【分析】由题可得函数定义域，函数的奇偶性及其在时的函数值符号，结合排除法即得.【详解】对任意的，，故函数的定义域为，故A错误；又当时，，故B错误；因为，所以为奇函数，故C错误.故选：D.6．已知函数在上单调递增，则实数a的取值范围为（   ）A． B． C． D．【答案】D【分析】根据导数的性质，结合常变量分离法、配方法进行求解即可.【详解】因为在上单调递增，所以在上恒成立，即在上恒成立，而，当且仅当时，等号成立，所以，即，所以实数a的取值范围为.故选：D.7．运行如如图所示的程序框图，则输出的的值为（    ）A． B． C． D．【答案】C【分析】由算法框图可知，是首项为，公比为的等比数列的前项和，表示出，在根据对数的性质计算可得；【详解】解：由算法框图可知，是首项为，公比为的等比数列的前项和，即，∵，，所以，故选：C.8．已知函数，则下列结论正确的是（    ）A．有两个零点 B．点是曲线的对称中心C．有两个极值 D．直线是曲线的切线【答案】C【分析】AC选项，求定义域，求导，得到函数单调性和极值情况，并得到的零点情况，判断AC；B选项，计算，故点不是曲线的对称中心；D选项，设出切点，根据导函数的几何意义得到切点横坐标，进而得到切点坐标和切线方程，判断D错误.【详解】AC选项，定义域为R，，当或1时，，令，解得，令，解得或，故在上单调递减，在上单调递增，故是的极大值点，1是的极小值点，故有两个极值，C正确；又，，当时，，当时，，故有3个零点，A错误；，故点不是曲线的对称中心，B错误；D选项，设是函数的切点，，令，解得，又，则函数在处的切线方程为，即是曲线的切线，D错误.故选：C9．已知，则（    ）A． B． C． D．【答案】D【分析】根据指数函数的单调性判断都大于1，利用，即可判断大小，根据对数函数性质可判断c的范围，即得答案.【详解】因为是R上的增函数，故,又，所以，而为单调减函数，故，故，故选：D10．一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的外接球的表面积为（    ）．A． B． C． D．【答案】A【分析】由三视图确定几何体的形状特征，进而确定外接球的球心位置，求得半径，进而计算可得.【详解】由已知几何体的正视图是一个正三角形，侧视图和俯视图均为三角形，可得该几何体有一个侧面PAC垂直于底面，高为，底面是一个等腰直角三角形的三棱锥，如图.因为，所以是的外心，则这个几何体的外接球的球心O在高线PD上，且是等边三角形PAC的中心，这个几何体的外接球的半径R＝.则这个几何体的外接球的表面积为故选：A.11．在平面直角坐标系中，圆的方程为，若直线上存在一点，使过点所作的圆的两条切线相互垂直，则实数的值不可能是（    ）A． B． C． D．【答案】B【分析】首先将圆的方程化为标准式，即可得到圆心坐标，依题意、及两切点构成正方形且，只需圆心到直线的距离小于等于，即可得到不等式，求出的取值范围，即可判断.【详解】由，得，则圆心，半径，因为过点所作的圆的两条切线相互垂直，所以、及两切点构成边长为的正方形，且对角线，又在直线上，则圆心到直线的距离，解得或，即，根据选项，满足条件的为B．故选：B．12．已知，分别是双曲线的左、右焦点，直线l经过且与C左支交于P，Q两点，P在以为直径的圆上，，则C的离心率是（    ）A． B． C． D．【答案】A【分析】根据P在以为直径的圆上，得到，设，，得到，由双曲线定义得到，求出，由勾股定理求出，从而求出离心率.【详解】不妨设，，因为P在以为直径的圆上，所以，即，则．因为Q在C的左支上，所以，即，解得，则．因为，所以，即，故，故．故选：A 二、填空题13．某产品的宣传费用x(万元)与销售额y(万元)的统计数据如下表所示：宣传费用x(万元)2345销售额y(万元)24304250根据上表可得回归方程，则宣传费用为6万元时，销售额约为           万元.【答案】59【分析】先求得样本点，代入回归方程，求得a，再将代入求解.【详解】，因为回归方程过点，所以，解得，即，当时，，故答案为：5914．若圆：与圆：外切，则实数      ．【答案】【分析】根据两圆外切列方程，从而求得的值.【详解】圆的圆心为，半径为.圆的圆心为，半径为.由于两圆外切，所以，得.故解得.故答案为： .15．设是定义在上的函数，其导函数为，若，，则不等式的解集为        ．【答案】【分析】构造函数，利用导数判断函数的单调性，进而得解.【详解】设，则，因为，所以，即是上的减函数，又，故可化为，即，所以，所以所求不等式解集为．故答案为：．16．设椭圆与双曲线的公共焦点为，将的离心率记为，点A是在第一象限的公共点，若点A关于的一条渐近线的对称点为，则        ．【答案】2【分析】由双曲线以及椭圆的定义可得，由曲线的一条渐近线是线段的中垂线可知，由勾股定理化简可得，由离心率概念可得结果.【详解】由题意可得焦距为，椭圆的长轴长为，双曲线的实轴长为，则由双曲线的定义可得，由椭圆的定义可得，所以，因为点A关于的一条渐近线的对称点为，所以双曲线的一条渐近线是线段的中垂线，所以，所以，所以，即，所以，所以，故答案为：2.【点睛】关键点点睛：通过点A关于的一条渐近线的对称点为，得到. 三、解答题17．已知函数．(1)求曲线在点处的切线方程．(2)求在区间上的最大值和最小值．【答案】(1)(2)最大值为，最小值为 【分析】（1）求导，利用导数的几何意义可求得切线方程；（2）利用导数确定函数在区间上的单调性，进而可得最值.【详解】（1）由已知，则，所以曲线在点处的切线方程为，即；（2）令，得或，令，得，所以在上单调递减，在上单调递增，又，，，所以在区间上的最大值为，最小值为.18．某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在内，发布成绩使用等级制，各等级划分标准见下表.百分制85分及以上70分到84分60分到69分60分以下等级ABCD规定：A，B，C三级为合格等级，D为不合格等级.为了解该校高三年级学生身体素质情况，从中抽取了n名学生的原始成绩作为样本进行统计.按照，，，，的分组作出频率分布直方图如图1所示，样本中分数在80分及以上的所有数据的茎叶图如图2所示（1）根据频率分布直方图，求成绩的中位数（精确到0.1）；（2）在选取的样本中，从A，D两个等级的学生中随机抽取2名学生进行调研，求至少有一名学生是A等级的概率.【答案】（1）中位数为；（2）.【分析】（1）根据频率分布直方图，计算成绩的中位数即可；（2）由茎叶图中的数据，利用列举法求出基本事件数，计算所求的概率值．【详解】解：（1）根据频率分布直方图，所以由，所以中位数位于内，所以中位数为；（2）由茎叶图知，等级的学生有3人，等级的学生有人，记等级的学生为、、，等级的学生为、、、、，从这8人中随机抽取2人，基本事件是：、、、、、、、、、、、、、、、、、、、、、、、、、、、共28个；至少有一名是等级的基本事件是：概率．、、、、、、、、、、、、、、、、、共18个；故所求的概率为．【点睛】本题考查了频率分布直方图的应用问题，也考查了列举法求古典概型的概率问题，属于基础题．19．如图，在四棱锥中，底面ABCD是矩形，M是PD的中点，，，，，.(1)证明：平面ABCD；(2)求点到平面的距离.【答案】(1)证明见解析(2) 【分析】（1）由勾股定理得到，，再利用直线与平面的垂直判定定理即可得证；（2）易证平面，又，可知平面，根据，利用等体积法即可求解.【详解】（1）证明：在矩形中，，，可得， 所以，即，连接，又点是的中点，，可得，所以，即. 又，所以平面.（2）因为，所以平面.又，所以平面，因为平面，所以， 设点到平面的距离为，又是的中点，所以到平面的距离为因为，所以，解得，即点到平面的距离为.20．已知椭圆的左､右焦点分别为，，左顶点为A，点是椭圆C上一点，离心率为.(1)求椭圆C的方程；(2)若直线l过椭圆右焦点且与椭圆交于P､Q两点，直线AP､AQ与直线分别交于M，N.求证：M，N两点的纵坐标之积为定值；【答案】(1)(2)证明见解析 【分析】（1）根据题意，列出方程组，求得，即可求得椭圆的方程；（2）设直线的方程为，联立方程组，得到，进而求得直线的方程得到，，化简，即可证明结论成立.【详解】（1）由题意，椭圆过点，且离心率为，可得，解得，所以椭圆的方程为；（2）设直线的方程为，联立方程组，整理得，设，，可得，，直线的方程为，令，可得，同理可得，所以，M，N两点的纵坐标之积为定值.21．已知函数．(1)求的单调区间；(2)若函数恰有两个零点，求正数a的取值范围．【答案】(1)单调递减区间是，无递增区间(2) 【分析】（1），再次求导证明恒成立，从而知在定义域上的单调性；（2）分类讨论的单调性，结合极值的正负确定有两个零点满足的条件.【详解】（1）由题意可得．设，则．由，得，由，得，则在上单调递增，在上单调递减，即在上单调递增，在上单调递减，从而，故的单调递减区间是，无递增区间．（2）由题意可得．①当，即时，由，得，由，得，则在上单调递减，在上单调递增．所以要使要有两个零点，首先要求，解得．下面证明时，确实存在两个零点：所以，且,故在内存在一个零点.，因为，所以，故在内存在一个零点.所以时，存在两个零点．②当，即时，，解得，因为，所以，则有且仅有1个零点，故不符合题意．③当，即时，由，得或，由，得，则在和上单调递增，在上单调递减．显然，下面证明当时恒成立，设，则．由（1）可知在上单调递减，则，即成立.所以时不可能有两个零点．综上，恰有两个零点时正数a的取值范围是．【点睛】在解决函数零点问题时，（1）如果采取分离函数的方法，往往分离出一条直线一条曲线，或是常数和一个可讨论的函数，数形结合讨论两个函数图象交点的个数； （2）如果不分离就要分类讨论，可能要麻烦很多，要灵活运用函数的单调性、极值和零点存在性定理，数形结合寻找满足零点个数的条件.22．在直角坐标系中，直线的参数方程为（为参数）．以原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．(1)写出直线的普通方程和曲线的直角坐标方程；(2)点为曲线上一动点，求点到直线l的最大距离．【答案】(1)，(2) 【分析】（1）直接利用转换关系，在参数方程、极坐标方程和直角坐标方程之间进行转换即可解之.（2）利用圆心到直线的距离公式的应用求出结果.【详解】（1）直线的参数方程消去，可得普通方程为，即 ，曲线C的极坐标方程为，根据，转换为直角坐标方程为，即，即曲线C为圆.（2）由（1）可知，曲线C为，圆心到直线的距离为,所以点到直线l的最大距离为．