2022-2023学年青海省西宁市海湖中学高二下学期期中考试数学（文）试题含答案

这是一份2022-2023学年青海省西宁市海湖中学高二下学期期中考试数学（文）试题含答案，共12页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
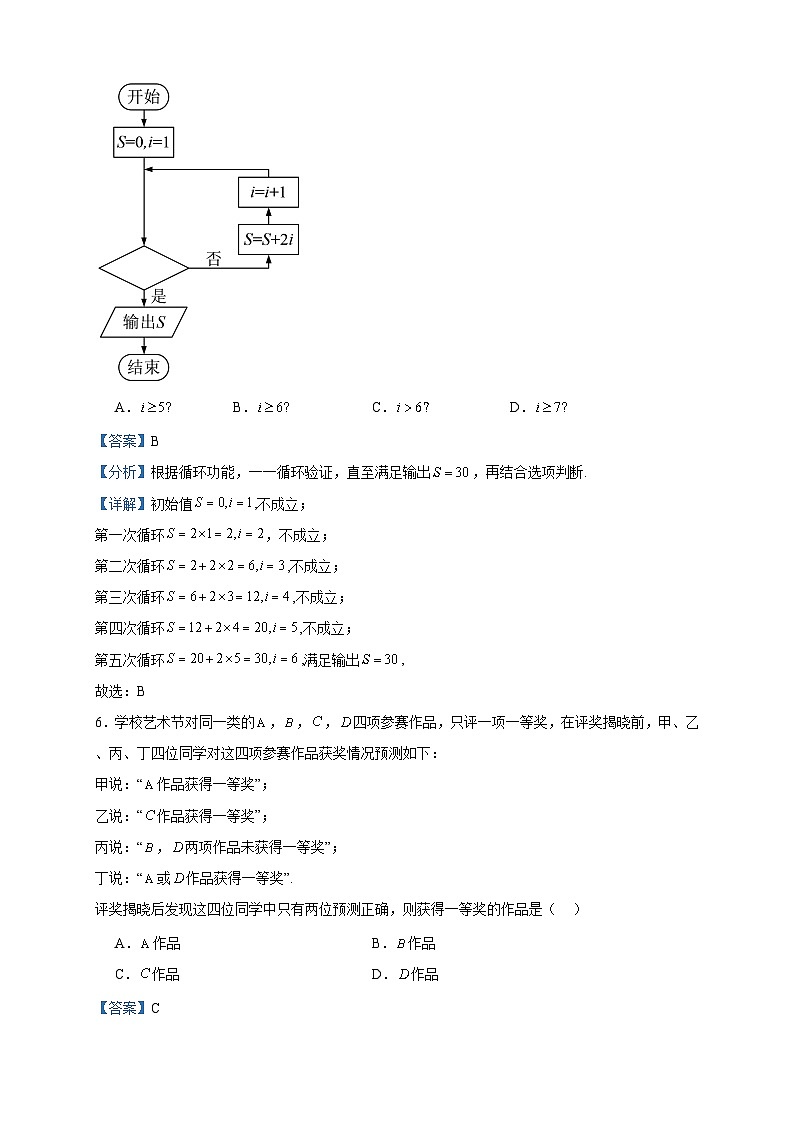
2022-2023学年青海省西宁市海湖中学高二下学期期中考试数学（文）试题 一、单选题1．在一次联考后，某校对甲、乙两个文科班的数学考试成绩进行分析，规定：大于或等于分为优秀，分以下为非优秀，统计成绩后，得到如下列联表： 优秀非优秀合计甲班人数乙班人数合计附：，其中．根据独立性检验，可以认为数学考试成绩与班级有关系的把握为（    ）A． B． C． D．【答案】D【分析】根据表格数据可得，对比临界值表可得结论.【详解】由表中的数据可得：，可以认为数学考试成绩与班级有关系的把握为．故选：D．2．下列推理过程是类比推理的为（    ）A．科学家通过研究蝙蝠的声波发明了雷达B．人们通过实验得出投骰子出现数字的概率为C．数列，，，推理出D．教室的几把椅子坏了，那么该教室内所有的椅子都坏了【答案】A【分析】根据类比推理和归纳推理定义直接判断即可.【详解】对于A，由类比推理定义知：通过研究蝙蝠的声波发明了雷达为类比推理，A正确；对于BCD，由归纳推理定义知：BCD中的推理均为归纳推理，BCD错误.故选：A.3．设复数z满足，则（    ）A． B． C． D．【答案】D【分析】先求得，然后结合复数的除法运算求得正确答案.【详解】依题意，.故选：D4．若，则（    ）A． B． C．1 D．2【答案】D【分析】利用复数的除法可求，从而可求.【详解】由题设有，故，故，故选：D 5．执行如图所示的程序框图，若输出的，则判断框中可填（    ）.A． B． C． D．【答案】B【分析】根据循环功能，一一循环验证，直至满足输出，再结合选项判断.【详解】初始值,不成立；第一次循环，不成立；第二次循环,不成立；第三次循环,不成立；第四次循环,不成立；第五次循环,满足输出,故选：B6．学校艺术节对同一类的，，，四项参赛作品，只评一项一等奖，在评奖揭晓前，甲、乙、丙、丁四位同学对这四项参赛作品获奖情况预测如下：甲说：“作品获得一等奖”；乙说：“作品获得一等奖”；丙说：“，两项作品未获得一等奖”；丁说：“或作品获得一等奖”.评奖揭晓后发现这四位同学中只有两位预测正确，则获得一等奖的作品是（    ）A．作品 B．作品C．作品 D．作品【答案】C【分析】利用获得一等奖的作品分别是A，B，C，D逐一判断预测正确的人数即可判断作答.【详解】若获得一等奖的作品是A，则甲、丙、丁预测正确，与已知矛盾，A不正确；若获得一等奖的作品是B，则甲、乙、丙、丁预测都不正确，与已知矛盾，B不正确；若获得一等奖的作品是C，则只有乙、丙预测正确，与已知相符，C正确；若获得一等奖的作品是D，则只有丁预测正确，与已知矛盾，D不正确.故选：C7．（文1）直线的参数方程为（为参数），则直线的斜率为（    ）A．3 B． C． D．【答案】D【分析】将直线的参数方程化为普通方程，从而可求得其斜率【详解】将直线的方程化为普通方程为，所以直线的斜率为，故选：D．【点睛】此题考查直线的参数方程，考查直线的斜率，属于基础题8．点的直角坐标为，则点的极坐标为（    ）A． B． C． D．【答案】C【分析】根据直角坐标与极坐标互化的原则直接转化即可.【详解】位于第四象限，与原点的距离为，且与轴所成角为，点的一个极坐标为，又，的一个极坐标为.故选：C.9．曲线（为参数）与曲线（为参数）的位置关系是（    ）A．内切 B．外切 C．相离 D．内含【答案】B【分析】将两圆的参数方程化为普通方程，再利用两圆的位置关系判断.【详解】（为参数）可化为，（为参数）可化为，圆心距为，∴两圆相外切.故选：B10．圆的圆心坐标是（    ）A． B． C． D．【答案】A【分析】将极坐标方程转化为直角坐标方程，求得圆心的直角坐标，再求得圆心的极坐标.【详解】由，得，即，所以圆心为，，点在第四象限，，所以圆心的极坐标为.故选：A11．极坐标方程表示的曲线是（    ）A．圆 B．椭圆 C．双曲线的一支 D．抛物线【答案】D【分析】利用二倍角公式和极坐标与直角坐标互化原则化简方程即可.【详解】，，即，整理可得：，表示的曲线是抛物线.故选：D.12．方程（为参数）所表示的图形是（    ）A．   B．  C．   D．  【答案】C【分析】将参数方程转化为普通方程，由此确定正确答案.【详解】，AB选项错误.，由两边平方得，即，所以C选项正确，D选项错误.故选：C 二、填空题13．已知复数，，则         【答案】/【分析】利用复数的加法运算即可得解.【详解】因为，，所以.故答案为：.14．某单位为了了解用电量y(度)与气温x(℃)之间的关系，随机统计了某4天的用电量与当天气温，并制作了对照表如下：表中数据得回归直线方程中的＝－2，预测当气温为－4℃时，用电量为        ．气温(℃)181310－1用电量(度)24343864【答案】68度【分析】先求样本数据的中心点，代入回归直线方程可得，然后代入可求.【详解】回归直线过(，)，根据题意得，，将(10，40)代入，解得＝60，，当x＝－4时，，即当气温为－4℃时用电量约为68度．【点睛】本题主要考查    回归直线方程的求解，根据回归直线一定经过样本数据的中心点可求参数，然后根据方程可求预测值，侧重考查数据分析和数学运算的核心素养.15．已知直线的极坐标方程为，则极点到该直线的距离是           .【答案】【分析】将极坐标方程化为直角坐标方程，利用点到直线距离公式可求得结果.【详解】，直线的直角坐标方程为：，即，又极点的直角坐标为，极点到该直线的距离.故答案为：.16．(坐标系与参数方程选做题)已知曲线的极坐标方程分别为则曲线与交点的极坐标为            ．【答案】【详解】本题考查极坐标方程及应用，只要直接将两方程联立求解即可；联立解方程组，解得，即两曲线的交点为． 三、解答题17．已知伸缩变换表达式为，曲线在此变换下变为椭圆，求曲线的方程.【答案】【分析】根据伸缩变换的知识求得正确答案.【详解】解因为，所以将其代入方程，得，即.故曲线C的方程为.18．实数分别为何值时，复数满足下列条件？(1)是实数.(2)是虚数.(3)是纯虚数.【答案】(1)或(2)且(3) 【分析】（1）整理题目所给复数的表达式，根据复数是实数列方程，由此求得.（2）根据复数是虚数列不等式，由此求得的范围.（3）根据复数是纯虚数列式，由此求得.【详解】（1），当，即或时，该复数为实数.（2）当，即且时，该复数为虚数.（3）当，即时，该复数为纯虚数.19．下面图形都是由小正三角形构成的,设第个图形中的黑点总数为.(1)求的值;(2)找出与的关系,并求出的表达式.①         ②           ③              ④【答案】(1)见解析；(2)【分析】（1）根据题意可直接写出结果；（2）分别计算出，，，，归纳出，再由累加法即可求出的表达式.【详解】（1）由题意可得：，，，； （2）因为； ；  ；  ；观察猜想：是一个首项为公差为的等差数列，即．因为；；；；；把上述式子累加可得到：；又因为，所以.【点睛】本题主要考查归纳推理以及累加法求数列的通项公式，属于常考题型.20．⊙O1和⊙O2的极坐标方程分别为.（Ⅰ）把⊙O1和⊙O2的极坐标方程化为直角坐标方程；（Ⅱ）求经过⊙O1，⊙O2交点的直线的直角坐标方程.【答案】（Ⅰ）为⊙O1的直角坐标方程.为⊙O2的直角坐标方程．（Ⅱ）⊙O1，⊙O2交于点（0，0）和. 过交点的直线的直角坐标方程为.【详解】以极点为原点，极轴为x轴正半轴，建立平面直角坐标系，两坐标系中取相同的长度单位.（Ⅰ），由得，所以.即为⊙O1的直角坐标方程.同理为⊙O2的直角坐标方程（Ⅱ）由解得即⊙O1，⊙O2交于点（0，0）和. 过交点的直线的直角坐标方程为.21．已知曲线的参数方程为（为参数，），直线经过且倾斜角为.（1）求曲线的普通方程；（2）直线与曲线交于，两点，求的值.【答案】（1）；（2）.【分析】（1）由曲线的参数方程消去参数，可得曲线的普通方程；（2）将直线的参数方程与曲线的普通方程进行联立，设，对应的参数分别为，,可得、的值，可得的值【详解】解：（1）由，得.代入中得，整理得曲线的普通方程为.（2）直线的参数方程为（为参数，），代入并整理得..设，对应的参数分别为，，则，，.【点睛】本题主要考查把参数方程化为普通方程的方法，及直线与圆的位置关系，考查学生的计算能力，比较基础.22．在平面直角坐标系xOy中，曲线C的参数方程为 (α为参数)，在以原点O为极点，x轴正半轴为极轴的极坐标系中，直线l的极坐标方程为ρsin＝1.（1）求C的普通方程和l的倾斜角；（2）设点P(0，)，直线l和C交于A，B两点，求|PA|＋|PB|.【答案】（1），；（2）.【分析】（1）消去参数即可求出C的普通方程，利用两角差的正弦公式，结合即可求出直线l的普通方程，进而求出倾斜角；（2）结合直线的参数方程的几何意义即可求出结果.【详解】（1）由 (α为参数)消去参数α，得，即得C的普通方程为.由，得.将代入，化简得，所以直线l的倾斜角为.（2）由（1）知，点在直线l上，可得直线l的参数方程为 (t为参数).代入并化简，得5t2＋18t＋9＝0.设两点对应的参数方程分别为t1，t2，则t1＋t2＝－＜0，t1t2＝＞0，所以|PA|＋|PB|＝|t1|＋|t2|＝－(t1＋t2)＝.